2.3.3点到直线的距离公式课件-2020-2021学年高二数学人教A版(2019)选择性必修第一册20张PPT
文档属性
| 名称 | 2.3.3点到直线的距离公式课件-2020-2021学年高二数学人教A版(2019)选择性必修第一册20张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 17:08:35 | ||
图片预览







文档简介
2.3.3点到直线的距离公式
新知导入
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 如图所示,渔民们要将船推到海里,请同学们帮助设计一下:在理论上,怎样设计能使这条路最短?
新知导入
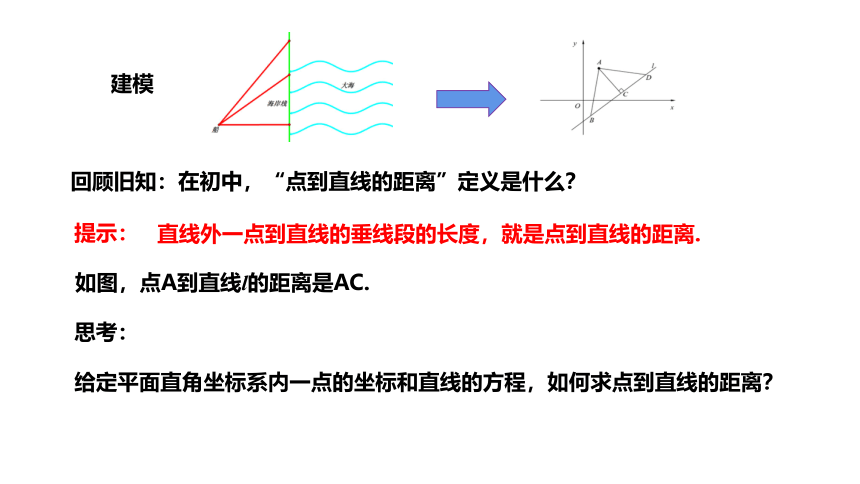
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}建模
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}回顾旧知:在初中,“点到直线的距离”定义是什么?
提示:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}直线外一点到直线的垂线段的长度,就是点到直线的距离.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图,点A到直线l的距离是AC.
思考:
给定平面直角坐标系内一点的坐标和直线的方程,如何求点到直线的距离?
新知讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知点?????????????????,??????????,直线 l :Ax + By + C=0,如何求点P到直线 l 的距离?
合作探究
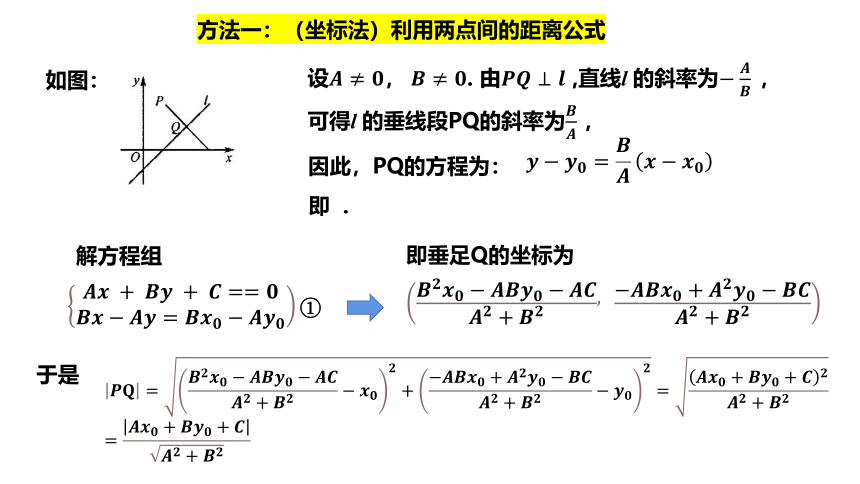
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法一:(坐标法)利用两点间的距离公式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图:
设????≠????,?????≠????. 由????????⊥???? ,直线l 的斜率为??????????,
?
可得l 的垂线段PQ的斜率为???????? ,
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因此,PQ的方程为:
?????????????=?????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}即 ?????????????????=????????????????????????? .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}解方程组
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
①
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}即垂足Q的坐标为
??????????????????????????????????????????????????+???????????????????????????+?????????????????????????????????+????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}于是
????????=??????????????????????????????????????????????????+?????????????????????+?????????????????+?????????????????????????????????+?????????????????????=????????????+????????????+????????????????+????????=????????????+????????????+????????????+?????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因此,点?????????????????,??????????到直线 l :Ax + By + C=0的距离
????=????????0+????????0+????????2+????2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}可以验证,当A=0,或B=0时,上述公式仍然成立.
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法二:用设而不求法推导
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}在上述方法中,若设垂足Q的坐标为(x, y),则
????????=?????????02+?????????02?
?
②
对于②式,你能给出它的几何意义吗?
结合方程组①
能否直接求出(?????????????)????+(?????????????)????,进而求出????????呢?
?
请你试一试!
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法二:用设而不求法推导
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
①
????????=?????????02+?????????02?
?
②
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}提示:
由方程组
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}得
&?????????????????+??????????????????=?????????????+????????????+??????????????&???????????????????????????????????=?????????????????????????????????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}将(1)(2)两边平方后相加,得
?????????+?????????????????????????+????????+?????????????????????????=????????????+????????????+?????????
?
所以
?????????????????+?????????????????=????????????+????????????+?????????????????+????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}所以
????????=?????????02+?????????02=????????0+????????0+????????2+????2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}可以验证,当A=0,或B=0时,公式仍然成立.
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法三:向量法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图,
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}点P到直线 l 的距离,就是向量????????的模.
设M(x, y)是直线 l 上的任意一点,????是与直线 l 的方向向量垂直的单位向量,则????????是????????在????上的投影向量
?
????????=?????????????
?
下面,利用直线 l 的方程得到与 l 的方向向量垂直的单位向量????.
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法三:向量法
设?????????????????,??????????,??????????????????,????????是直线
l :Ax + By + C=0上的任意两点,
?
则????????????????=(??????????????????,?????????????????)是直线 l 的方向向量.
?
????????????+????????????+????=???? , ????????????+????????????+????=???? 两式相减,
?
得 ????(?????????????????)+????(?????????????????)=???? .
?
因为,向量(A,B)与向量(??????????????????,?????????????????)垂直.
?
向量 ????????????+????????(????,????)是与直线l 的方程向量垂直的一个单位向量.
?
取 ????=????????????+????????(????,????),
?
从而,
?????????????=(??????????????,??????????????????????????+????????(????,????)=????????????+????????????(?????????????+?????????????????=????????????+????????????????+??????????????????????????????????
?
课堂练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法三:向量法
因为M(x, y)在直线 l 上,所以 Ax + By + C=0,
所以 Ax + By =-C
得
?????????????=????????????+???????????????????????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因此,
????????=????????=?????????????=????????????+????????????+????????????+?????????
?
?????????????=(??????????????,??????????????????????????+????????(????,????)=????????????+????????????????+??????????????????????????????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法四:用三角形面积公式推导
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图
????=????????????????????????
?
提示:
当A、B≠???? 时,分别作平行于x轴,y轴的两条直线,
?
分别交直线 Ax + By + C=0 于点
????(?????????????+????????,????????)
?
?????(?????????,?????????????+????????)
?
则
????????=????????+????????????+????????
?
????????=????????+?????????????+????????
?
????????=????????????+????????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}总结:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 已知一个定点?????????????????,??????????,一条直线 l :Ax +By + C=0,则定点P到这条直线 l 的距离为
????=????????????+????????????+????????????+????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①分子是P点代入直线方程;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}②分母是直线未知数x, y系数平方和的算术跟;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}③运用此公式时要注意直线方程必须是一般式,若给出其他形式,应先化成一般式再用公式;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}④当点????????在直线上时,点????????到该直线的距离为0,公式仍然适用。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}⑤直线方程 Ax +By + C=0中,A=0或B=0公式也成立。但由于直线是特殊直线(与坐标轴垂直),故也可以用数形结合求解.
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}几种特殊情况:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1. 当点????????为原点时,?????=|????|????????+????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2. 点?????????????????,??????????到x轴的距离?????=|????????|
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}3. 点?????????????????,??????????到y轴的距离?????=|????????|
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}4. 点?????????????????,??????????到与x轴平行的直线y=b(????≠????)的距离?????=|?????????????|
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}5. 点?????????????????,??????????到y轴平行的直线x=a(????≠????)的距离?????=|?????????????| .
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}例5 求点P(-1,2)到直线 l :3x=2的距离.
分析:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}将直线 l 的方程写成3x-2=0,再用点到直线的距离公式求解.
解:
点 P(-1,2)到直线 l :3x-2=0的距离
????=????×??????????????????+????????=????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}例6 已知△ABC的三个顶点分别是A(1,3),B(3,1),C(-1,0),求△ABC的面积.
分析:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}由三角形面积公式可知,只要利用距离公式求出边AB的长和边AB上的高即可.
解:
如图,
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}设边AB上的高为h ,则
????△????????????=????????????????????
?
????????=?????????????+?????????????=????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}边AB上的高h就是点C到直线AB的距离.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}边AB所在直线 l 的方程为
??????????????????=??????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}即 x+y-4=0
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}点C(-1,0)到直线 l: x+y-4=0 的距离
????=?????+?????????????????+????????=????????
?
因此,
????△????????????=????????×????????×????????=????
?
课堂练习
1. 求点P(-1,2)到下列直线的距离:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(1)2x+y-10=0; (2) x=2; (3) y-1=0.
答案:
(1) 由公式得 ?????=|????×?????+?????????????|????????+????????=????????????=????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} (2) 法1: 把直线方程化成一般式x-2=0
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}由公式得 ?????=|?????+????×?????????|????????+????????=????
法2:
∵直线 x=2与y轴平行,
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}∴由图知?????=??????????=????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(3) d=1 方法同(2)
课堂练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2. 已知点A(a,2)(a>0)到直线 l:x-y+3=0的距离为1,则a等于( )
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} A.???? B.2-???? C. ????-1 D. ????+1
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}3. 已知P(1,2),则当点P到直线2ax+y-4=0的距离最大时,a=( )
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1 B.????????? C. ???????? D. ????
解:因为直线2ax+y-4=0恒过定点A(0,4)
所以当PA与直线垂直时,点P到直线的距离达到最大值,此时过P,A的直线斜率为-2,
所以直线2ax+y-4=0的斜率为????????.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}故 ????=????????? .
C
B
课堂练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}4. 已知原点和点P(4,-1)到直线ax+a2y+6=0的距离相等,求实数a的值.
解:
利用点到直线的距离公式得
6????2+????4=|4?????????2+6|????2+????4
?
于是
????2?4?????6=±6
?
????2+????4≠0
?
且
????2?4????=0
?
????2?4????-12=0
?
或
且
????2+????4≠0
?
所以
所以????=?2或????=4或????=6
?
课堂总结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}5. 直线l: y=k(x+2) 上存在两个不同点到原点距离等于1,则k的取值范围是( )
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}A . (-2,2) B. (?????,????) C.(-1,1) D. (??????????,??????????)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}分析:将问题转化为直线l与圆????????+????????=????有两个交点,然后利用圆心到直线的距离小于半径,列式求解即可.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因为直线 l: y=k(x+2) 上存在两个不同点到原点距离等于1 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}故直线l与圆????????+????????=????有两个交点,
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}则圆心(0,0)到直线l的距离
????=2????1+????2?<1
?
解得
???????????
D
新知导入
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 如图所示,渔民们要将船推到海里,请同学们帮助设计一下:在理论上,怎样设计能使这条路最短?
新知导入
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}建模
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}回顾旧知:在初中,“点到直线的距离”定义是什么?
提示:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}直线外一点到直线的垂线段的长度,就是点到直线的距离.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图,点A到直线l的距离是AC.
思考:
给定平面直角坐标系内一点的坐标和直线的方程,如何求点到直线的距离?
新知讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知点?????????????????,??????????,直线 l :Ax + By + C=0,如何求点P到直线 l 的距离?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法一:(坐标法)利用两点间的距离公式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图:
设????≠????,?????≠????. 由????????⊥???? ,直线l 的斜率为??????????,
?
可得l 的垂线段PQ的斜率为???????? ,
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因此,PQ的方程为:
?????????????=?????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}即 ?????????????????=????????????????????????? .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}解方程组
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
①
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}即垂足Q的坐标为
??????????????????????????????????????????????????+???????????????????????????+?????????????????????????????????+????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}于是
????????=??????????????????????????????????????????????????+?????????????????????+?????????????????+?????????????????????????????????+?????????????????????=????????????+????????????+????????????????+????????=????????????+????????????+????????????+?????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因此,点?????????????????,??????????到直线 l :Ax + By + C=0的距离
????=????????0+????????0+????????2+????2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}可以验证,当A=0,或B=0时,上述公式仍然成立.
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法二:用设而不求法推导
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}在上述方法中,若设垂足Q的坐标为(x, y),则
????????=?????????02+?????????02?
?
②
对于②式,你能给出它的几何意义吗?
结合方程组①
能否直接求出(?????????????)????+(?????????????)????,进而求出????????呢?
?
请你试一试!
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法二:用设而不求法推导
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
①
????????=?????????02+?????????02?
?
②
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}提示:
由方程组
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}得
&?????????????????+??????????????????=?????????????+????????????+??????????????&???????????????????????????????????=?????????????????????????????????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}将(1)(2)两边平方后相加,得
?????????+?????????????????????????+????????+?????????????????????????=????????????+????????????+?????????
?
所以
?????????????????+?????????????????=????????????+????????????+?????????????????+????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}所以
????????=?????????02+?????????02=????????0+????????0+????????2+????2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}可以验证,当A=0,或B=0时,公式仍然成立.
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法三:向量法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图,
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}点P到直线 l 的距离,就是向量????????的模.
设M(x, y)是直线 l 上的任意一点,????是与直线 l 的方向向量垂直的单位向量,则????????是????????在????上的投影向量
?
????????=?????????????
?
下面,利用直线 l 的方程得到与 l 的方向向量垂直的单位向量????.
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法三:向量法
设?????????????????,??????????,??????????????????,????????是直线
l :Ax + By + C=0上的任意两点,
?
则????????????????=(??????????????????,?????????????????)是直线 l 的方向向量.
?
????????????+????????????+????=???? , ????????????+????????????+????=???? 两式相减,
?
得 ????(?????????????????)+????(?????????????????)=???? .
?
因为,向量(A,B)与向量(??????????????????,?????????????????)垂直.
?
向量 ????????????+????????(????,????)是与直线l 的方程向量垂直的一个单位向量.
?
取 ????=????????????+????????(????,????),
?
从而,
?????????????=(??????????????,??????????????????????????+????????(????,????)=????????????+????????????(?????????????+?????????????????=????????????+????????????????+??????????????????????????????????
?
课堂练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法三:向量法
因为M(x, y)在直线 l 上,所以 Ax + By + C=0,
所以 Ax + By =-C
得
?????????????=????????????+???????????????????????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因此,
????????=????????=?????????????=????????????+????????????+????????????+?????????
?
?????????????=(??????????????,??????????????????????????+????????(????,????)=????????????+????????????????+??????????????????????????????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法四:用三角形面积公式推导
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}如图
????=????????????????????????
?
提示:
当A、B≠???? 时,分别作平行于x轴,y轴的两条直线,
?
分别交直线 Ax + By + C=0 于点
????(?????????????+????????,????????)
?
?????(?????????,?????????????+????????)
?
则
????????=????????+????????????+????????
?
????????=????????+?????????????+????????
?
????????=????????????+????????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}总结:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 已知一个定点?????????????????,??????????,一条直线 l :Ax +By + C=0,则定点P到这条直线 l 的距离为
????=????????????+????????????+????????????+????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①分子是P点代入直线方程;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}②分母是直线未知数x, y系数平方和的算术跟;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}③运用此公式时要注意直线方程必须是一般式,若给出其他形式,应先化成一般式再用公式;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}④当点????????在直线上时,点????????到该直线的距离为0,公式仍然适用。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}⑤直线方程 Ax +By + C=0中,A=0或B=0公式也成立。但由于直线是特殊直线(与坐标轴垂直),故也可以用数形结合求解.
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}几种特殊情况:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1. 当点????????为原点时,?????=|????|????????+????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2. 点?????????????????,??????????到x轴的距离?????=|????????|
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}3. 点?????????????????,??????????到y轴的距离?????=|????????|
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}4. 点?????????????????,??????????到与x轴平行的直线y=b(????≠????)的距离?????=|?????????????|
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}5. 点?????????????????,??????????到y轴平行的直线x=a(????≠????)的距离?????=|?????????????| .
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}例5 求点P(-1,2)到直线 l :3x=2的距离.
分析:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}将直线 l 的方程写成3x-2=0,再用点到直线的距离公式求解.
解:
点 P(-1,2)到直线 l :3x-2=0的距离
????=????×??????????????????+????????=????????
?
合作探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}例6 已知△ABC的三个顶点分别是A(1,3),B(3,1),C(-1,0),求△ABC的面积.
分析:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}由三角形面积公式可知,只要利用距离公式求出边AB的长和边AB上的高即可.
解:
如图,
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}设边AB上的高为h ,则
????△????????????=????????????????????
?
????????=?????????????+?????????????=????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}边AB上的高h就是点C到直线AB的距离.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}边AB所在直线 l 的方程为
??????????????????=??????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}即 x+y-4=0
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}点C(-1,0)到直线 l: x+y-4=0 的距离
????=?????+?????????????????+????????=????????
?
因此,
????△????????????=????????×????????×????????=????
?
课堂练习
1. 求点P(-1,2)到下列直线的距离:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(1)2x+y-10=0; (2) x=2; (3) y-1=0.
答案:
(1) 由公式得 ?????=|????×?????+?????????????|????????+????????=????????????=????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} (2) 法1: 把直线方程化成一般式x-2=0
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}由公式得 ?????=|?????+????×?????????|????????+????????=????
法2:
∵直线 x=2与y轴平行,
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}∴由图知?????=??????????=????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(3) d=1 方法同(2)
课堂练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2. 已知点A(a,2)(a>0)到直线 l:x-y+3=0的距离为1,则a等于( )
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} A.???? B.2-???? C. ????-1 D. ????+1
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}3. 已知P(1,2),则当点P到直线2ax+y-4=0的距离最大时,a=( )
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1 B.????????? C. ???????? D. ????
解:因为直线2ax+y-4=0恒过定点A(0,4)
所以当PA与直线垂直时,点P到直线的距离达到最大值,此时过P,A的直线斜率为-2,
所以直线2ax+y-4=0的斜率为????????.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}故 ????=????????? .
C
B
课堂练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}4. 已知原点和点P(4,-1)到直线ax+a2y+6=0的距离相等,求实数a的值.
解:
利用点到直线的距离公式得
6????2+????4=|4?????????2+6|????2+????4
?
于是
????2?4?????6=±6
?
????2+????4≠0
?
且
????2?4????=0
?
????2?4????-12=0
?
或
且
????2+????4≠0
?
所以
所以????=?2或????=4或????=6
?
课堂总结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}5. 直线l: y=k(x+2) 上存在两个不同点到原点距离等于1,则k的取值范围是( )
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}A . (-2,2) B. (?????,????) C.(-1,1) D. (??????????,??????????)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}分析:将问题转化为直线l与圆????????+????????=????有两个交点,然后利用圆心到直线的距离小于半径,列式求解即可.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因为直线 l: y=k(x+2) 上存在两个不同点到原点距离等于1 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}故直线l与圆????????+????????=????有两个交点,
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}则圆心(0,0)到直线l的距离
????=2????1+????2?<1
?
解得
???????????
D
