9.2.1、9.2.2 总体取值规律的估计 总体百分位数的估计课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册(共17张PPT)
文档属性
| 名称 | 9.2.1、9.2.2 总体取值规律的估计 总体百分位数的估计课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 19:34:53 | ||
图片预览






文档简介
(共17张PPT)
9.2.1、9.2.2
总体取值规律的估计
总体百分位数的估计
一、回顾
上节课学习了获取数据的途径,共有4个分别为:
1、通过调查获取数据:
2、通过试验获取数据
3、通过观察获取数据
4、通过查询获得数据
实际问题中数据多而且杂乱,往往无法直接从原始数据中发现规律,所以需要根据问题的背景特点,选择合适统计图表对数据进行整理和直观描述.
学习目标:
1.会列频率分布表,会画频率分布直方图,理解它们的特点.
2.会画条形图,扇形图,折线图等统计图,理解它们的特点.
3.会用样本的频率分布估计总体分布.
一、导入
思考1、
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.
某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费,如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
一、导入
每户居民月均用水量标准如果定得太低,会影响很多居民的日常生活;如果标准太高,则不利于节水、为了确定一个较为合理的用水标准,必须先了解在全市所有居民用户中,月用水量在不同范围内的居民用户所占的比例情况.
由于全市居民用户很多,所以采用抽样调查的方式,通过分析样本观测数据,来估计全市居民用户的月均用水量
在这个问题中,总体是该市的全体居民用户,个体是每户居民用户,调查的变量是居民用户的月均用水量
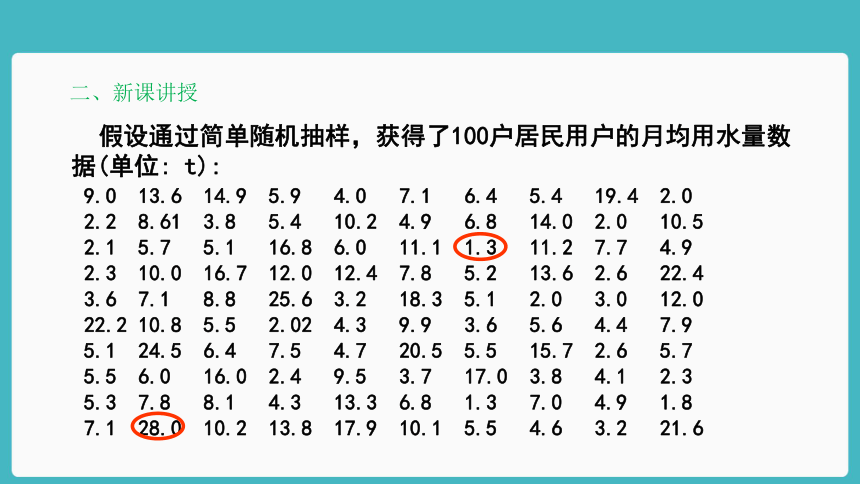
二、新课讲授
假设通过简单随机抽样,获得了100户居民用户的月均用水量数据(单位:
t):
9.0
13.6
14.9
5.9
4.0
7.1
6.4
5.4
19.4
2.0
2.2
8.61
3.8
5.4
10.2
4.9
6.8
14.0
2.0
10.5
2.1
5.7
5.1
16.8
6.0
11.1
1.3
11.2
7.7
4.9
2.3
10.0
16.7
12.0
12.4
7.8
5.2
13.6
2.6
22.4
3.6
7.1
8.8
25.6
3.2
18.3
5.1
2.0
3.0
12.0
22.2
10.8
5.5
2.02
4.3
9.9
3.6
5.6
4.4
7.9
5.1
24.5
6.4
7.5
4.7
20.5
5.5
15.7
2.6
5.7
5.5
6.0
16.0
2.4
9.5
3.7
17.0
3.8
4.1
2.3
5.3
7.8
8.1
4.3
13.3
6.8
1.3
7.0
4.9
1.8
7.1
28.0
10.2
13.8
17.9
10.1
5.5
4.6
3.2
21.6
将一批数据按要求分为若干组,各组内的数据的个数,叫做该组数据的频数,各个小组数据在样本容量中所占的比例的大小,叫做该组数据的频率。
为了解数据分布的规律,可利用频率分布表和频率分布图来分析,具体做法如下:
1、求极差(即一组数据中最大值和最小值的差)
例如,
28-1.3=26.7,
这说明这些数据的变化范围大小是26.7t。
2、决定组距和组数
例如,若取组距为3,则
故可将数据分成9组。
分组
频数
频率
[1.2,4.2)
23
0.23
[4.2,7.2)
32
0.32
[7.2,10.2)
13
0.13
[10.2,13.2)
9
0.09
[13.2,16.2)
9
0.09
[16.2,19.2)
5
0.05
[19.2,22.2)
3
0.03
[22.2,25.2)
4
0.04
[25.2,28.2]
2
0.02
合计
100
1.00
4、列频率分布表:
3、将数据分组:
以组距3将数据分组如下:
[1.2,4.2),
[4.2,7.2),……,[25.2,28.2
]
5、画频率分布直方图
用横轴表示月均用水量,纵轴表示频率与组距的比值,以每个组距为底,以频率除以组距的商为高,分别画出矩形,这样得到的直方图就是频率分布直方图。
思考:小矩形的面积与哪些量有关?如何表示?
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
所有小长方形的面积之和=1
注:
1、横轴表示月均用水量,纵轴表示:
。
频率
组距
这里,
实际上就是频率分布直方图中各小长方
形的高度,它反映了各组样本观测数据的疏密程度。
频率
组距
2、小长方形的面积=组距
×
=频率。
频率
组距
所以各小长方形的面积表示相应各组的频率。各小长方形的面积的总和等于1.
1).求极差(即一组数据中最大值与最小值的差)
2).决定组距与组数(将数据分组)
3).
将数据分组
方法小结:画频率分布直方图的步骤
4).列出频率分布表.(填写频率/组距一栏)
5).画出频率分布直方图.
组距:指每个小组的两个端点的距离,
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组.
例1
已知某市2015年全年空气质量等级如下表所示.
空气质量等级(空气质量指数(AQD)
频数
频率
优(AQI≤50)
83
22.8%
良(50121
33.2%
轻度污染(10068
18.6%
中度污染(15049
13.4%
重度污染(20030
8.2%
严重污染(AQI>300)
14
3.8%
合计
365
100%
2016年5月和6月的空气质量指数如下:
5月:240
80
56
53
92
126
45
87
56
60
191
62
55
58
56
53
89
90
125
124
103
81
89
44
34
53
79
81
62
116
88
6月:63
92
110
122
102
116
81
163
158
76
33
102
65
53
38
55
52
76
99
127
120
80
108
33
35
73
82
90
146
95
选择合适的统计图描述数据,并回答下列问题:
(1)分析该市2016年6月的空气质量情况.
(2)该市2016年5月和6月的空气质量,哪个月较好?
(3)比较该市2016年6月与该市2015年全年的空气质量,2016年6月的空气质量是否好于去年?
练一练
1.某学校在全体高一学生中随机抽查部分学生,了解学生的上学方式学生的上学方式主要有:A骑自行车,B步行,C乘公交车,D其他将收集的数据整理、绘制成两幅不完整的统计图,如图.请根据图中信息,估计骑自行车的学生人数占高一学生总人数的百分比是(
)
C
A.36.25%
B.40%
C.41.25%
D.56.25%
练一练
练一练
2.某商家统计了去年P,Q两种产品的月销售额(单位:万元),绘制了月销售额的雷达图,图中A点表示P产品2月份销售额约为20万元,B点表示Q产品9月份销售额约为25万元.
根据图中信息,下面统计结论错误的是(
)
A.P产品销售额的极差较大
B.P产品销售额的中位数较大
C.Q产品销售额的平均值较大
D.Q产品销售额的波动较小
B
1.不同的统计图在表示数据上有不同的特点
①扇形图主要用于直观描述各类数据占总数的比例;
②条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率;
③折线图主要用于描述数据随时间的变化趋势.
2.不同的统计图适用的数据类型不同
①条形图适用于描述离散型的数据;
②直方图适用描述连续型数据,
再见
“
”
9.2.1、9.2.2
总体取值规律的估计
总体百分位数的估计
一、回顾
上节课学习了获取数据的途径,共有4个分别为:
1、通过调查获取数据:
2、通过试验获取数据
3、通过观察获取数据
4、通过查询获得数据
实际问题中数据多而且杂乱,往往无法直接从原始数据中发现规律,所以需要根据问题的背景特点,选择合适统计图表对数据进行整理和直观描述.
学习目标:
1.会列频率分布表,会画频率分布直方图,理解它们的特点.
2.会画条形图,扇形图,折线图等统计图,理解它们的特点.
3.会用样本的频率分布估计总体分布.
一、导入
思考1、
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.
某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费,如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
一、导入
每户居民月均用水量标准如果定得太低,会影响很多居民的日常生活;如果标准太高,则不利于节水、为了确定一个较为合理的用水标准,必须先了解在全市所有居民用户中,月用水量在不同范围内的居民用户所占的比例情况.
由于全市居民用户很多,所以采用抽样调查的方式,通过分析样本观测数据,来估计全市居民用户的月均用水量
在这个问题中,总体是该市的全体居民用户,个体是每户居民用户,调查的变量是居民用户的月均用水量
二、新课讲授
假设通过简单随机抽样,获得了100户居民用户的月均用水量数据(单位:
t):
9.0
13.6
14.9
5.9
4.0
7.1
6.4
5.4
19.4
2.0
2.2
8.61
3.8
5.4
10.2
4.9
6.8
14.0
2.0
10.5
2.1
5.7
5.1
16.8
6.0
11.1
1.3
11.2
7.7
4.9
2.3
10.0
16.7
12.0
12.4
7.8
5.2
13.6
2.6
22.4
3.6
7.1
8.8
25.6
3.2
18.3
5.1
2.0
3.0
12.0
22.2
10.8
5.5
2.02
4.3
9.9
3.6
5.6
4.4
7.9
5.1
24.5
6.4
7.5
4.7
20.5
5.5
15.7
2.6
5.7
5.5
6.0
16.0
2.4
9.5
3.7
17.0
3.8
4.1
2.3
5.3
7.8
8.1
4.3
13.3
6.8
1.3
7.0
4.9
1.8
7.1
28.0
10.2
13.8
17.9
10.1
5.5
4.6
3.2
21.6
将一批数据按要求分为若干组,各组内的数据的个数,叫做该组数据的频数,各个小组数据在样本容量中所占的比例的大小,叫做该组数据的频率。
为了解数据分布的规律,可利用频率分布表和频率分布图来分析,具体做法如下:
1、求极差(即一组数据中最大值和最小值的差)
例如,
28-1.3=26.7,
这说明这些数据的变化范围大小是26.7t。
2、决定组距和组数
例如,若取组距为3,则
故可将数据分成9组。
分组
频数
频率
[1.2,4.2)
23
0.23
[4.2,7.2)
32
0.32
[7.2,10.2)
13
0.13
[10.2,13.2)
9
0.09
[13.2,16.2)
9
0.09
[16.2,19.2)
5
0.05
[19.2,22.2)
3
0.03
[22.2,25.2)
4
0.04
[25.2,28.2]
2
0.02
合计
100
1.00
4、列频率分布表:
3、将数据分组:
以组距3将数据分组如下:
[1.2,4.2),
[4.2,7.2),……,[25.2,28.2
]
5、画频率分布直方图
用横轴表示月均用水量,纵轴表示频率与组距的比值,以每个组距为底,以频率除以组距的商为高,分别画出矩形,这样得到的直方图就是频率分布直方图。
思考:小矩形的面积与哪些量有关?如何表示?
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
所有小长方形的面积之和=1
注:
1、横轴表示月均用水量,纵轴表示:
。
频率
组距
这里,
实际上就是频率分布直方图中各小长方
形的高度,它反映了各组样本观测数据的疏密程度。
频率
组距
2、小长方形的面积=组距
×
=频率。
频率
组距
所以各小长方形的面积表示相应各组的频率。各小长方形的面积的总和等于1.
1).求极差(即一组数据中最大值与最小值的差)
2).决定组距与组数(将数据分组)
3).
将数据分组
方法小结:画频率分布直方图的步骤
4).列出频率分布表.(填写频率/组距一栏)
5).画出频率分布直方图.
组距:指每个小组的两个端点的距离,
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组.
例1
已知某市2015年全年空气质量等级如下表所示.
空气质量等级(空气质量指数(AQD)
频数
频率
优(AQI≤50)
83
22.8%
良(50
33.2%
轻度污染(100
18.6%
中度污染(150
13.4%
重度污染(200
8.2%
严重污染(AQI>300)
14
3.8%
合计
365
100%
2016年5月和6月的空气质量指数如下:
5月:240
80
56
53
92
126
45
87
56
60
191
62
55
58
56
53
89
90
125
124
103
81
89
44
34
53
79
81
62
116
88
6月:63
92
110
122
102
116
81
163
158
76
33
102
65
53
38
55
52
76
99
127
120
80
108
33
35
73
82
90
146
95
选择合适的统计图描述数据,并回答下列问题:
(1)分析该市2016年6月的空气质量情况.
(2)该市2016年5月和6月的空气质量,哪个月较好?
(3)比较该市2016年6月与该市2015年全年的空气质量,2016年6月的空气质量是否好于去年?
练一练
1.某学校在全体高一学生中随机抽查部分学生,了解学生的上学方式学生的上学方式主要有:A骑自行车,B步行,C乘公交车,D其他将收集的数据整理、绘制成两幅不完整的统计图,如图.请根据图中信息,估计骑自行车的学生人数占高一学生总人数的百分比是(
)
C
A.36.25%
B.40%
C.41.25%
D.56.25%
练一练
练一练
2.某商家统计了去年P,Q两种产品的月销售额(单位:万元),绘制了月销售额的雷达图,图中A点表示P产品2月份销售额约为20万元,B点表示Q产品9月份销售额约为25万元.
根据图中信息,下面统计结论错误的是(
)
A.P产品销售额的极差较大
B.P产品销售额的中位数较大
C.Q产品销售额的平均值较大
D.Q产品销售额的波动较小
B
1.不同的统计图在表示数据上有不同的特点
①扇形图主要用于直观描述各类数据占总数的比例;
②条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率;
③折线图主要用于描述数据随时间的变化趋势.
2.不同的统计图适用的数据类型不同
①条形图适用于描述离散型的数据;
②直方图适用描述连续型数据,
再见
“
”
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
