4.5 函数的应用(二) 同步练习- 2021-2022学年高一上学期数学必刷题(人教A版2019必修第一册)(Word版含解析)
文档属性
| 名称 | 4.5 函数的应用(二) 同步练习- 2021-2022学年高一上学期数学必刷题(人教A版2019必修第一册)(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 551.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 21:14:59 | ||
图片预览




文档简介
2021-2022学年高一数学经典题型必刷(人教A版2019必修第一册))
第4.5课时
函数的应用(二)
一、单选题(本大题共8小题,每小题只有一个选项符合题意)
1.已知甲、乙两种商品在过去一段时间内的价格走势如图所示.假设某商人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计).如果他在t4时刻卖出所有商品,那么他将获得的最大利润是(
)
A.40万元
B.60万元
C.80万元
D.120万元
2.某地区植被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷?0.4万公顷和0.76万公顷,则沙漠增加值y(万公顷)关于年数x(年)的函数关系较为近似的是(
)
A.y=0.2x
B.
C.y=x2+2x
D.
3.若是二次函数的两个零点,则的值为(
)
A.
B.
C.
D.
4.方程只有一个实数解,则实数m的取值范围是(
)
A.
B.
C.
D.或
5.在某种新型材料的研制中,试验人员获得了下列一组试验数据.现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是(
)
x
1.95
3.00
3.94
5.10
6.12
y
0.97
1.59
1.98
2.35
2.61
A.y=2x
B.y=log2x
C.y=(x2-1)
D.y=2.61x
6.当x越来越大时,下列函数中增长速度最快的是(
)
A.
B.
C.
D.
7.若函数经过点,则函数的零点是(
)
A.0,2
B.0,
C.0,
D.2,
8.下面是一幅统计图,根据此图得到的以下说法中,正确的个数是(
)
①这几年生活水平逐年得到提高;
②生活费收入指数增长最快的一年是2014年;
③生活价格指数上涨速度最快的一年是2015年;
④虽然2016年生活费收入增长缓慢,但生活价格指数也略有降低,因而生活水平有较大的改善.
A.1
B.2
C.3
D.4
二、多选题(本大题共4小题,每小题有两项或以上符合题意)
9.已知每生产100克饼干的原材料加工费为1.8元,某食品加工厂对饼干采用两种包装,其包装费用、销售价格如表所示:
型号
小包装
大包装
质量
100克
300克
包装费
0.5元
0.7元
销售价格
3.00元
8.4元
则下列说法正确的是(
)
A.买小包装实惠
B.买大包装实惠
C.卖3小包比卖1大包盈利多
D.卖1大包比卖3小包盈利多
10.已知函数若函数恰有2个零点,则实数m可以是(
)
A.
B.0
C.1
D.2
11.(多选)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费,甲厂的总费用y1(千元)?乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲?乙所示,则(
)
A.甲厂的制版费为1千元,印刷费平均每个为0.5元
B.甲厂的总费用y1与证书数量x之间的函数关系式为
C.当印制证书数量不超过2千个时,乙厂的印刷费平均每个为1.5元
D.当印制证书数量超过2千个时,乙厂的总费用y2与证书数量x之间的函数关系式为
12.已知函数,若x1)
A.x1+x2=-1
B.x3x4=1
C.1D.0三、填空题(本大题共4小题)
13.用二分法求方程在区间[2,3]内的实根,由计算器可算得,,,那么下一个有根区间为_________.
14.若方程的根在内,则的取值范围是_____.
15.某商人将彩电先按原价提高40%,然后在广告上写上“大酬宾,八折优惠”,结果是每台彩电比原价多赚了270元,则每台彩电的原价为________元.
16.函数在区间和内各有一个零点,则实数的取值范围是___________.
四、解答题(本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程)
17.已知关于的方程,求方程实数根的个数?
18.某公司为了实现2019年销售利润1000万元的目标,准备制定一个激励销售人员的奖励方案:从销售利润达到10万元开始,按销售利润进行奖励,且奖金数额y(万元)随销售利润x(万元)的增加而增加,但奖金数额不超过5万元.现有三个奖励模型:y=0.025x,y=1.003x,y=lnx+1,其中是否有模型能完全符合公司的要求?请说明理由.(参考数据:1.003538≈5,e≈2.71828…,e8≈2981)
19.已知二次函数.
(1)若二次函数有零点,求实数的取值范围;
(2)如果是满足(1)的最大整数,且二次函数的零点是二次函数的一个零点,求的值及二次函数的另一个零点.
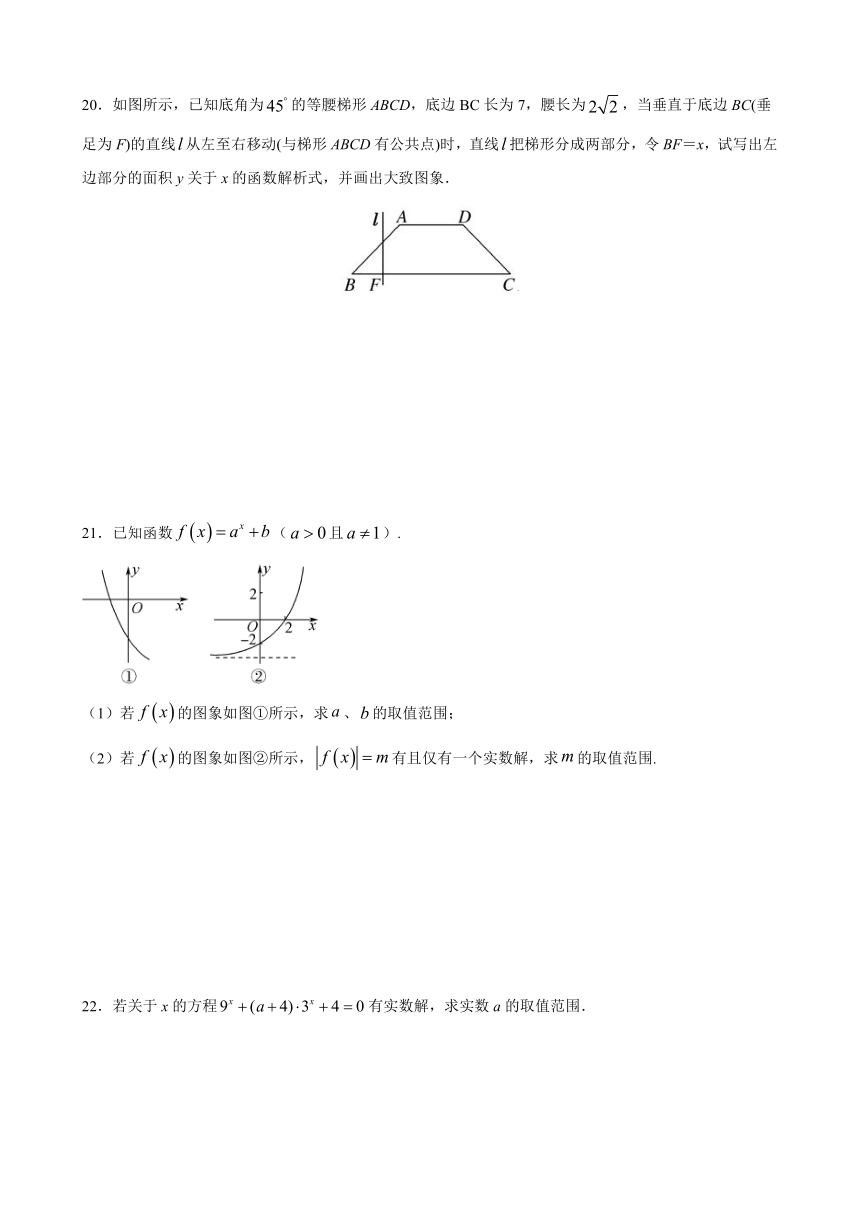
20.如图所示,已知底角为的等腰梯形ABCD,底边BC长为7,腰长为,当垂直于底边BC(垂足为F)的直线从左至右移动(与梯形ABCD有公共点)时,直线把梯形分成两部分,令BF=x,试写出左边部分的面积y关于x的函数解析式,并画出大致图象.
21.已知函数(且).
(1)若的图象如图①所示,求、的取值范围;
(2)若的图象如图②所示,有且仅有一个实数解,求的取值范围.
22.若关于x的方程有实数解,求实数a的取值范围.
参考答案
1.D
【解析】甲6元时,该商人全部买入甲商品,可以买120÷6=20(万份),在t2时刻全部卖出,此时获利20×2=40(万元),
乙4元时,该商人买入乙商品,可以买(120+40)÷4=40(万份),在t4时刻全部卖出,此时获利40×2=80(万元),共获利40+80=120(万元).
故选:D
2.B
【解析】由题意得图像上三点:,
对于A选项:y=0.2x,将三点代入y=0.2x,
当时,函数值与0.76相差较大;
对于B选项:,将三点代入,
当时,函数值与0.76相差仅有0.04;
对于C选项:y=x2+2x,将三点代入y=x2+2x,
当时,函数值都与实际数值相差较大;
对于D选项:,将三点代入,
当时,函数值都与0.76相差较大;
综上:沙漠增加值y(万公顷)关于年数x(年)的函数关系较为近似的是.
故选:B.
3.D
【解析】由题意,令,解得或,
不妨设,代入可得.
故选:D.
4.D
【解析】令,则方程只有一个正根,
当方程有唯一根时,则,此时根为符合题意;
当方程有一正一负根或一正根和0根时,有,则.
综上所述,或
故选:D
5.B
【解析】对于A,函数是指数函数,增长速度很快,且在时,时,代入值偏差较大,不符合要求;
对于B,函数,是对数函数,增长速度缓慢,且在时,时,基本符合要求;
对于C,函数是二次函数,且当时,时,代入值偏差较大,不符合要求;
对于D,函数,当时,不符合要求,
故选:B.
6.B
【解析】因为指数函数是几何级数增长,当x越来越大时,增长速度最快.
故选:B.
7.C
【解析】函数经过点,,∴,
∴,
令,则
所以函数的零点是0和.
故选:C.
8.C
【解析】由图知,“生活费收入指数”减去“生活价格指数”的差是逐年增大的,故①正确;
“生活费收入指数”在2014~2015年最陡;故②正确;
“生活价格指数”在2015~2016年最平缓,故③不正确;
“生活价格指数”略呈下降,而“生活费收入指数”呈上升趋势,故④正确.
故选:C.
9.BD
【解析】大包装300克8.4元,则等价为100克2.8元,小包装100克3元,则买大包装实惠,故B正确,
卖1大包的盈利8.4-0.7-1.8×3=2.3(元),卖1小包盈利3-0.5-1.8=0.7(元),则卖3小包盈利0.7×3=2.1(元),则卖1大包比卖3小包盈利多,故D正确.
故选:BD
10.ABC
【解析】因为函数恰有2个零点,
所以函数的图象与直线恰有两个交点,
画出函数的图象如图:
由图可知,或,结合选项,因此可以为-1,0,1.
故选:ABC.
11.ABCD
【解析】由题图知甲厂制版费为1千元,印刷费平均每个为0.5元,故A正确;
设甲厂的费用与证书数量满足的函数关系式为,
代入点,可得,解得,
所以甲厂的费用与证书数量满足的函数关系式为,故B正确;
当印制证书数量不超过2千个时,乙厂的印刷费平均每个为元,故C正确;
设当时,设与之间的函数关系式为
代入点,可得,解得,
所以当时,与之间的函数关系式为,故D正确.
故选:ABCD.
12.BCD
【解析】由函数解析式可得图象如下:
∴由图知:,,而当时,有,即或2,
∴,而知:,
∴,.
故选:BCD
13.
【解析】,,,
所以下一个有根区间为.
故答案为:
14.
【解析】设,则,解得:,
即的取值范围为.
故答案为:.
15.2250
【解析】设彩电的原价为a元,∴a(1+40%)·80%-a=270,∴0.12a=270,解得a=2
250.
∴每台彩电的原价为2
250元.
故答案为:2250.
16.
【解析】为开口方向向上,对称轴为的二次函数,
,即,解得:,即实数的取值范围为.
故答案为:.
17.答案见解析
【解析】作出函数的图象如图所示,
当或时,方程实数根有两个.
当时,方程实数根有三个.
当时,方程实数根有四个.
当时,方程无实数根.
18.奖励模型能完全符合公司的要求,答案见解析.
【解析】解:由题意,符合公司要求的模型需同时满足:
当x∈[10,1000]时,①函数为增函数;②函数的最大值不超过5;③y≤x·25%.
(1)对于y=0.025x,易知满足①,但当x>200时,y>5,不满足公司的要求;
(2)对于y=1.003x,易知满足①,但当x>538时,不满足公司的要求;
(3)对于,易知满足①.
当x∈[10,1000]时,y≤ln1000+1.
下面证明ln1000+1<5.
因为ln1000+1-5=ln1000-4=
(ln1000-8)=(ln1000-ln2981)<0,满足②.
再证明lnx+1≤x·25%,即2lnx+4-x≤0.
设F(x)=2lnx+4-x,则F′(x)=
-1=<0,x∈[10,1000],
所以F(x)在[10,1000]上为减函数,
F(x)max=F(10)=2ln10+4-10=2ln10-6=2(ln10-3)<0,满足③.
综上,奖励模型能完全符合公司的要求.
19.(1);(2),另一个零点为4.
【解析】(1)由题意得,所以,解得.
(2)由(1)可知,
所以方程的根,二次函数的零点是,
∴二次函数的一个零点是,
∴方程的一个根为2,
∴,解得,
∴,解得或,
所以二次函数的另一个零点为4.
20.,图见解析.
【解析】如图,过点A,D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.
因为四边形ABCD是等腰梯形,底角为45°,,所以BG=AG=DH=HC=2.
又BC=7,所以AD=GH=3.
当点F在BG上,即x∈[0,2]时,;
当点F在GH(不包括点G)上,即x∈(2,5]时,;
当点F在HC(不包括点H)上,即x∈(5,7]时,.
综上,得左边部分的面积y关于x的函数解析式为,
其大致图象如图所示.
21.(1),;(2)或.
【解析】(1)由为减函数可得,又,解得;
(2)图②中
,函数的图象如图所示.
由图象可知使有且仅有一解,则或.
22.
【解析】令,则原方程等价为有正根,又,
知此方程有两个正根,则应满足,
即,解得.
第4.5课时
函数的应用(二)
一、单选题(本大题共8小题,每小题只有一个选项符合题意)
1.已知甲、乙两种商品在过去一段时间内的价格走势如图所示.假设某商人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计).如果他在t4时刻卖出所有商品,那么他将获得的最大利润是(
)
A.40万元
B.60万元
C.80万元
D.120万元
2.某地区植被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷?0.4万公顷和0.76万公顷,则沙漠增加值y(万公顷)关于年数x(年)的函数关系较为近似的是(
)
A.y=0.2x
B.
C.y=x2+2x
D.
3.若是二次函数的两个零点,则的值为(
)
A.
B.
C.
D.
4.方程只有一个实数解,则实数m的取值范围是(
)
A.
B.
C.
D.或
5.在某种新型材料的研制中,试验人员获得了下列一组试验数据.现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是(
)
x
1.95
3.00
3.94
5.10
6.12
y
0.97
1.59
1.98
2.35
2.61
A.y=2x
B.y=log2x
C.y=(x2-1)
D.y=2.61x
6.当x越来越大时,下列函数中增长速度最快的是(
)
A.
B.
C.
D.
7.若函数经过点,则函数的零点是(
)
A.0,2
B.0,
C.0,
D.2,
8.下面是一幅统计图,根据此图得到的以下说法中,正确的个数是(
)
①这几年生活水平逐年得到提高;
②生活费收入指数增长最快的一年是2014年;
③生活价格指数上涨速度最快的一年是2015年;
④虽然2016年生活费收入增长缓慢,但生活价格指数也略有降低,因而生活水平有较大的改善.
A.1
B.2
C.3
D.4
二、多选题(本大题共4小题,每小题有两项或以上符合题意)
9.已知每生产100克饼干的原材料加工费为1.8元,某食品加工厂对饼干采用两种包装,其包装费用、销售价格如表所示:
型号
小包装
大包装
质量
100克
300克
包装费
0.5元
0.7元
销售价格
3.00元
8.4元
则下列说法正确的是(
)
A.买小包装实惠
B.买大包装实惠
C.卖3小包比卖1大包盈利多
D.卖1大包比卖3小包盈利多
10.已知函数若函数恰有2个零点,则实数m可以是(
)
A.
B.0
C.1
D.2
11.(多选)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费,甲厂的总费用y1(千元)?乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲?乙所示,则(
)
A.甲厂的制版费为1千元,印刷费平均每个为0.5元
B.甲厂的总费用y1与证书数量x之间的函数关系式为
C.当印制证书数量不超过2千个时,乙厂的印刷费平均每个为1.5元
D.当印制证书数量超过2千个时,乙厂的总费用y2与证书数量x之间的函数关系式为
12.已知函数,若x1
A.x1+x2=-1
B.x3x4=1
C.1
13.用二分法求方程在区间[2,3]内的实根,由计算器可算得,,,那么下一个有根区间为_________.
14.若方程的根在内,则的取值范围是_____.
15.某商人将彩电先按原价提高40%,然后在广告上写上“大酬宾,八折优惠”,结果是每台彩电比原价多赚了270元,则每台彩电的原价为________元.
16.函数在区间和内各有一个零点,则实数的取值范围是___________.
四、解答题(本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程)
17.已知关于的方程,求方程实数根的个数?
18.某公司为了实现2019年销售利润1000万元的目标,准备制定一个激励销售人员的奖励方案:从销售利润达到10万元开始,按销售利润进行奖励,且奖金数额y(万元)随销售利润x(万元)的增加而增加,但奖金数额不超过5万元.现有三个奖励模型:y=0.025x,y=1.003x,y=lnx+1,其中是否有模型能完全符合公司的要求?请说明理由.(参考数据:1.003538≈5,e≈2.71828…,e8≈2981)
19.已知二次函数.
(1)若二次函数有零点,求实数的取值范围;
(2)如果是满足(1)的最大整数,且二次函数的零点是二次函数的一个零点,求的值及二次函数的另一个零点.
20.如图所示,已知底角为的等腰梯形ABCD,底边BC长为7,腰长为,当垂直于底边BC(垂足为F)的直线从左至右移动(与梯形ABCD有公共点)时,直线把梯形分成两部分,令BF=x,试写出左边部分的面积y关于x的函数解析式,并画出大致图象.
21.已知函数(且).
(1)若的图象如图①所示,求、的取值范围;
(2)若的图象如图②所示,有且仅有一个实数解,求的取值范围.
22.若关于x的方程有实数解,求实数a的取值范围.
参考答案
1.D
【解析】甲6元时,该商人全部买入甲商品,可以买120÷6=20(万份),在t2时刻全部卖出,此时获利20×2=40(万元),
乙4元时,该商人买入乙商品,可以买(120+40)÷4=40(万份),在t4时刻全部卖出,此时获利40×2=80(万元),共获利40+80=120(万元).
故选:D
2.B
【解析】由题意得图像上三点:,
对于A选项:y=0.2x,将三点代入y=0.2x,
当时,函数值与0.76相差较大;
对于B选项:,将三点代入,
当时,函数值与0.76相差仅有0.04;
对于C选项:y=x2+2x,将三点代入y=x2+2x,
当时,函数值都与实际数值相差较大;
对于D选项:,将三点代入,
当时,函数值都与0.76相差较大;
综上:沙漠增加值y(万公顷)关于年数x(年)的函数关系较为近似的是.
故选:B.
3.D
【解析】由题意,令,解得或,
不妨设,代入可得.
故选:D.
4.D
【解析】令,则方程只有一个正根,
当方程有唯一根时,则,此时根为符合题意;
当方程有一正一负根或一正根和0根时,有,则.
综上所述,或
故选:D
5.B
【解析】对于A,函数是指数函数,增长速度很快,且在时,时,代入值偏差较大,不符合要求;
对于B,函数,是对数函数,增长速度缓慢,且在时,时,基本符合要求;
对于C,函数是二次函数,且当时,时,代入值偏差较大,不符合要求;
对于D,函数,当时,不符合要求,
故选:B.
6.B
【解析】因为指数函数是几何级数增长,当x越来越大时,增长速度最快.
故选:B.
7.C
【解析】函数经过点,,∴,
∴,
令,则
所以函数的零点是0和.
故选:C.
8.C
【解析】由图知,“生活费收入指数”减去“生活价格指数”的差是逐年增大的,故①正确;
“生活费收入指数”在2014~2015年最陡;故②正确;
“生活价格指数”在2015~2016年最平缓,故③不正确;
“生活价格指数”略呈下降,而“生活费收入指数”呈上升趋势,故④正确.
故选:C.
9.BD
【解析】大包装300克8.4元,则等价为100克2.8元,小包装100克3元,则买大包装实惠,故B正确,
卖1大包的盈利8.4-0.7-1.8×3=2.3(元),卖1小包盈利3-0.5-1.8=0.7(元),则卖3小包盈利0.7×3=2.1(元),则卖1大包比卖3小包盈利多,故D正确.
故选:BD
10.ABC
【解析】因为函数恰有2个零点,
所以函数的图象与直线恰有两个交点,
画出函数的图象如图:
由图可知,或,结合选项,因此可以为-1,0,1.
故选:ABC.
11.ABCD
【解析】由题图知甲厂制版费为1千元,印刷费平均每个为0.5元,故A正确;
设甲厂的费用与证书数量满足的函数关系式为,
代入点,可得,解得,
所以甲厂的费用与证书数量满足的函数关系式为,故B正确;
当印制证书数量不超过2千个时,乙厂的印刷费平均每个为元,故C正确;
设当时,设与之间的函数关系式为
代入点,可得,解得,
所以当时,与之间的函数关系式为,故D正确.
故选:ABCD.
12.BCD
【解析】由函数解析式可得图象如下:
∴由图知:,,而当时,有,即或2,
∴,而知:,
∴,.
故选:BCD
13.
【解析】,,,
所以下一个有根区间为.
故答案为:
14.
【解析】设,则,解得:,
即的取值范围为.
故答案为:.
15.2250
【解析】设彩电的原价为a元,∴a(1+40%)·80%-a=270,∴0.12a=270,解得a=2
250.
∴每台彩电的原价为2
250元.
故答案为:2250.
16.
【解析】为开口方向向上,对称轴为的二次函数,
,即,解得:,即实数的取值范围为.
故答案为:.
17.答案见解析
【解析】作出函数的图象如图所示,
当或时,方程实数根有两个.
当时,方程实数根有三个.
当时,方程实数根有四个.
当时,方程无实数根.
18.奖励模型能完全符合公司的要求,答案见解析.
【解析】解:由题意,符合公司要求的模型需同时满足:
当x∈[10,1000]时,①函数为增函数;②函数的最大值不超过5;③y≤x·25%.
(1)对于y=0.025x,易知满足①,但当x>200时,y>5,不满足公司的要求;
(2)对于y=1.003x,易知满足①,但当x>538时,不满足公司的要求;
(3)对于,易知满足①.
当x∈[10,1000]时,y≤ln1000+1.
下面证明ln1000+1<5.
因为ln1000+1-5=ln1000-4=
(ln1000-8)=(ln1000-ln2981)<0,满足②.
再证明lnx+1≤x·25%,即2lnx+4-x≤0.
设F(x)=2lnx+4-x,则F′(x)=
-1=<0,x∈[10,1000],
所以F(x)在[10,1000]上为减函数,
F(x)max=F(10)=2ln10+4-10=2ln10-6=2(ln10-3)<0,满足③.
综上,奖励模型能完全符合公司的要求.
19.(1);(2),另一个零点为4.
【解析】(1)由题意得,所以,解得.
(2)由(1)可知,
所以方程的根,二次函数的零点是,
∴二次函数的一个零点是,
∴方程的一个根为2,
∴,解得,
∴,解得或,
所以二次函数的另一个零点为4.
20.,图见解析.
【解析】如图,过点A,D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.
因为四边形ABCD是等腰梯形,底角为45°,,所以BG=AG=DH=HC=2.
又BC=7,所以AD=GH=3.
当点F在BG上,即x∈[0,2]时,;
当点F在GH(不包括点G)上,即x∈(2,5]时,;
当点F在HC(不包括点H)上,即x∈(5,7]时,.
综上,得左边部分的面积y关于x的函数解析式为,
其大致图象如图所示.
21.(1),;(2)或.
【解析】(1)由为减函数可得,又,解得;
(2)图②中
,函数的图象如图所示.
由图象可知使有且仅有一解,则或.
22.
【解析】令,则原方程等价为有正根,又,
知此方程有两个正根,则应满足,
即,解得.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
