湖北省长阳土家族自治县第一高级中学2012届高三5月适应性考试数学(理)试题
文档属性
| 名称 | 湖北省长阳土家族自治县第一高级中学2012届高三5月适应性考试数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 343.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-22 00:00:00 | ||
图片预览



文档简介
(总分:150分;考试时间:120分钟)
一、选择题:本小题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,, 则使M∩N=N成立的的值是 ( )
A.1 B.0 C.- 1 D.1或-1
2.已知复数,则·i在复平面内对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.阅读右面的程序框图,则输出的= ( )
A.14 B.20
C.30 D.55
4. 下列命题错误的是 ( )
A.对于命题p:,使得,则为:对均有
B.命题“若"的逆否命题为“若x≠1,则"
C.“x>2"是“"的充分不必要条件
D.若是假命题,则均为假命题
5.下列函数中既是偶函数,又是区间[-1,0]上的减函数的是 ( )
A. B.
C. D.
6.已知二项式展开式中,前三项的二项式系数和是56,则展开式中的常数项为( )
A. B. C. D.
7.已知两点为坐标原点,点在第二象限,且
设等于 ( )
A. B.2 C.1 D.
8.椭圆的焦点为和,过点的直线交椭圆于两点,,,则椭圆的离心率为( )
A. B. C. D.
9.某个体企业的一个车间有8名工人,以往每人年薪为1万元,从今年起,计划每人的年薪都比上一年增加20%,另外,每年新招3名工人,每名新工人的第一年的年薪为8千元,第二年起与老工人的年薪相同.若以今年为第一年,如果将第n年企业付给工人的工资总额y(万元)表示成n的函数,则其表达式为
A.y=(3n+5)1.2n+2.4 B.y=8×1.2n+2.4n
C.y=(3n+8)1.2n+2.4 D.y=(3n+5)1.2n-1+2.4
10. 给出定义:若(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数的四个论断:
①; ②
③ ④的定义域为R,值域是[一].
则其中论断正确的序号是
A.①② B.①③ C.②④ D.③④
二、填空题:本小题共6小题,考生共需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.
(一)必考题(11—14题)
11.函数在点处的切线与函数围成的图形的面积等于 .
12. 某几何体的三视图如图所示,其正视图为矩形,
侧视图为等腰直角三角形,俯视图为直角梯形,
则这个几何体的体积为 _____
13.已知点P的坐标,
过点P的直线l与圆相交于A、B两点,则的最小值为 .
14. 甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球,先从甲罐中随机取出一球放入乙罐,分别以表示甲罐中取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以表示由乙罐中取出的球是红球的事件,则下列结论中正确的是 (只填写正确结论的编号)
①; ②; ③事件与事件相互独立; ④是两两互斥事件;
⑤的值不能确定,因为它与中究竟哪一个发生有关.
(二)选考题(请考生在第15、16两题中任选一题作答)
15.如图,A,B是圆O上的两点,且OA⊥OB,OA=2,
C为OA的中点,连接BC并延长交圆O于点D,则CD= .
(第15题图)
16.已知直线与圆相交于AB,则以AB为直径的圆的面积为 .
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤。
17. (本小题满分12分)已知向量.记
( I ) 若,求的值;
(Ⅱ) 在ABC中,角A、B、C的对边分别是a、b、c,且满足
,若,试判断ABC的形状.
18.(本小题满分12分) 已知等差数列数列的前项和为,等比数列的各项均为正数,公比是,且满足:.
(Ⅰ)求与;
(Ⅱ)设,若是单调递增数列,求的取值范围.
19.(本小题满分12分)如图,在四棱锥中,底面为菱形,
,为的中点..
(I)点在线段上,,试确定的值,使平面;
(II)在(I)的条件下,若平面平面ABCD,求二面角的大小.
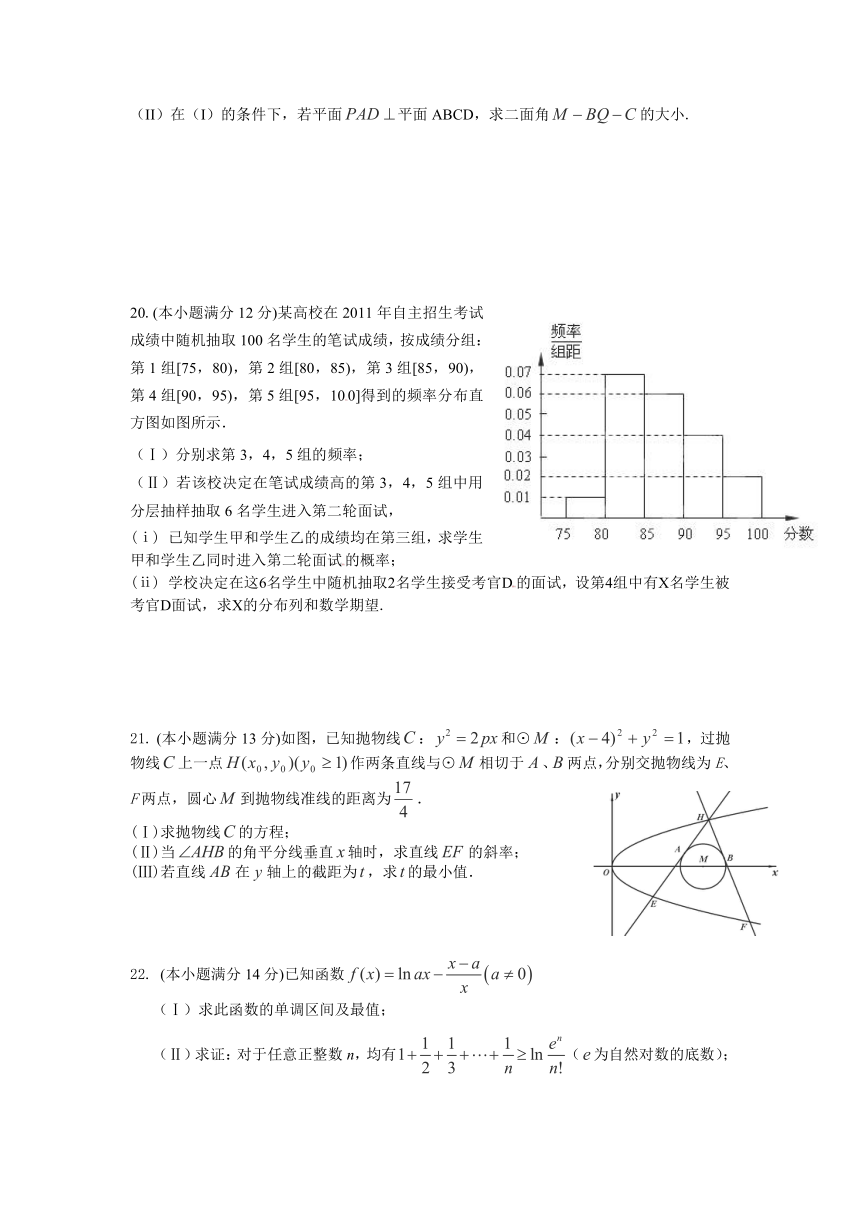
20.(本小题满分12分)某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ) 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
(ⅱ) 学校决定在这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有X名学生被考官D面试,求X的分布列和数学期望.
21. (本小题满分13分)如图,已知抛物线:和⊙:,过抛物线上一点作两条直线与⊙相切于、两点,分别交抛物线为E、F两点,圆心到抛物线准线的距离为.
(Ⅰ)求抛物线的方程;
(Ⅱ)当的角平分线垂直轴时,求直线的斜率;
(Ⅲ)若直线在轴上的截距为,求的最小值.
22. (本小题满分14分)已知函数
(Ⅰ)求此函数的单调区间及最值;
(Ⅱ)求证:对于任意正整数n,均有(为自然对数的底数);
(Ⅲ)当a=1时,是否存在过点(1,-1)的直线与函数的图象相切? 若存在,有多少条?若不存在,说明理由.
五月适应性考试答案
(Ⅱ) 根据正弦定理知:
∵ ∴ 或或
而,所以,因此ABC为等边三角形.……………12分
18.(Ⅰ)由已知可得,消去得:,解得或
(舍),从而
(Ⅱ)由(1)知:.
∵对任意的恒成立, 即:恒成立,整理得:
对任意的恒成立,即:对任意的恒成立.
∵ 在区间上单调递增,.
的取值范围为.
19.解: (1)当时,平面
下面证明:若平面,连交于
由可得,,
.........2分
平面,平面,平面平面,
........................4分
即: ......6分
(2)由PA=PD=AD=2, Q为AD的中点,则PQ⊥AD。.7分
又平面PAD⊥平面ABCD,所以PQ⊥平面ABCD,连BD,
四边形ABCD为菱形,
∵AD=AB, ∠BAD=60°△ABD为正三角形,
Q为AD中点, ∴AD⊥BQ............8分
以Q为坐标原点,分别以QA、QB、QP所在的直线为
轴,建立如图所示的坐标系,则各点坐标为
A(1,0,0),B(),Q(0,0,0),P(0,0,)
设平面MQB的法向量为,可得,
取z=1,解得 ………10分
取平面ABCD的法向量设所求二面角为,
则 故二面角的大小为60°..............12分
20.解:(1) 第三组的频率为0.065=0.3;
第四组的频率为0.045=0.2;第五组的频率为0.025=0.1.…………3分
(2) (ⅰ) 设M:学生甲和学生乙同时进入第二轮面试 ……6分
X 0 1 2
P
(ⅱ)
……12分
21.(Ⅰ)∵点到抛物线准线的距离为,∴,即抛物线的方程为.………………3分
(Ⅱ)法一:∵当的角平分线垂直轴时,点,∴,
设,,
∴,∴ ,
∴. 6分
. 8分
法二:∵当的角平分线垂直轴时,点,∴,可得,,∴直线的方程为,
联立方程组,得,
∵
∴,. 6分
同理可得,,∴. 8分
(Ⅲ)设点,,.
以为圆心,为半径的圆方程为, ①
⊙方程:. ②
①-②得:
直线的方程为. 9分
当时,直线在轴上的截距,
∵关于的函数在单调递增,
∴ 12分
22、(Ⅰ)解:由题意 . ………………1分
当时,函数的定义域为,
此时函数在上是减函数,在上是增函数,
,无最大值.………………3分
当时,函数的定义域为,
此时函数在上是减函数,在上是增函数,
,无最大值.………………5分
(Ⅱ)取,由⑴知,
故,
取,则.………………9分
(Ⅲ)假设存在这样的切线,设其中一个切点,
∴切线方程:,将点坐标代入得:
,即, ①
设,则.………………12分
,
tesoon
天·星om
权
天·星om
权
Tesoon.com
天星版权
tesoon
tesoon
tesoon
天星
一、选择题:本小题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,, 则使M∩N=N成立的的值是 ( )
A.1 B.0 C.- 1 D.1或-1
2.已知复数,则·i在复平面内对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.阅读右面的程序框图,则输出的= ( )
A.14 B.20
C.30 D.55
4. 下列命题错误的是 ( )
A.对于命题p:,使得,则为:对均有
B.命题“若"的逆否命题为“若x≠1,则"
C.“x>2"是“"的充分不必要条件
D.若是假命题,则均为假命题
5.下列函数中既是偶函数,又是区间[-1,0]上的减函数的是 ( )
A. B.
C. D.
6.已知二项式展开式中,前三项的二项式系数和是56,则展开式中的常数项为( )
A. B. C. D.
7.已知两点为坐标原点,点在第二象限,且
设等于 ( )
A. B.2 C.1 D.
8.椭圆的焦点为和,过点的直线交椭圆于两点,,,则椭圆的离心率为( )
A. B. C. D.
9.某个体企业的一个车间有8名工人,以往每人年薪为1万元,从今年起,计划每人的年薪都比上一年增加20%,另外,每年新招3名工人,每名新工人的第一年的年薪为8千元,第二年起与老工人的年薪相同.若以今年为第一年,如果将第n年企业付给工人的工资总额y(万元)表示成n的函数,则其表达式为
A.y=(3n+5)1.2n+2.4 B.y=8×1.2n+2.4n
C.y=(3n+8)1.2n+2.4 D.y=(3n+5)1.2n-1+2.4
10. 给出定义:若(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数的四个论断:
①; ②
③ ④的定义域为R,值域是[一].
则其中论断正确的序号是
A.①② B.①③ C.②④ D.③④
二、填空题:本小题共6小题,考生共需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.
(一)必考题(11—14题)
11.函数在点处的切线与函数围成的图形的面积等于 .
12. 某几何体的三视图如图所示,其正视图为矩形,
侧视图为等腰直角三角形,俯视图为直角梯形,
则这个几何体的体积为 _____
13.已知点P的坐标,
过点P的直线l与圆相交于A、B两点,则的最小值为 .
14. 甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球,先从甲罐中随机取出一球放入乙罐,分别以表示甲罐中取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以表示由乙罐中取出的球是红球的事件,则下列结论中正确的是 (只填写正确结论的编号)
①; ②; ③事件与事件相互独立; ④是两两互斥事件;
⑤的值不能确定,因为它与中究竟哪一个发生有关.
(二)选考题(请考生在第15、16两题中任选一题作答)
15.如图,A,B是圆O上的两点,且OA⊥OB,OA=2,
C为OA的中点,连接BC并延长交圆O于点D,则CD= .
(第15题图)
16.已知直线与圆相交于AB,则以AB为直径的圆的面积为 .
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤。
17. (本小题满分12分)已知向量.记
( I ) 若,求的值;
(Ⅱ) 在ABC中,角A、B、C的对边分别是a、b、c,且满足
,若,试判断ABC的形状.
18.(本小题满分12分) 已知等差数列数列的前项和为,等比数列的各项均为正数,公比是,且满足:.
(Ⅰ)求与;
(Ⅱ)设,若是单调递增数列,求的取值范围.
19.(本小题满分12分)如图,在四棱锥中,底面为菱形,
,为的中点..
(I)点在线段上,,试确定的值,使平面;
(II)在(I)的条件下,若平面平面ABCD,求二面角的大小.
20.(本小题满分12分)某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ) 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
(ⅱ) 学校决定在这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有X名学生被考官D面试,求X的分布列和数学期望.
21. (本小题满分13分)如图,已知抛物线:和⊙:,过抛物线上一点作两条直线与⊙相切于、两点,分别交抛物线为E、F两点,圆心到抛物线准线的距离为.
(Ⅰ)求抛物线的方程;
(Ⅱ)当的角平分线垂直轴时,求直线的斜率;
(Ⅲ)若直线在轴上的截距为,求的最小值.
22. (本小题满分14分)已知函数
(Ⅰ)求此函数的单调区间及最值;
(Ⅱ)求证:对于任意正整数n,均有(为自然对数的底数);
(Ⅲ)当a=1时,是否存在过点(1,-1)的直线与函数的图象相切? 若存在,有多少条?若不存在,说明理由.
五月适应性考试答案
(Ⅱ) 根据正弦定理知:
∵ ∴ 或或
而,所以,因此ABC为等边三角形.……………12分
18.(Ⅰ)由已知可得,消去得:,解得或
(舍),从而
(Ⅱ)由(1)知:.
∵对任意的恒成立, 即:恒成立,整理得:
对任意的恒成立,即:对任意的恒成立.
∵ 在区间上单调递增,.
的取值范围为.
19.解: (1)当时,平面
下面证明:若平面,连交于
由可得,,
.........2分
平面,平面,平面平面,
........................4分
即: ......6分
(2)由PA=PD=AD=2, Q为AD的中点,则PQ⊥AD。.7分
又平面PAD⊥平面ABCD,所以PQ⊥平面ABCD,连BD,
四边形ABCD为菱形,
∵AD=AB, ∠BAD=60°△ABD为正三角形,
Q为AD中点, ∴AD⊥BQ............8分
以Q为坐标原点,分别以QA、QB、QP所在的直线为
轴,建立如图所示的坐标系,则各点坐标为
A(1,0,0),B(),Q(0,0,0),P(0,0,)
设平面MQB的法向量为,可得,
取z=1,解得 ………10分
取平面ABCD的法向量设所求二面角为,
则 故二面角的大小为60°..............12分
20.解:(1) 第三组的频率为0.065=0.3;
第四组的频率为0.045=0.2;第五组的频率为0.025=0.1.…………3分
(2) (ⅰ) 设M:学生甲和学生乙同时进入第二轮面试 ……6分
X 0 1 2
P
(ⅱ)
……12分
21.(Ⅰ)∵点到抛物线准线的距离为,∴,即抛物线的方程为.………………3分
(Ⅱ)法一:∵当的角平分线垂直轴时,点,∴,
设,,
∴,∴ ,
∴. 6分
. 8分
法二:∵当的角平分线垂直轴时,点,∴,可得,,∴直线的方程为,
联立方程组,得,
∵
∴,. 6分
同理可得,,∴. 8分
(Ⅲ)设点,,.
以为圆心,为半径的圆方程为, ①
⊙方程:. ②
①-②得:
直线的方程为. 9分
当时,直线在轴上的截距,
∵关于的函数在单调递增,
∴ 12分
22、(Ⅰ)解:由题意 . ………………1分
当时,函数的定义域为,
此时函数在上是减函数,在上是增函数,
,无最大值.………………3分
当时,函数的定义域为,
此时函数在上是减函数,在上是增函数,
,无最大值.………………5分
(Ⅱ)取,由⑴知,
故,
取,则.………………9分
(Ⅲ)假设存在这样的切线,设其中一个切点,
∴切线方程:,将点坐标代入得:
,即, ①
设,则.………………12分
,
tesoon
天·星om
权
天·星om
权
Tesoon.com
天星版权
tesoon
tesoon
tesoon
天星
同课章节目录
