2020-2021学年高一数学人教A版必修4第一章1.3三角函数的诱导公式课件(共16张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修4第一章1.3三角函数的诱导公式课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 399.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 21:20:32 | ||
图片预览






文档简介
1.3三角函数的诱导公式
问题提出
1.任意角α的正弦、余弦、正切是怎样定义的?
α的终边
P(x,y)
O
x
y
2. 2kπ+α(k∈Z)与α的三角函数之间的关系是什么?
公式一:
( )
4.利用公式一,可将任意角的三角函数值,转化为00~3600范围内的三角函数值.其中锐角的三角函数可以查表计算,而对于900~3600范围内的三角函数值,如何转化为锐角的三角函数值,是我们需要研究和解决的问题.
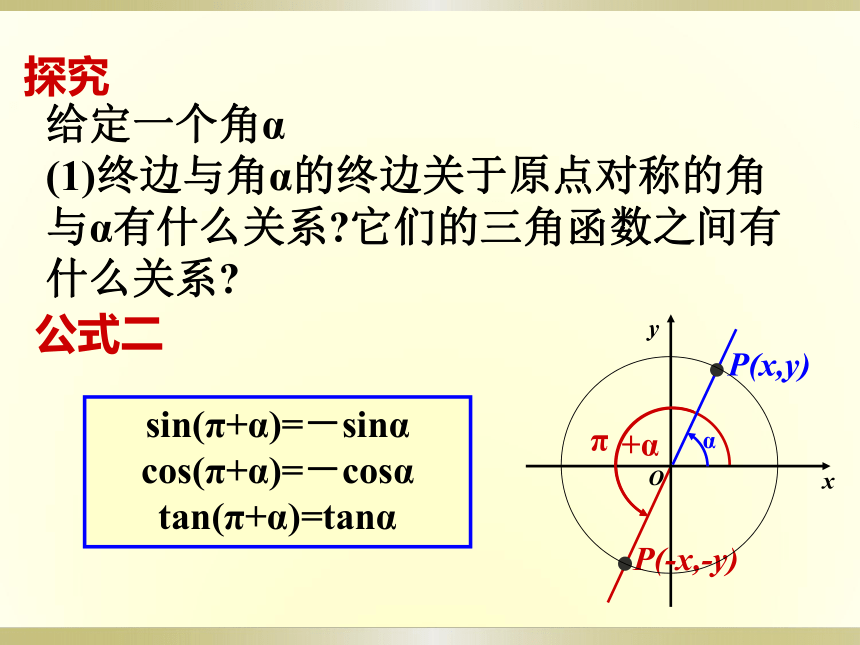
给定一个角α
(1)终边与角α的终边关于原点对称的角与α有什么关系?它们的三角函数之间有什么关系?
探究
+α
y
α
x
O
P(x,y)
π
P(-x,-y)
公式二
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
(2)终边与角α的终边关于x轴对称的角与α有什么关系?它们的三角函数之间有什么关系?
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
公式三
y
α
x
O
P(x,y)
-α
P(x,-y)
(2)终边与角α的终边关于y轴对称的角与α有什么关系?它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
P(-x,y)
α
π-α
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
公式四
公式二
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
公式三
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
公式四
α+k·2π(k∈Z),-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
例1.利用公式求下列三角函数值:
例2 化简
利用公式一~四把任意角的三角函数转化为锐角函数,一般可按下面步骤进行:
任意负角的
三角函数
任意正角的
三角函数
用公式
三或一
锐角三
角函数
用公式
二或四
0~2π的角的三角函数
用公式一
练习
将下列三角函数转化为锐角三角函数,并填在题中横线上
将下列三角函数转化为锐角三角函数,并填在题中横线上:
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
小结
三角函数的诱导公式
安全教育:
要善于网上学习,不浏览不良信息;
要诚实友好交流,不侮辱欺诈他人;
要增强自护意识,不看不健康的视频;
要维护网络安全,不破坏网络秩序;
要有益身心健康,不沉溺虚拟时空。
作业
1.课本习题1.3A组1,2
2.阅读课本,体会三角函数诱导公式推导过程中的思想方法;
问题提出
1.任意角α的正弦、余弦、正切是怎样定义的?
α的终边
P(x,y)
O
x
y
2. 2kπ+α(k∈Z)与α的三角函数之间的关系是什么?
公式一:
( )
4.利用公式一,可将任意角的三角函数值,转化为00~3600范围内的三角函数值.其中锐角的三角函数可以查表计算,而对于900~3600范围内的三角函数值,如何转化为锐角的三角函数值,是我们需要研究和解决的问题.
给定一个角α
(1)终边与角α的终边关于原点对称的角与α有什么关系?它们的三角函数之间有什么关系?
探究
+α
y
α
x
O
P(x,y)
π
P(-x,-y)
公式二
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
(2)终边与角α的终边关于x轴对称的角与α有什么关系?它们的三角函数之间有什么关系?
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
公式三
y
α
x
O
P(x,y)
-α
P(x,-y)
(2)终边与角α的终边关于y轴对称的角与α有什么关系?它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
P(-x,y)
α
π-α
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
公式四
公式二
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
公式三
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
公式四
α+k·2π(k∈Z),-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
例1.利用公式求下列三角函数值:
例2 化简
利用公式一~四把任意角的三角函数转化为锐角函数,一般可按下面步骤进行:
任意负角的
三角函数
任意正角的
三角函数
用公式
三或一
锐角三
角函数
用公式
二或四
0~2π的角的三角函数
用公式一
练习
将下列三角函数转化为锐角三角函数,并填在题中横线上
将下列三角函数转化为锐角三角函数,并填在题中横线上:
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
小结
三角函数的诱导公式
安全教育:
要善于网上学习,不浏览不良信息;
要诚实友好交流,不侮辱欺诈他人;
要增强自护意识,不看不健康的视频;
要维护网络安全,不破坏网络秩序;
要有益身心健康,不沉溺虚拟时空。
作业
1.课本习题1.3A组1,2
2.阅读课本,体会三角函数诱导公式推导过程中的思想方法;
