北师大版四年级下册教案 “数学好玩”《奥运中的数学》
文档属性
| 名称 | 北师大版四年级下册教案 “数学好玩”《奥运中的数学》 |  | |
| 格式 | doc | ||
| 文件大小 | 191.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 21:52:45 | ||
图片预览

文档简介
《奥运中的数学》教学设计
教学内容
北师大版教材四年级下册“数学好玩”《奥运中的数学》
课前思考
本节课要让学生从奥运会的情境中发现并提出问题,调动已有经验分析和解决问题,发展数学思考,提升综合实践能力。这节课既考查了小数加减的的应用,又是利用数学知识解决奥运中的数学问题。
这种综合实践课程我们老师要教给学生的到底是什么?应该是借助知识的传授同时渗透数学思想。
学习目标:
1.通过教科书提供的“奥运”信息,综合运用所学的知识和方法,解决有关的实际问题。
2.通过解决体育赛场上的有关问题,体会数学和体育之间的联系,进一步体会数学的应用价值。
教学重点:
运用知识解决奥运会比赛项目的数学问题,解决问题的能力得到提高。
教学难点:
灵活解决问题和位置的猜测。
练就学生的数学头脑和眼光,提升学生的数学素养。
教学过程
谈话引入
师:同学们,你们看过奥运会吗?那你们一定知道在近几届的奥运会中,中国在金牌榜上可是名列前茅,瞧!2004年、2008年、2012年,这些成绩是通过表格和数据统计看出来的,看来,奥运中也有数学。今天我们就一起来探究奥运中的数学。(板书:奥运中的数学)
田径比赛
了解信息
师:让我们穿越时空来到2004年的田径赛场,刘翔在男子110米栏的比赛中获得了冠军,我们可以用数学的眼光看看得分显示牌。
你能看懂了吗?110mH什么意思?12.91什么意思?
解决问题
师:当时刘翔不仅获得了冠军,还打破了奥运会的记录,想知道当时的奥运会记录是12.95,刘翔比奥运会记录少用多少秒?
生:12.95-12.91=0.04(秒)
师:你是用了小数减法的数学知识来解决问题的。
师:让我们继续用数学的眼光看前三名成绩,你知道了什么?
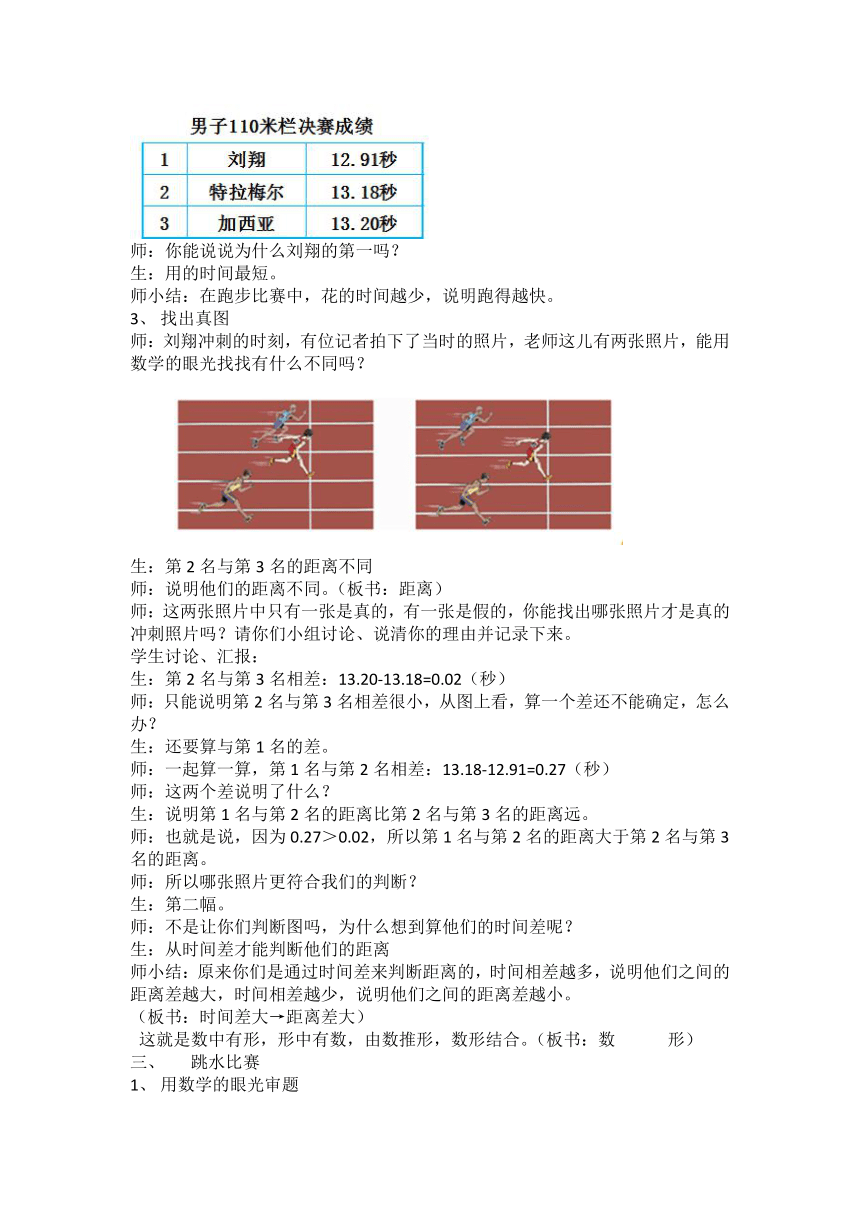
师:你能说说为什么刘翔的第一吗?
生:用的时间最短。
师小结:在跑步比赛中,花的时间越少,说明跑得越快。
找出真图
师:刘翔冲刺的时刻,有位记者拍下了当时的照片,老师这儿有两张照片,能用数学的眼光找找有什么不同吗?
生:第2名与第3名的距离不同
师:说明他们的距离不同。(板书:距离)
师:这两张照片中只有一张是真的,有一张是假的,你能找出哪张照片才是真的冲刺照片吗?请你们小组讨论、说清你的理由并记录下来。
学生讨论、汇报:
生:第2名与第3名相差:13.20-13.18=0.02(秒)
师:只能说明第2名与第3名相差很小,从图上看,算一个差还不能确定,怎么办?
生:还要算与第1名的差。
师:一起算一算,第1名与第2名相差:13.18-12.91=0.27(秒)
师:这两个差说明了什么?
生:说明第1名与第2名的距离比第2名与第3名的距离远。
师:也就是说,因为0.27>0.02,所以第1名与第2名的距离大于第2名与第3名的距离。
师:所以哪张照片更符合我们的判断?
生:第二幅。
师:不是让你们判断图吗,为什么想到算他们的时间差呢?
生:从时间差才能判断他们的距离
师小结:原来你们是通过时间差来判断距离的,时间相差越多,说明他们之间的距离差越大,时间相差越少,说明他们之间的距离差越小。
(板书:时间差大→距离差大)
这就是数中有形,形中有数,由数推形,数形结合。(板书:数 形)
跳水比赛
用数学的眼光审题
师:还想再看一个比赛吗?让我们来到2008年的跳水比赛,这是当时最后一跳前的赛况,我们可以继续用数学眼光来审题。能用数学的语言说一说何冲领先德斯帕蒂耶斯32.45分是什么意思吗?
生:何冲的分数比德斯帕蒂耶斯多32.45分。
师:为了方便,我们可以用德斯代替德斯帕蒂耶斯。
师:秦凯落后德斯帕蒂耶斯7.65分是什么意思呢?
生:秦凯比德斯少7.65分。
PPT:
2、画图分析问题
师:刚才这段话太复杂了,有没有什么更简洁、直观的方式呈现这些信息呢?
生:画图
师:画什么图?
生:线段图
师:可以用一条线段表示何冲的分数(PPT),表示德斯分数的线段比何冲的线段短一些,短多少?(32.45),能上台指一指32.45在哪里吗?
表示秦凯分数的线段比德斯短一些,短的这部分是7.65,能指一指7.65在哪吗?
师:借助图形来表示数量关系,果然更加简洁,也更直观。
3、解决问题
师:这儿有个问题:最后一跳前秦凯落后何冲多少分?
给你们1分钟快速地讨论,说清楚你的方法和理由。
小组讨论,汇报:32.45+7.65=40.1(分)
提问:为什么用加法?能从图上说说道理吗?
生:秦凯落后何冲的分数是由32.45和7.65组成,所以用加法。
师;看来图形不仅可以表示数量关系,还能找到解决问题的方法。
4、判断名次
师:你们知道吗?男子跳水决赛以6次跳水的累积总分来决定名次的,刚才只是最后一跳前的赛况,也就是前5次的情况,还有最后一跳呢,让我们看看最后一跳的成绩。
师:经过这最后一跳,最终谁得第一名?谁得第二名?谁得第三名呢?
小组讨论,说清你的理由,汇报:
师小结:何冲之前领先,最后一跳也领先,所以是第一名;最后一跳秦凯追回了98-96.9=1.1分,但是1.1<之前落后的7.65,所以秦凯还是第三名,德斯第二名。
5、画图明晰
师:这个问题仍然可以借助画图来帮助我们分析问题,在刚才最后一跳前接着往后画,德斯能不能超过何冲呢?为什么?
生:不能,因为原来就领先,最后一跳100.7>96.9,还是领先。
师:原来就领先,最后一跳又领先,说明他们的差距就更大了。
师:最终德斯比何冲落后多少分?
生:100.7+32.45—96.9=36.25(分)
师:与之前他们的分数差32.45相比,他们的分数差在增加,说明他们的差距在增大。(板书:分数差增加→差距增大)
师:秦凯能不能超过德斯?为什么?
生:不能,因为96.9+7.65>98
师:最终秦凯比德斯落后多少分?
生:96.9+7.65-98=6.55(分)
师:与之前他们的分数差7.65分相比,他们的分数差在减少,说明他们的差距在缩小。(板书:分数差减少→差距缩小)
师:从图上可以看出,最终谁得第一名?谁得第二名?谁得第三名呢?
生:何冲第一,德斯第二,秦凯第三。
师小结:我们不仅可以借助图形来研究数量之间的关系,还可以借助形来找到数据差来判断名次。这就是数中有形,形中有数,以形推数,数形结合。
课堂小结
师:这节课有什么收获?
师小结:其实,数学与我们生活是紧密相连的,生活中处处都有数学,希望同学们以后能用数学的眼光看待问题,用数学的方法分析问题,用数学的知识来解决问题。
教学内容
北师大版教材四年级下册“数学好玩”《奥运中的数学》
课前思考
本节课要让学生从奥运会的情境中发现并提出问题,调动已有经验分析和解决问题,发展数学思考,提升综合实践能力。这节课既考查了小数加减的的应用,又是利用数学知识解决奥运中的数学问题。
这种综合实践课程我们老师要教给学生的到底是什么?应该是借助知识的传授同时渗透数学思想。
学习目标:
1.通过教科书提供的“奥运”信息,综合运用所学的知识和方法,解决有关的实际问题。
2.通过解决体育赛场上的有关问题,体会数学和体育之间的联系,进一步体会数学的应用价值。
教学重点:
运用知识解决奥运会比赛项目的数学问题,解决问题的能力得到提高。
教学难点:
灵活解决问题和位置的猜测。
练就学生的数学头脑和眼光,提升学生的数学素养。
教学过程
谈话引入
师:同学们,你们看过奥运会吗?那你们一定知道在近几届的奥运会中,中国在金牌榜上可是名列前茅,瞧!2004年、2008年、2012年,这些成绩是通过表格和数据统计看出来的,看来,奥运中也有数学。今天我们就一起来探究奥运中的数学。(板书:奥运中的数学)
田径比赛
了解信息
师:让我们穿越时空来到2004年的田径赛场,刘翔在男子110米栏的比赛中获得了冠军,我们可以用数学的眼光看看得分显示牌。
你能看懂了吗?110mH什么意思?12.91什么意思?
解决问题
师:当时刘翔不仅获得了冠军,还打破了奥运会的记录,想知道当时的奥运会记录是12.95,刘翔比奥运会记录少用多少秒?
生:12.95-12.91=0.04(秒)
师:你是用了小数减法的数学知识来解决问题的。
师:让我们继续用数学的眼光看前三名成绩,你知道了什么?
师:你能说说为什么刘翔的第一吗?
生:用的时间最短。
师小结:在跑步比赛中,花的时间越少,说明跑得越快。
找出真图
师:刘翔冲刺的时刻,有位记者拍下了当时的照片,老师这儿有两张照片,能用数学的眼光找找有什么不同吗?
生:第2名与第3名的距离不同
师:说明他们的距离不同。(板书:距离)
师:这两张照片中只有一张是真的,有一张是假的,你能找出哪张照片才是真的冲刺照片吗?请你们小组讨论、说清你的理由并记录下来。
学生讨论、汇报:
生:第2名与第3名相差:13.20-13.18=0.02(秒)
师:只能说明第2名与第3名相差很小,从图上看,算一个差还不能确定,怎么办?
生:还要算与第1名的差。
师:一起算一算,第1名与第2名相差:13.18-12.91=0.27(秒)
师:这两个差说明了什么?
生:说明第1名与第2名的距离比第2名与第3名的距离远。
师:也就是说,因为0.27>0.02,所以第1名与第2名的距离大于第2名与第3名的距离。
师:所以哪张照片更符合我们的判断?
生:第二幅。
师:不是让你们判断图吗,为什么想到算他们的时间差呢?
生:从时间差才能判断他们的距离
师小结:原来你们是通过时间差来判断距离的,时间相差越多,说明他们之间的距离差越大,时间相差越少,说明他们之间的距离差越小。
(板书:时间差大→距离差大)
这就是数中有形,形中有数,由数推形,数形结合。(板书:数 形)
跳水比赛
用数学的眼光审题
师:还想再看一个比赛吗?让我们来到2008年的跳水比赛,这是当时最后一跳前的赛况,我们可以继续用数学眼光来审题。能用数学的语言说一说何冲领先德斯帕蒂耶斯32.45分是什么意思吗?
生:何冲的分数比德斯帕蒂耶斯多32.45分。
师:为了方便,我们可以用德斯代替德斯帕蒂耶斯。
师:秦凯落后德斯帕蒂耶斯7.65分是什么意思呢?
生:秦凯比德斯少7.65分。
PPT:
2、画图分析问题
师:刚才这段话太复杂了,有没有什么更简洁、直观的方式呈现这些信息呢?
生:画图
师:画什么图?
生:线段图
师:可以用一条线段表示何冲的分数(PPT),表示德斯分数的线段比何冲的线段短一些,短多少?(32.45),能上台指一指32.45在哪里吗?
表示秦凯分数的线段比德斯短一些,短的这部分是7.65,能指一指7.65在哪吗?
师:借助图形来表示数量关系,果然更加简洁,也更直观。
3、解决问题
师:这儿有个问题:最后一跳前秦凯落后何冲多少分?
给你们1分钟快速地讨论,说清楚你的方法和理由。
小组讨论,汇报:32.45+7.65=40.1(分)
提问:为什么用加法?能从图上说说道理吗?
生:秦凯落后何冲的分数是由32.45和7.65组成,所以用加法。
师;看来图形不仅可以表示数量关系,还能找到解决问题的方法。
4、判断名次
师:你们知道吗?男子跳水决赛以6次跳水的累积总分来决定名次的,刚才只是最后一跳前的赛况,也就是前5次的情况,还有最后一跳呢,让我们看看最后一跳的成绩。
师:经过这最后一跳,最终谁得第一名?谁得第二名?谁得第三名呢?
小组讨论,说清你的理由,汇报:
师小结:何冲之前领先,最后一跳也领先,所以是第一名;最后一跳秦凯追回了98-96.9=1.1分,但是1.1<之前落后的7.65,所以秦凯还是第三名,德斯第二名。
5、画图明晰
师:这个问题仍然可以借助画图来帮助我们分析问题,在刚才最后一跳前接着往后画,德斯能不能超过何冲呢?为什么?
生:不能,因为原来就领先,最后一跳100.7>96.9,还是领先。
师:原来就领先,最后一跳又领先,说明他们的差距就更大了。
师:最终德斯比何冲落后多少分?
生:100.7+32.45—96.9=36.25(分)
师:与之前他们的分数差32.45相比,他们的分数差在增加,说明他们的差距在增大。(板书:分数差增加→差距增大)
师:秦凯能不能超过德斯?为什么?
生:不能,因为96.9+7.65>98
师:最终秦凯比德斯落后多少分?
生:96.9+7.65-98=6.55(分)
师:与之前他们的分数差7.65分相比,他们的分数差在减少,说明他们的差距在缩小。(板书:分数差减少→差距缩小)
师:从图上可以看出,最终谁得第一名?谁得第二名?谁得第三名呢?
生:何冲第一,德斯第二,秦凯第三。
师小结:我们不仅可以借助图形来研究数量之间的关系,还可以借助形来找到数据差来判断名次。这就是数中有形,形中有数,以形推数,数形结合。
课堂小结
师:这节课有什么收获?
师小结:其实,数学与我们生活是紧密相连的,生活中处处都有数学,希望同学们以后能用数学的眼光看待问题,用数学的方法分析问题,用数学的知识来解决问题。
