2021-2022学年人教版九年级数学上册同步检测附答案21.2.2 公式法(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册同步检测附答案21.2.2 公式法(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 64.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 06:20:01 | ||
图片预览


文档简介
21.2.2
公式法
一、选择题(共8小题;共40分)
1.
已知关于
的一元二次方程
有两个实数根,则下列关于判别式
的判断正确的是
A.
B.
C.
D.
2.
已知关于
的一元二次方程
有两个不相等的实数根,则
的取值范围是
A.
B.
C.
D.
且
3.
关于
的方程
的根的情况描述正确的是
A.
为任何实数,方程都没有实数根
B.
为任何实数,方程都有两个不相等的实数根
C.
为任何实数,方程都有两个相等的实数根
D.
根据
的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种
4.
用公式法解一元二次方程
,正确的解应是
A.
B.
C.
D.
5.
用公式法解一元二次方程
时,计算
的结果为
A.
B.
C.
D.
6.
方程
与求根公式中相对应的
,,
的值分别是
A.
,,
B.
,,
C.
,,
D.
,,
7.
方程
的一个根是
A.
B.
C.
D.
8.
一元二次方程
的两个实数根中较大的根是
A.
B.
C.
D.
二、填空题(共4小题;共20分)
9.
若方程
有两个相等的实数根,则
?.
10.
已知关于
的一元二次方程
有两个不相等的实数根,则
的取值范围是
?.
11.
关于
的方程
有实数根,则整数
的最大值是
?.
12.
关于
的一元二次方程
的两个实数根分别为
和
,则
?;
?.
三、解答题(共7小题;共91分)
13.
用公式法解下列一元二次方程:
(1);
(2).
14.
已知关于
的一元二次方程
,
为实数.
(1)求证:方程有两个不相等的实数根;
(2)当
为何值时,方程有整数解.(直接写出三个
值,不需说明理由.)
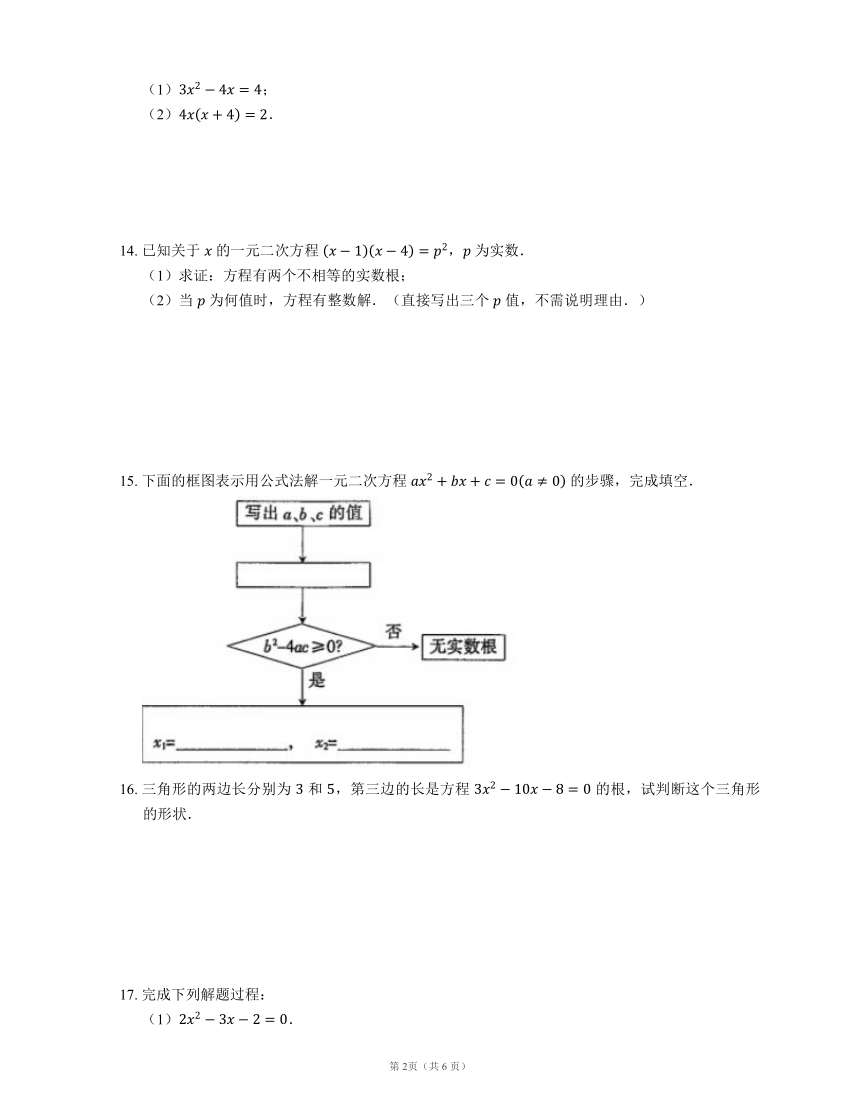
15.
下面的框图表示用公式法解一元二次方程
的步骤,完成填空.
16.
三角形的两边长分别为
和
,第三边的长是方程
的根,试判断这个三角形的形状.
17.
完成下列解题过程:
(1).
解:
?,
?,
?.
?
?
,
所以
?
?,
所以
?,
?.
(2).
解:整理,得
?.
?,
?,
?.
?
?.
所以
?
?.
(3).
解:整理,得
?.
?,
?,
?.
?
?
,
所以方程
?
实数根.
18.
关于
的一元二次方程
有实数根.
(1)求
的最大整数值.
(2)当
取最大整数值时,
求出该方程的根.
求
的值.
19.
已知等腰三角形的底边长为
,腰长是方程
的一个根,求这个三角形的面积.
答案
1.
D
2.
D
【解析】
方程有两个不相等的实数根,
,
解得
,
又
,
的取值范围为
且
.
3.
B
4.
B
5.
D
6.
C
7.
D
8.
B
9.
10.
且
11.
12.
,
13.
(1)
方程化为
.
,,.
.
方程有两个不相等的实数根.
即
??????(2)
方程化为
.
,,.
.
方程有两个不相等的实数根.
即
14.
(1)
,
整理,得
.
.
方程有两个不相等的实数根.
??????(2)
的值为
,,.
15.
求出
的值,,.
16.
解方程
得
因为
,所以这个三角形是直角三角形.
17.
(1)
;;;;;;;;.
??????(2)
;;;;;;;.
??????(3)
;;;;;;没有.
18.
(1)
根据题意,得
且
,
解得
且
.
??????(2)
①
由
可知
的最大整数值为
,
当
时,原方程为
,
,.
②
,
.
19.
用公式法解一元二次方程得
,
,,则腰长可能为
或
,当腰长为
时,该三角形三边长为
,,,不能构成三角形,舍去,
腰长只能为
,高为
,
三角形的面积是
.
第1页(共6
页)
公式法
一、选择题(共8小题;共40分)
1.
已知关于
的一元二次方程
有两个实数根,则下列关于判别式
的判断正确的是
A.
B.
C.
D.
2.
已知关于
的一元二次方程
有两个不相等的实数根,则
的取值范围是
A.
B.
C.
D.
且
3.
关于
的方程
的根的情况描述正确的是
A.
为任何实数,方程都没有实数根
B.
为任何实数,方程都有两个不相等的实数根
C.
为任何实数,方程都有两个相等的实数根
D.
根据
的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种
4.
用公式法解一元二次方程
,正确的解应是
A.
B.
C.
D.
5.
用公式法解一元二次方程
时,计算
的结果为
A.
B.
C.
D.
6.
方程
与求根公式中相对应的
,,
的值分别是
A.
,,
B.
,,
C.
,,
D.
,,
7.
方程
的一个根是
A.
B.
C.
D.
8.
一元二次方程
的两个实数根中较大的根是
A.
B.
C.
D.
二、填空题(共4小题;共20分)
9.
若方程
有两个相等的实数根,则
?.
10.
已知关于
的一元二次方程
有两个不相等的实数根,则
的取值范围是
?.
11.
关于
的方程
有实数根,则整数
的最大值是
?.
12.
关于
的一元二次方程
的两个实数根分别为
和
,则
?;
?.
三、解答题(共7小题;共91分)
13.
用公式法解下列一元二次方程:
(1);
(2).
14.
已知关于
的一元二次方程
,
为实数.
(1)求证:方程有两个不相等的实数根;
(2)当
为何值时,方程有整数解.(直接写出三个
值,不需说明理由.)
15.
下面的框图表示用公式法解一元二次方程
的步骤,完成填空.
16.
三角形的两边长分别为
和
,第三边的长是方程
的根,试判断这个三角形的形状.
17.
完成下列解题过程:
(1).
解:
?,
?,
?.
?
?
,
所以
?
?,
所以
?,
?.
(2).
解:整理,得
?.
?,
?,
?.
?
?.
所以
?
?.
(3).
解:整理,得
?.
?,
?,
?.
?
?
,
所以方程
?
实数根.
18.
关于
的一元二次方程
有实数根.
(1)求
的最大整数值.
(2)当
取最大整数值时,
求出该方程的根.
求
的值.
19.
已知等腰三角形的底边长为
,腰长是方程
的一个根,求这个三角形的面积.
答案
1.
D
2.
D
【解析】
方程有两个不相等的实数根,
,
解得
,
又
,
的取值范围为
且
.
3.
B
4.
B
5.
D
6.
C
7.
D
8.
B
9.
10.
且
11.
12.
,
13.
(1)
方程化为
.
,,.
.
方程有两个不相等的实数根.
即
??????(2)
方程化为
.
,,.
.
方程有两个不相等的实数根.
即
14.
(1)
,
整理,得
.
.
方程有两个不相等的实数根.
??????(2)
的值为
,,.
15.
求出
的值,,.
16.
解方程
得
因为
,所以这个三角形是直角三角形.
17.
(1)
;;;;;;;;.
??????(2)
;;;;;;;.
??????(3)
;;;;;;没有.
18.
(1)
根据题意,得
且
,
解得
且
.
??????(2)
①
由
可知
的最大整数值为
,
当
时,原方程为
,
,.
②
,
.
19.
用公式法解一元二次方程得
,
,,则腰长可能为
或
,当腰长为
时,该三角形三边长为
,,,不能构成三角形,舍去,
腰长只能为
,高为
,
三角形的面积是
.
第1页(共6
页)
同课章节目录
