广东省珠海市2012届高三第二次调研考试数学理(2012珠海二模)
文档属性
| 名称 | 广东省珠海市2012届高三第二次调研考试数学理(2012珠海二模) |  | |
| 格式 | zip | ||
| 文件大小 | 321.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-22 10:00:45 | ||
图片预览


文档简介
高考资源网( www.),您身边的高考专家
高考资源网( www.),您身边的高考专家
珠海市2011-2012学年度第二学期高三质量监测
理科数学
一、选择题:(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请在答题卡相应位置填涂答案)
1.已知全集,集合,则等于( C )
A., B. , C.,, D.,
2.等比数列中,,又,则公比
A. B. C.2 D.
3.在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是 ( )
A.4+8i B.8+2i C.2+4i D.4+i
4.已知a、b是实数,则“a>1,b>2”是“a+b>3且ab>2”的
A.充分而不必要条件 B.必要而不充分条件
C.充分且必要条件 D.既不充分也不必要条
5. 中,角所对的边,若,,,则
A. B. C. D.
6.已知函数满足:当x1时,=;当x<1时,=,则=
A. B. C. D.
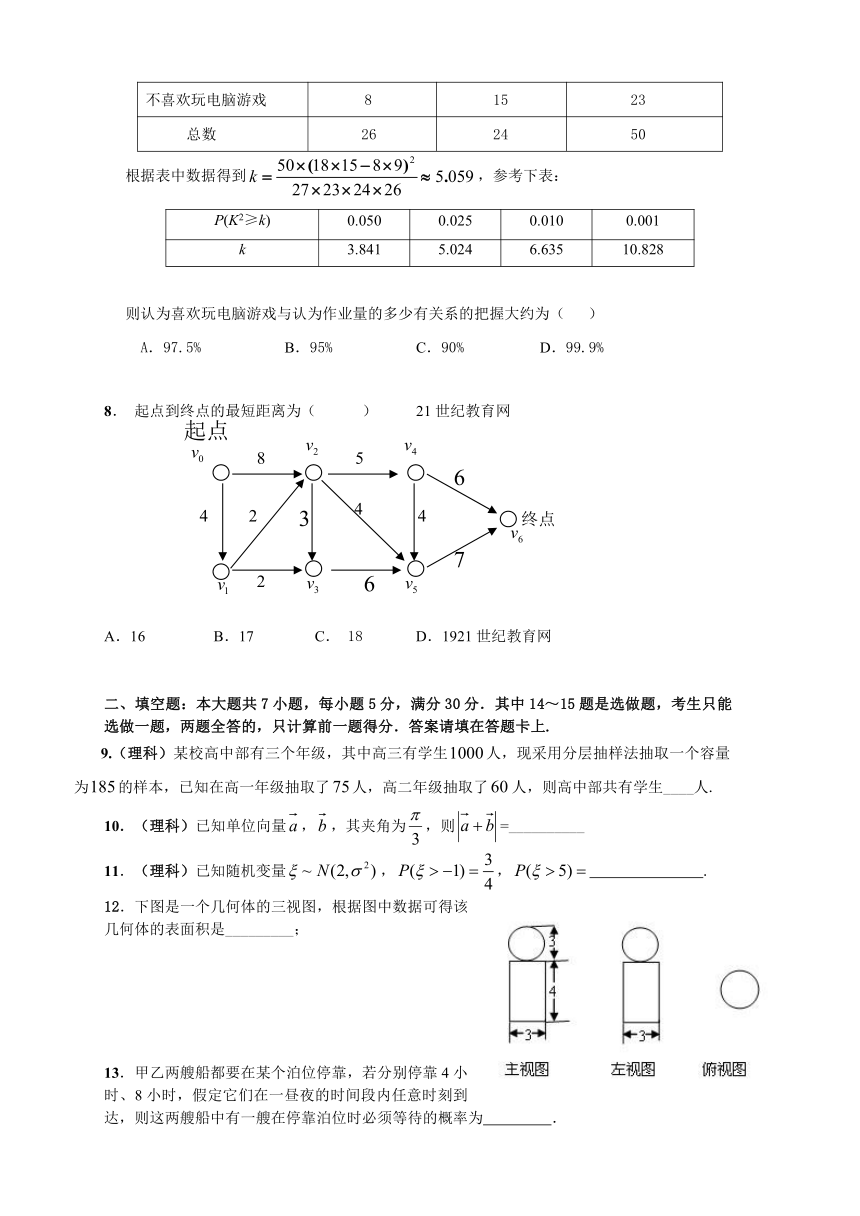
7.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
认为作业多 认为作业不多 总数
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
总数 26 24 50
根据表中数据得到,参考下表:
P(K2≥k) 0.050 0.025 0.010 0.001
k 3.841 5.024 6.635 10.828
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( )
A.97.5% B.95% C.90% D.99.9%
8. 起点到终点的最短距离为( ) 21世纪教育网
A.16 B.17 C. 18 D.1921世纪教育网
二、填空题:本大题共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.答案请填在答题卡上.
9.(理科)某校高中部有三个年级,其中高三有学生人,现采用分层抽样法抽取一个容量为的样本,已知在高一年级抽取了人,高二年级抽取了人,则高中部共有学生____人.
10.(理科)已知单位向量,,其夹角为,则=__________
11.(理科)已知随机变量,, .
12.下图是一个几何体的三视图,根据图中数据可得该几何体的表面积是_________;
13.甲乙两艘船都要在某个泊位停靠,若分别停靠4小时、8小时,假定它们在一昼夜的时间段内任意时刻到达,则这两艘船中有一艘在停靠泊位时必须等待的概率为 .
14.(坐标系与参数方程选做题).
如图,PA是圆的切线,A为切点,PBC是圆的割线,且,则 .
15.(坐标系与参数方程选做题)曲线对称的曲线的极坐标方程为 。
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)在平面直角坐标系中,以轴为始边做两个锐角,它们的终边都在第一象限内,并且分别与单位圆相交于A,B两点,已知A点的纵坐标为,B点的纵坐标为.(1)求的值;(2) 求的值.
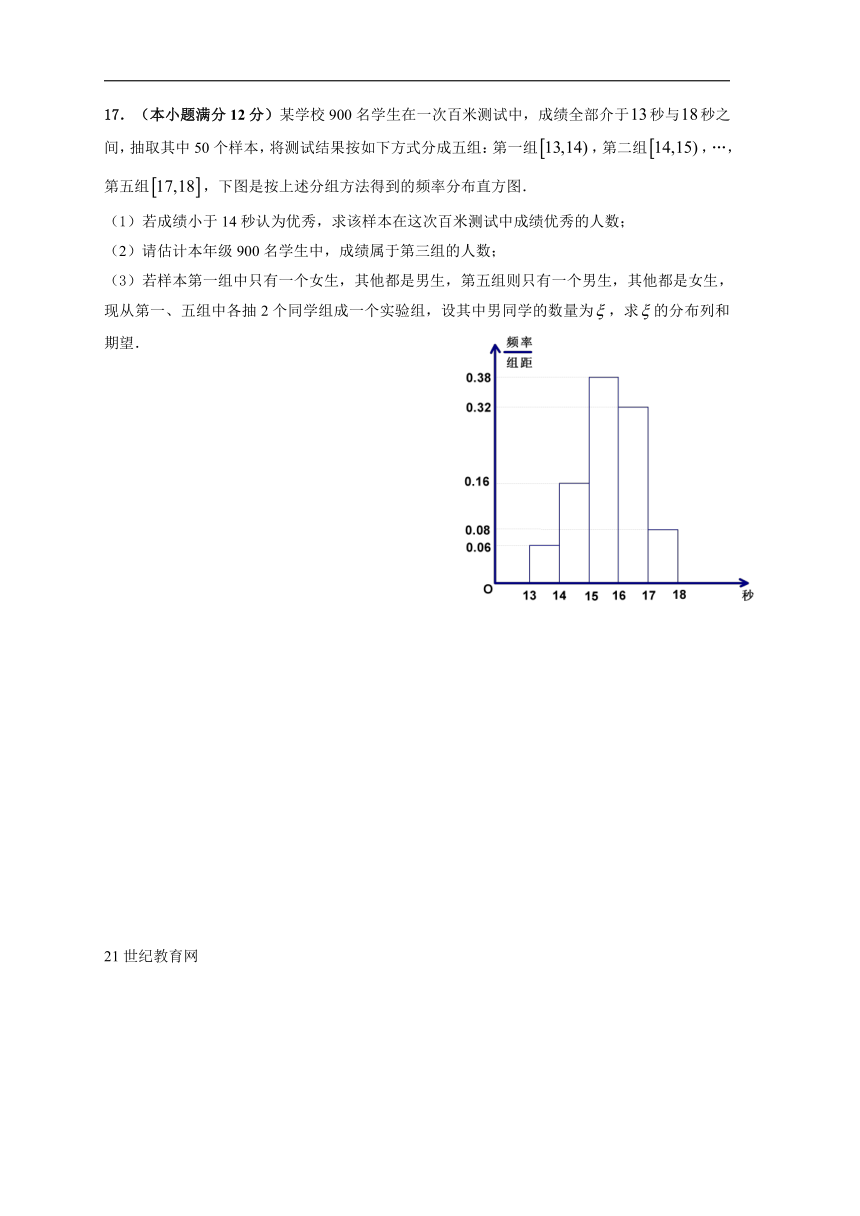
17.(本小题满分12分)某学校900名学生在一次百米测试中,成绩全部介于秒与秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组,第二组,…,第五组,下图是按上述分组方法得到的频率分布直方图.
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计本年级900名学生中,成绩属于第三组的人数;
(3)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽2个同学组成一个实验组,设其中男同学的数量为,求的分布列和期望.
21世纪教育网
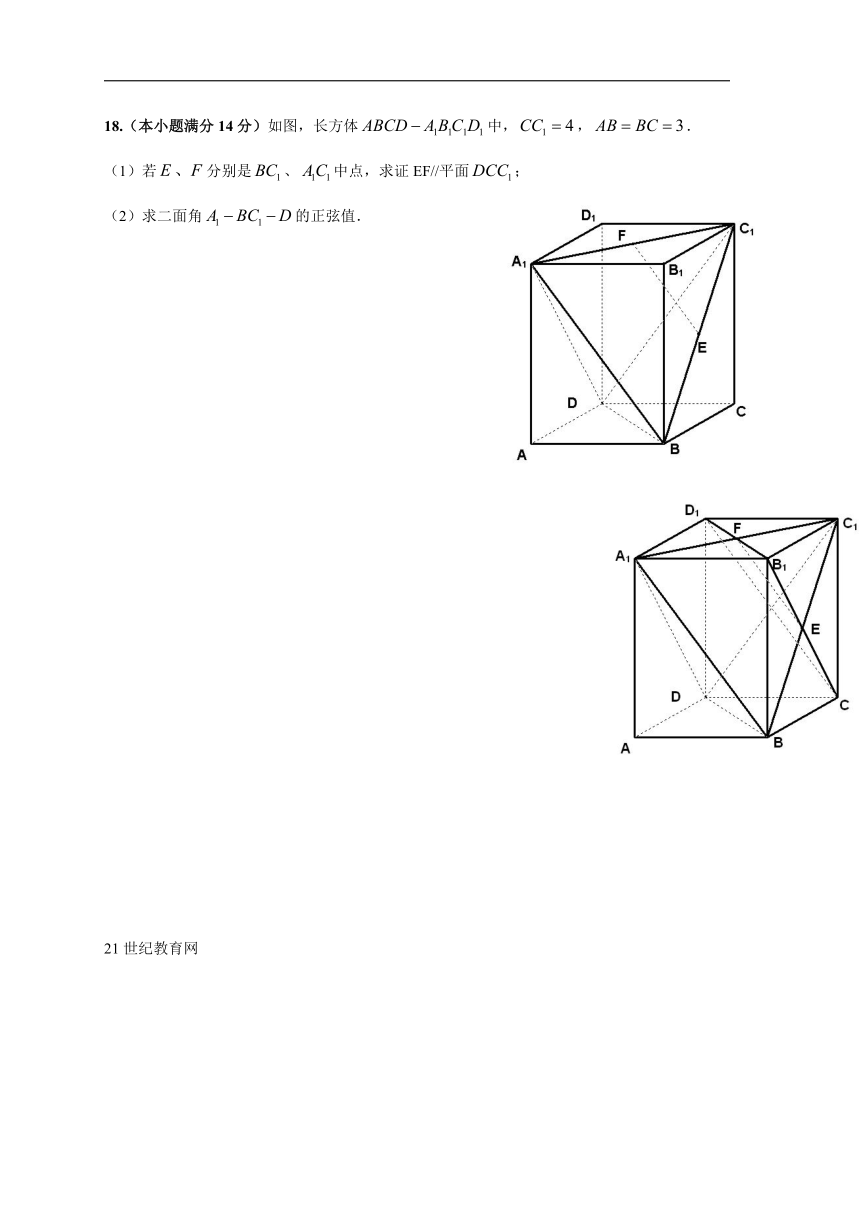
18.(本小题满分14分)如图,长方体中,,.
(1)若分别是、中点,求证EF//平面;
(2)求二面角的正弦值.
21世纪教育网
19.(本小题满分14分)已知圆C方程:(x-1)2 + y 2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且;
(1)求点P的轨迹方程;
(2)已知D为点P的轨迹曲线上第一象限弧上一点,O为原点,A、B分别为点P的轨迹曲线与轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
21世纪教育网
20.(本小题满分14分)已知函数HYPERLINK " http://www./".
(Ⅰ)若曲线经过点HYPERLINK " http://www./",曲线在点HYPERLINK " http://www./"处的切线与直线平行,求的值;
(Ⅱ)在(Ⅰ)的条件下,试求函数HYPERLINK " http://www./"(为实常数,HYPERLINK " http://www./")的极大值与极小值之差;
(Ⅲ)若在区间HYPERLINK " http://www./"内存在两个不同的极值点,求证:.
21世纪教育网
21.已知函数,,数列满足:,
,
(1) 当时,求的值并写出数列的通项公式(不要求证明);
(2) 求证:当时,;
(3) 求证:。
数学理参考答案
一、选择题:(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请在答题卡相应位置填涂答案)
1.C
2.A
3.C
4.A
5. C
6.C
7.A 21世纪教育网
8.B
二、填空题:本大题共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.答案请填在答题卡上.
9. 3700
10.
11.
12.
13.
14.
15.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.解: 本小题考查三角函数的定义、两角和的正切、二倍角的正切公式。
(1)由条件得 , …………………………………………2分
为锐角,故 且 ,同理可得 ……………4分
因此,。 …………………………………………6分
(2),
…………………………………………7分
…………8分
,在上单调递增,
且 ,∴,……………10分
同理,∴ ……………11分
从而 ………………12分
17.
解:(1)由频率分布直方图知,成绩在第一组的为优秀,频率为0.06,
人数为:50×0.06=3
所以该样本中成绩优秀的人数为3。 …………………… 3分
(2)由频率分布直方图知,成绩在第三组的频率0.38,以此估计本年级900名学生成绩属于第三组的概率为0.38,
人数为:900×0.38=342
所以估计本年级900名学生中,成绩属于第三组的人数为342。……… 7分
(3)的可能取值为1,2,3;
……… 8分
……… 9分
……… 10分
的分布列为
P 1 2 3
1/3 1/2 1/6
…… 11分
∴
…… 12分
18..
(Ⅰ)证明:连接,则长方体中,
,,
、分别是和的中点
……………………………………………………………2分
………………………………………………4分
(Ⅱ)解:(理)连接设交于,连接
正方形中,又平面
平面……………………………5分
过作于,作于,连接、
平面 ………………………………6分
平面
……………………………………8分
就是二面角…………………………10分
,
,
,……………12分
二面角的正弦值是 ……………………14分
19.
解:(1)设点坐标为,…………………………………………………………1分
则,………………………………………………………………2分
………………………………………………………………3分
因为,所以, …………………………………4分
化简得………………………………………………………………5分
所以点的轨迹方程是……………………………………………6分
(2)依题意得,点坐标为,点坐标为…………………………………7分
设点坐标为,…………………………………………8分
则四边形的面积,………………………………………9分
………………10分
……………………………………11分
又因为,所以…………………………………………………12分
所以,即
所以四边形的最大面积为,………………………………………13分
当四边形的面积取最大时,,即,
此时点坐标为………………………………………………………………14分
20. 解:(Ⅰ)HYPERLINK " http://www./",………………………1分
直线的斜率为2,曲线在点处的切线的斜率为,
……① ………………………………………2分
曲线经过点,
……② ………………………………………3分
由①②得: ……………………………………………………………………4分
(Ⅱ)由(Ⅰ)知:,,, 由,或.……………5分
当,即或时,,,变化如下表
+ 0 - 0 +
极大值 极小值
由表可知:
……………7分
当即时,,,变化如下表
- 0 + 0 -
极小值 极大值
由表可知:
………………8分
综上可知:当或时,;
当时,……………………………………9分
(Ⅲ)因为在区间内存在两个极值点 ,所以 ( http: / / www. / ),
即在 ( http: / / www. / )内有两个不等的实根.
∴ …………………………………………………………11分
由 (1)+(3)得: ( http: / / www. / ), ………………………………………………………12分
由(4)得:,由(3)得: ( http: / / www. / ),
( http: / / www. / ),∴. …………………………13分
故 …………………………………………………………………………14分
21.
(1)解:, ……………………………………2分
(2)证明:设,则,
∴在上为减函数,即,即,………………4分
设,则,
∴在上为增函数,即,即,………………5分
∴当时,。 ……………………………………6分
(3)由(1)知:当时,,
同理可证:当时,,即对,恒有:。…………7分
由得:,
∴ () ………………8分
∴,,……,,
从而, …………………………………………10分
…11分
…………………13分
∴成立。 …………………14分
.
欢迎广大教师踊跃来稿,稿酬丰厚。 www.
欢迎广大教师踊跃来稿,稿酬丰厚。 www.
高考资源网( www.),您身边的高考专家
珠海市2011-2012学年度第二学期高三质量监测
理科数学
一、选择题:(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请在答题卡相应位置填涂答案)
1.已知全集,集合,则等于( C )
A., B. , C.,, D.,
2.等比数列中,,又,则公比
A. B. C.2 D.
3.在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是 ( )
A.4+8i B.8+2i C.2+4i D.4+i
4.已知a、b是实数,则“a>1,b>2”是“a+b>3且ab>2”的
A.充分而不必要条件 B.必要而不充分条件
C.充分且必要条件 D.既不充分也不必要条
5. 中,角所对的边,若,,,则
A. B. C. D.
6.已知函数满足:当x1时,=;当x<1时,=,则=
A. B. C. D.
7.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
认为作业多 认为作业不多 总数
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
总数 26 24 50
根据表中数据得到,参考下表:
P(K2≥k) 0.050 0.025 0.010 0.001
k 3.841 5.024 6.635 10.828
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( )
A.97.5% B.95% C.90% D.99.9%
8. 起点到终点的最短距离为( ) 21世纪教育网
A.16 B.17 C. 18 D.1921世纪教育网
二、填空题:本大题共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.答案请填在答题卡上.
9.(理科)某校高中部有三个年级,其中高三有学生人,现采用分层抽样法抽取一个容量为的样本,已知在高一年级抽取了人,高二年级抽取了人,则高中部共有学生____人.
10.(理科)已知单位向量,,其夹角为,则=__________
11.(理科)已知随机变量,, .
12.下图是一个几何体的三视图,根据图中数据可得该几何体的表面积是_________;
13.甲乙两艘船都要在某个泊位停靠,若分别停靠4小时、8小时,假定它们在一昼夜的时间段内任意时刻到达,则这两艘船中有一艘在停靠泊位时必须等待的概率为 .
14.(坐标系与参数方程选做题).
如图,PA是圆的切线,A为切点,PBC是圆的割线,且,则 .
15.(坐标系与参数方程选做题)曲线对称的曲线的极坐标方程为 。
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)在平面直角坐标系中,以轴为始边做两个锐角,它们的终边都在第一象限内,并且分别与单位圆相交于A,B两点,已知A点的纵坐标为,B点的纵坐标为.(1)求的值;(2) 求的值.
17.(本小题满分12分)某学校900名学生在一次百米测试中,成绩全部介于秒与秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组,第二组,…,第五组,下图是按上述分组方法得到的频率分布直方图.
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计本年级900名学生中,成绩属于第三组的人数;
(3)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽2个同学组成一个实验组,设其中男同学的数量为,求的分布列和期望.
21世纪教育网
18.(本小题满分14分)如图,长方体中,,.
(1)若分别是、中点,求证EF//平面;
(2)求二面角的正弦值.
21世纪教育网
19.(本小题满分14分)已知圆C方程:(x-1)2 + y 2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且;
(1)求点P的轨迹方程;
(2)已知D为点P的轨迹曲线上第一象限弧上一点,O为原点,A、B分别为点P的轨迹曲线与轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
21世纪教育网
20.(本小题满分14分)已知函数HYPERLINK " http://www./".
(Ⅰ)若曲线经过点HYPERLINK " http://www./",曲线在点HYPERLINK " http://www./"处的切线与直线平行,求的值;
(Ⅱ)在(Ⅰ)的条件下,试求函数HYPERLINK " http://www./"(为实常数,HYPERLINK " http://www./")的极大值与极小值之差;
(Ⅲ)若在区间HYPERLINK " http://www./"内存在两个不同的极值点,求证:.
21世纪教育网
21.已知函数,,数列满足:,
,
(1) 当时,求的值并写出数列的通项公式(不要求证明);
(2) 求证:当时,;
(3) 求证:。
数学理参考答案
一、选择题:(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请在答题卡相应位置填涂答案)
1.C
2.A
3.C
4.A
5. C
6.C
7.A 21世纪教育网
8.B
二、填空题:本大题共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.答案请填在答题卡上.
9. 3700
10.
11.
12.
13.
14.
15.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.解: 本小题考查三角函数的定义、两角和的正切、二倍角的正切公式。
(1)由条件得 , …………………………………………2分
为锐角,故 且 ,同理可得 ……………4分
因此,。 …………………………………………6分
(2),
…………………………………………7分
…………8分
,在上单调递增,
且 ,∴,……………10分
同理,∴ ……………11分
从而 ………………12分
17.
解:(1)由频率分布直方图知,成绩在第一组的为优秀,频率为0.06,
人数为:50×0.06=3
所以该样本中成绩优秀的人数为3。 …………………… 3分
(2)由频率分布直方图知,成绩在第三组的频率0.38,以此估计本年级900名学生成绩属于第三组的概率为0.38,
人数为:900×0.38=342
所以估计本年级900名学生中,成绩属于第三组的人数为342。……… 7分
(3)的可能取值为1,2,3;
……… 8分
……… 9分
……… 10分
的分布列为
P 1 2 3
1/3 1/2 1/6
…… 11分
∴
…… 12分
18..
(Ⅰ)证明:连接,则长方体中,
,,
、分别是和的中点
……………………………………………………………2分
………………………………………………4分
(Ⅱ)解:(理)连接设交于,连接
正方形中,又平面
平面……………………………5分
过作于,作于,连接、
平面 ………………………………6分
平面
……………………………………8分
就是二面角…………………………10分
,
,
,……………12分
二面角的正弦值是 ……………………14分
19.
解:(1)设点坐标为,…………………………………………………………1分
则,………………………………………………………………2分
………………………………………………………………3分
因为,所以, …………………………………4分
化简得………………………………………………………………5分
所以点的轨迹方程是……………………………………………6分
(2)依题意得,点坐标为,点坐标为…………………………………7分
设点坐标为,…………………………………………8分
则四边形的面积,………………………………………9分
………………10分
……………………………………11分
又因为,所以…………………………………………………12分
所以,即
所以四边形的最大面积为,………………………………………13分
当四边形的面积取最大时,,即,
此时点坐标为………………………………………………………………14分
20. 解:(Ⅰ)HYPERLINK " http://www./",………………………1分
直线的斜率为2,曲线在点处的切线的斜率为,
……① ………………………………………2分
曲线经过点,
……② ………………………………………3分
由①②得: ……………………………………………………………………4分
(Ⅱ)由(Ⅰ)知:,,, 由,或.……………5分
当,即或时,,,变化如下表
+ 0 - 0 +
极大值 极小值
由表可知:
……………7分
当即时,,,变化如下表
- 0 + 0 -
极小值 极大值
由表可知:
………………8分
综上可知:当或时,;
当时,……………………………………9分
(Ⅲ)因为在区间内存在两个极值点 ,所以 ( http: / / www. / ),
即在 ( http: / / www. / )内有两个不等的实根.
∴ …………………………………………………………11分
由 (1)+(3)得: ( http: / / www. / ), ………………………………………………………12分
由(4)得:,由(3)得: ( http: / / www. / ),
( http: / / www. / ),∴. …………………………13分
故 …………………………………………………………………………14分
21.
(1)解:, ……………………………………2分
(2)证明:设,则,
∴在上为减函数,即,即,………………4分
设,则,
∴在上为增函数,即,即,………………5分
∴当时,。 ……………………………………6分
(3)由(1)知:当时,,
同理可证:当时,,即对,恒有:。…………7分
由得:,
∴ () ………………8分
∴,,……,,
从而, …………………………………………10分
…11分
…………………13分
∴成立。 …………………14分
.
欢迎广大教师踊跃来稿,稿酬丰厚。 www.
欢迎广大教师踊跃来稿,稿酬丰厚。 www.
同课章节目录
