2021-2022学年北师大新版七年级上册数学《第4章 基本平面图形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大新版七年级上册数学《第4章 基本平面图形》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 385.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大新版七年级上册数学《第4章
基本平面图形》单元测试卷
一.选择题
1.已知,则代数式的值为( )
A.
B.
C.
D.
2.已知=,则的值为( )
A.
B.
C.
D.
3.下列各组线段中,不成比例的是( )
A.4cm、6cm、8cm、10cm
B.4cm、6cm,8cm、12cm
C.11cm、22cm、33cm、66cm
D.2cm、4cm、4cm、8cm
4.下列说法中正确的是( )
A.两个平行四边形一定相似
B.两个菱形一定相似
C.两个矩形一定相似
D.两个等腰直角三角形一定相似
5.下列图形中不一定是相似图形的是( )
A.两个等边三角形
B.两个等腰直角三角形
C.两个长方形
D.两个正方形
6.如图的两个四边形相似,则∠α的度数是( )
A.87°
B.60°
C.75°
D.120°
7.已知=,则=( )
A.
B.
C.
D.
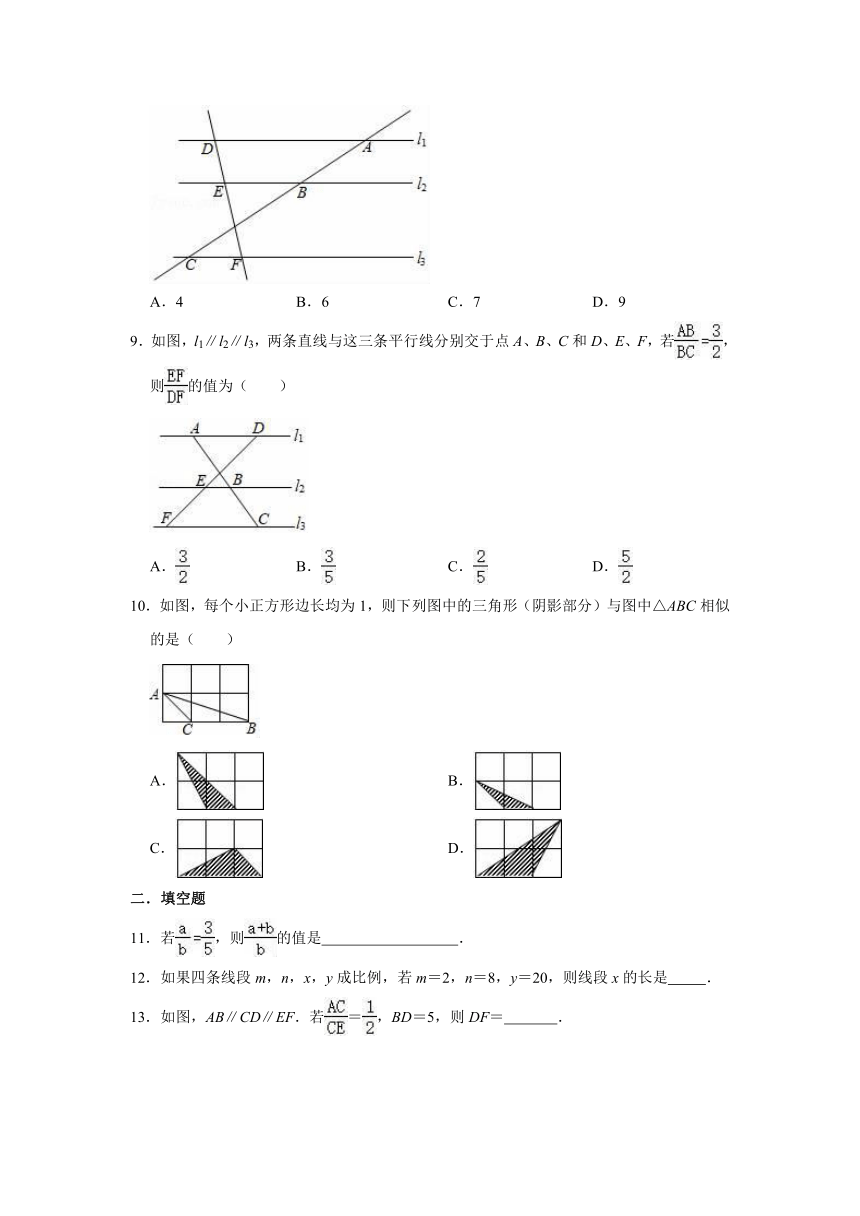
8.如图,直线l1∥l2∥l3,若AB=6,BC=9,EF=6,则DE=( )
A.4
B.6
C.7
D.9
9.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若,则的值为( )
A.
B.
C.
D.
10.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( )
A.
B.
C.
D.
二.填空题
11.若,则的值是
.
12.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长是
.
13.如图,AB∥CD∥EF.若=,BD=5,则DF=
.
14.若,则=
.
15.已知=,则的值是
.
16.某课外活动小组的同学在研究某种植物标本(如图所示)时,测得叶片①最大宽度是8cm,最大长度是16cm;叶片②最大宽度是7cm,最大长度是14cm;叶片③最大宽度约为6.5cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为
cm.
17.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似.则矩形DMNC与矩形ABCD的长与宽之比是
.
18.如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足
条件时,有△ABC∽△AED.
19.如图,AD是△ABC的中线,E是AD上一点,BE的延长线交AC于F,△ABE的面积与△DBE的面积之比是1:3,且AF=2,则FC=
.
20.(经典题)挂在墙上的中国地图与课本上的中国地图
相似的图形.
三.解答题
21.在△ABC中,点D、E分别在边AB、AC上,且AD:DB=3:2,AE:EC=1:2,直线ED和CB的延长线交于点F,求:FB:FC.
22.已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
23.已知线段a、b、c满足,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x.
24.如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为α°,β°,将菱形的“接近度”定义为|α﹣β|,于是|α﹣β|越小,菱形越接近正方形.
①若菱形的一个内角为80°,则该菱形的“接近度”为
;
②当菱形的“接近度”等于
时,菱形是正方形;
(2)设矩形的长和宽分别为m,n(m≤n),试写出矩形的“接近度”的合理定义.
25.已知==2,求和的值.
26.已知,求下列算式的值.
(1);
(2).
27.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.
(1)如果AB=6,BC=8,DF=21,求DE的长;
(2)如果DE:DF=2:5,AD=9,CF=14,求BE的长.
参考答案与试题解析
一.选择题
1.解:∵=,
∴a=b,
∴==.
故选:B.
2.解:设=k,则a=2k,b=5k.
则原式==.
故选:A.
3.解:A、4×10≠6×8,故选项错误;
B、4×2=6×8,故选项正确;
C、11×66=22×33,故选项正确;
D、2×8=4×4,故选项正确;
弧选A.
4.解:A、两个平行四边形一定相似,说法错误;
B、两个菱形一定相似,说法错误;
C、两个矩形一定相似,说法错误;
D、两个等腰直角三角形一定相似,说法正确;
故选:D.
5.解:A、两个等边三角形对应边成比例,对应角相等,一定相似,故本选项错误;
B、两个等腰直角三角形,顶角都是直角相等,夹边成比例,一定相似,故本选项错误;
C、两个长方形,四个角都是直角相等,但对应边不一定成比例,不一定相似,故本选项正确;
D、两个正方形对应边成比例,对应角相等,一定相似,故本选项错误.
故选:C.
6.解:∵两个四边形相似,
∴∠1=138°,
∵四边形的内角和等于360°,
∴∠α=360°﹣60°﹣75°﹣138°=87°,
故选:A.
7.解:∵=,
∴==,
故选:B.
8.解:∵直线l1∥l2∥l3,
∴=,即=,
∴DE=4.
故选:A.
9.解:∵l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,
∴=,
又∵,
∴==,
故选:C.
10.解:由勾股定理得:AB==,BC=2,AC==,
∴AC:BC:AB=1::,
A、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
B、三边之比:1::,图中的三角形(阴影部分)与△ABC相似;
C、三边之比为::3,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:B.
二.填空题
11.解:∵=,
∴a=b,
∴==.
故答案为:.
12.解:∵m:n=2:8=1:4,
∴x:y=1:4,
∵y=20,
∴x=5.
13.解:∵AB∥CD∥EF,
∴==,
∴DF=2BD=2×5=10.
故答案为10.
14.解:∵,
∴==,
∴=.
故答案是:.
15.解:由分比性质,得==,
故答案为:.
16.解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度:最大长度=1:2.由此可得出完整的叶片③的最大长度应是6.5×2=13cm.
故答案为:13.
17.解:设矩形ABCD的长AD=x,宽AB=y,则DM=AD=x.
∵矩形DMNC与矩形ABCD相似.
∴=,即=
即y2=x2.
∴x:y=:1.
故答案为::1.
18.解:∵DE与BC不平行,
∴∠D≠∠B,
而∠DAE=∠CAB,
∴当∠ADE=∠C或∠AED=∠B时,△ABC∽△AED.
当=时,△ABC∽△AED.
故答案为:∠ADE=∠C或∠AED=∠B或=.
19.解:作DH∥BF交AC于H,
∵AD是△ABC的中线,
∴BD=DC,
∵DH∥BF,
∴FH=HC,
∵△ABE的面积与△DBE的面积之比是1:3,
∴=,
∵DH∥BF,
∴==,
∴=,
∴FC=6AF=6×2=12;
故答案为:12.
20.解:根据相似图形的定义知,挂在墙上的中国地图与课本上的中国地图形状相同,只是大小不一定相同,
∴它们是相似图形.
三.解答题
21.解:过B作BG∥AC交EF于G,
∴△DBG∽△ADE,
∴==,
∵AE:EC=1:2,
∴BG:CE=,
∵BG∥AC,
∴△BFG∽△CFE,
∴=.
22.解:设a=2k,b=3k,c=4k,
又∵2a+3b﹣2c=10,
∴4k+9k﹣8k=10,
5k=10,
解得k=2.
∴a=4,b=6,c=8.
23.解:(1)设===k,
则a=3k,b=2k,c=6k,
所以,3k+2×2k+6k=26,
解得k=2,
所以,a=3×2=6,
b=2×2=4,
c=6×2=12;
(2)∵线段x是线段a、b的比例中项,
∴x2=ab=6×4=24,
∴线段x=2.
24.解:(1)①∵内角为80°,
∴与它相邻内角的度数为100°.
∴菱形的“接近度”=|m﹣n|=|100﹣80|=20.
②当菱形的“接近度”等于0时,菱形是正方形.
故答案为:20;0;
(2)设矩形的长和宽分别为m,n(m≤n),如矩形的“接近度”的定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当=1时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
25.解:因为==2,
可得:a=2b,c=2d,
所以=,=.
26.解:(1)∵,
∴=;
(2)∵,
∴设a=3k,则b=2k,
∴===.
27.解:(1)∵AD∥BE∥CF,
∴,
∵AB=6,BC=8,DF=21,
∴,
∴DE=9.
(2)过点D作DG∥AC,交BE于点H,交CF于点G,
则CG=BH=AD=9,
∴GF=14﹣9=5,
∵HE∥GF,
∴,
∵DE:DF=2:5,GF=5,
∴,
∴HE=2,
∴BE=9+2=11.
基本平面图形》单元测试卷
一.选择题
1.已知,则代数式的值为( )
A.
B.
C.
D.
2.已知=,则的值为( )
A.
B.
C.
D.
3.下列各组线段中,不成比例的是( )
A.4cm、6cm、8cm、10cm
B.4cm、6cm,8cm、12cm
C.11cm、22cm、33cm、66cm
D.2cm、4cm、4cm、8cm
4.下列说法中正确的是( )
A.两个平行四边形一定相似
B.两个菱形一定相似
C.两个矩形一定相似
D.两个等腰直角三角形一定相似
5.下列图形中不一定是相似图形的是( )
A.两个等边三角形
B.两个等腰直角三角形
C.两个长方形
D.两个正方形
6.如图的两个四边形相似,则∠α的度数是( )
A.87°
B.60°
C.75°
D.120°
7.已知=,则=( )
A.
B.
C.
D.
8.如图,直线l1∥l2∥l3,若AB=6,BC=9,EF=6,则DE=( )
A.4
B.6
C.7
D.9
9.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若,则的值为( )
A.
B.
C.
D.
10.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( )
A.
B.
C.
D.
二.填空题
11.若,则的值是
.
12.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长是
.
13.如图,AB∥CD∥EF.若=,BD=5,则DF=
.
14.若,则=
.
15.已知=,则的值是
.
16.某课外活动小组的同学在研究某种植物标本(如图所示)时,测得叶片①最大宽度是8cm,最大长度是16cm;叶片②最大宽度是7cm,最大长度是14cm;叶片③最大宽度约为6.5cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为
cm.
17.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似.则矩形DMNC与矩形ABCD的长与宽之比是
.
18.如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足
条件时,有△ABC∽△AED.
19.如图,AD是△ABC的中线,E是AD上一点,BE的延长线交AC于F,△ABE的面积与△DBE的面积之比是1:3,且AF=2,则FC=
.
20.(经典题)挂在墙上的中国地图与课本上的中国地图
相似的图形.
三.解答题
21.在△ABC中,点D、E分别在边AB、AC上,且AD:DB=3:2,AE:EC=1:2,直线ED和CB的延长线交于点F,求:FB:FC.
22.已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
23.已知线段a、b、c满足,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x.
24.如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为α°,β°,将菱形的“接近度”定义为|α﹣β|,于是|α﹣β|越小,菱形越接近正方形.
①若菱形的一个内角为80°,则该菱形的“接近度”为
;
②当菱形的“接近度”等于
时,菱形是正方形;
(2)设矩形的长和宽分别为m,n(m≤n),试写出矩形的“接近度”的合理定义.
25.已知==2,求和的值.
26.已知,求下列算式的值.
(1);
(2).
27.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.
(1)如果AB=6,BC=8,DF=21,求DE的长;
(2)如果DE:DF=2:5,AD=9,CF=14,求BE的长.
参考答案与试题解析
一.选择题
1.解:∵=,
∴a=b,
∴==.
故选:B.
2.解:设=k,则a=2k,b=5k.
则原式==.
故选:A.
3.解:A、4×10≠6×8,故选项错误;
B、4×2=6×8,故选项正确;
C、11×66=22×33,故选项正确;
D、2×8=4×4,故选项正确;
弧选A.
4.解:A、两个平行四边形一定相似,说法错误;
B、两个菱形一定相似,说法错误;
C、两个矩形一定相似,说法错误;
D、两个等腰直角三角形一定相似,说法正确;
故选:D.
5.解:A、两个等边三角形对应边成比例,对应角相等,一定相似,故本选项错误;
B、两个等腰直角三角形,顶角都是直角相等,夹边成比例,一定相似,故本选项错误;
C、两个长方形,四个角都是直角相等,但对应边不一定成比例,不一定相似,故本选项正确;
D、两个正方形对应边成比例,对应角相等,一定相似,故本选项错误.
故选:C.
6.解:∵两个四边形相似,
∴∠1=138°,
∵四边形的内角和等于360°,
∴∠α=360°﹣60°﹣75°﹣138°=87°,
故选:A.
7.解:∵=,
∴==,
故选:B.
8.解:∵直线l1∥l2∥l3,
∴=,即=,
∴DE=4.
故选:A.
9.解:∵l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,
∴=,
又∵,
∴==,
故选:C.
10.解:由勾股定理得:AB==,BC=2,AC==,
∴AC:BC:AB=1::,
A、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
B、三边之比:1::,图中的三角形(阴影部分)与△ABC相似;
C、三边之比为::3,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:B.
二.填空题
11.解:∵=,
∴a=b,
∴==.
故答案为:.
12.解:∵m:n=2:8=1:4,
∴x:y=1:4,
∵y=20,
∴x=5.
13.解:∵AB∥CD∥EF,
∴==,
∴DF=2BD=2×5=10.
故答案为10.
14.解:∵,
∴==,
∴=.
故答案是:.
15.解:由分比性质,得==,
故答案为:.
16.解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度:最大长度=1:2.由此可得出完整的叶片③的最大长度应是6.5×2=13cm.
故答案为:13.
17.解:设矩形ABCD的长AD=x,宽AB=y,则DM=AD=x.
∵矩形DMNC与矩形ABCD相似.
∴=,即=
即y2=x2.
∴x:y=:1.
故答案为::1.
18.解:∵DE与BC不平行,
∴∠D≠∠B,
而∠DAE=∠CAB,
∴当∠ADE=∠C或∠AED=∠B时,△ABC∽△AED.
当=时,△ABC∽△AED.
故答案为:∠ADE=∠C或∠AED=∠B或=.
19.解:作DH∥BF交AC于H,
∵AD是△ABC的中线,
∴BD=DC,
∵DH∥BF,
∴FH=HC,
∵△ABE的面积与△DBE的面积之比是1:3,
∴=,
∵DH∥BF,
∴==,
∴=,
∴FC=6AF=6×2=12;
故答案为:12.
20.解:根据相似图形的定义知,挂在墙上的中国地图与课本上的中国地图形状相同,只是大小不一定相同,
∴它们是相似图形.
三.解答题
21.解:过B作BG∥AC交EF于G,
∴△DBG∽△ADE,
∴==,
∵AE:EC=1:2,
∴BG:CE=,
∵BG∥AC,
∴△BFG∽△CFE,
∴=.
22.解:设a=2k,b=3k,c=4k,
又∵2a+3b﹣2c=10,
∴4k+9k﹣8k=10,
5k=10,
解得k=2.
∴a=4,b=6,c=8.
23.解:(1)设===k,
则a=3k,b=2k,c=6k,
所以,3k+2×2k+6k=26,
解得k=2,
所以,a=3×2=6,
b=2×2=4,
c=6×2=12;
(2)∵线段x是线段a、b的比例中项,
∴x2=ab=6×4=24,
∴线段x=2.
24.解:(1)①∵内角为80°,
∴与它相邻内角的度数为100°.
∴菱形的“接近度”=|m﹣n|=|100﹣80|=20.
②当菱形的“接近度”等于0时,菱形是正方形.
故答案为:20;0;
(2)设矩形的长和宽分别为m,n(m≤n),如矩形的“接近度”的定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当=1时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
25.解:因为==2,
可得:a=2b,c=2d,
所以=,=.
26.解:(1)∵,
∴=;
(2)∵,
∴设a=3k,则b=2k,
∴===.
27.解:(1)∵AD∥BE∥CF,
∴,
∵AB=6,BC=8,DF=21,
∴,
∴DE=9.
(2)过点D作DG∥AC,交BE于点H,交CF于点G,
则CG=BH=AD=9,
∴GF=14﹣9=5,
∵HE∥GF,
∴,
∵DE:DF=2:5,GF=5,
∴,
∴HE=2,
∴BE=9+2=11.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
