人教版数学八年级上册12.3 角的平分线的性质同步练习(word版含解析)
文档属性
| 名称 | 人教版数学八年级上册12.3 角的平分线的性质同步练习(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 662.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 06:34:43 | ||
图片预览


文档简介
12.3
角的平分线的性质
一、单选题
1.在△ABC中,∠C=90°,角平分线AD交BC于点D,BC=32,BD:CD=9:7,则D点到AB边的距离为( )
A.18
B.16
C.14
D.12
2.如图,,的平分线与的平分线相交于点,作于,若,则两平行线与间的距离为(
)
A.
B.
C.
D.
3.如图,在中,,以顶点B为圆心,适当长度为半径画弧,分别交,BC于点M,N,再分别以点M,N为圆心,以大于的长为半径作弧,两弧相交于点P;作射线BP交AC于点D,若CD=4,则点D到的距离为( )
A.4
B.3
C.
D.1
4.如图,在△ABC中,AD平分∠BAC,过B点作BE⊥AD于E,过E作EFAC交AB于F,则(
)
A.不确定
B.AF=BF
C.AFBF
D.AFBF
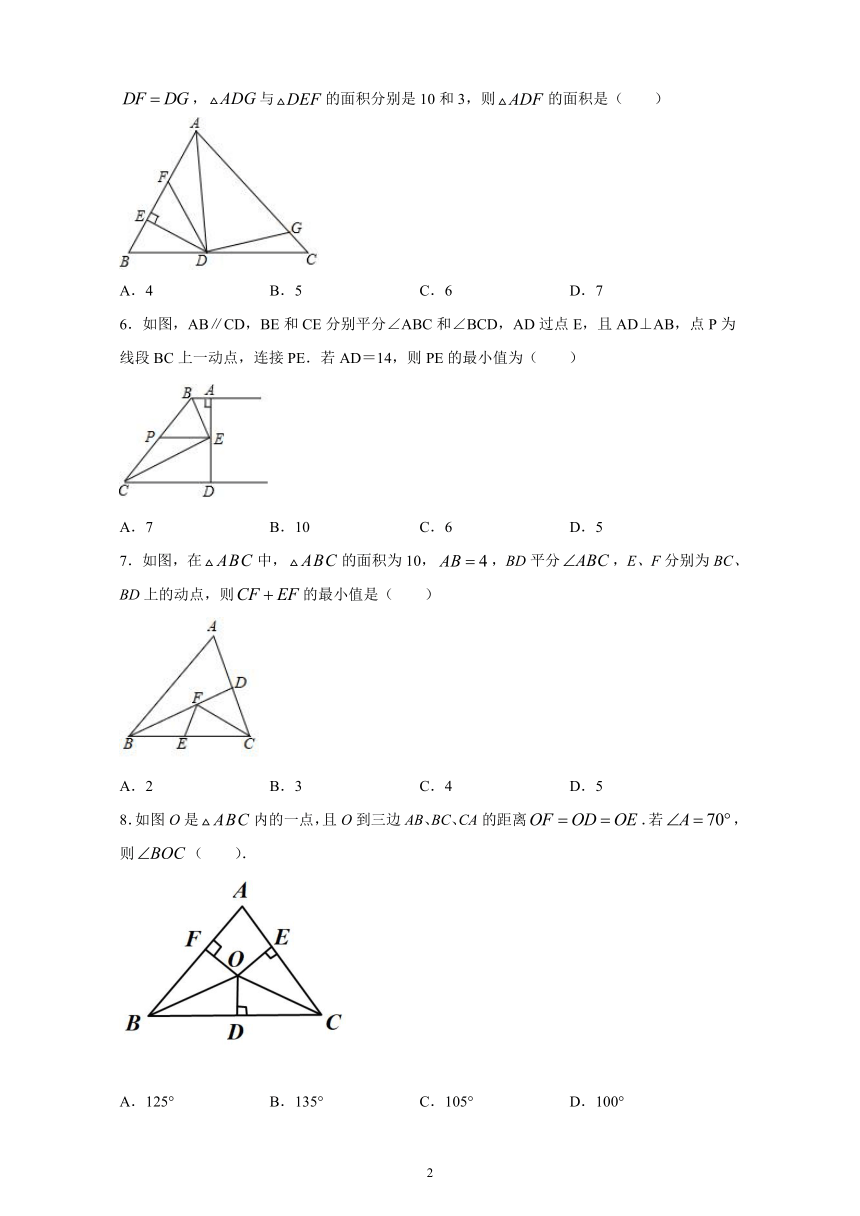
5.如图是的角平分线,于,点,分别是,上的点,且,与的面积分别是10和3,则的面积是(
)
A.4
B.5
C.6
D.7
6.如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且AD⊥AB,点P为线段BC上一动点,连接PE.若AD=14,则PE的最小值为(
)
A.7
B.10
C.6
D.5
7.如图,在中,的面积为10,,BD平分,E、F分别为BC、BD上的动点,则的最小值是(
)
A.2
B.3
C.4
D.5
8.如图O是内的一点,且O到三边AB、BC、CA的距离.若,则(
).
A.125°
B.135°
C.105°
D.100°
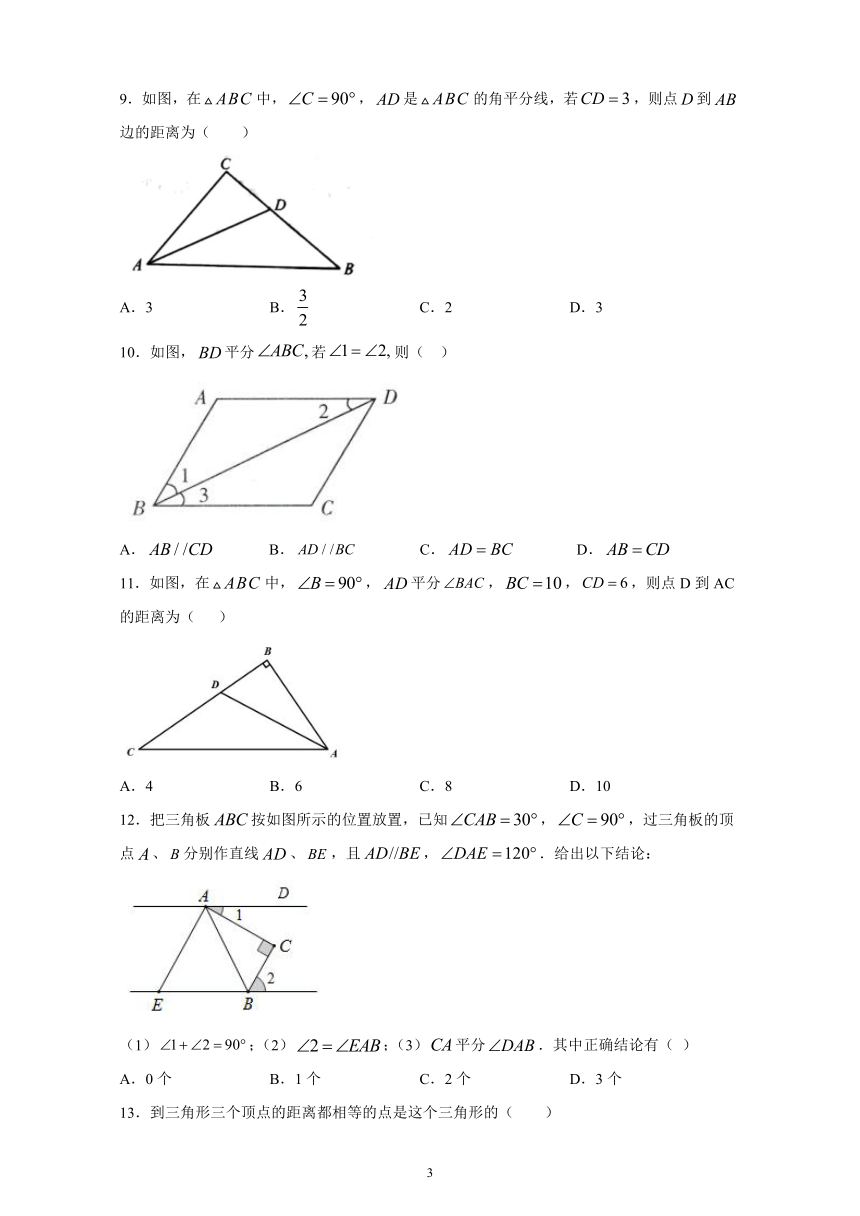
9.如图,在中,,是的角平分线,若,则点到边的距离为(
)
A.3
B.
C.2
D.3
10.如图,平分若则(
)
A.
B.
C.
D.
11.如图,在中,,平分,,,则点D到AC的距离为(
)
A.4
B.6
C.8
D.10
12.把三角板按如图所示的位置放置,已知,,过三角板的顶点、分别作直线、,且,.给出以下结论:
(1);(2);(3)平分.其中正确结论有(
)
A.0个
B.1个
C.2个
D.3个
13.到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条边的垂直平分线的交点
14.如图,已知,点O为与的平分线的交点,且于D.若,则四边形ABOC的面积是(
)
A.36
B.32
C.30
D.64
15.如图,是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有(
)处.
A.
B.
C.
D.
二、填空题
16.如图,OP平分∠AOB,PC⊥OA,点D是OB上的动点,若PC=1cm,则PD的长的最小值为
___.
17.如图,在中,为的平分线,于点,于点.若的面积是,,,则____.
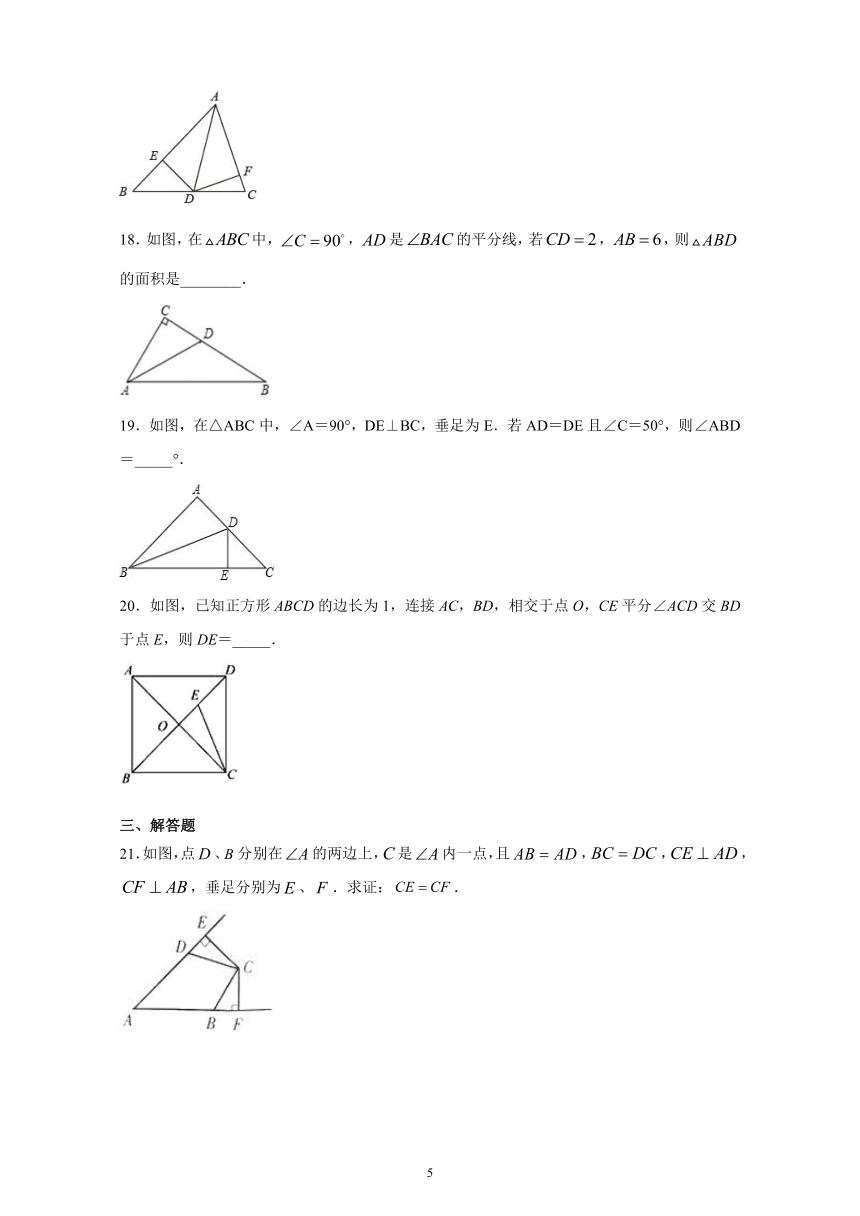
18.如图,在中,,是的平分线,若,,则的面积是________.
19.如图,在△ABC中,∠A=90°,DE⊥BC,垂足为E.若AD=DE且∠C=50°,则∠ABD=_____°.
20.如图,已知正方形ABCD的边长为1,连接AC,BD,相交于点O,CE平分∠ACD交BD于点E,则DE=_____.
三、解答题
21.如图,点、分别在的两边上,是内一点,且,,,,垂足分别为、.求证:.
22.如图,,是上一点,且平分,平分,求证:.
23.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,点F在AC上,且DF=BD.
(1)
求证:CF=BE
(2)
若AC=8,AB=10,且△ABC的面积等于24,求DE的长
24.如图所示,在四边形ABDC中,AD是∠BAC的平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且BD=CD.求证:∠C+∠ABD=180°.
参考答案
1.C
解:如图,∵BD+CD=BC=32,BD:DC=9:7,
∴CD=14,
作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD=14,(角平分线上的点到角的两边的距离相等)
即点D到AB的距离为14,
故选:C.
2.C
解:过点P作PF⊥AD,并延长FP
交BC于点G,
,
,
又的平分线与的平分线相交于点作于点,
PE=PF=PG,
,
GF=6.
故选:C.
3.A
解:由作法得平分,
过D作于E,则(角平分线上的点到角两边的距离相等),
∵,
∴,
故选:A.
4.B
解:∵AD平分∠BAC,EFAC,
∴,
∴AF=EF,
∵BE⊥AD,
∴,,
∴,
∴BF=EF,
∴AF=BF;
故答案选B.
5.A
解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC
∴DF=DH,
在Rt△DEF和Rt△DGH中,
,
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH=3,
同理Rt△ADF≌Rt△ADH,
∴S△ADF=S△ADH=
∴S△AED=
,
故选:A.
6.A
解:当EP⊥BC时,EP最短,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,
∵BE平分∠ABC,AE⊥AB,EP⊥BC,
∴EP=EA,
同理,EP=ED,
此时,EP=AD=×14=7,
故选A.
7.D
解:过点作于点,交于点,过点作于,
平分,于点,于,
,
的最小值.
三角形的面积为10,,
,
.
即的最小值为5,
故选:D.
8.A
解:∵O到三边AB、BC、CA的距离OF=OD=OE,
∴点O是三角形三条角平分线的交点,
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×110°=55°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
故选:A.
9.A
解:∵AD是的角平分线,
∴点D到AB边的距离等于CD=3.
故选:A.
10.B
解:∵平分,
,
,
,
,
故选:B.
11.A
解:∵BC=10,CD=6,
∴BD=4.
∵∠B=90°,AD平分∠BAC
.
由角平分线的性质,得点D到AC的距离等于BD=4.
故选:A.
12.C
解:∵,
∴.
∵.
∴,故(1)正确.
∵,
∵,
∴.故(2)正确.
∵,
∴的大小随的大小变化而变化,
∵固定,
∴CA不一定平分.故(3)错误.
综上,正确的结论有两个.
故选:C.
13.D
解:到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,
故选择:D.
14.B
解:过O作OE⊥AB于E,OF⊥AC于F,连接OA,
∵点O为∠ABC与∠ACB的平分线的交点,OD⊥BC于D,OD=4,
∴OE=OD=4,OF=OD=4,
∵AB+AC=16,
∴四边形ABOC的面积S=S△ABO+S△ACO=
=
=×(AB+AC)
=×16
=32,
故选:B.
15.D
解:(1)三角形两个内角平分线的交点,共一处
(2)三个外角两两平分线的交点,共三处,
共四处,
故选:D.
.
16.
解:垂线段最短,
当时最短,
是的平分线,,
,
,
,
即长度最小为1.
故答案为:.
17.2
解:在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∴S△ABC=S△ABD+S△ACD=AB?DE+AC?DF,
∵△ABC面积是28cm2,AB=20cm,AC=8cm,
∴×20DE+×8DF=10DE+4DF=14DE=28,
解得DE=2cm.
故答案为:2.
18.6
解:设点到的距离为,
是的平分线,,
,
故答案为:6
19.
解:
平分
故答案为:
20.
解:如图所示,过点E作于F,
∵正方形ABCD的边长为1,
∴AC=BD=,,
∴OA=OC=OB=OD=,
∵CE平分∠ACD交BD于点E,
∴EO=EF,
∵在正方形ABCD中,∠ADB=∠CDB=45°,
∴EF=DF,
设,则,
∵OD=OE+DE=,
∴解得,
∴DE=OD-OE=,
故答案为:.
21.见解析
证明:连接
,,
(全等三角形对应角相等)
又
,,
(角平分线上的点到角两边的距离相等).
22.见解析.
证明:如图:
过作于,
,平分,平分,
,,,,,,
在和中,
,
,
,
同理:AE=AB,
.
23.(1)见解析;(2)
(1)证明:∵AD平分∠CAB且DE⊥AB,DC⊥AC
∴DE=DC
在Rt△DCF和Rt△DEB中
∵
DE=DC,DF=BD
∴Rt△DCF≌Rt△DEB,
∴CF=BE;
(2)由(1)得:CD=DE,
∵S△ACB=S△ACD+S△ADB,
∴S△ABC=AC?CD+AB?DE,
又∵AC=8,AB=10,且△ABC的面积等于24,
∴,
∴.
24.见解析
证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△DFC和Rt△DEB中,
,
∴Rt△DFC≌Rt△DEB(HL),
∴∠C=∠DBE,
∵∠DBE+∠ABD=180°,
∴∠C+∠ABD=180°.
角的平分线的性质
一、单选题
1.在△ABC中,∠C=90°,角平分线AD交BC于点D,BC=32,BD:CD=9:7,则D点到AB边的距离为( )
A.18
B.16
C.14
D.12
2.如图,,的平分线与的平分线相交于点,作于,若,则两平行线与间的距离为(
)
A.
B.
C.
D.
3.如图,在中,,以顶点B为圆心,适当长度为半径画弧,分别交,BC于点M,N,再分别以点M,N为圆心,以大于的长为半径作弧,两弧相交于点P;作射线BP交AC于点D,若CD=4,则点D到的距离为( )
A.4
B.3
C.
D.1
4.如图,在△ABC中,AD平分∠BAC,过B点作BE⊥AD于E,过E作EFAC交AB于F,则(
)
A.不确定
B.AF=BF
C.AFBF
D.AFBF
5.如图是的角平分线,于,点,分别是,上的点,且,与的面积分别是10和3,则的面积是(
)
A.4
B.5
C.6
D.7
6.如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且AD⊥AB,点P为线段BC上一动点,连接PE.若AD=14,则PE的最小值为(
)
A.7
B.10
C.6
D.5
7.如图,在中,的面积为10,,BD平分,E、F分别为BC、BD上的动点,则的最小值是(
)
A.2
B.3
C.4
D.5
8.如图O是内的一点,且O到三边AB、BC、CA的距离.若,则(
).
A.125°
B.135°
C.105°
D.100°
9.如图,在中,,是的角平分线,若,则点到边的距离为(
)
A.3
B.
C.2
D.3
10.如图,平分若则(
)
A.
B.
C.
D.
11.如图,在中,,平分,,,则点D到AC的距离为(
)
A.4
B.6
C.8
D.10
12.把三角板按如图所示的位置放置,已知,,过三角板的顶点、分别作直线、,且,.给出以下结论:
(1);(2);(3)平分.其中正确结论有(
)
A.0个
B.1个
C.2个
D.3个
13.到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条边的垂直平分线的交点
14.如图,已知,点O为与的平分线的交点,且于D.若,则四边形ABOC的面积是(
)
A.36
B.32
C.30
D.64
15.如图,是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有(
)处.
A.
B.
C.
D.
二、填空题
16.如图,OP平分∠AOB,PC⊥OA,点D是OB上的动点,若PC=1cm,则PD的长的最小值为
___.
17.如图,在中,为的平分线,于点,于点.若的面积是,,,则____.
18.如图,在中,,是的平分线,若,,则的面积是________.
19.如图,在△ABC中,∠A=90°,DE⊥BC,垂足为E.若AD=DE且∠C=50°,则∠ABD=_____°.
20.如图,已知正方形ABCD的边长为1,连接AC,BD,相交于点O,CE平分∠ACD交BD于点E,则DE=_____.
三、解答题
21.如图,点、分别在的两边上,是内一点,且,,,,垂足分别为、.求证:.
22.如图,,是上一点,且平分,平分,求证:.
23.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,点F在AC上,且DF=BD.
(1)
求证:CF=BE
(2)
若AC=8,AB=10,且△ABC的面积等于24,求DE的长
24.如图所示,在四边形ABDC中,AD是∠BAC的平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且BD=CD.求证:∠C+∠ABD=180°.
参考答案
1.C
解:如图,∵BD+CD=BC=32,BD:DC=9:7,
∴CD=14,
作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD=14,(角平分线上的点到角的两边的距离相等)
即点D到AB的距离为14,
故选:C.
2.C
解:过点P作PF⊥AD,并延长FP
交BC于点G,
,
,
又的平分线与的平分线相交于点作于点,
PE=PF=PG,
,
GF=6.
故选:C.
3.A
解:由作法得平分,
过D作于E,则(角平分线上的点到角两边的距离相等),
∵,
∴,
故选:A.
4.B
解:∵AD平分∠BAC,EFAC,
∴,
∴AF=EF,
∵BE⊥AD,
∴,,
∴,
∴BF=EF,
∴AF=BF;
故答案选B.
5.A
解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC
∴DF=DH,
在Rt△DEF和Rt△DGH中,
,
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH=3,
同理Rt△ADF≌Rt△ADH,
∴S△ADF=S△ADH=
∴S△AED=
,
故选:A.
6.A
解:当EP⊥BC时,EP最短,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,
∵BE平分∠ABC,AE⊥AB,EP⊥BC,
∴EP=EA,
同理,EP=ED,
此时,EP=AD=×14=7,
故选A.
7.D
解:过点作于点,交于点,过点作于,
平分,于点,于,
,
的最小值.
三角形的面积为10,,
,
.
即的最小值为5,
故选:D.
8.A
解:∵O到三边AB、BC、CA的距离OF=OD=OE,
∴点O是三角形三条角平分线的交点,
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×110°=55°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
故选:A.
9.A
解:∵AD是的角平分线,
∴点D到AB边的距离等于CD=3.
故选:A.
10.B
解:∵平分,
,
,
,
,
故选:B.
11.A
解:∵BC=10,CD=6,
∴BD=4.
∵∠B=90°,AD平分∠BAC
.
由角平分线的性质,得点D到AC的距离等于BD=4.
故选:A.
12.C
解:∵,
∴.
∵.
∴,故(1)正确.
∵,
∵,
∴.故(2)正确.
∵,
∴的大小随的大小变化而变化,
∵固定,
∴CA不一定平分.故(3)错误.
综上,正确的结论有两个.
故选:C.
13.D
解:到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,
故选择:D.
14.B
解:过O作OE⊥AB于E,OF⊥AC于F,连接OA,
∵点O为∠ABC与∠ACB的平分线的交点,OD⊥BC于D,OD=4,
∴OE=OD=4,OF=OD=4,
∵AB+AC=16,
∴四边形ABOC的面积S=S△ABO+S△ACO=
=
=×(AB+AC)
=×16
=32,
故选:B.
15.D
解:(1)三角形两个内角平分线的交点,共一处
(2)三个外角两两平分线的交点,共三处,
共四处,
故选:D.
.
16.
解:垂线段最短,
当时最短,
是的平分线,,
,
,
,
即长度最小为1.
故答案为:.
17.2
解:在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∴S△ABC=S△ABD+S△ACD=AB?DE+AC?DF,
∵△ABC面积是28cm2,AB=20cm,AC=8cm,
∴×20DE+×8DF=10DE+4DF=14DE=28,
解得DE=2cm.
故答案为:2.
18.6
解:设点到的距离为,
是的平分线,,
,
故答案为:6
19.
解:
平分
故答案为:
20.
解:如图所示,过点E作于F,
∵正方形ABCD的边长为1,
∴AC=BD=,,
∴OA=OC=OB=OD=,
∵CE平分∠ACD交BD于点E,
∴EO=EF,
∵在正方形ABCD中,∠ADB=∠CDB=45°,
∴EF=DF,
设,则,
∵OD=OE+DE=,
∴解得,
∴DE=OD-OE=,
故答案为:.
21.见解析
证明:连接
,,
(全等三角形对应角相等)
又
,,
(角平分线上的点到角两边的距离相等).
22.见解析.
证明:如图:
过作于,
,平分,平分,
,,,,,,
在和中,
,
,
,
同理:AE=AB,
.
23.(1)见解析;(2)
(1)证明:∵AD平分∠CAB且DE⊥AB,DC⊥AC
∴DE=DC
在Rt△DCF和Rt△DEB中
∵
DE=DC,DF=BD
∴Rt△DCF≌Rt△DEB,
∴CF=BE;
(2)由(1)得:CD=DE,
∵S△ACB=S△ACD+S△ADB,
∴S△ABC=AC?CD+AB?DE,
又∵AC=8,AB=10,且△ABC的面积等于24,
∴,
∴.
24.见解析
证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△DFC和Rt△DEB中,
,
∴Rt△DFC≌Rt△DEB(HL),
∴∠C=∠DBE,
∵∠DBE+∠ABD=180°,
∴∠C+∠ABD=180°.
