2021-2022学年华东师大新版八年级上册数学《第14章 勾股定理》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大新版八年级上册数学《第14章 勾股定理》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 266.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览




文档简介
2021-2022学年华东师大新版八年级上册数学《第14章
勾股定理》单元测试卷
一.选择题
1.下列几组数中,能作为直角三角形三边长度的是( )
A.2,3,4
B.4,5,6
C.6,8,11
D.5,12,13
2.已知△ABC中,∠B≠∠C,求证:AB≠AC.若用反证法证这个结论,应首先假设( )
A.∠B=∠C
B.∠A=∠B
C.AB=AC
D.∠A=∠C
3.如图是我国一位古代数学家在注解《周髀算经》时给出的,曾被选为2002年在北京召开的国际数学家大会的会徽,它通过对图形的切割拼接,巧妙地证明了勾股定理这位伟大的数学家是( )
A.杨辉
B.刘徽
C.祖冲之
D.赵爽
4.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为( )
A.2
B.2.6
C.3
D.4
5.如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
A.313
B.144
C.169
D.25
6.如图,三个正方形围成一个直角三角形,64,400分别为所在正方形的面积,则图中字母所代表的正方形面积是( )
A.400+64
B.
C.400﹣64
D.4002﹣642
7.下列各组数据不是勾股数的是( )
A.2,3,4
B.3,4,5
C.5,12,13
D.6,8,10
8.用反证法证明命题“四边形中至少有一个角是钝角或直角”,应先假设( )
A.四边形中没有一个角是钝角或直角
B.四边形中至多有一个钝角或直角
C.四边形中没有一个角是锐角
D.四边形中没有一个角是钝角
9.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M为( )
A.2
B.﹣1
C.﹣1
D.
10.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2
B.a:b:c=5:12:13
C.∠A:∠B:∠C=3:4:5
D.∠C=∠A﹣∠B
二.填空题
11.若一个三角形的三边长分别为5、12、13,则此三角形的面积为
.
12.用反证法证明“如果|a|>a,那么a<0.”是真命题时,第一步应先假设
.
13.在直角三角形中,两边长分别为3和4,则最长边的长度为
.
14.若一直角三角形两直角边长分别为6和8,则斜边长为
.
15.已知:在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,则斜边AB=
,斜边AB上的高线长为
.
16.清代数学家梅文鼎在《勾股举隅》一书中,用四个全等的直角三角形拼出正方形ABDE的方法证明了勾股定理(如图),若Rt△ABC的斜边AB=5,BC=3,则图中线段CE的长为
.
17.如图,在Rt△ABC中,∠C=90°,BE,AF分别是∠ABC,∠CAB平分线,BE,AF交于点O,OM⊥AB,AB=10,AC=8,则OM=
.
18.三角形的三边长为a、b、c,且满足等式(a+b)2﹣c2=2ab,则此三角形是
三角形(直角、锐角、钝角).
19.若3,4,a和5,b,13是两组勾股数,则a+b的值是
.
20.用反证法证明“已知五个正数的和等于1,求证:这五个正数中至少有一个大于或等于”时,首先要假设
.
三.解答题
21.如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且∠ABC=90°,连接AC,试判断△ACD的形状.
22.利用勾股定理可以在数轴上画出表示的点,请依据以下思路完成画图,并保留画图痕迹:
第一步:(计算)尝试满足=,使其中a,b都为正整数,你取的正整数a=
,b=
;
第二步:(画长为的线段)以第一步中你所取的正整数a,b为两条直角边长画Rt△OEF,使O为原点,点E落在数轴的正半轴上,∠OEF=90°,则斜边OF的长即为.
请在下面的数轴上画图:(第二步不要求尺规作图,不要求写画法)
第三步:(画表示的点)在下面的数轴上画出表示的点M,并描述第三步的画图步骤:
.
23.我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:
(1)叙述勾股定理(用文字及符号语言叙述);
(2)证明勾股定理;
(3)若大正方形的面积是13,小正方形的面积是1,求(a+b)2的值.
24.如图,在Rt△ABD中,∠ABD=90°,AD=10,AB=8.在其右侧的同一个平面内作△BCD,使BC=8,CD=2.求证:AB∥DC.
25.如图1,△ABC中,CD⊥AB于D,且BD:AD:CD=2:3:4,
(1)试说明△ABC是等腰三角形;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
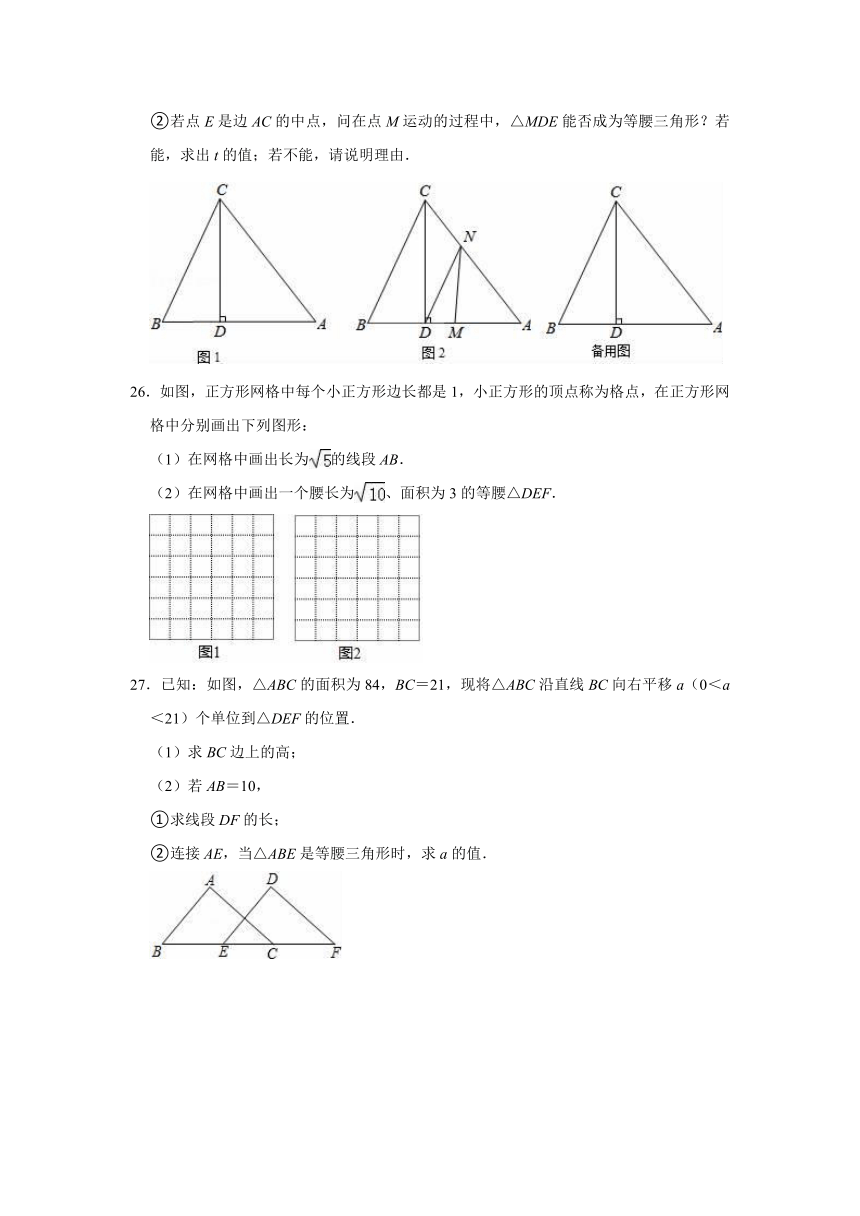
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.
26.如图,正方形网格中每个小正方形边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
(1)在网格中画出长为的线段AB.
(2)在网格中画出一个腰长为、面积为3的等腰△DEF.
27.已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连接AE,当△ABE是等腰三角形时,求a的值.
参考答案与试题解析
一.选择题
1.解:A、22+32≠42,故不是直角三角形,故错误;
B、42+52≠62,故不是直角三角形,故错误;
C、62+82≠112,故不是直角三角形,故错误;
D、52+122=132,故是直角三角形,故正确.
故选:D.
2.解:∵已知△ABC中,∠B≠∠C,求证:AB≠AC.
∴若用反证法证这个结论,应首先假设:AB=AC.
故选:C.
3.解:由题意,可知这位伟大的数学家是赵爽.
故选:D.
4.解:在Rt△ABC中,根据勾股定理,AB==13,
又∵AC=12,BC=5,AM=AC,BN=BC,
∴AM=12,BN=5,
∴MN=AM+BN﹣AB=12+5﹣13=4.
故选:D.
5.解:如图所示:
根据题意得:EF2=169,DF2=144,
在Rt△DEF中,由勾股定理得:
DE2=EF2﹣DF2=169﹣144=25,
即正方形A的面积为25;
故选:D.
6.解:根据勾股定理和正方形的面积公式,得M=400﹣64.
故选:C.
7.解:A、12+32≠42
,不能构成直角三角形,所以不是勾股数,故符合题意;
B、32+42=52,能构成直角三角形,所以是勾股数,故不符合题意;
C、52+122=132,能构成直角三角形,所以是勾股数,故不符合题意;
D、62+82=102,能构成直角三角形,所以是勾股数,故不符合题意;
故选:A.
8.解:用反证法证明“四边形中至少有一个角是钝角或直角”时第一步应假设:四边形中没有一个角是钝角或直角.
故选:A.
9.解:由题意得AC===,
故AM=,BM=AM﹣AB=﹣3,
又∵点B表示的数为2,
∴点M表示的数为﹣1.
故选:C.
10.解:A、由b2﹣c2=a2,可得:b2=c2+a2,是直角三角形,故本选项错误;
B、由a:b:c=5:12:13,可得(5x)2+(12x)2=(13x)2,是直角三角形,故本选项错误;
C、由∠A:∠B:∠C=3:4:5,可得:∠C=75°,不是直角三角形,故选项正确;
D、由∠C=∠A﹣∠B,可得∠A=90°,是直角三角形,故本选项错误;
故选:C.
二.填空题
11.解:∵52+122=132,
∴三边长分别为5、12、13的三角形构成直角三角形,其中的直角边是5、12,
∴此三角形的面积为×5×12=30.
12.解:用反证法证明“如果|a|>a,那么a<0.”是真命题时,第一步应先假设:a≥0.
故答案为:a≥0.
13.解:①当4为斜边时,此时最长边为4.
②当4是直角边时,斜边==5,此时最长边为5.
故答案是:4或5.
14.解:在直角三角形中,斜边的平方等于两条直角边平方和,
故斜边长==10,
故答案为
10.
15.解:根据勾股定理,得:AB==10,
三角形的面积是×6×8=24,
AB边上的高为=4.8,
故答案为10,4.8
16.解:在Rt△ABC中,AC==4,
∵Rt△ACB≌Rt△EFA,
∴AF=BC=3,EF=AC=4,
∴FC=AC﹣AF=1,
∴CE==,
故答案为:.
17.解:过O作OG⊥AC于G,OH⊥BC于H,连接OC,
∵AF平分∠CAB,BE平分∠ABC,
∴OG=OH=OM,
∵∠C=90°,AB=10,AC=8,
∴BC==6
∴S△ABC=AC?BC=×AB?OM+AC?OG+BC?OH,
∴×8×6=+×8×OG+,
∴OM=2,
故答案为:2.
18.解:∵(a+b)2﹣c2=2ab,
∴a2+2ab+b2﹣c2=2ab,
∴a2+b2=c2,
∴三角形是直角三角形.
故答案为直角.
19.解:∵3,4,a和5,b,13是两组勾股数,
∴a=5,b=12,
∴a+b=17,
故答案为:17.
20.解:首先要假设这五个数都小于.
故答案为:这五个数都小于.
三.解答题
21.解:△ACD是直角三角形.理由是:
∵∠B=90°,AB=1,BC=2,
∴AC2=AB2+BC2=1+4=5,
∴AC=,
又∵AC2+CD2=5+4=9,AD2=9,
∴AC2+CD2=AD2,
∴△ACD是直角三角形.
22.解:第一步:a=4,b=2;
第二步:如图,OF为所作;
第三步:如图,以原点为圆心,OF为半径画弧交数轴的正半轴于点M,则点M为所作.
故答案为4,2;以原点为圆心,OF为半径画弧交数轴的正半轴于点M,则点M为所作.
23.解:(1)勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中,两条直角边分别为a、b,斜边为c,a2+b2=c2.
(2)∵S大正方形=c2,S小正方形=(b﹣a)2,4SRt△=4×ab=2ab,
∴c2=2ab+(b﹣a)2=2ab+b2﹣2ab+a2=a2+b2,
即a2+b2=c2.
(3)∵4SRt△=S大正方形﹣S小正方形=13﹣1=12,
∴2ab=12.
∴(a+b)2
=a2+b2+2ab
=c2+2ab
=13+12
=25.
24.证明:∵在Rt△ABD中,∠ABD=90°,AD=10,AB=8,
∴BD===6,
∵BC=8,CD=2,
∴62+(2)2=82,
∴△BDC是直角三角形,
∴∠BDC=90°,
∴∠ABD=∠BDC,
∴AB∥DC.
25.(1)证明:设BD=2x,AD=3x,CD=4x,
则AB=5x,
在Rt△ACD中,AC==5x,
∴AB=AC,
∴△ABC是等腰三角形;
(2)解:S△ABC=×5x×4x=40cm2,而x>0,
∴x=2cm,
则BD=4cm,AD=6cm,CD=8cm,AC=10cm.
①当MN∥BC时,AM=AN,
即10﹣t=t,
∴t=5;
当DN∥BC时,AD=AN,
得:t=6;
∴若△DMN的边与BC平行时,t值为5或6.
②∵点E是边AC的中点,CD⊥AB,
∴DE=AC=5,
当点M在BD上,即0≤t<4时,△MDE为钝角三角形,但DM≠DE;
当t=4时,点M运动到点D,不构成三角形
当点M在DA上,即4<t≤10时,△MDE为等腰三角形,有3种可能.
如果DE=DM,则t﹣4=5,
∴t=9;
如果ED=EM,则点M运动到点A,
∴t=10;
如果MD=ME=t﹣4,
过点E作EF⊥AB于F,如图3所示:
∵ED=EA,
∴DF=AF=AD=3,
在Rt△AEF中,EF=4;
∵BM=t,BF=7,
∴FM=t﹣7
则在Rt△EFM中,(t﹣4)2﹣(t﹣7)2=42,
∴t=.
综上所述,符合要求的t值为9或10或.
26.解:(1)如图所示:线段AB即为所求;
(2)△DEF即为所求.
27.解:(1)作AM⊥BC于M,
∵△ABC的面积为84,
∴×BC×AM=84,
解得,AM=8,即BC边上的高为8;
(2)①在Rt△ABM中,BM==6,
∴CM=BC﹣BM=15,
在Rt△ACM中,AC==17,
由平移的性质可知,DF=AC=17;
②当AB=BE=10时,a=BE=10;
当AB=AE=10时,BE=2BM=12,
则a=BE=12;
当EA=EB=a时,ME=a﹣6,
在Rt△AME中,AM2+ME2=AE2,
即82+(a﹣6)2=a2,
解得,a=,
则当△ABE是等腰三角形时,a的值为10或12或.
勾股定理》单元测试卷
一.选择题
1.下列几组数中,能作为直角三角形三边长度的是( )
A.2,3,4
B.4,5,6
C.6,8,11
D.5,12,13
2.已知△ABC中,∠B≠∠C,求证:AB≠AC.若用反证法证这个结论,应首先假设( )
A.∠B=∠C
B.∠A=∠B
C.AB=AC
D.∠A=∠C
3.如图是我国一位古代数学家在注解《周髀算经》时给出的,曾被选为2002年在北京召开的国际数学家大会的会徽,它通过对图形的切割拼接,巧妙地证明了勾股定理这位伟大的数学家是( )
A.杨辉
B.刘徽
C.祖冲之
D.赵爽
4.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为( )
A.2
B.2.6
C.3
D.4
5.如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
A.313
B.144
C.169
D.25
6.如图,三个正方形围成一个直角三角形,64,400分别为所在正方形的面积,则图中字母所代表的正方形面积是( )
A.400+64
B.
C.400﹣64
D.4002﹣642
7.下列各组数据不是勾股数的是( )
A.2,3,4
B.3,4,5
C.5,12,13
D.6,8,10
8.用反证法证明命题“四边形中至少有一个角是钝角或直角”,应先假设( )
A.四边形中没有一个角是钝角或直角
B.四边形中至多有一个钝角或直角
C.四边形中没有一个角是锐角
D.四边形中没有一个角是钝角
9.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M为( )
A.2
B.﹣1
C.﹣1
D.
10.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2
B.a:b:c=5:12:13
C.∠A:∠B:∠C=3:4:5
D.∠C=∠A﹣∠B
二.填空题
11.若一个三角形的三边长分别为5、12、13,则此三角形的面积为
.
12.用反证法证明“如果|a|>a,那么a<0.”是真命题时,第一步应先假设
.
13.在直角三角形中,两边长分别为3和4,则最长边的长度为
.
14.若一直角三角形两直角边长分别为6和8,则斜边长为
.
15.已知:在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,则斜边AB=
,斜边AB上的高线长为
.
16.清代数学家梅文鼎在《勾股举隅》一书中,用四个全等的直角三角形拼出正方形ABDE的方法证明了勾股定理(如图),若Rt△ABC的斜边AB=5,BC=3,则图中线段CE的长为
.
17.如图,在Rt△ABC中,∠C=90°,BE,AF分别是∠ABC,∠CAB平分线,BE,AF交于点O,OM⊥AB,AB=10,AC=8,则OM=
.
18.三角形的三边长为a、b、c,且满足等式(a+b)2﹣c2=2ab,则此三角形是
三角形(直角、锐角、钝角).
19.若3,4,a和5,b,13是两组勾股数,则a+b的值是
.
20.用反证法证明“已知五个正数的和等于1,求证:这五个正数中至少有一个大于或等于”时,首先要假设
.
三.解答题
21.如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且∠ABC=90°,连接AC,试判断△ACD的形状.
22.利用勾股定理可以在数轴上画出表示的点,请依据以下思路完成画图,并保留画图痕迹:
第一步:(计算)尝试满足=,使其中a,b都为正整数,你取的正整数a=
,b=
;
第二步:(画长为的线段)以第一步中你所取的正整数a,b为两条直角边长画Rt△OEF,使O为原点,点E落在数轴的正半轴上,∠OEF=90°,则斜边OF的长即为.
请在下面的数轴上画图:(第二步不要求尺规作图,不要求写画法)
第三步:(画表示的点)在下面的数轴上画出表示的点M,并描述第三步的画图步骤:
.
23.我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:
(1)叙述勾股定理(用文字及符号语言叙述);
(2)证明勾股定理;
(3)若大正方形的面积是13,小正方形的面积是1,求(a+b)2的值.
24.如图,在Rt△ABD中,∠ABD=90°,AD=10,AB=8.在其右侧的同一个平面内作△BCD,使BC=8,CD=2.求证:AB∥DC.
25.如图1,△ABC中,CD⊥AB于D,且BD:AD:CD=2:3:4,
(1)试说明△ABC是等腰三角形;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.
26.如图,正方形网格中每个小正方形边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
(1)在网格中画出长为的线段AB.
(2)在网格中画出一个腰长为、面积为3的等腰△DEF.
27.已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连接AE,当△ABE是等腰三角形时,求a的值.
参考答案与试题解析
一.选择题
1.解:A、22+32≠42,故不是直角三角形,故错误;
B、42+52≠62,故不是直角三角形,故错误;
C、62+82≠112,故不是直角三角形,故错误;
D、52+122=132,故是直角三角形,故正确.
故选:D.
2.解:∵已知△ABC中,∠B≠∠C,求证:AB≠AC.
∴若用反证法证这个结论,应首先假设:AB=AC.
故选:C.
3.解:由题意,可知这位伟大的数学家是赵爽.
故选:D.
4.解:在Rt△ABC中,根据勾股定理,AB==13,
又∵AC=12,BC=5,AM=AC,BN=BC,
∴AM=12,BN=5,
∴MN=AM+BN﹣AB=12+5﹣13=4.
故选:D.
5.解:如图所示:
根据题意得:EF2=169,DF2=144,
在Rt△DEF中,由勾股定理得:
DE2=EF2﹣DF2=169﹣144=25,
即正方形A的面积为25;
故选:D.
6.解:根据勾股定理和正方形的面积公式,得M=400﹣64.
故选:C.
7.解:A、12+32≠42
,不能构成直角三角形,所以不是勾股数,故符合题意;
B、32+42=52,能构成直角三角形,所以是勾股数,故不符合题意;
C、52+122=132,能构成直角三角形,所以是勾股数,故不符合题意;
D、62+82=102,能构成直角三角形,所以是勾股数,故不符合题意;
故选:A.
8.解:用反证法证明“四边形中至少有一个角是钝角或直角”时第一步应假设:四边形中没有一个角是钝角或直角.
故选:A.
9.解:由题意得AC===,
故AM=,BM=AM﹣AB=﹣3,
又∵点B表示的数为2,
∴点M表示的数为﹣1.
故选:C.
10.解:A、由b2﹣c2=a2,可得:b2=c2+a2,是直角三角形,故本选项错误;
B、由a:b:c=5:12:13,可得(5x)2+(12x)2=(13x)2,是直角三角形,故本选项错误;
C、由∠A:∠B:∠C=3:4:5,可得:∠C=75°,不是直角三角形,故选项正确;
D、由∠C=∠A﹣∠B,可得∠A=90°,是直角三角形,故本选项错误;
故选:C.
二.填空题
11.解:∵52+122=132,
∴三边长分别为5、12、13的三角形构成直角三角形,其中的直角边是5、12,
∴此三角形的面积为×5×12=30.
12.解:用反证法证明“如果|a|>a,那么a<0.”是真命题时,第一步应先假设:a≥0.
故答案为:a≥0.
13.解:①当4为斜边时,此时最长边为4.
②当4是直角边时,斜边==5,此时最长边为5.
故答案是:4或5.
14.解:在直角三角形中,斜边的平方等于两条直角边平方和,
故斜边长==10,
故答案为
10.
15.解:根据勾股定理,得:AB==10,
三角形的面积是×6×8=24,
AB边上的高为=4.8,
故答案为10,4.8
16.解:在Rt△ABC中,AC==4,
∵Rt△ACB≌Rt△EFA,
∴AF=BC=3,EF=AC=4,
∴FC=AC﹣AF=1,
∴CE==,
故答案为:.
17.解:过O作OG⊥AC于G,OH⊥BC于H,连接OC,
∵AF平分∠CAB,BE平分∠ABC,
∴OG=OH=OM,
∵∠C=90°,AB=10,AC=8,
∴BC==6
∴S△ABC=AC?BC=×AB?OM+AC?OG+BC?OH,
∴×8×6=+×8×OG+,
∴OM=2,
故答案为:2.
18.解:∵(a+b)2﹣c2=2ab,
∴a2+2ab+b2﹣c2=2ab,
∴a2+b2=c2,
∴三角形是直角三角形.
故答案为直角.
19.解:∵3,4,a和5,b,13是两组勾股数,
∴a=5,b=12,
∴a+b=17,
故答案为:17.
20.解:首先要假设这五个数都小于.
故答案为:这五个数都小于.
三.解答题
21.解:△ACD是直角三角形.理由是:
∵∠B=90°,AB=1,BC=2,
∴AC2=AB2+BC2=1+4=5,
∴AC=,
又∵AC2+CD2=5+4=9,AD2=9,
∴AC2+CD2=AD2,
∴△ACD是直角三角形.
22.解:第一步:a=4,b=2;
第二步:如图,OF为所作;
第三步:如图,以原点为圆心,OF为半径画弧交数轴的正半轴于点M,则点M为所作.
故答案为4,2;以原点为圆心,OF为半径画弧交数轴的正半轴于点M,则点M为所作.
23.解:(1)勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中,两条直角边分别为a、b,斜边为c,a2+b2=c2.
(2)∵S大正方形=c2,S小正方形=(b﹣a)2,4SRt△=4×ab=2ab,
∴c2=2ab+(b﹣a)2=2ab+b2﹣2ab+a2=a2+b2,
即a2+b2=c2.
(3)∵4SRt△=S大正方形﹣S小正方形=13﹣1=12,
∴2ab=12.
∴(a+b)2
=a2+b2+2ab
=c2+2ab
=13+12
=25.
24.证明:∵在Rt△ABD中,∠ABD=90°,AD=10,AB=8,
∴BD===6,
∵BC=8,CD=2,
∴62+(2)2=82,
∴△BDC是直角三角形,
∴∠BDC=90°,
∴∠ABD=∠BDC,
∴AB∥DC.
25.(1)证明:设BD=2x,AD=3x,CD=4x,
则AB=5x,
在Rt△ACD中,AC==5x,
∴AB=AC,
∴△ABC是等腰三角形;
(2)解:S△ABC=×5x×4x=40cm2,而x>0,
∴x=2cm,
则BD=4cm,AD=6cm,CD=8cm,AC=10cm.
①当MN∥BC时,AM=AN,
即10﹣t=t,
∴t=5;
当DN∥BC时,AD=AN,
得:t=6;
∴若△DMN的边与BC平行时,t值为5或6.
②∵点E是边AC的中点,CD⊥AB,
∴DE=AC=5,
当点M在BD上,即0≤t<4时,△MDE为钝角三角形,但DM≠DE;
当t=4时,点M运动到点D,不构成三角形
当点M在DA上,即4<t≤10时,△MDE为等腰三角形,有3种可能.
如果DE=DM,则t﹣4=5,
∴t=9;
如果ED=EM,则点M运动到点A,
∴t=10;
如果MD=ME=t﹣4,
过点E作EF⊥AB于F,如图3所示:
∵ED=EA,
∴DF=AF=AD=3,
在Rt△AEF中,EF=4;
∵BM=t,BF=7,
∴FM=t﹣7
则在Rt△EFM中,(t﹣4)2﹣(t﹣7)2=42,
∴t=.
综上所述,符合要求的t值为9或10或.
26.解:(1)如图所示:线段AB即为所求;
(2)△DEF即为所求.
27.解:(1)作AM⊥BC于M,
∵△ABC的面积为84,
∴×BC×AM=84,
解得,AM=8,即BC边上的高为8;
(2)①在Rt△ABM中,BM==6,
∴CM=BC﹣BM=15,
在Rt△ACM中,AC==17,
由平移的性质可知,DF=AC=17;
②当AB=BE=10时,a=BE=10;
当AB=AE=10时,BE=2BM=12,
则a=BE=12;
当EA=EB=a时,ME=a﹣6,
在Rt△AME中,AM2+ME2=AE2,
即82+(a﹣6)2=a2,
解得,a=,
则当△ABE是等腰三角形时,a的值为10或12或.
