2021-2022学年华东师大新版九年级上册数学《第24章 解直角三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大新版九年级上册数学《第24章 解直角三角形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 278.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 20:51:44 | ||
图片预览


文档简介
2021-2022学年华东师大新版九年级上册数学《第24章
解直角三角形》单元测试卷
一.选择题
1.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
A.AC2=AD?AB
B.CD2=CA?CB
C.CD2=AD?DB
D.BC2=BD?BA
2.如图,在Rt△ABC,∠BAC=90°,AD⊥BC,AB=10,BD=6,则BC的值为( )
A.
B.
C.
D.
3.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A﹣∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
4.如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
A.图中有三个直角三角形
B.∠1=∠2
C.∠1和∠B都是∠A的余角
D.∠2=∠A
5.在△ABC中,已知∠C=90°,AB=13,BC=5,则cosA的值是( )
A.
B.
C.
D.
6.如图,在Rt△ABC中,∠C=90°,如果AC=5,AB=13,那么cosA的值为( )
A.
B.
C.
D.
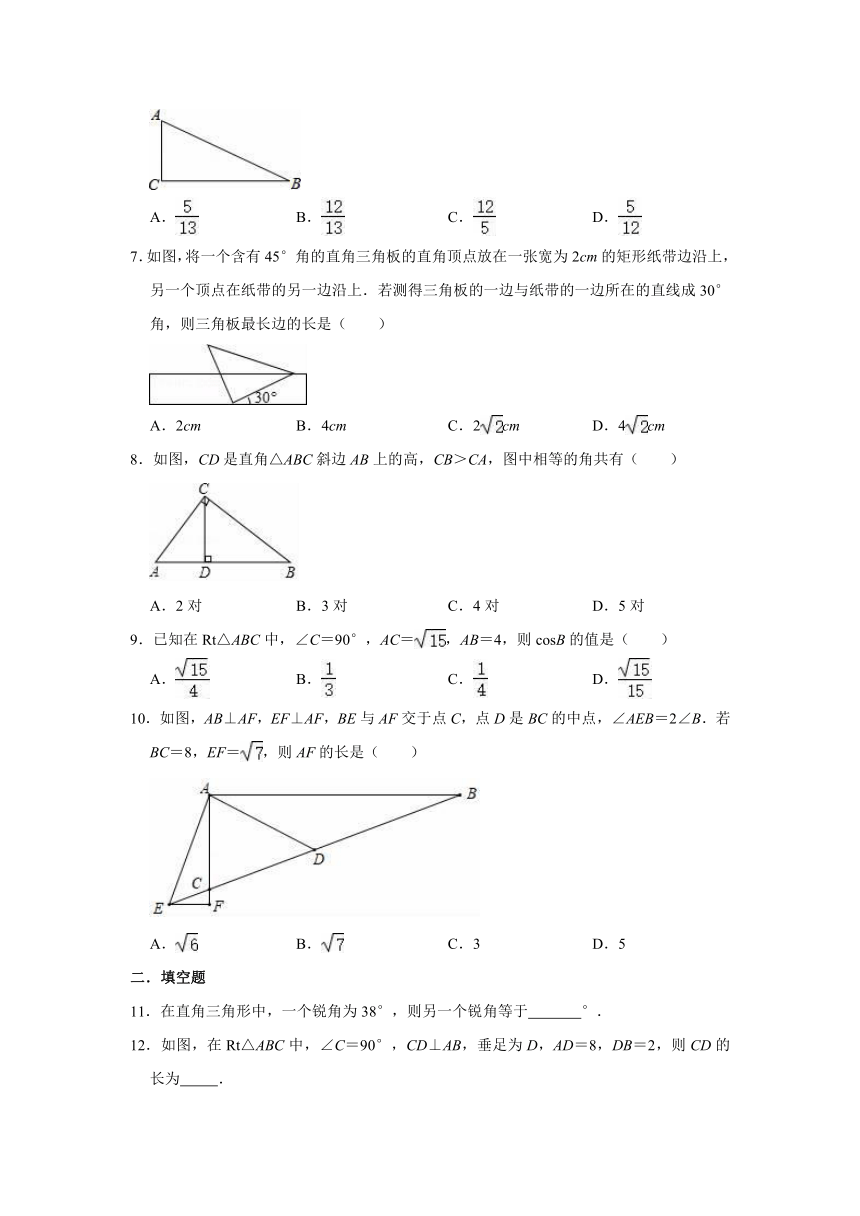
7.如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
A.2cm
B.4cm
C.2cm
D.4cm
8.如图,CD是直角△ABC斜边AB上的高,CB>CA,图中相等的角共有( )
A.2对
B.3对
C.4对
D.5对
9.已知在Rt△ABC中,∠C=90°,AC=,AB=4,则cosB的值是( )
A.
B.
C.
D.
10.如图,AB⊥AF,EF⊥AF,BE与AF交于点C,点D是BC的中点,∠AEB=2∠B.若BC=8,EF=,则AF的长是( )
A.
B.
C.3
D.5
二.填空题
11.在直角三角形中,一个锐角为38°,则另一个锐角等于
°.
12.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为
.
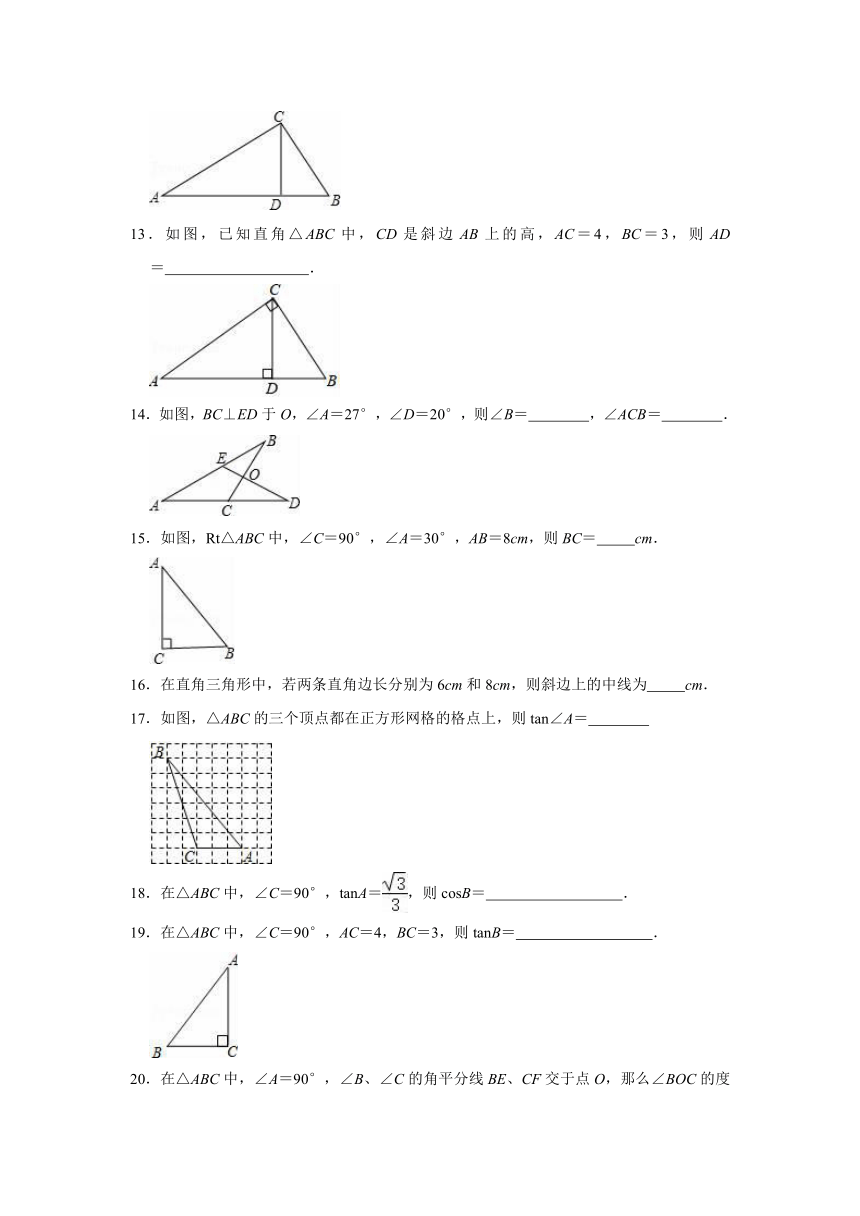
13.如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=
.
14.如图,BC⊥ED于O,∠A=27°,∠D=20°,则∠B=
,∠ACB=
.
15.如图,Rt△ABC中,∠C=90°,∠A=30°,AB=8cm,则BC=
cm.
16.在直角三角形中,若两条直角边长分别为6cm和8cm,则斜边上的中线为
cm.
17.如图,△ABC的三个顶点都在正方形网格的格点上,则tan∠A=
18.在△ABC中,∠C=90°,tanA=,则cosB=
.
19.在△ABC中,∠C=90°,AC=4,BC=3,则tanB=
.
20.在△ABC中,∠A=90°,∠B、∠C的角平分线BE、CF交于点O,那么∠BOC的度数是
.
三.解答题
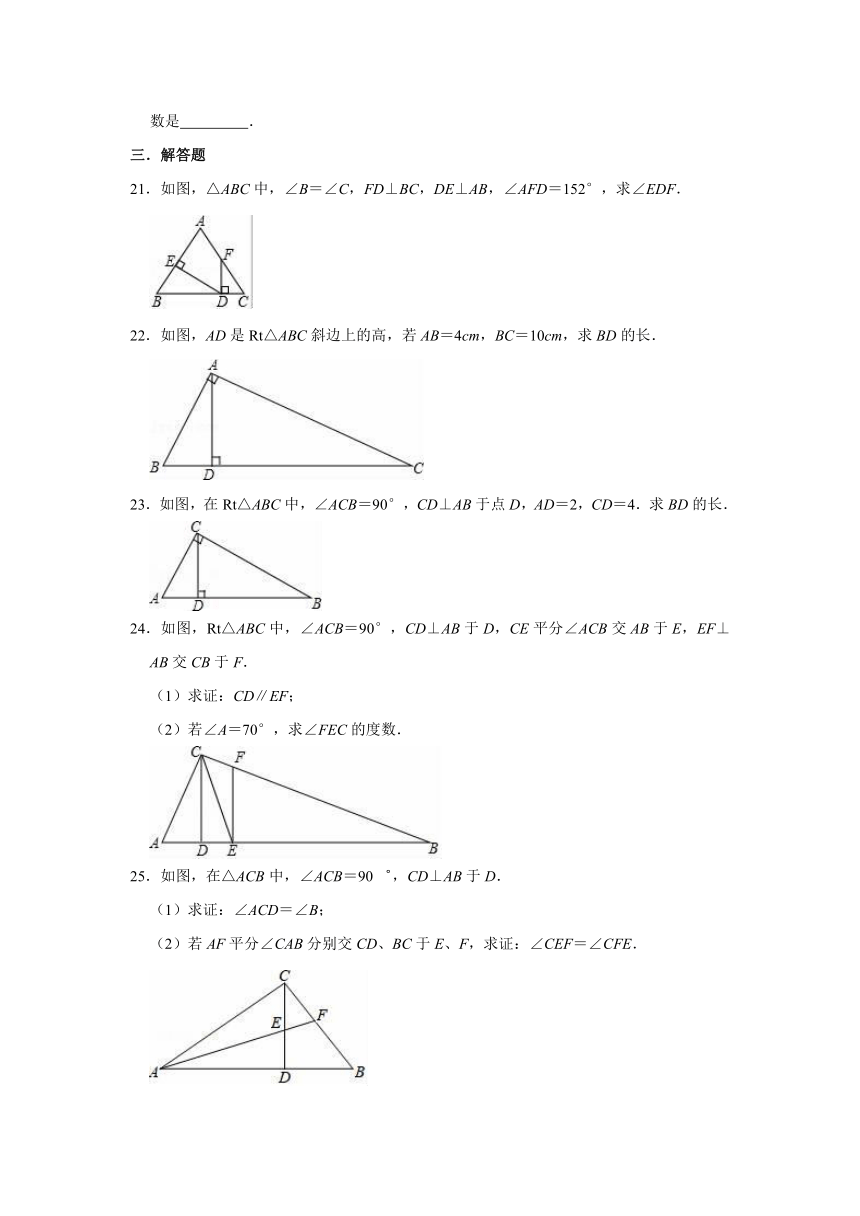
21.如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠EDF.
22.如图,AD是Rt△ABC斜边上的高,若AB=4cm,BC=10cm,求BD的长.
23.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.求BD的长.
24.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)求证:CD∥EF;
(2)若∠A=70°,求∠FEC的度数.
25.如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
26.已知:如图,△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,点E在AB的延长线上,∠E=45°,若AB=8,求BE的长.
27.如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.
(1)求证:ME=MF;
(2)若∠A=50°,求∠FME的度数.
参考答案与试题解析
一.选择题
1.解:∵∠ACB=90°,CD⊥AB于点D,
∴AC2=AD?AB,CD2=DA?DB,BC2=BD?BA.
故选:B.
2.解:根据射影定理得:AB2=BD×BC,
∴BC==.
故选:D.
3.解:A选项,∠A+∠B=∠C,即2∠C=180°,∠C=90°,为直角三角形,不符合题意;
B选项,∠A﹣∠B=∠C,即2∠A=180°,∠A=90°,为直角三角形,不符合题意;
C选项,∠A:∠B:∠C=1:2:3,即∠A+∠B=∠C,同A选项,不符合题意;
D选项,∠A=∠B=3∠C,即7∠C=180°,三个角没有90°角,故不是直角三角形,符合题意.
故选:D.
4.解:∵∠ACB=90°,CD⊥AB,垂足为D,
∴△ACD∽△CBD∽△ABC.
A、∵图中有三个直角三角形Rt△ACD、Rt△CBD、Rt△ABC;故本选项正确;
B、应为∠1=∠B、∠2=∠A;故本选项错误;
C、∵∠1=∠B、∠2=∠A,而∠B是∠A的余角,∴∠1和∠B都是∠A的余角;故本选项正确;
D、∵∠2=∠A;故本选项正确.
故选:B.
5.解:∵∠C=90°,AB=13,BC=5,
∴AC==12,
∴cosA==,
故选:D.
6.解:∵∠C=90°,AC=5,AB=13,
∴cosA==,
故选:A.
7.解:过点C作CD⊥AD,∴CD=2,
在直角三角形ADC中,
∵∠CAD=30°,
∴AC=2CD=2×2=4,
又∵三角板是有45°角的三角板,
∴AB=AC=4,
∴BC2=AB2+AC2=42+42=32,
∴BC=4,
故选:D.
8.解:∵CD是直角△ABC斜边AB上的高,
∴∠ACB=∠ADC=∠CDB=90°,
∴∠A+∠ACD=∠ACD+∠DCB=90°,
∴∠A=∠DCB,
同理得:∠B=∠ACD,
∴相等的角一共有5对,
故选:D.
9.解:如图:
∵∠C=90°,AC=,AB=4,
∴BC===1,
∴cosB==,
故选:C.
10.解:∵AB⊥AF,
∴∠FAB=90°,
∵点D是BC的中点,
∴AD=BD=BC,
∴∠DAB=∠B,
∴∠ADE=∠B+∠BAD=2∠B,
∵∠AEB=2∠B,
∴∠AED=∠ADE,
∴AE=AD,
∵BC=8,
∴AE=AD=4,
∵EF=,EF⊥AF,
∴AF===3,
故选:C.
二.填空题
11.解:在直角三角形中,一个锐角为38°,则另一个锐角等于90°﹣38°=52°.
故答案为52.
12.解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,
∴CD2=AD?BD=8×2,
则CD=4.
故答案是:4.
13.解:在Rt△ABC中,AB==5,
由射影定理得,AC2=AD?AB,
∴AD==,
故答案为:.
14.解:∵∠A=27°,∠D=20°,
∴∠BEO=∠A+∠D=27°+20°=47°,
∵BC⊥ED,
∴∠B=90°﹣∠BEO=90°﹣47°=43°;
在Rt△COD中,∠ACB=∠D+∠COD=20°+90°=110°.
故答案为:43°;110°.
15.解:根据含30度角的直角三角形的性质可知:BC=AB=4cm.
故答案为:4.
16.解:根据勾股定理得,斜边==10cm,
∴斜边上的中线=×斜边=×10=5cm.
故答案为:5.
17.解:作BE⊥AC于E,则BE=6,AE=5,
∴tan∠A===1.2
故答案为1.2.
18.解:法一:
利用三角函数的定义及勾股定理求解.
∵在Rt△ABC中,∠C=90°,tanA=,
设a=x,b=3x,则c=2x,
∴cosB==.
法二:
利用特殊角的三角函数值求解.
∵tanA=
∴∠A=30°,
∵∠C=90°
∴∠B=60°,
∴cosB=cos60°=.
故答案为:.
19.解:△ABC中,∠C=90°,AC=4,BC=3,
∴AB==5.
∴tanB==.
20.解:∵∠A=90°,
∴∠ABC+∠ACB=90°,
∵角平分线BE、CF交于点O,
∴∠OBC+∠OCB=45°,
∴∠BOC=180°﹣45°=135°.
故答案为135°.
三.解答题
21.解:∵∠AFD=152°,
∴∠DFC=28°,
∴∠B=∠C,FD⊥BC,DE⊥AB,
∴∠EDB=∠DFC=28°,
∴∠EDF=180°﹣∠EDB﹣∠FDC=180°﹣90°﹣28°=62°.
22.解:由射影定理得,AB2=BD?BC,
则BD==1.6.
23.解:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠CDB=∠ACB=90°,
∴∠ACD+∠BCD=90°,∠BCD+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴=,
∵AD=2,CD=4,
∴=,
∴BD=8.
24.(1)证明:∵CD⊥AB,EF⊥AB,
∴CD∥EF;
(2)解:∵CD⊥AB,
∴∠ACD=90°﹣70°=20°,
∵∠ACB=90°,CE平分∠ACB,
∴∠ACE=45°,
∴∠DCE=45°﹣20°=25°,
∵CD∥EF,
∴∠FEC=∠DCE=25°.
25.证明:(1)∵∠ACB=90゜,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B;
(2)在Rt△AFC中,∠CFA=90°﹣∠CAF,
同理在Rt△AED中,∠AED=90°﹣∠DAE.
又∵AF平分∠CAB,
∴∠CAF=∠DAE,
∴∠AED=∠CFE,
又∵∠CEF=∠AED,
∴∠CEF=∠CFE.
26.解:∵∠ACB=90°,∠A=30°,AB=8,
∴BC=AB=×8=4,
∵CD⊥AB,
∴∠BCD+∠ABC=90°,
又∵∠A+∠ABC=90°,
∴∠BCD=∠A=30°,
∴BD=BC=×4=2,
在Rt△BCD中,CD===2,
∵∠E=45°,
∴∠DCE=90°﹣45°=45°,
∴∠DCE=∠E,
∴DE=CD=2,
∴BE=DE﹣BD=2﹣2.
27.(1)证明:∵BE⊥AC,CF⊥AB,M为BC的中点,
∴ME=BC,MF=BC,
∴ME=MF;
(2)解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵MF=MB,ME=MC,
∴∠MFB=∠ABC,∠MEC=∠ACB,
∴∠BMF+∠CME=360°﹣130°×2=100°,
∴∠FME=180°﹣100°=80°.
解直角三角形》单元测试卷
一.选择题
1.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
A.AC2=AD?AB
B.CD2=CA?CB
C.CD2=AD?DB
D.BC2=BD?BA
2.如图,在Rt△ABC,∠BAC=90°,AD⊥BC,AB=10,BD=6,则BC的值为( )
A.
B.
C.
D.
3.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A﹣∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
4.如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
A.图中有三个直角三角形
B.∠1=∠2
C.∠1和∠B都是∠A的余角
D.∠2=∠A
5.在△ABC中,已知∠C=90°,AB=13,BC=5,则cosA的值是( )
A.
B.
C.
D.
6.如图,在Rt△ABC中,∠C=90°,如果AC=5,AB=13,那么cosA的值为( )
A.
B.
C.
D.
7.如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
A.2cm
B.4cm
C.2cm
D.4cm
8.如图,CD是直角△ABC斜边AB上的高,CB>CA,图中相等的角共有( )
A.2对
B.3对
C.4对
D.5对
9.已知在Rt△ABC中,∠C=90°,AC=,AB=4,则cosB的值是( )
A.
B.
C.
D.
10.如图,AB⊥AF,EF⊥AF,BE与AF交于点C,点D是BC的中点,∠AEB=2∠B.若BC=8,EF=,则AF的长是( )
A.
B.
C.3
D.5
二.填空题
11.在直角三角形中,一个锐角为38°,则另一个锐角等于
°.
12.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为
.
13.如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=
.
14.如图,BC⊥ED于O,∠A=27°,∠D=20°,则∠B=
,∠ACB=
.
15.如图,Rt△ABC中,∠C=90°,∠A=30°,AB=8cm,则BC=
cm.
16.在直角三角形中,若两条直角边长分别为6cm和8cm,则斜边上的中线为
cm.
17.如图,△ABC的三个顶点都在正方形网格的格点上,则tan∠A=
18.在△ABC中,∠C=90°,tanA=,则cosB=
.
19.在△ABC中,∠C=90°,AC=4,BC=3,则tanB=
.
20.在△ABC中,∠A=90°,∠B、∠C的角平分线BE、CF交于点O,那么∠BOC的度数是
.
三.解答题
21.如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠EDF.
22.如图,AD是Rt△ABC斜边上的高,若AB=4cm,BC=10cm,求BD的长.
23.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.求BD的长.
24.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)求证:CD∥EF;
(2)若∠A=70°,求∠FEC的度数.
25.如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
26.已知:如图,△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,点E在AB的延长线上,∠E=45°,若AB=8,求BE的长.
27.如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.
(1)求证:ME=MF;
(2)若∠A=50°,求∠FME的度数.
参考答案与试题解析
一.选择题
1.解:∵∠ACB=90°,CD⊥AB于点D,
∴AC2=AD?AB,CD2=DA?DB,BC2=BD?BA.
故选:B.
2.解:根据射影定理得:AB2=BD×BC,
∴BC==.
故选:D.
3.解:A选项,∠A+∠B=∠C,即2∠C=180°,∠C=90°,为直角三角形,不符合题意;
B选项,∠A﹣∠B=∠C,即2∠A=180°,∠A=90°,为直角三角形,不符合题意;
C选项,∠A:∠B:∠C=1:2:3,即∠A+∠B=∠C,同A选项,不符合题意;
D选项,∠A=∠B=3∠C,即7∠C=180°,三个角没有90°角,故不是直角三角形,符合题意.
故选:D.
4.解:∵∠ACB=90°,CD⊥AB,垂足为D,
∴△ACD∽△CBD∽△ABC.
A、∵图中有三个直角三角形Rt△ACD、Rt△CBD、Rt△ABC;故本选项正确;
B、应为∠1=∠B、∠2=∠A;故本选项错误;
C、∵∠1=∠B、∠2=∠A,而∠B是∠A的余角,∴∠1和∠B都是∠A的余角;故本选项正确;
D、∵∠2=∠A;故本选项正确.
故选:B.
5.解:∵∠C=90°,AB=13,BC=5,
∴AC==12,
∴cosA==,
故选:D.
6.解:∵∠C=90°,AC=5,AB=13,
∴cosA==,
故选:A.
7.解:过点C作CD⊥AD,∴CD=2,
在直角三角形ADC中,
∵∠CAD=30°,
∴AC=2CD=2×2=4,
又∵三角板是有45°角的三角板,
∴AB=AC=4,
∴BC2=AB2+AC2=42+42=32,
∴BC=4,
故选:D.
8.解:∵CD是直角△ABC斜边AB上的高,
∴∠ACB=∠ADC=∠CDB=90°,
∴∠A+∠ACD=∠ACD+∠DCB=90°,
∴∠A=∠DCB,
同理得:∠B=∠ACD,
∴相等的角一共有5对,
故选:D.
9.解:如图:
∵∠C=90°,AC=,AB=4,
∴BC===1,
∴cosB==,
故选:C.
10.解:∵AB⊥AF,
∴∠FAB=90°,
∵点D是BC的中点,
∴AD=BD=BC,
∴∠DAB=∠B,
∴∠ADE=∠B+∠BAD=2∠B,
∵∠AEB=2∠B,
∴∠AED=∠ADE,
∴AE=AD,
∵BC=8,
∴AE=AD=4,
∵EF=,EF⊥AF,
∴AF===3,
故选:C.
二.填空题
11.解:在直角三角形中,一个锐角为38°,则另一个锐角等于90°﹣38°=52°.
故答案为52.
12.解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,
∴CD2=AD?BD=8×2,
则CD=4.
故答案是:4.
13.解:在Rt△ABC中,AB==5,
由射影定理得,AC2=AD?AB,
∴AD==,
故答案为:.
14.解:∵∠A=27°,∠D=20°,
∴∠BEO=∠A+∠D=27°+20°=47°,
∵BC⊥ED,
∴∠B=90°﹣∠BEO=90°﹣47°=43°;
在Rt△COD中,∠ACB=∠D+∠COD=20°+90°=110°.
故答案为:43°;110°.
15.解:根据含30度角的直角三角形的性质可知:BC=AB=4cm.
故答案为:4.
16.解:根据勾股定理得,斜边==10cm,
∴斜边上的中线=×斜边=×10=5cm.
故答案为:5.
17.解:作BE⊥AC于E,则BE=6,AE=5,
∴tan∠A===1.2
故答案为1.2.
18.解:法一:
利用三角函数的定义及勾股定理求解.
∵在Rt△ABC中,∠C=90°,tanA=,
设a=x,b=3x,则c=2x,
∴cosB==.
法二:
利用特殊角的三角函数值求解.
∵tanA=
∴∠A=30°,
∵∠C=90°
∴∠B=60°,
∴cosB=cos60°=.
故答案为:.
19.解:△ABC中,∠C=90°,AC=4,BC=3,
∴AB==5.
∴tanB==.
20.解:∵∠A=90°,
∴∠ABC+∠ACB=90°,
∵角平分线BE、CF交于点O,
∴∠OBC+∠OCB=45°,
∴∠BOC=180°﹣45°=135°.
故答案为135°.
三.解答题
21.解:∵∠AFD=152°,
∴∠DFC=28°,
∴∠B=∠C,FD⊥BC,DE⊥AB,
∴∠EDB=∠DFC=28°,
∴∠EDF=180°﹣∠EDB﹣∠FDC=180°﹣90°﹣28°=62°.
22.解:由射影定理得,AB2=BD?BC,
则BD==1.6.
23.解:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠CDB=∠ACB=90°,
∴∠ACD+∠BCD=90°,∠BCD+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴=,
∵AD=2,CD=4,
∴=,
∴BD=8.
24.(1)证明:∵CD⊥AB,EF⊥AB,
∴CD∥EF;
(2)解:∵CD⊥AB,
∴∠ACD=90°﹣70°=20°,
∵∠ACB=90°,CE平分∠ACB,
∴∠ACE=45°,
∴∠DCE=45°﹣20°=25°,
∵CD∥EF,
∴∠FEC=∠DCE=25°.
25.证明:(1)∵∠ACB=90゜,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B;
(2)在Rt△AFC中,∠CFA=90°﹣∠CAF,
同理在Rt△AED中,∠AED=90°﹣∠DAE.
又∵AF平分∠CAB,
∴∠CAF=∠DAE,
∴∠AED=∠CFE,
又∵∠CEF=∠AED,
∴∠CEF=∠CFE.
26.解:∵∠ACB=90°,∠A=30°,AB=8,
∴BC=AB=×8=4,
∵CD⊥AB,
∴∠BCD+∠ABC=90°,
又∵∠A+∠ABC=90°,
∴∠BCD=∠A=30°,
∴BD=BC=×4=2,
在Rt△BCD中,CD===2,
∵∠E=45°,
∴∠DCE=90°﹣45°=45°,
∴∠DCE=∠E,
∴DE=CD=2,
∴BE=DE﹣BD=2﹣2.
27.(1)证明:∵BE⊥AC,CF⊥AB,M为BC的中点,
∴ME=BC,MF=BC,
∴ME=MF;
(2)解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵MF=MB,ME=MC,
∴∠MFB=∠ABC,∠MEC=∠ACB,
∴∠BMF+∠CME=360°﹣130°×2=100°,
∴∠FME=180°﹣100°=80°.
