人教版数学八年级上册13.3.1 等腰三角形同步练习(Word版含答案)
文档属性
| 名称 | 人教版数学八年级上册13.3.1 等腰三角形同步练习(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 515.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 07:13:39 | ||
图片预览
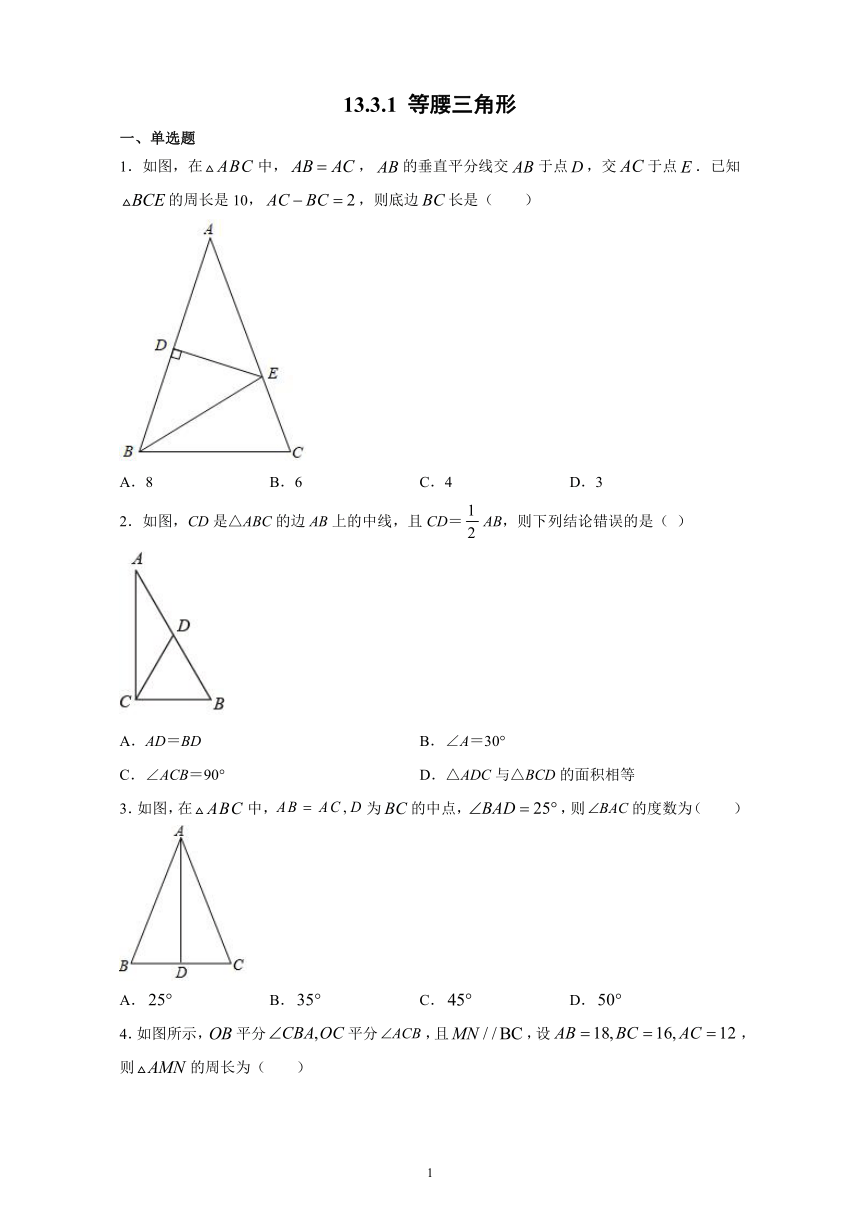


文档简介
13.3.1
等腰三角形
一、单选题
1.如图,在中,,的垂直平分线交于点,交于点.已知的周长是10,,则底边长是(
)
A.8
B.6
C.4
D.3
2.如图,CD是△ABC的边AB上的中线,且CD=AB,则下列结论错误的是(
)
A.AD=BD
B.∠A=30°
C.∠ACB=90°
D.△ADC与△BCD的面积相等
3.如图,在中,为的中点,,则的度数为(
)
A.
B.
C.
D.
4.如图所示,平分平分,且,设,则的周长为(
)
A.30
B.33
C.36
D.39
5.有下列说法:①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高线相等:④等腰三角形两底角的平分线相等其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
6.如图,正方形网格中,网格线的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得为等腰三角形,则点C的个数是(
)
A.6
B.8
C.9
D.10
7.如图,在中,,垂足为,垂直平分,交于点,交于点,,若的周长为cm,cm,则(
)
A.cm
B.cm
C.cm
D.cm
8.若一个等腰三角形的两边分别是和,那么这个等腰三角形的(
)
A.腰长为
B.腰长为
C.周长为
D.周长为或
9.如图,等腰中,,以为圆心,长为半径画弧,分别交、于、两点,并连接、,若,则(
)
A.
B.
C.
D.
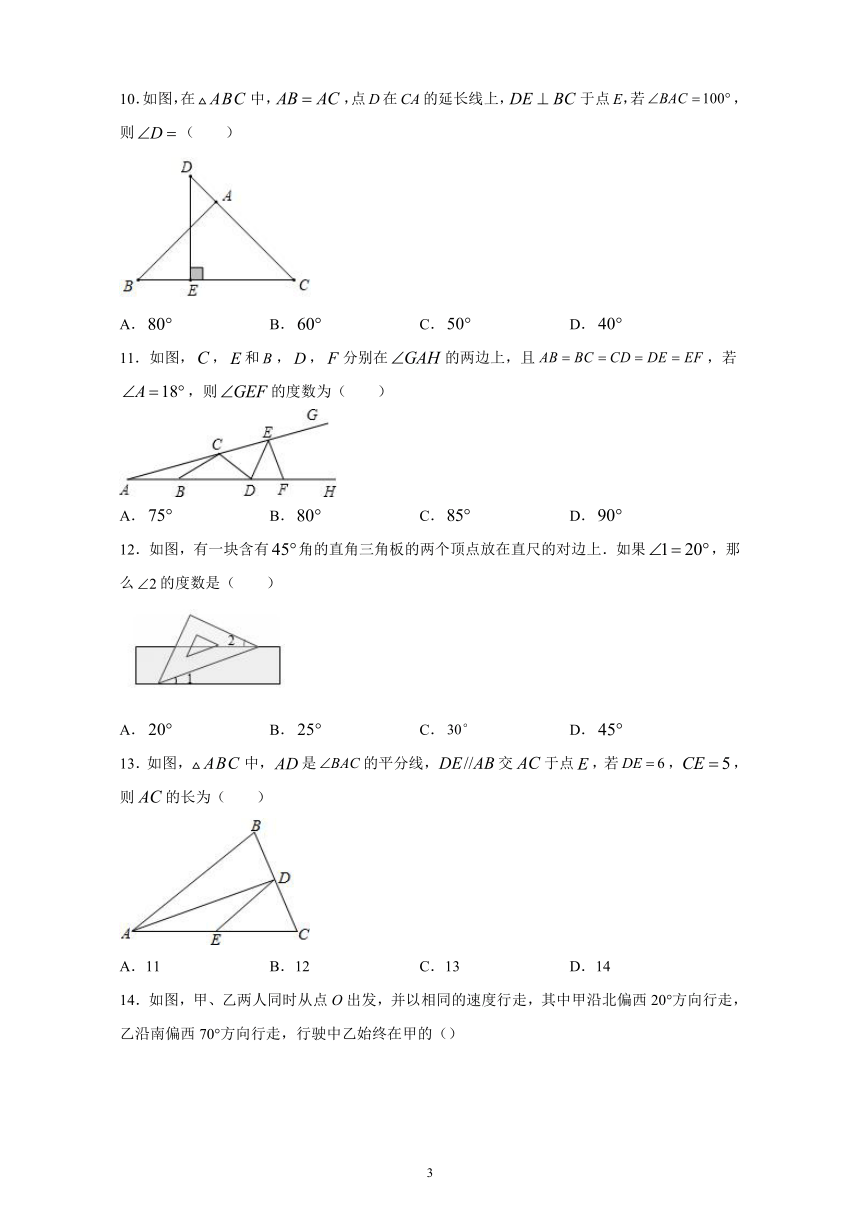
10.如图,在中,,点D在CA的延长线上,于点E,若,则(
)
A.
B.
C.
D.
11.如图,,和,,分别在的两边上,且,若,则的度数为(
)
A.
B.
C.
D.
12.如图,有一块含有角的直角三角板的两个顶点放在直尺的对边上.如果,那么的度数是(
)
A.
B.
C.
D.
13.如图,中,是的平分线,交于点,若,,则的长为(
)
A.11
B.12
C.13
D.14
14.如图,甲、乙两人同时从点O出发,并以相同的速度行走,其中甲沿北偏西20°方向行走,乙沿南偏西70°方向行走,行驶中乙始终在甲的()
A.南偏西30°方向上
B.南偏西35°方向上
C.南偏西25°方向上
D.南偏西20°方向上
15.如图在△ABC中,AB=AC,AD=BC=8,点E,F是中线AD上的两点,则图中阴影部分的面积是(
)
A.6
B.9
C.16
D.24
二、填空题
16.若一条长为32cm的细线能围成一边长等于8cm的等腰三角形,则该等腰三角形的腰长为___cm.
17.已知等腰的一个角是,则这个三角形的其余两个角为________.
18.如图,已知,,点为的外心,若,则____.
19.如图所示,在中,,则_____.
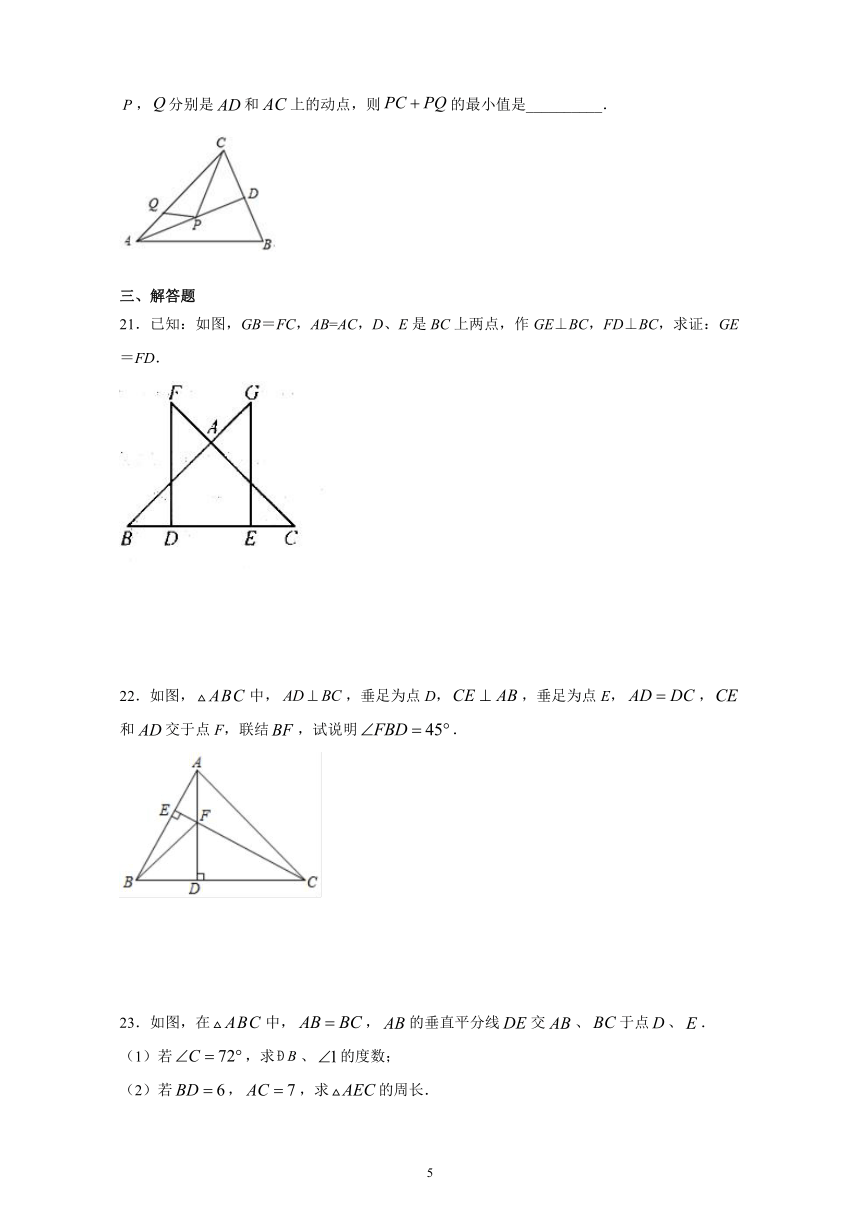
20.如图,在中,,,,是的平分线.若,分别是和上的动点,则的最小值是__________.
三、解答题
21.已知:如图,GB=FC,AB=AC,D、E是BC上两点,作GE⊥BC,FD⊥BC,求证:GE=FD.
22.如图,中,,垂足为点D,,垂足为点E,,和交于点F,联结,试说明.
23.如图,在中,,的垂直平分线交、于点、.
(1)若,求、的度数;
(2)若,,求的周长.
24.如图,在中,,点,在上,.
(1)求证:≌.
(2)若,,求的长.
25.如图,在中,,D为中点,点N在线段上,交于点M,.
(1)求度数;
(2)求的周长.
参考答案
1.C
解:∵△BCE的周长为10,
∴BE+EC+BC=10.
∵AB的垂直平分线交AB于点D,
∴AE=BE,
∴AE+EC+BC=10,
即AC+BC=10,
∵AC-BC=2,
∴BC=4,
故选:C.
2.B
解:A、∵CD是△ABC的边AB上的中线,
∴AD=BD,故A正确,不符合题意;
B、不能判定出∠A=30°,故B错误,符合题意;
C、∵CD=CD=AB,
∴CD=AD=BD,
∴CD=AB,
∴∠A=∠ACD,∠B=∠BCD,
∵∠A+∠ACD+∠B+∠BCD=180°,
∴∠ACD+∠BCD=90°,
∴∠ACD=90°,故C正确,不符合题意;
D、∵△ADC与△BCD边AD和BD上的高相等,且AD=BD,
∴△ADC与△BCD的面积相等,故D正确,不符合题意;
故选:B.
3.D
解:∵AB=AC,点D为BC的中点,
∴∠BAD=∠CAD=25°,
∴∠BAC=50°,
故选:D.
4.A
解:∵BO平分∠CBA,CO平分∠ACB,
∴∠MBO=∠OBC,∠OCN=∠OCB,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MBO=∠MOB,∠NOC=∠NCO,
∴MO=MB,NO=NC,
∵AB=18,AC=12,
∴△AMN的周长=AM+MN+AN=AB+AC=18+12=30.
故选:A.
5.D
解:①等腰三角形的两腰相等;正确;
②等腰三角形的两底角相等;正确;
③等腰三角形底边上的中线与底边上的高相等;正确;
④等腰三角形两底角的平分线相等.正确.
故选:D.
6.D
解:如图,分情况讨论:
①AB为等腰△ABC的底边时,符合条件的C点有6个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:D.
7.A
解:∵AD⊥BC,BD=DE,EF垂直平分AC
∴AB=AE=EC
∵△ABC周长是26cm,AF=5cm
∴AC=10cm
∴AB+BC=16cm
∴AB+BE+EC=16cm
即2DE+2EC=16cm
∴DE+EC=8cm
∴DC=DE+EC=8cm
故选A.
8.B
解:当3为底时,其它两边都为6cm,3cm、6cm、6cm可以构成三角形,周长为15cm;
当3cm为腰时,其它两边为3cm和6cm,因为3+3=6(cm),所以不能构成三角形,故舍去,
所以3cm不能作为腰长,6cm可以作为腰长,周长只能是15cm.
故选:B.
9.A
解:
由题意:
故选A
10.C
解:∵,
∴.
∵,
∴.
∵,
∴,
∴.
故选:C.
11.D
解:∵AB=BC,
∴∠ACB=∠A=18°,
∴∠CBD=∠A+∠ACB=36°,
∵BC=CD,
∴∠CDB=∠CBD=36°,
∴∠DCE=∠A+∠CDA=18°+36°=54°,
∵CD=DE,
∴∠CED=∠DCE=54°,
∴∠EDF=∠A+∠AED=18°+54°=72°,
∵DE=EF,
∴∠EFD=∠EDF=72°,
∴∠GEF=∠A+∠AFE=18°+72°=90°.
故选:D.
12.B
解:由题知,如图,为等腰直角三角形,∴
;
直尺边相互平行,∴
,∴;
又,∴
;
故选:B;
13.A
解:中,是的平分线,
,
,
∴∠BAD=∠ADE,
,
∵,,
,
.
故选:.
14.C
解:由题意得,∠1=20°,∠2=70°,AO=BO,
∴∠AOB=90°,
∴∠ABO=∠BAO=45°,
∵∠3=∠1=20°,
∴∠4=25°,
∴乙始终在甲的南偏西25°方向上.
故选:C.
15.C
解:∵AB=AC,AD=BC=8,AD是△ABC的中线,
∴BD=DC=BC=4,AD⊥BC,
∴△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:×BC×AD=×8×8=32,
∴图中阴影部分的面积是S△ABC=16.
故选:C.
16.12
解:若腰长为8cm,则此三角形的另一边长为32-8-8=16(cm),
而8+8=16,无法构成三角形,
∴此情形舍去;
若底边为8cm,则腰长为(32-8)÷2=12(cm),
此时12+12>8,12+8>8,可以构成三角形.
故答案为:12.
17.70°,70°或40°,100°
解:①40°角是顶角时,底角=(180°-40°)=×140°=70°,
另两个角为70°,70°;
②40°角是底角时,顶角为180°-40°×2=100°,
另两个角为40°,100°,
所以,另两个角度数为70°,70°或40°,100°.
故答案为:70°,70°或40°,100°.
18.140
解:∵,
∴∠AED==70°
如图,延长BF,交AE于H点
∵点为的外心
∴F点在AE的垂直平分线上
又
∴BH是AE的垂直平分线,
∴BH⊥AE,
∴∠FBE=90°-∠AED=20°,
同理可得∠FCD=90°-70=20°
∴180°-∠FBE-∠FCD=140°
故答案为:140.
19.30°
解:∵∠ABC=120°,
∴∠A+∠C=180°-120°=60°.
∵AM=AN,CN=CP,
∴∠ANM=,∠CNP=,
∴∠MNP=180°--
=180°-90°+∠A-90°+∠C
=(∠A+∠C)
=×60°
=30°,
故答案为:30°.
20.9.6
解:∵,是的平分线,
∴(等腰三角形三线合一),
设点Q关于直线AD对称的对称点为,连接,如图,
∵是的平分线,
∴点在AB上(根据轴对称性质和角平分线性质),
∴,
∴当且C、P、三点共线时,
有最小值,即,
∵,
,,,
∴,
解得,,
∴的最小值是9.6,
故答案为:9.6
21.见详解
证明:∵AB=AC,
∴∠B=∠C.
∵GE⊥BC,FD⊥BC,
∴∠GEB=∠FDC=90°,
又∵GB=FC,
∴△BEG≌△CDF(AAS),
∴GE=FD.
22.见解析.
解:∵,(已知),
∴,,(垂直的意义),
∴(等量代换).
∵,
∴(等量代换).
∵(对顶角相等),
∴
在与中,
∴(ASA),
∴(全等三角形的对应边相等),
∴.
∵,
∴.
23.(1);;(2)19
解:∵AB的垂直平分线分别交AB,BC于点D,E,
∴BE=AE,∠ADE=∠BDE,
∵AB=BC,
∴∠C=∠BAC=∠3+∠4=72°,
∴∠B=180°-∠C-∠BAC=180°-72°-72°=36°,
∴∠3=∠B=36°,
∴∠1=90°-∠3=54°;
(2)∵BD=6,
∴AB=2BD=2×6=12,
∴BC=12,
∵AE=BE,
∴AE+CE+AC=BC+AC=12+7=19.
即△AEC的周长为19.
24.(1)见解析;(2)2
解:(1)∵,
∴,
∵,
∴≌.
(2)∵,,
∴,
∴,
∵≌,
∴.
25.(1)20°;(2)11
解:(1)∵
∴是等腰三角形.
∵,
∴.
又∵D为中点,
∴平分,即.
∴.
(2)∵,
∴.
又∵
∴.
∴是等腰三角形.
∴.
∵,,
∴的周长为:
.
等腰三角形
一、单选题
1.如图,在中,,的垂直平分线交于点,交于点.已知的周长是10,,则底边长是(
)
A.8
B.6
C.4
D.3
2.如图,CD是△ABC的边AB上的中线,且CD=AB,则下列结论错误的是(
)
A.AD=BD
B.∠A=30°
C.∠ACB=90°
D.△ADC与△BCD的面积相等
3.如图,在中,为的中点,,则的度数为(
)
A.
B.
C.
D.
4.如图所示,平分平分,且,设,则的周长为(
)
A.30
B.33
C.36
D.39
5.有下列说法:①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高线相等:④等腰三角形两底角的平分线相等其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
6.如图,正方形网格中,网格线的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得为等腰三角形,则点C的个数是(
)
A.6
B.8
C.9
D.10
7.如图,在中,,垂足为,垂直平分,交于点,交于点,,若的周长为cm,cm,则(
)
A.cm
B.cm
C.cm
D.cm
8.若一个等腰三角形的两边分别是和,那么这个等腰三角形的(
)
A.腰长为
B.腰长为
C.周长为
D.周长为或
9.如图,等腰中,,以为圆心,长为半径画弧,分别交、于、两点,并连接、,若,则(
)
A.
B.
C.
D.
10.如图,在中,,点D在CA的延长线上,于点E,若,则(
)
A.
B.
C.
D.
11.如图,,和,,分别在的两边上,且,若,则的度数为(
)
A.
B.
C.
D.
12.如图,有一块含有角的直角三角板的两个顶点放在直尺的对边上.如果,那么的度数是(
)
A.
B.
C.
D.
13.如图,中,是的平分线,交于点,若,,则的长为(
)
A.11
B.12
C.13
D.14
14.如图,甲、乙两人同时从点O出发,并以相同的速度行走,其中甲沿北偏西20°方向行走,乙沿南偏西70°方向行走,行驶中乙始终在甲的()
A.南偏西30°方向上
B.南偏西35°方向上
C.南偏西25°方向上
D.南偏西20°方向上
15.如图在△ABC中,AB=AC,AD=BC=8,点E,F是中线AD上的两点,则图中阴影部分的面积是(
)
A.6
B.9
C.16
D.24
二、填空题
16.若一条长为32cm的细线能围成一边长等于8cm的等腰三角形,则该等腰三角形的腰长为___cm.
17.已知等腰的一个角是,则这个三角形的其余两个角为________.
18.如图,已知,,点为的外心,若,则____.
19.如图所示,在中,,则_____.
20.如图,在中,,,,是的平分线.若,分别是和上的动点,则的最小值是__________.
三、解答题
21.已知:如图,GB=FC,AB=AC,D、E是BC上两点,作GE⊥BC,FD⊥BC,求证:GE=FD.
22.如图,中,,垂足为点D,,垂足为点E,,和交于点F,联结,试说明.
23.如图,在中,,的垂直平分线交、于点、.
(1)若,求、的度数;
(2)若,,求的周长.
24.如图,在中,,点,在上,.
(1)求证:≌.
(2)若,,求的长.
25.如图,在中,,D为中点,点N在线段上,交于点M,.
(1)求度数;
(2)求的周长.
参考答案
1.C
解:∵△BCE的周长为10,
∴BE+EC+BC=10.
∵AB的垂直平分线交AB于点D,
∴AE=BE,
∴AE+EC+BC=10,
即AC+BC=10,
∵AC-BC=2,
∴BC=4,
故选:C.
2.B
解:A、∵CD是△ABC的边AB上的中线,
∴AD=BD,故A正确,不符合题意;
B、不能判定出∠A=30°,故B错误,符合题意;
C、∵CD=CD=AB,
∴CD=AD=BD,
∴CD=AB,
∴∠A=∠ACD,∠B=∠BCD,
∵∠A+∠ACD+∠B+∠BCD=180°,
∴∠ACD+∠BCD=90°,
∴∠ACD=90°,故C正确,不符合题意;
D、∵△ADC与△BCD边AD和BD上的高相等,且AD=BD,
∴△ADC与△BCD的面积相等,故D正确,不符合题意;
故选:B.
3.D
解:∵AB=AC,点D为BC的中点,
∴∠BAD=∠CAD=25°,
∴∠BAC=50°,
故选:D.
4.A
解:∵BO平分∠CBA,CO平分∠ACB,
∴∠MBO=∠OBC,∠OCN=∠OCB,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MBO=∠MOB,∠NOC=∠NCO,
∴MO=MB,NO=NC,
∵AB=18,AC=12,
∴△AMN的周长=AM+MN+AN=AB+AC=18+12=30.
故选:A.
5.D
解:①等腰三角形的两腰相等;正确;
②等腰三角形的两底角相等;正确;
③等腰三角形底边上的中线与底边上的高相等;正确;
④等腰三角形两底角的平分线相等.正确.
故选:D.
6.D
解:如图,分情况讨论:
①AB为等腰△ABC的底边时,符合条件的C点有6个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:D.
7.A
解:∵AD⊥BC,BD=DE,EF垂直平分AC
∴AB=AE=EC
∵△ABC周长是26cm,AF=5cm
∴AC=10cm
∴AB+BC=16cm
∴AB+BE+EC=16cm
即2DE+2EC=16cm
∴DE+EC=8cm
∴DC=DE+EC=8cm
故选A.
8.B
解:当3为底时,其它两边都为6cm,3cm、6cm、6cm可以构成三角形,周长为15cm;
当3cm为腰时,其它两边为3cm和6cm,因为3+3=6(cm),所以不能构成三角形,故舍去,
所以3cm不能作为腰长,6cm可以作为腰长,周长只能是15cm.
故选:B.
9.A
解:
由题意:
故选A
10.C
解:∵,
∴.
∵,
∴.
∵,
∴,
∴.
故选:C.
11.D
解:∵AB=BC,
∴∠ACB=∠A=18°,
∴∠CBD=∠A+∠ACB=36°,
∵BC=CD,
∴∠CDB=∠CBD=36°,
∴∠DCE=∠A+∠CDA=18°+36°=54°,
∵CD=DE,
∴∠CED=∠DCE=54°,
∴∠EDF=∠A+∠AED=18°+54°=72°,
∵DE=EF,
∴∠EFD=∠EDF=72°,
∴∠GEF=∠A+∠AFE=18°+72°=90°.
故选:D.
12.B
解:由题知,如图,为等腰直角三角形,∴
;
直尺边相互平行,∴
,∴;
又,∴
;
故选:B;
13.A
解:中,是的平分线,
,
,
∴∠BAD=∠ADE,
,
∵,,
,
.
故选:.
14.C
解:由题意得,∠1=20°,∠2=70°,AO=BO,
∴∠AOB=90°,
∴∠ABO=∠BAO=45°,
∵∠3=∠1=20°,
∴∠4=25°,
∴乙始终在甲的南偏西25°方向上.
故选:C.
15.C
解:∵AB=AC,AD=BC=8,AD是△ABC的中线,
∴BD=DC=BC=4,AD⊥BC,
∴△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:×BC×AD=×8×8=32,
∴图中阴影部分的面积是S△ABC=16.
故选:C.
16.12
解:若腰长为8cm,则此三角形的另一边长为32-8-8=16(cm),
而8+8=16,无法构成三角形,
∴此情形舍去;
若底边为8cm,则腰长为(32-8)÷2=12(cm),
此时12+12>8,12+8>8,可以构成三角形.
故答案为:12.
17.70°,70°或40°,100°
解:①40°角是顶角时,底角=(180°-40°)=×140°=70°,
另两个角为70°,70°;
②40°角是底角时,顶角为180°-40°×2=100°,
另两个角为40°,100°,
所以,另两个角度数为70°,70°或40°,100°.
故答案为:70°,70°或40°,100°.
18.140
解:∵,
∴∠AED==70°
如图,延长BF,交AE于H点
∵点为的外心
∴F点在AE的垂直平分线上
又
∴BH是AE的垂直平分线,
∴BH⊥AE,
∴∠FBE=90°-∠AED=20°,
同理可得∠FCD=90°-70=20°
∴180°-∠FBE-∠FCD=140°
故答案为:140.
19.30°
解:∵∠ABC=120°,
∴∠A+∠C=180°-120°=60°.
∵AM=AN,CN=CP,
∴∠ANM=,∠CNP=,
∴∠MNP=180°--
=180°-90°+∠A-90°+∠C
=(∠A+∠C)
=×60°
=30°,
故答案为:30°.
20.9.6
解:∵,是的平分线,
∴(等腰三角形三线合一),
设点Q关于直线AD对称的对称点为,连接,如图,
∵是的平分线,
∴点在AB上(根据轴对称性质和角平分线性质),
∴,
∴当且C、P、三点共线时,
有最小值,即,
∵,
,,,
∴,
解得,,
∴的最小值是9.6,
故答案为:9.6
21.见详解
证明:∵AB=AC,
∴∠B=∠C.
∵GE⊥BC,FD⊥BC,
∴∠GEB=∠FDC=90°,
又∵GB=FC,
∴△BEG≌△CDF(AAS),
∴GE=FD.
22.见解析.
解:∵,(已知),
∴,,(垂直的意义),
∴(等量代换).
∵,
∴(等量代换).
∵(对顶角相等),
∴
在与中,
∴(ASA),
∴(全等三角形的对应边相等),
∴.
∵,
∴.
23.(1);;(2)19
解:∵AB的垂直平分线分别交AB,BC于点D,E,
∴BE=AE,∠ADE=∠BDE,
∵AB=BC,
∴∠C=∠BAC=∠3+∠4=72°,
∴∠B=180°-∠C-∠BAC=180°-72°-72°=36°,
∴∠3=∠B=36°,
∴∠1=90°-∠3=54°;
(2)∵BD=6,
∴AB=2BD=2×6=12,
∴BC=12,
∵AE=BE,
∴AE+CE+AC=BC+AC=12+7=19.
即△AEC的周长为19.
24.(1)见解析;(2)2
解:(1)∵,
∴,
∵,
∴≌.
(2)∵,,
∴,
∴,
∵≌,
∴.
25.(1)20°;(2)11
解:(1)∵
∴是等腰三角形.
∵,
∴.
又∵D为中点,
∴平分,即.
∴.
(2)∵,
∴.
又∵
∴.
∴是等腰三角形.
∴.
∵,,
∴的周长为:
.
