人教版数学八年级上册13.1.1 轴对称同步练习(word解析版)
文档属性
| 名称 | 人教版数学八年级上册13.1.1 轴对称同步练习(word解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 530.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 09:26:58 | ||
图片预览

文档简介
13.1.1
轴对称
一、单选题
1.下列图形中,是轴对称图形的是( )
A.
B.
C.
D.
2.点关于轴的对称点的坐标为(
).
A.
B.
C.
D.
3.如图,在长方形纸片中,,将长方形纸片沿折叠,点落在点处,交边于点,若,则等于(
)
A.
B.
C.
D.
4.如图,为一长条形纸带,,将沿折叠,、两点分别与、对应,若,则的度数为(
)
A.60°
B.65°
C.72°
D.75°
5.下列图形中,是轴对称图形的是( )
A.平行四边形
B.直角梯形
C.正五边形
D.直角三角形
6.如图,为等腰直角三角形,、将按如图方式进行折叠,使点A与边上的点F重合,折痕分别与、交于点D、点E.下列结论:①;②;③;④.其中一定正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
7.如图,中,D、E、F三点分别在AB、BC、AC上,且四边形BEFD是以DE为对称轴的线对称图形,四边形CFDE是以FE为对称轴的线对称图形若,则的度数为何?(
)
A.65
B.70
C.75
D.80
8.如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是(
)
A.0
B.5
C.6
D.7
9.如图,在中,,沿图中虚线翻折,使得点B落在上的点D处,则等于(
)
A.160°
B.150°
C.140°
D.110°
10.如图,在中,,将沿直线翻折,点落在点的位置,则的度数是(
)
A.
B.
C.
D.
11.是网格中的格点三角形(三角形的各顶点都在网格的交叉点上),如图建立直角坐标系,将该三角形先向下平移2个单位,然后再将平移后的图形沿y轴翻折,得到,则点B对应点的坐标为(
)
A.
B.
C.
D.
12.如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为D,△ABD与△ADB’关于直线AD对称,点B的对称点是点B’,若∠B’AC=14°,则∠B的度数为
(
)
A.38°
B.48°
C.50°
D.52°
13.在下列画的四个三角形中,与成轴对称的是( )
A.
B.
C.
D.
14.如图,已知与关于直线l对称,,则的度数为(
)
A.
B.
C.
D.
15.如图是一个经过改造的规则为的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是(
)
A.1号袋
B.2号袋
C.3号袋
D.4号袋
二、填空题
16.如图,在四边形中,,,在、上分别取一点、,使的周长最小,则___°.
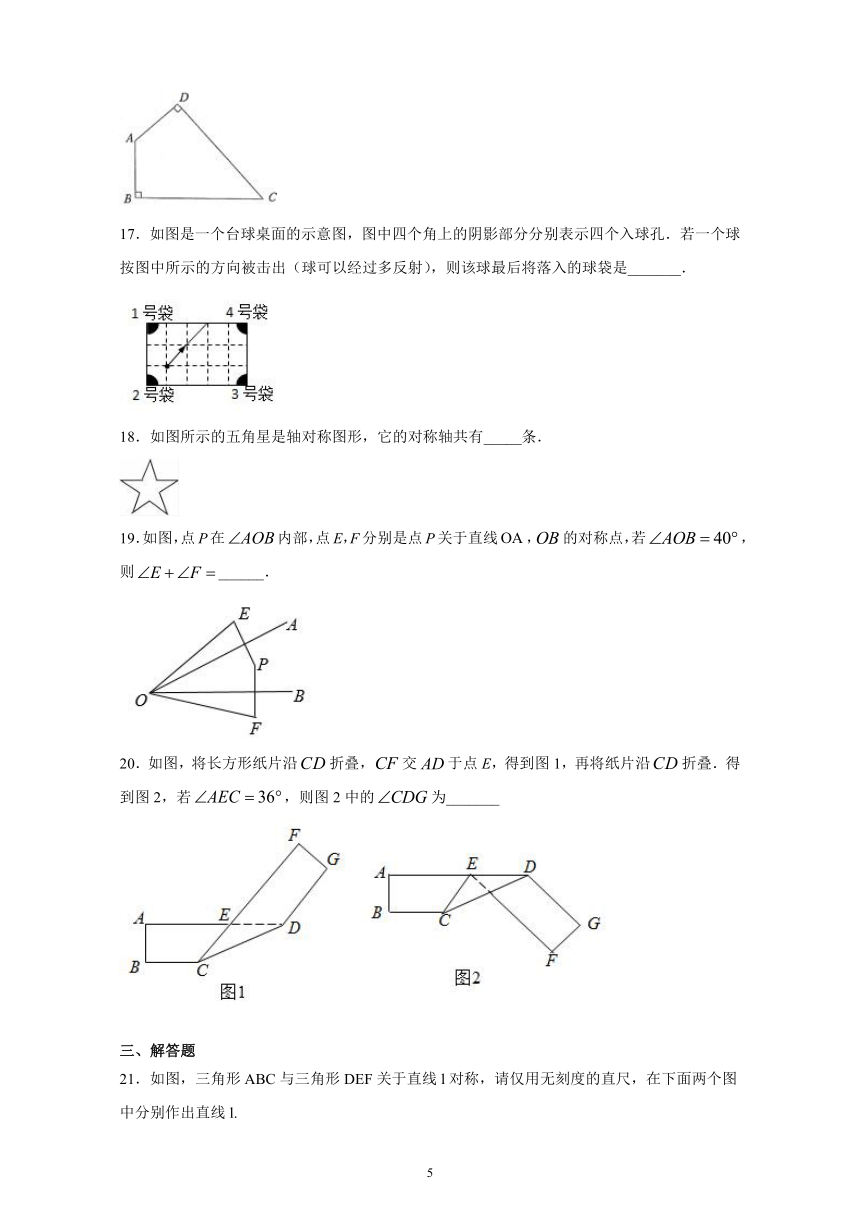
17.如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多反射),则该球最后将落入的球袋是_______.
18.如图所示的五角星是轴对称图形,它的对称轴共有_____条.
19.如图,点P在内部,点E,F分别是点P关于直线,的对称点,若,则______.
20.如图,将长方形纸片沿折叠,交于点E,得到图1,再将纸片沿折叠.得到图2,若,则图2中的为_______
三、解答题
21.如图,三角形ABC与三角形DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
22.手工制作课上,老师先将一张长方形纸片折叠成如图所示的那样,若折痕与一条边BC的夹角∠EFB=30°,你能说出∠EGF的度数吗?
23.已知:如图,是一个长方形的台球面,有、两球分别位于图中所在位置,试问怎样撞击球,才能使先碰到台边反弹后再击中球?在图中画出球的运动线路.
24.如图,已知在一张纸条上画有一条数轴.
(1)沿过原点且垂直于数轴的直线折叠纸条,则表示-3的点与表示___________的点重合;
(2)为数轴上一点,沿过点且垂直于数轴的直线折叠纸条,当表示-3的点与表示1的点重合时,
①点所表示的数为__________;
②若数轴上的,两点也同时重合,且,求点所表示的数.
25.如图,在平面直角坐标系中,A
(-1,
4),
B(3,
2),
C(-1,0)
(1)
点A关于y轴的对称点的坐标为
,点B关于x轴的对称点的坐标为
,
线段AC的垂直平分线与y轴的交点D的坐标为
.
(2)求(1)中的△的面积.
参考答案
1.B
解:A.不是轴对称图形,不符合题意;
B.是轴对称图形,符合题意;
C.不是轴对称图形,不符合题意;
D.不是轴对称图形,不符合题意.
故选:B.
2.A
解:点坐标关于轴对称的变换规律:横坐标变为相反数,纵坐标不变,
则点关于轴的对称点的坐标为,
故选:A.
3.D
解:由折叠的性质得∠ADB=∠EDB,
∴∠ADF=2∠ADB,
∵∠ADB=20°,
∴∠ADF=2×20°=40°,
∵AD∥BC,
∴∠DFC=∠ADF=40°,
故选:D.
4.A
解:由翻折的性质可知:∠AEF=∠FEA′,
∵AB∥CD,
∴∠AEF=∠1,
∵∠1=∠2,设∠2=x,则∠AEF=∠1=∠FEA′=x,
∴3x=180°,
∴x=60°,
∴∠AEF=x=60°,
故选:A.
5.C
解:A、平行四边形不是轴对称图形,故本选项不合题意;
B、直角梯形不是轴对称图形,故本选项不合题意;
C、正五边形是轴对称图形,故本选项符合题意;
D、直角三角形不是轴对称图形,故本选项不合题意.
故选:C.
6.B
解:根据折叠的性质,∠A=∠3,∠ADE=∠FDE,∠AED=∠FED,
∵△ABC为等腰直角三角形,∠C=90°,
∴∠A=∠B=∠3=45°,
∴∠3+∠B=90°,故选项③正确;
设∠ADE=∠FDE=,∠AED=∠FED=,
则∠1+∠ADE+∠FDE=∠1+=180°①,∠2+∠AED+∠FED
=∠2+=180°②,
∠A+180°,
①+②得:∠1++∠2+=∠1+∠2+=
360°,
∴∠1+∠2=90°,故选项②正确;
由于∠1+∠2=90°,∠1与∠2不一定相等,故选项①不一定正确;
由于点F在BC边上,不固定,DF与AB不一定平行,故选项④不一定正确;
∴一定正确的是②③,共2个,
故选:B.
.
7.D
解:四边形BEFD是以DE为对称轴的线对称图形,四边形CFDE是以FE为对称轴的线对称图形,
,,
,
故选:D.
8.B
解:连接,如图,
∵是P关于直线l的对称点,
∴直线l是的垂直平分线,
∴
∵是P关于直线m的对称点,
∴直线m是的垂直平分线,
∴
当不在同一条直线上时,
即
当在同一条直线上时,
故选:B
9.C
解:,
,
翻折,
,,
,
,
故选:C.
10.C
解:如图,
如图,设直线与分别交于点,点,
令与的交点为,且,
沿直线翻折,点落在点上,
,
在中,,
在中,,
,
,
即
故选:C.
11.A
解:∵点B坐标为(4,5)
向下平移2个单位,得点B对应点的坐标B1(4,5-2),即B1(4,3),
再沿y轴翻折,
点B′(-4,3),
故选择A.
12.D
解:∵△ABD与△ADB’关于直线AD对称,
∴
∵∠BAC=90°,∠B’AC=14°
∴
∴
∴
故选D.
13.B
观察图形可知与成轴对称的是图形.
故选:B.
14.B
解:∵与关于直线l对称,
∴△ABC≌△A′B′C′,
∴∠A=∠A′=25°,
∵∠B=110°,
∴∠C=180°?∠B?∠A=180°?25°?110°=45°.
故选B.
15.D
解:根据轴对称的性质可知,台球走过的路径为:
∴球最后将落入的球袋是4号袋,
故选:D.
16.100
解:如图,作点A关于BC的对称点A′,关于CD的对称点A″,
连接A′A″与BC、CD的交点即为所求的点M、N,
此时,AM+AN+MN=
A′M+A″N+MN=
A′A″,即周长最小值即为A′A″,
∵∠BAD=130°,∠B=∠D=90°,
∴∠A′+∠A″=180°-∠130°=50°,
由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,
∴∠AMN+∠ANM=2(∠A′+∠A″)=2×50°=100°.
故答案为:100.
17.4
解:根据轴对称的性质可知,台球走过的路径为:
故答案为:4.
18.5.
解:五角星的对称轴共有5条,
故答案为:5.
19.140°
解:连接OP,如图:
∵E,F分别是点P关于OA,OB的对称点,
∴
∵
∴
∵E,F分别是点P关于OA,OB的对称点,
∴
∵
∴
∴
故答案为:140°
20.126°
解:在图1中,∠AEC=36°,
∵AD∥BC,
∴∠BCE=180°-∠AEC=144°,
由折叠可知:∠ECD=(180°-144°)÷2=18°,
∴∠CDE=∠AEC-∠ECD=18°,
∵∠DEF=∠AEC=36°,
∴∠EDG=180°-36°=144°,
在图2中,∠CDG=∠EDG-∠CDE=126°,
故答案为:126°.
21.详见解析.
解:图①中,过点A和BC,EF的交点作直线l;图②中,过BC,EF延长线的交点和AC,DF延长线的交点作直线l.
22.120°
解:因为AD∥BC(已知),
所以∠DEF=∠EFG=30°(两直线平行,内错角相等),
因为∠GEF=∠DEF=30°(对折后重合部分相等),
所以∠DEG=2∠DEF=60°,
所以∠EGC=180°-∠DEG=180°-60°=120°(两直线平行,同旁内角互补).
23.见解析
如图所示:运动路线:.
24.(1)3;(2)①-1;②3.5或-5.5
解:(1)沿过原点且垂直于数轴的直线折叠纸条,则表示-3的点与表示3的点重合;
故答案为:3;
(2)①∵表示-3的点与表示1的点重合,
∴点表示的数是.
②∵,点表示的数是-1,
∴点表示的数是或.
25.(1)
、、;(2)5;
(1)由题知点关于y对称的点为,由对称性质可得:点的坐标:;
同理可得点于x对称的点为,由对称性质可得:点的坐标:;
又AC的垂直平分线为:y=2,与y轴的交点为D,∴
点;
(2)将补为直角梯形,如下图所示:
∴
;;
;
∴;
轴对称
一、单选题
1.下列图形中,是轴对称图形的是( )
A.
B.
C.
D.
2.点关于轴的对称点的坐标为(
).
A.
B.
C.
D.
3.如图,在长方形纸片中,,将长方形纸片沿折叠,点落在点处,交边于点,若,则等于(
)
A.
B.
C.
D.
4.如图,为一长条形纸带,,将沿折叠,、两点分别与、对应,若,则的度数为(
)
A.60°
B.65°
C.72°
D.75°
5.下列图形中,是轴对称图形的是( )
A.平行四边形
B.直角梯形
C.正五边形
D.直角三角形
6.如图,为等腰直角三角形,、将按如图方式进行折叠,使点A与边上的点F重合,折痕分别与、交于点D、点E.下列结论:①;②;③;④.其中一定正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
7.如图,中,D、E、F三点分别在AB、BC、AC上,且四边形BEFD是以DE为对称轴的线对称图形,四边形CFDE是以FE为对称轴的线对称图形若,则的度数为何?(
)
A.65
B.70
C.75
D.80
8.如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是(
)
A.0
B.5
C.6
D.7
9.如图,在中,,沿图中虚线翻折,使得点B落在上的点D处,则等于(
)
A.160°
B.150°
C.140°
D.110°
10.如图,在中,,将沿直线翻折,点落在点的位置,则的度数是(
)
A.
B.
C.
D.
11.是网格中的格点三角形(三角形的各顶点都在网格的交叉点上),如图建立直角坐标系,将该三角形先向下平移2个单位,然后再将平移后的图形沿y轴翻折,得到,则点B对应点的坐标为(
)
A.
B.
C.
D.
12.如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为D,△ABD与△ADB’关于直线AD对称,点B的对称点是点B’,若∠B’AC=14°,则∠B的度数为
(
)
A.38°
B.48°
C.50°
D.52°
13.在下列画的四个三角形中,与成轴对称的是( )
A.
B.
C.
D.
14.如图,已知与关于直线l对称,,则的度数为(
)
A.
B.
C.
D.
15.如图是一个经过改造的规则为的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是(
)
A.1号袋
B.2号袋
C.3号袋
D.4号袋
二、填空题
16.如图,在四边形中,,,在、上分别取一点、,使的周长最小,则___°.
17.如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多反射),则该球最后将落入的球袋是_______.
18.如图所示的五角星是轴对称图形,它的对称轴共有_____条.
19.如图,点P在内部,点E,F分别是点P关于直线,的对称点,若,则______.
20.如图,将长方形纸片沿折叠,交于点E,得到图1,再将纸片沿折叠.得到图2,若,则图2中的为_______
三、解答题
21.如图,三角形ABC与三角形DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
22.手工制作课上,老师先将一张长方形纸片折叠成如图所示的那样,若折痕与一条边BC的夹角∠EFB=30°,你能说出∠EGF的度数吗?
23.已知:如图,是一个长方形的台球面,有、两球分别位于图中所在位置,试问怎样撞击球,才能使先碰到台边反弹后再击中球?在图中画出球的运动线路.
24.如图,已知在一张纸条上画有一条数轴.
(1)沿过原点且垂直于数轴的直线折叠纸条,则表示-3的点与表示___________的点重合;
(2)为数轴上一点,沿过点且垂直于数轴的直线折叠纸条,当表示-3的点与表示1的点重合时,
①点所表示的数为__________;
②若数轴上的,两点也同时重合,且,求点所表示的数.
25.如图,在平面直角坐标系中,A
(-1,
4),
B(3,
2),
C(-1,0)
(1)
点A关于y轴的对称点的坐标为
,点B关于x轴的对称点的坐标为
,
线段AC的垂直平分线与y轴的交点D的坐标为
.
(2)求(1)中的△的面积.
参考答案
1.B
解:A.不是轴对称图形,不符合题意;
B.是轴对称图形,符合题意;
C.不是轴对称图形,不符合题意;
D.不是轴对称图形,不符合题意.
故选:B.
2.A
解:点坐标关于轴对称的变换规律:横坐标变为相反数,纵坐标不变,
则点关于轴的对称点的坐标为,
故选:A.
3.D
解:由折叠的性质得∠ADB=∠EDB,
∴∠ADF=2∠ADB,
∵∠ADB=20°,
∴∠ADF=2×20°=40°,
∵AD∥BC,
∴∠DFC=∠ADF=40°,
故选:D.
4.A
解:由翻折的性质可知:∠AEF=∠FEA′,
∵AB∥CD,
∴∠AEF=∠1,
∵∠1=∠2,设∠2=x,则∠AEF=∠1=∠FEA′=x,
∴3x=180°,
∴x=60°,
∴∠AEF=x=60°,
故选:A.
5.C
解:A、平行四边形不是轴对称图形,故本选项不合题意;
B、直角梯形不是轴对称图形,故本选项不合题意;
C、正五边形是轴对称图形,故本选项符合题意;
D、直角三角形不是轴对称图形,故本选项不合题意.
故选:C.
6.B
解:根据折叠的性质,∠A=∠3,∠ADE=∠FDE,∠AED=∠FED,
∵△ABC为等腰直角三角形,∠C=90°,
∴∠A=∠B=∠3=45°,
∴∠3+∠B=90°,故选项③正确;
设∠ADE=∠FDE=,∠AED=∠FED=,
则∠1+∠ADE+∠FDE=∠1+=180°①,∠2+∠AED+∠FED
=∠2+=180°②,
∠A+180°,
①+②得:∠1++∠2+=∠1+∠2+=
360°,
∴∠1+∠2=90°,故选项②正确;
由于∠1+∠2=90°,∠1与∠2不一定相等,故选项①不一定正确;
由于点F在BC边上,不固定,DF与AB不一定平行,故选项④不一定正确;
∴一定正确的是②③,共2个,
故选:B.
.
7.D
解:四边形BEFD是以DE为对称轴的线对称图形,四边形CFDE是以FE为对称轴的线对称图形,
,,
,
故选:D.
8.B
解:连接,如图,
∵是P关于直线l的对称点,
∴直线l是的垂直平分线,
∴
∵是P关于直线m的对称点,
∴直线m是的垂直平分线,
∴
当不在同一条直线上时,
即
当在同一条直线上时,
故选:B
9.C
解:,
,
翻折,
,,
,
,
故选:C.
10.C
解:如图,
如图,设直线与分别交于点,点,
令与的交点为,且,
沿直线翻折,点落在点上,
,
在中,,
在中,,
,
,
即
故选:C.
11.A
解:∵点B坐标为(4,5)
向下平移2个单位,得点B对应点的坐标B1(4,5-2),即B1(4,3),
再沿y轴翻折,
点B′(-4,3),
故选择A.
12.D
解:∵△ABD与△ADB’关于直线AD对称,
∴
∵∠BAC=90°,∠B’AC=14°
∴
∴
∴
故选D.
13.B
观察图形可知与成轴对称的是图形.
故选:B.
14.B
解:∵与关于直线l对称,
∴△ABC≌△A′B′C′,
∴∠A=∠A′=25°,
∵∠B=110°,
∴∠C=180°?∠B?∠A=180°?25°?110°=45°.
故选B.
15.D
解:根据轴对称的性质可知,台球走过的路径为:
∴球最后将落入的球袋是4号袋,
故选:D.
16.100
解:如图,作点A关于BC的对称点A′,关于CD的对称点A″,
连接A′A″与BC、CD的交点即为所求的点M、N,
此时,AM+AN+MN=
A′M+A″N+MN=
A′A″,即周长最小值即为A′A″,
∵∠BAD=130°,∠B=∠D=90°,
∴∠A′+∠A″=180°-∠130°=50°,
由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,
∴∠AMN+∠ANM=2(∠A′+∠A″)=2×50°=100°.
故答案为:100.
17.4
解:根据轴对称的性质可知,台球走过的路径为:
故答案为:4.
18.5.
解:五角星的对称轴共有5条,
故答案为:5.
19.140°
解:连接OP,如图:
∵E,F分别是点P关于OA,OB的对称点,
∴
∵
∴
∵E,F分别是点P关于OA,OB的对称点,
∴
∵
∴
∴
故答案为:140°
20.126°
解:在图1中,∠AEC=36°,
∵AD∥BC,
∴∠BCE=180°-∠AEC=144°,
由折叠可知:∠ECD=(180°-144°)÷2=18°,
∴∠CDE=∠AEC-∠ECD=18°,
∵∠DEF=∠AEC=36°,
∴∠EDG=180°-36°=144°,
在图2中,∠CDG=∠EDG-∠CDE=126°,
故答案为:126°.
21.详见解析.
解:图①中,过点A和BC,EF的交点作直线l;图②中,过BC,EF延长线的交点和AC,DF延长线的交点作直线l.
22.120°
解:因为AD∥BC(已知),
所以∠DEF=∠EFG=30°(两直线平行,内错角相等),
因为∠GEF=∠DEF=30°(对折后重合部分相等),
所以∠DEG=2∠DEF=60°,
所以∠EGC=180°-∠DEG=180°-60°=120°(两直线平行,同旁内角互补).
23.见解析
如图所示:运动路线:.
24.(1)3;(2)①-1;②3.5或-5.5
解:(1)沿过原点且垂直于数轴的直线折叠纸条,则表示-3的点与表示3的点重合;
故答案为:3;
(2)①∵表示-3的点与表示1的点重合,
∴点表示的数是.
②∵,点表示的数是-1,
∴点表示的数是或.
25.(1)
、、;(2)5;
(1)由题知点关于y对称的点为,由对称性质可得:点的坐标:;
同理可得点于x对称的点为,由对称性质可得:点的坐标:;
又AC的垂直平分线为:y=2,与y轴的交点为D,∴
点;
(2)将补为直角梯形,如下图所示:
∴
;;
;
∴;
