2021--2022学年青岛版八年级数学上册2.6等腰三角形 课件(24张PPT)
文档属性
| 名称 | 2021--2022学年青岛版八年级数学上册2.6等腰三角形 课件(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 13:11:13 | ||
图片预览



文档简介
(共24张PPT)
2.6
等腰三角形
2、等腰三角形的性质?
1、什么是等腰三角形?
两边相等
两边相等,轴对称图形,三线合一
等腰三角线的两个底角相等。
1.探索等腰三角形的判定方法.
2.探索等腰三角形的判定进行简单
推理、判断、应用.
学习目标
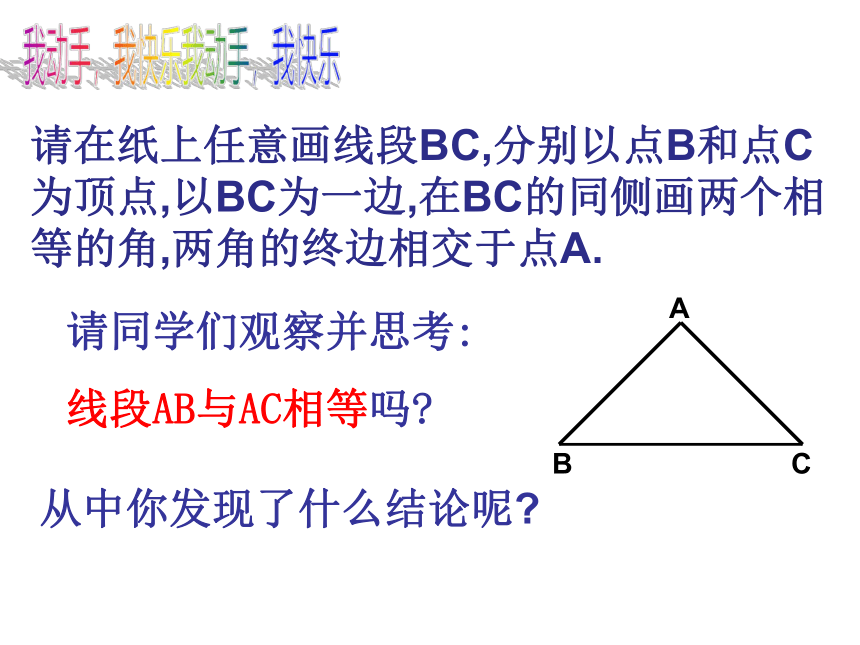
请在纸上任意画线段BC,分别以点B和点C为顶点,以BC为一边,在BC的同侧画两个相等的角,两角的终边相交于点A.
请同学们观察并思考:
线段AB与AC相等吗?
从中你发现了什么结论呢?
B
C
A
大胆猜想:
我的结论是:
有两个角相等的三角形是等腰三角形.
我们猜想的结论一定正确吗?
A
B
C
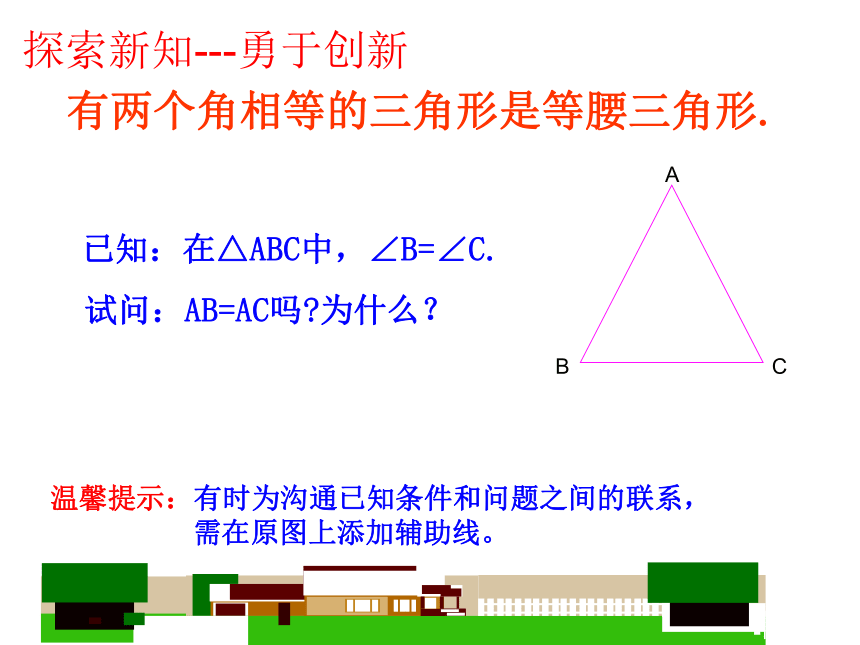
已知:在△ABC中,∠B=∠C.
试问:AB=AC吗?为什么?
探索新知---勇于创新
温馨提示:有时为沟通已知条件和问题之间的联系,
需在原图上添加辅助线。
有两个角相等的三角形是等腰三角形.
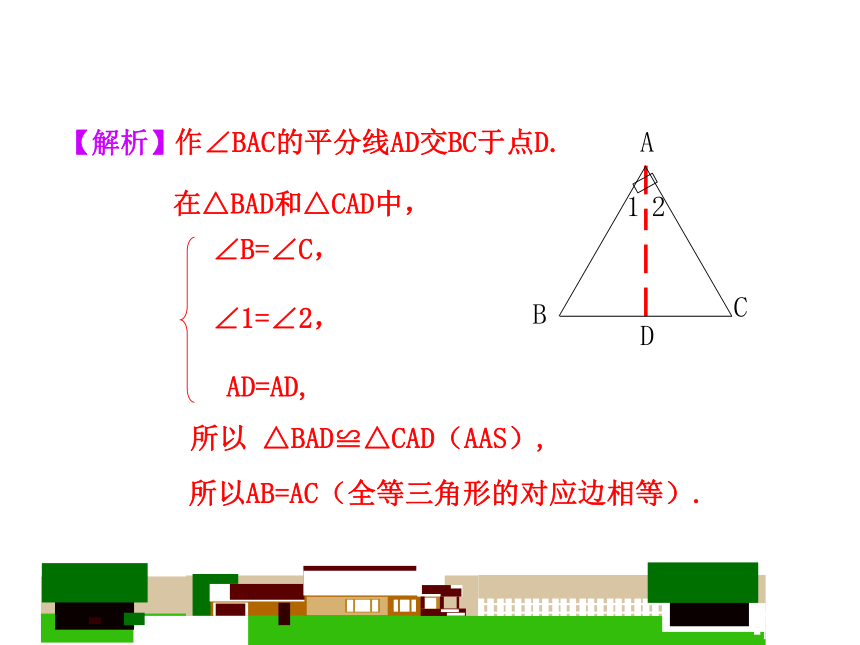
【解析】
作∠BAC的平分线AD交BC于点D.
在△BAD和△CAD中,
∠B=∠C,
∠1=∠2,
AD=AD,
所以
△BAD≌△CAD(AAS),
所以AB=AC(全等三角形的对应边相等).
1
A
B
C
D
2
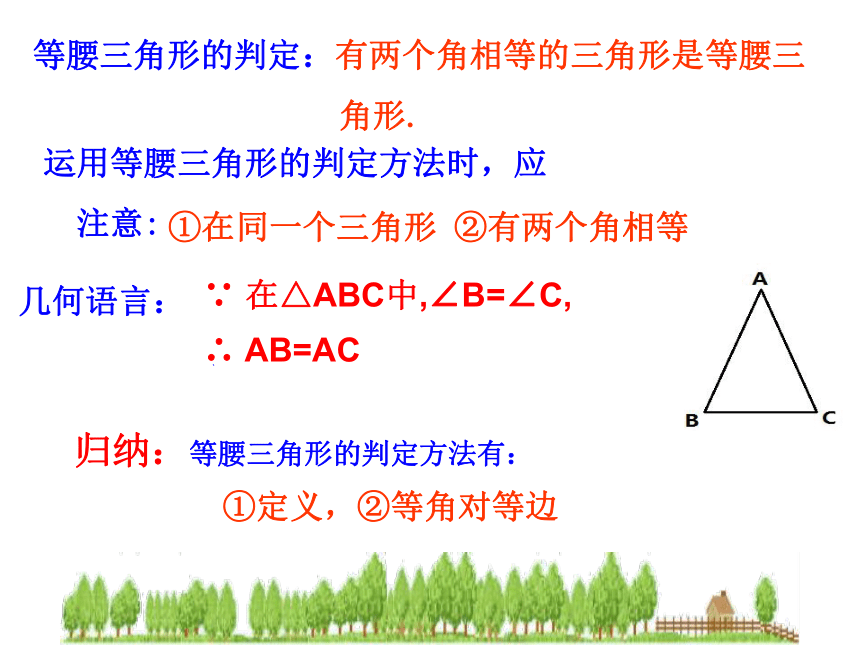
①定义,②等角对等边
①在同一个三角形
②有两个角相等
归纳:等腰三角形的判定方法有:
运用等腰三角形的判定方法时,应
注意:
等腰三角形的判定:有两个角相等的三角形是等腰三
角形.
几何语言:
∴
AB=AC
∵
在△ABC中,∠B=∠C,
学以致用:
1、辨一辨:如图,下列推理正确吗?
2、在△ABC中,∠B=70°,∠C=40°,
则△ABC是
三角形.
3、在△ABC中,∠A:∠B:∠C=4:7:7,
则△ABC是
三角形.
4、在△ABC中,∠B=∠C,AB=3cm,AC=
.
等腰
等腰
3cm
例3
如图,已知∠A=36°,∠DBC=36°,∠C=72°.求∠BDC和∠ABD的度数,并指出图中有哪些等腰三角形?
我一定行:
解:在△DBC中
∵∠DBC=36°∠C=72°,
∴∠BDC=180°—(∠DBC+∠C)
=180°—(36°+72°)=72°
∵
∠BDC=∠A+∠ABD,
∴
∠ABD=∠BDC—∠A=72°—36°=36°
∴
∠A=∠ABD=36°
∴
△ABD是等腰三角形;
∵
∠BDC=∠C=72°
∴△DBC是等腰三角形;
∵∠ABC=∠ABD+∠DBC=36°+36°=72°
∠C=
72°
∴
∠ABC=
∠C
∴△ABC是等腰三角形。
例4
如图,在△ABC中,AB=AC,∠ABC与∠ACB的平分线交于点F,△FBC是等腰三角形吗?为什么?
如图,把一张长方形形的纸沿对角线折叠.
重合部分是一个等腰三角形吗?为什么?
练习1
3
A
B
C
D
E
已知:如图,∠DAC
是△ABC
的一个外角,
AE平分∠DAC,且AE∥BC.
试说明:△ABC是等腰三角形.
练习2
解:
∵AE平分∠DAC,
∴∠DAE
=
∠EAC,
∵AE∥BC,
∴∠DAE=∠B,∠EAC=
∠C,
∴∠B
=
∠C,
∴AB
=
AC.
∴△ABC是等腰三角形.
3
A
B
C
D
E
寻找规律
角平分线+平行线
等腰三角形
2、运用等腰三角形的判定方法时,应注意:
1、等腰三角形的两种判定方法
.
①定义:两边相等的三角形是等
腰三角形;
②判定:有两个角相等的三角形
是等腰三角形。
通过本课时的学习,我们掌握:
3、角平分线+平行线
等腰三角形
两个相等的角须在同一个三角形。
挑战自我:
(1)图1,在△ABC中,AB=AC,∠ABC、∠ACB的平分线相交于点F,如果过点F作底边BC的平行线交AB于点D,交AC于点E,除△ABC和△FBC外,图中还有哪些三角形是等腰三角形?
(2)在(1)中,如果△ABC中,AB、AC不相等,其他条件不变,图中有等腰三角形吗?说明你的理由。
温馨提示:
角平分线+平行线
等腰三角形
作业:
必做:
课后练习:第1题
习题
2.6:
第1题、
选做:
习题2.6:第8题
1、如图所示,量出AC的长,就可知道河的宽度AB,你知道为什么吗?
达标检测
2.(宁波·中考)如图,在△ABC中,AB=AC,∠A=36°,
BD,CE分别是∠ABC、∠BCD的平分线,则图中的等腰三角
形有(
)
B
C
A
D
E
A.5个
B.4个
C.3个
D.2个
【解析】选A.因为
所以∠ABC=∠ACB=72°.
由BD,CE分别是∠ABC,∠BCD的平分线,可得∠ABD=∠CBD=∠ECB=∠ACE=36°.
所以△ABC,△BCD,△ABD,△BCE,△DCE都为等
腰三角形.
∠A=36°,
2、如图,在海上A,B两处有两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
O
B
A
能同时赶到
海到天边天作岸,山登绝顶我为峰。
BD=CD,AD⊥BC
1、如图,在△ABC中,AB=AC,·
(1)若AD平分∠BAC,那么____________________;
(2)若BD=CD,那么_________________________;
(3)若AD⊥BC,那么__________________________.
2、∵
在△ABC中,AB=AC
∴
∠___
=∠___
AD平分∠BAC,AD⊥BC
AD平分∠BAC,BD=CD
B
C
2.6
等腰三角形
2、等腰三角形的性质?
1、什么是等腰三角形?
两边相等
两边相等,轴对称图形,三线合一
等腰三角线的两个底角相等。
1.探索等腰三角形的判定方法.
2.探索等腰三角形的判定进行简单
推理、判断、应用.
学习目标
请在纸上任意画线段BC,分别以点B和点C为顶点,以BC为一边,在BC的同侧画两个相等的角,两角的终边相交于点A.
请同学们观察并思考:
线段AB与AC相等吗?
从中你发现了什么结论呢?
B
C
A
大胆猜想:
我的结论是:
有两个角相等的三角形是等腰三角形.
我们猜想的结论一定正确吗?
A
B
C
已知:在△ABC中,∠B=∠C.
试问:AB=AC吗?为什么?
探索新知---勇于创新
温馨提示:有时为沟通已知条件和问题之间的联系,
需在原图上添加辅助线。
有两个角相等的三角形是等腰三角形.
【解析】
作∠BAC的平分线AD交BC于点D.
在△BAD和△CAD中,
∠B=∠C,
∠1=∠2,
AD=AD,
所以
△BAD≌△CAD(AAS),
所以AB=AC(全等三角形的对应边相等).
1
A
B
C
D
2
①定义,②等角对等边
①在同一个三角形
②有两个角相等
归纳:等腰三角形的判定方法有:
运用等腰三角形的判定方法时,应
注意:
等腰三角形的判定:有两个角相等的三角形是等腰三
角形.
几何语言:
∴
AB=AC
∵
在△ABC中,∠B=∠C,
学以致用:
1、辨一辨:如图,下列推理正确吗?
2、在△ABC中,∠B=70°,∠C=40°,
则△ABC是
三角形.
3、在△ABC中,∠A:∠B:∠C=4:7:7,
则△ABC是
三角形.
4、在△ABC中,∠B=∠C,AB=3cm,AC=
.
等腰
等腰
3cm
例3
如图,已知∠A=36°,∠DBC=36°,∠C=72°.求∠BDC和∠ABD的度数,并指出图中有哪些等腰三角形?
我一定行:
解:在△DBC中
∵∠DBC=36°∠C=72°,
∴∠BDC=180°—(∠DBC+∠C)
=180°—(36°+72°)=72°
∵
∠BDC=∠A+∠ABD,
∴
∠ABD=∠BDC—∠A=72°—36°=36°
∴
∠A=∠ABD=36°
∴
△ABD是等腰三角形;
∵
∠BDC=∠C=72°
∴△DBC是等腰三角形;
∵∠ABC=∠ABD+∠DBC=36°+36°=72°
∠C=
72°
∴
∠ABC=
∠C
∴△ABC是等腰三角形。
例4
如图,在△ABC中,AB=AC,∠ABC与∠ACB的平分线交于点F,△FBC是等腰三角形吗?为什么?
如图,把一张长方形形的纸沿对角线折叠.
重合部分是一个等腰三角形吗?为什么?
练习1
3
A
B
C
D
E
已知:如图,∠DAC
是△ABC
的一个外角,
AE平分∠DAC,且AE∥BC.
试说明:△ABC是等腰三角形.
练习2
解:
∵AE平分∠DAC,
∴∠DAE
=
∠EAC,
∵AE∥BC,
∴∠DAE=∠B,∠EAC=
∠C,
∴∠B
=
∠C,
∴AB
=
AC.
∴△ABC是等腰三角形.
3
A
B
C
D
E
寻找规律
角平分线+平行线
等腰三角形
2、运用等腰三角形的判定方法时,应注意:
1、等腰三角形的两种判定方法
.
①定义:两边相等的三角形是等
腰三角形;
②判定:有两个角相等的三角形
是等腰三角形。
通过本课时的学习,我们掌握:
3、角平分线+平行线
等腰三角形
两个相等的角须在同一个三角形。
挑战自我:
(1)图1,在△ABC中,AB=AC,∠ABC、∠ACB的平分线相交于点F,如果过点F作底边BC的平行线交AB于点D,交AC于点E,除△ABC和△FBC外,图中还有哪些三角形是等腰三角形?
(2)在(1)中,如果△ABC中,AB、AC不相等,其他条件不变,图中有等腰三角形吗?说明你的理由。
温馨提示:
角平分线+平行线
等腰三角形
作业:
必做:
课后练习:第1题
习题
2.6:
第1题、
选做:
习题2.6:第8题
1、如图所示,量出AC的长,就可知道河的宽度AB,你知道为什么吗?
达标检测
2.(宁波·中考)如图,在△ABC中,AB=AC,∠A=36°,
BD,CE分别是∠ABC、∠BCD的平分线,则图中的等腰三角
形有(
)
B
C
A
D
E
A.5个
B.4个
C.3个
D.2个
【解析】选A.因为
所以∠ABC=∠ACB=72°.
由BD,CE分别是∠ABC,∠BCD的平分线,可得∠ABD=∠CBD=∠ECB=∠ACE=36°.
所以△ABC,△BCD,△ABD,△BCE,△DCE都为等
腰三角形.
∠A=36°,
2、如图,在海上A,B两处有两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
O
B
A
能同时赶到
海到天边天作岸,山登绝顶我为峰。
BD=CD,AD⊥BC
1、如图,在△ABC中,AB=AC,·
(1)若AD平分∠BAC,那么____________________;
(2)若BD=CD,那么_________________________;
(3)若AD⊥BC,那么__________________________.
2、∵
在△ABC中,AB=AC
∴
∠___
=∠___
AD平分∠BAC,AD⊥BC
AD平分∠BAC,BD=CD
B
C
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
