2021-2022学年湘教版数学九年级上册3.4.1相似三角形的判定1 同步课件(17张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册3.4.1相似三角形的判定1 同步课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 517.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览




文档简介
第三章 图形的相似
3.4.1 相似三角形的判定
第1课时 相似三角形判定的基本定理
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
A
B
C
C '
B '
A '
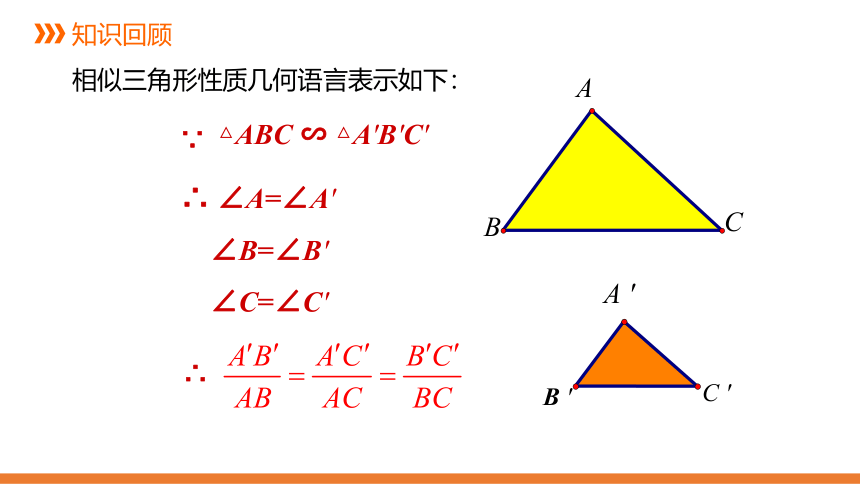
△ABC ∽ △A'B'C'
∵
∴ ∠A=∠A'
∠B=∠B'
∠C=∠C'
∴
相似三角形性质几何语言表示如下:
A
B
C
C'
B'
A'
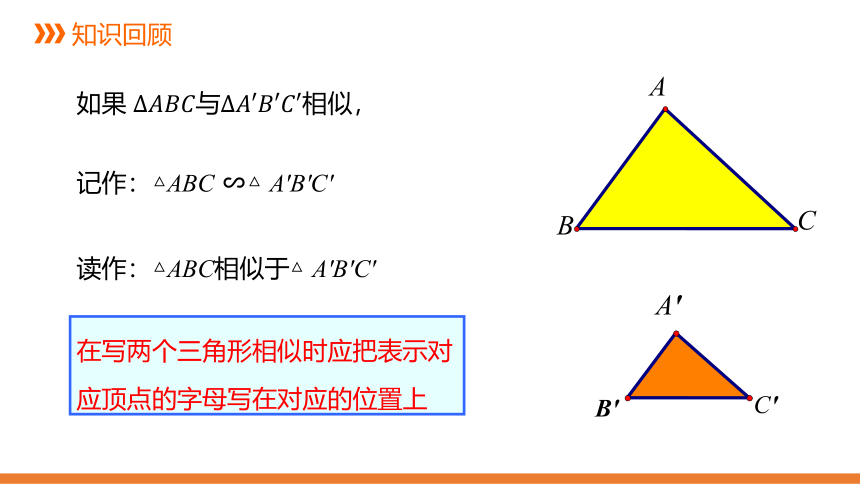
如果 Δ????????????与Δ????′????′????′相似,
?
记作:△ABC ∽△ A'B'C'
读作:△ABC相似于△ A'B'C'
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上
定义
判定方法
全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等, 三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边与直角边
H
L
判定三角形相似,是不是也有这么多种方法呢?
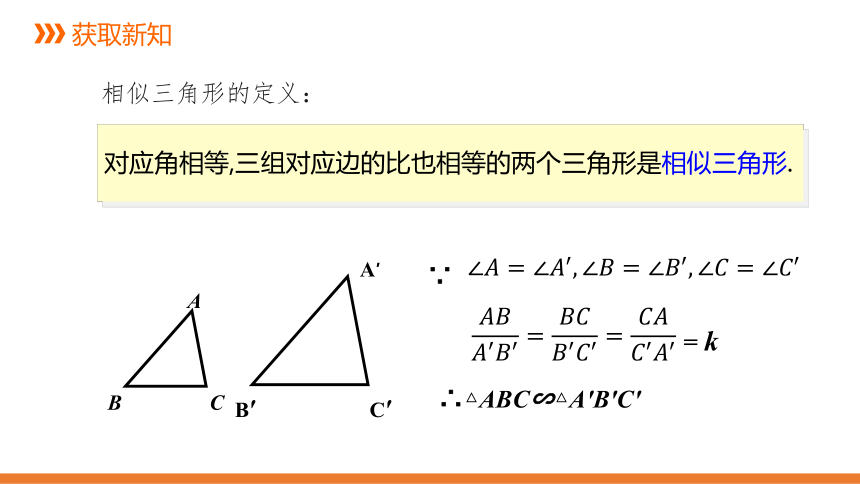
相似三角形的定义:
对应角相等,三组对应边的比也相等的两个三角形是相似三角形.
A
C′
B′
A′
C
B
= k
∴△ABC∽△A'B'C'
?????????????′????′=????????????′????′=????????????′????′
?
?∠????=∠????′,∠????=∠????′,∠????=∠????′
?
∵
如图, 在ΔABC中,D为AB上任意一点.过点D作BC的平行线DE , 交AC于点E.
(1)ΔADE 与ΔABC 的三个角分别相等吗?
(2)分别度量ΔADE与ΔABC的边长,它们的边长是否对应成比例?
(3)ΔADE与ΔABC 之间有什么关系?平行移动DE的位置,你的结论还成立吗?
?
我发现只要DE//BC,那么ΔADE与Δ?ABC是相似的
?
A
B
C
D
E
如图, 在ΔABC中,D为AB上任意一点.过点D作BC的平行线DE , 交AC于点E.
(1)ΔADE 与ΔABC 的三个角分别相等吗?
(2)分别度量ΔADE与ΔABC的边长,它们的边长是否对应成比例?
(3)ΔADE与ΔABC 之间有什么关系?平行移动DE的位置,你的结论还成立吗?
?
在ΔADE 与ΔABC中, ∠????=∠????
∵ DE//BC,
∴∠????????????=∠????, ∠????????????=∠????.
?
A
B
C
D
E
公共角
两直线平行
同位角相等
如图, 在ΔABC中,D为AB上任意一点.过点D作BC的平行线DE , 交AC于点E.
(1)ΔADE 与ΔABC 的三个角分别相等吗?
(2)分别度量ΔADE与ΔABC的边长,它们的边长是否对应成比例?
(3)ΔADE与ΔABC 之间有什么关系?平行移动DE的位置,你的结论还成立吗?
?
过点D作DF//AC,交BC于点F
∵ DE//BC ,DF//AC,
∴ ????????????????=???????????????? , ????????????????=???????????????? .
?
A
B
C
D
E
F
∵四边形DFCE为平行四边形,
∴ DE=FC,
∴ ????????????????=????????????????= ????????????????.
∴ ΔADE ∽ ΔABC
?
平行线分线段成比例
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
你还能画出其他图形吗?
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
你还能画出其他图形吗?
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
D
E
A
C
B
如果DE∥BC,
那么△ADE∽△ACB.
例1:在△ABC中,已知点D,E分别是AB,AC边的中点.
求证: △ ADE∽△ ABC.
证明:
∵点????,????分别是????????,????????边的中点,
∴????????∥BC,
∴ ΔADE ∽ ΔABC.
?
A
B
C
D
E
例2:点D为△ABC的边AB的中点,过点D作DE ∥ BC交AB于点E.延长DE至点F,使DE=EF.
求证:△BFE∽△ ACB.
证明:
∵DE // BC,
点????是????????????????的边????????的中点,∴????????=????????.又????????=????????,∠????????????=∠????????????,∴?????????????????????????????????.
∵DE // BC,
∴△ ADE∽△ ACB.
∴△ BFE∽△ ACB.
?
A
B
C
D
E
F
知识点:判定三角形相似的预备定理(平行截相似)
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形 .?
[点拨] 平行于三角形一边的直线,与其他两边的延长线相交,截得的三角形与原三角形相似.
相似
3.4.1 相似三角形的判定
第1课时 相似三角形判定的基本定理
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
A
B
C
C '
B '
A '
△ABC ∽ △A'B'C'
∵
∴ ∠A=∠A'
∠B=∠B'
∠C=∠C'
∴
相似三角形性质几何语言表示如下:
A
B
C
C'
B'
A'
如果 Δ????????????与Δ????′????′????′相似,
?
记作:△ABC ∽△ A'B'C'
读作:△ABC相似于△ A'B'C'
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上
定义
判定方法
全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等, 三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边与直角边
H
L
判定三角形相似,是不是也有这么多种方法呢?
相似三角形的定义:
对应角相等,三组对应边的比也相等的两个三角形是相似三角形.
A
C′
B′
A′
C
B
= k
∴△ABC∽△A'B'C'
?????????????′????′=????????????′????′=????????????′????′
?
?∠????=∠????′,∠????=∠????′,∠????=∠????′
?
∵
如图, 在ΔABC中,D为AB上任意一点.过点D作BC的平行线DE , 交AC于点E.
(1)ΔADE 与ΔABC 的三个角分别相等吗?
(2)分别度量ΔADE与ΔABC的边长,它们的边长是否对应成比例?
(3)ΔADE与ΔABC 之间有什么关系?平行移动DE的位置,你的结论还成立吗?
?
我发现只要DE//BC,那么ΔADE与Δ?ABC是相似的
?
A
B
C
D
E
如图, 在ΔABC中,D为AB上任意一点.过点D作BC的平行线DE , 交AC于点E.
(1)ΔADE 与ΔABC 的三个角分别相等吗?
(2)分别度量ΔADE与ΔABC的边长,它们的边长是否对应成比例?
(3)ΔADE与ΔABC 之间有什么关系?平行移动DE的位置,你的结论还成立吗?
?
在ΔADE 与ΔABC中, ∠????=∠????
∵ DE//BC,
∴∠????????????=∠????, ∠????????????=∠????.
?
A
B
C
D
E
公共角
两直线平行
同位角相等
如图, 在ΔABC中,D为AB上任意一点.过点D作BC的平行线DE , 交AC于点E.
(1)ΔADE 与ΔABC 的三个角分别相等吗?
(2)分别度量ΔADE与ΔABC的边长,它们的边长是否对应成比例?
(3)ΔADE与ΔABC 之间有什么关系?平行移动DE的位置,你的结论还成立吗?
?
过点D作DF//AC,交BC于点F
∵ DE//BC ,DF//AC,
∴ ????????????????=???????????????? , ????????????????=???????????????? .
?
A
B
C
D
E
F
∵四边形DFCE为平行四边形,
∴ DE=FC,
∴ ????????????????=????????????????= ????????????????.
∴ ΔADE ∽ ΔABC
?
平行线分线段成比例
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
你还能画出其他图形吗?
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
你还能画出其他图形吗?
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
D
E
A
C
B
如果DE∥BC,
那么△ADE∽△ACB.
例1:在△ABC中,已知点D,E分别是AB,AC边的中点.
求证: △ ADE∽△ ABC.
证明:
∵点????,????分别是????????,????????边的中点,
∴????????∥BC,
∴ ΔADE ∽ ΔABC.
?
A
B
C
D
E
例2:点D为△ABC的边AB的中点,过点D作DE ∥ BC交AB于点E.延长DE至点F,使DE=EF.
求证:△BFE∽△ ACB.
证明:
∵DE // BC,
点????是????????????????的边????????的中点,∴????????=????????.又????????=????????,∠????????????=∠????????????,∴?????????????????????????????????.
∵DE // BC,
∴△ ADE∽△ ACB.
∴△ BFE∽△ ACB.
?
A
B
C
D
E
F
知识点:判定三角形相似的预备定理(平行截相似)
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形 .?
[点拨] 平行于三角形一边的直线,与其他两边的延长线相交,截得的三角形与原三角形相似.
相似
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
