2021-2022学年人教版数学八年级上册11.1.1三角形的边 同步练习题(word版含答案 )
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册11.1.1三角形的边 同步练习题(word版含答案 ) |  | |
| 格式 | docx | ||
| 文件大小 | 157.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 17:04:57 | ||
图片预览

文档简介
107696001136650011.1.1 三角形的边
1.下列结论中,正确的是( )
A.等腰三角形是等边三角形 B.等边三角形是等腰三角形
C.等腰三角形一定是锐角三角形 D.等腰三角形一定是钝角三角形
2.三角形按边分类可分为( )
A.三边都不相等的三角形、等边三角形
B.等腰三角形、等边三角形
C.三边都不相等的三角形、等腰三角形、等边三角形
D.三边都不相等的三角形、等腰三角形
3.下列各组数中,能作为一个三角形三边边长的是( )
A.1、1、2 B.1、2、4 C.2、3、4 D.2、3、5
4.已知三角形两边长分别为3和8,则该三角形第三边的长可能是( )
A.5 B.10 C.11 D.12
5.用集合观点来表示“按边把三角形分类”,下列表示正确的是( )
6.某同学用长分别为5cm、7cm、9cm、13cm的四根木棒摆三角形(用其中三根木棒首尾顺次相接),每摆好一个后,拆开再摆,这样最多可摆出不同的三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
7.已知a、b、c是△ABC的三边长,a、b满足|a-7|+(b-1)2=0,c为奇数,则c等于( )
A.7 B.9 C.11 D.12
8.已知三角形的三边满足|a-b|+(b-c)2=0,则此三角形是 三角形.
9.已知两条线段的长为5cm和8cm,要钉成一个三角形,则第三条线段的长度范围为 .
10.等腰三角形的两边长分别是5和9,则第三边长为 .
11.若等腰三角形的两条边长分别为7cm和14cm,则它的周长为 cm.
12.若等腰三角形的腰长为6,则它的底边长a的取值范围是 .
13. 若等腰三角形的底边长为4,则它的腰长b的取值范围是 .
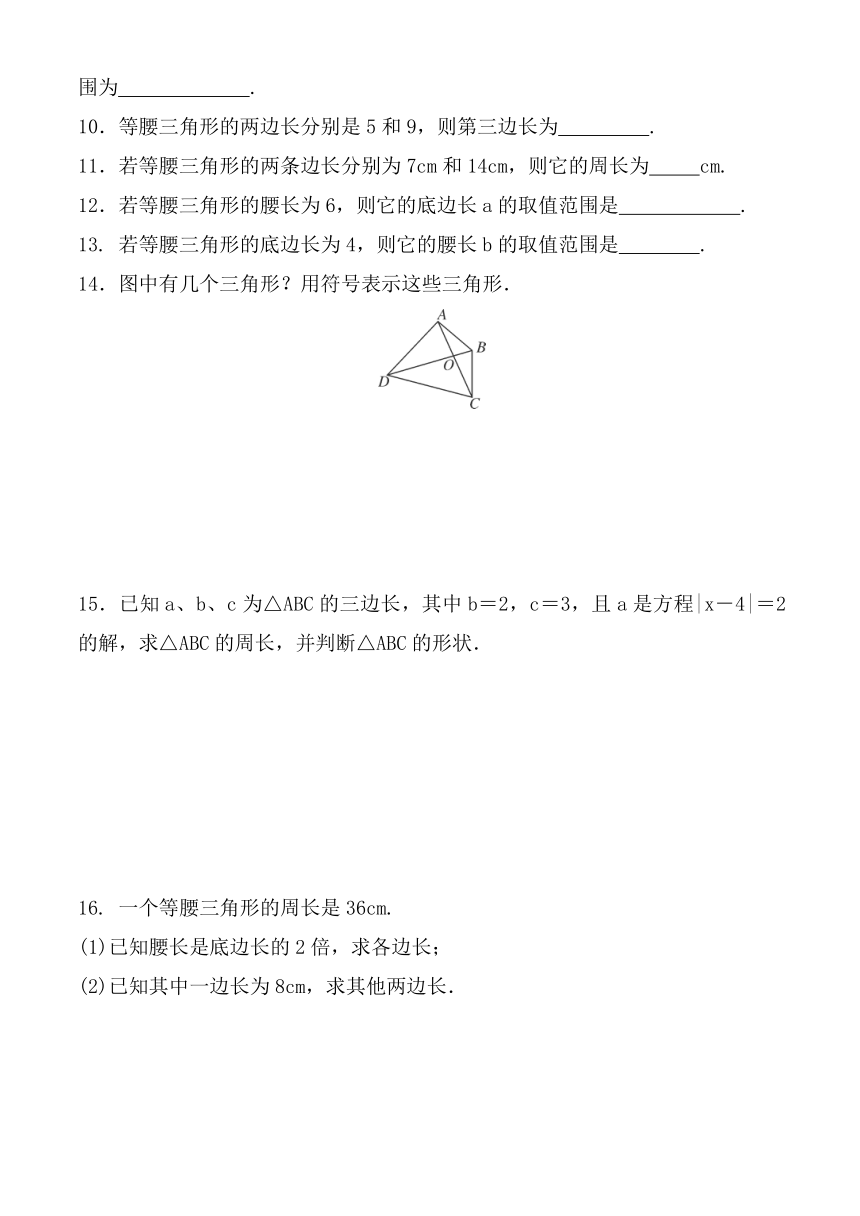
14.图中有几个三角形?用符号表示这些三角形.
15.已知a、b、c为△ABC的三边长,其中b=2,c=3,且a是方程|x-4|=2的解,求△ABC的周长,并判断△ABC的形状.
16. 一个等腰三角形的周长是36cm.
(1)已知腰长是底边长的2倍,求各边长;
(2)已知其中一边长为8cm,求其他两边长.
17.已知:a、b、c是△ABC的三边,且a=4,b=6.若三角形的周长是小于18的偶数.
(1)求c边的长;
(2)判断△ABC的形状.
18.小王准备用一段长30m的篱笆围成一个三角形形状的场地,用于饲养家兔.已知第一条边长为am,由于受地势限制,第二条边长只能比第一条边长的2倍多2m.
(1)请用a表示第三条边长;
(2)第一条边长可以为7m吗?请说明理由.
19.有一条长为22cm的细绳围成一个等腰三角形.
(1)如果腰长比底边长的2倍多1cm,那么各边的长是多少?
(2)能围成一边长为5cm的等腰三角形吗?说明理由.
答案:
1-7 BDCBD CA
8. 等边
9. 3<x<13
10. 5或9
11. 35
12. 0<a<12 13. b>2
14. 解:图中有8个三角形,分别为:△AOD、△AOB、△BOC、△COD、△ABD、△ABC、△BDC、△ADC.
15. 解:因为|x-4|=2,则x-4=±2,解得x=6或x=2,即a=6或a=2,
当a=6时,2+3<6,故a=6不合题意(舍去);当a=2时,a+b+c=2+2+3=7,所以△ABC的周长为2+2+3=7,△ABC为等腰三角形.
16. 解: (1)设底边长为xcm,则腰长为2xcm.x+2x+2x=36,解得x=7.2.所以2x=2×7.2=14.4.所以三边长分别为7.2cm、14.4cm、14.4cm;
(2)若腰长为8cm,则底边长为36-2×8=20(cm).此时8+8<20,故不能组成三角形,所以腰长不能为8cm;若底边长为8cm,则腰长为=14(cm),能构成三角形,所以其他两边长分别为14cm、14cm.
17. 解:(1)因为a=4,b=6,所以周长l的范围为12<l<20,又因为周长是小于18的偶数,所以l=16或14.当周长为16时,c=6;当周长为14时,c=4;
(2)当c=6时,b=c,△ABC为等腰三角形;当c=4时,a=c,△ABC也为等腰三角形.
18. 解:(1)第三条边长为30-a-(2a+2)=(28-3a)m;
(2)第一条边长不可以为7m;
理由:当a=7时,三边分别为7、16、7.∵7+7<16,∴不能构成三角形,即第一条边长不可以为7m.
19. 解:(1)设底边长为xcm,则腰长为(2x+1)cm,x+2x+1+2x+1=22,解得x=4.所以,三边长分别为4cm、9cm、9cm;
(2)若腰长为5cm,则底边长为22-2×5=12cm,因为5+5<12,所以不能围成腰长为5cm的等腰三角形;若底边长为5cm,则腰长为=8.5,能构成三角形,所以能围成底边长为5cm的等腰三角形.
1.下列结论中,正确的是( )
A.等腰三角形是等边三角形 B.等边三角形是等腰三角形
C.等腰三角形一定是锐角三角形 D.等腰三角形一定是钝角三角形
2.三角形按边分类可分为( )
A.三边都不相等的三角形、等边三角形
B.等腰三角形、等边三角形
C.三边都不相等的三角形、等腰三角形、等边三角形
D.三边都不相等的三角形、等腰三角形
3.下列各组数中,能作为一个三角形三边边长的是( )
A.1、1、2 B.1、2、4 C.2、3、4 D.2、3、5
4.已知三角形两边长分别为3和8,则该三角形第三边的长可能是( )
A.5 B.10 C.11 D.12
5.用集合观点来表示“按边把三角形分类”,下列表示正确的是( )
6.某同学用长分别为5cm、7cm、9cm、13cm的四根木棒摆三角形(用其中三根木棒首尾顺次相接),每摆好一个后,拆开再摆,这样最多可摆出不同的三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
7.已知a、b、c是△ABC的三边长,a、b满足|a-7|+(b-1)2=0,c为奇数,则c等于( )
A.7 B.9 C.11 D.12
8.已知三角形的三边满足|a-b|+(b-c)2=0,则此三角形是 三角形.
9.已知两条线段的长为5cm和8cm,要钉成一个三角形,则第三条线段的长度范围为 .
10.等腰三角形的两边长分别是5和9,则第三边长为 .
11.若等腰三角形的两条边长分别为7cm和14cm,则它的周长为 cm.
12.若等腰三角形的腰长为6,则它的底边长a的取值范围是 .
13. 若等腰三角形的底边长为4,则它的腰长b的取值范围是 .
14.图中有几个三角形?用符号表示这些三角形.
15.已知a、b、c为△ABC的三边长,其中b=2,c=3,且a是方程|x-4|=2的解,求△ABC的周长,并判断△ABC的形状.
16. 一个等腰三角形的周长是36cm.
(1)已知腰长是底边长的2倍,求各边长;
(2)已知其中一边长为8cm,求其他两边长.
17.已知:a、b、c是△ABC的三边,且a=4,b=6.若三角形的周长是小于18的偶数.
(1)求c边的长;
(2)判断△ABC的形状.
18.小王准备用一段长30m的篱笆围成一个三角形形状的场地,用于饲养家兔.已知第一条边长为am,由于受地势限制,第二条边长只能比第一条边长的2倍多2m.
(1)请用a表示第三条边长;
(2)第一条边长可以为7m吗?请说明理由.
19.有一条长为22cm的细绳围成一个等腰三角形.
(1)如果腰长比底边长的2倍多1cm,那么各边的长是多少?
(2)能围成一边长为5cm的等腰三角形吗?说明理由.
答案:
1-7 BDCBD CA
8. 等边
9. 3<x<13
10. 5或9
11. 35
12. 0<a<12 13. b>2
14. 解:图中有8个三角形,分别为:△AOD、△AOB、△BOC、△COD、△ABD、△ABC、△BDC、△ADC.
15. 解:因为|x-4|=2,则x-4=±2,解得x=6或x=2,即a=6或a=2,
当a=6时,2+3<6,故a=6不合题意(舍去);当a=2时,a+b+c=2+2+3=7,所以△ABC的周长为2+2+3=7,△ABC为等腰三角形.
16. 解: (1)设底边长为xcm,则腰长为2xcm.x+2x+2x=36,解得x=7.2.所以2x=2×7.2=14.4.所以三边长分别为7.2cm、14.4cm、14.4cm;
(2)若腰长为8cm,则底边长为36-2×8=20(cm).此时8+8<20,故不能组成三角形,所以腰长不能为8cm;若底边长为8cm,则腰长为=14(cm),能构成三角形,所以其他两边长分别为14cm、14cm.
17. 解:(1)因为a=4,b=6,所以周长l的范围为12<l<20,又因为周长是小于18的偶数,所以l=16或14.当周长为16时,c=6;当周长为14时,c=4;
(2)当c=6时,b=c,△ABC为等腰三角形;当c=4时,a=c,△ABC也为等腰三角形.
18. 解:(1)第三条边长为30-a-(2a+2)=(28-3a)m;
(2)第一条边长不可以为7m;
理由:当a=7时,三边分别为7、16、7.∵7+7<16,∴不能构成三角形,即第一条边长不可以为7m.
19. 解:(1)设底边长为xcm,则腰长为(2x+1)cm,x+2x+1+2x+1=22,解得x=4.所以,三边长分别为4cm、9cm、9cm;
(2)若腰长为5cm,则底边长为22-2×5=12cm,因为5+5<12,所以不能围成腰长为5cm的等腰三角形;若底边长为5cm,则腰长为=8.5,能构成三角形,所以能围成底边长为5cm的等腰三角形.
