2021-2022学年人教版八年级数学上册13.3.1 等腰三角形 同步练习 (word版含答案解析 )
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.3.1 等腰三角形 同步练习 (word版含答案解析 ) |  | |
| 格式 | docx | ||
| 文件大小 | 554.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 17:20:26 | ||
图片预览




文档简介
13.3.1 等腰三角形
一、单选题
1.如图,把一张长方形的纸,按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC是( )
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰直角三角形
2.若等腰三角形的周长为false,其中一边长为false,则该等腰三角形的底边为( )
A.false B.false C.false或false D.false
3.如图,AD=BC,AB=AC=BD,∠C=72°,则图中一共有( )个等腰三角形.
A.3 B.4 C.5 D.6
4.已知在平面直角坐标系false中,false点false在false轴或false轴上移动,若false三点可构成等腰三角形,则符合条件的false点有( )
A.false个 B.false个 C.false个 D.false个
5.如图,在false的正方形网格中有两个格点A、B,连接false,在网格中再找一个格点C,使得false是等腰直角三角形,满足条件的格点C的个数是( )
A.2 B.3 C.4 D.5
6.如图,在false中,false和false的角平分线交于点false,过点false作false交false于点false,交false于点false.若false,false,则false的长为( )
A.10 B.5.5 C.6 D.5
7.如图,在false中,false,以点false为圆心,任意长为半径画弧分别交false于点false和false,再分别以false为圆心,大于false的长为半径画弧,两弧交于点false,连接false并延长交false于点false,则下列结论不正确的是( )
A.false是∠BAC的平分线 B.false
C.点false在false的垂直平分线上 D.false
8.如图,已知OC平分∠AOB,false,若CD=3cm,则OD等于( )
A.3cm B.4cm C.1.5cm D.2cm
9.如图,△ABC中,∠B=2∠A,∠ACB的平分线CD交AB于点D,已知AC=16,BC=9,则BD的长为( )
A.6 B.7 C.8 D.9
10.在false中,false于D,false平分false交false于E,则下列结论一定成立的是( )
A.false B.false C.false D.false
11.如图,在false中,false,false,false的垂直平分线false交false于点false,交false于点false,若false,则false的长为( )
A.5 B.8 C.10 D.false
12.如图,在false中,false,false,false,则false的度数为( )
A.12° B.13° C.14° D.15°
二、填空题
13.若(a-4)2+|b-2|=0,则有两边长为a、b的等腰三角形的周长为________.
14.过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为____.
15.如图,在false中,false过点false作false,交false于点false,则false_______________________false.
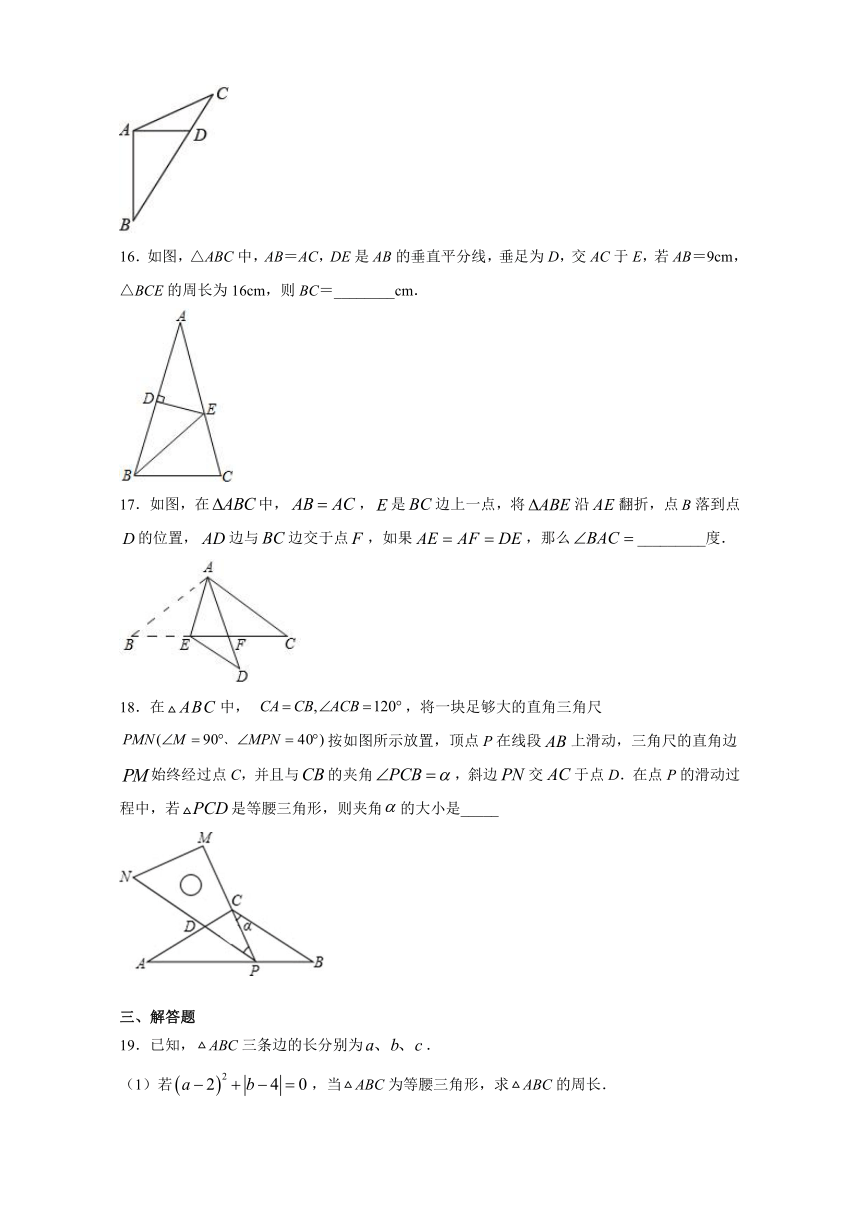
16.如图,△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E,若AB=9cm,△BCE的周长为16cm,则BC=________cm.
17.如图,在false中,false,false是false边上一点,将false沿false翻折,点false落到点false的位置,false边与false边交于点false,如果false,那么false_________度.
18.在false中, false,将一块足够大的直角三角尺false按如图所示放置,顶点P在线段false上滑动,三角尺的直角边false始终经过点C,并且与false的夹角false,斜边false交false于点D.在点P的滑动过程中,若false是等腰三角形,则夹角false的大小是_____
三、解答题
19.已知,falseABC三条边的长分别为false.
(1)若false,当falseABC为等腰三角形,求falseABC的周长.
(2)化简:false.
20.如图,已知false平分false,false,false是false的中点,试说明false的理由,
21.如图,已知在等腰false中false,点D,点E和点F分别是false,false和false边上的点,且false,false,试说明false.
22.如图,在四边形ABCD中,∠B=90°,AC平分∠DAB,DE⊥AC,垂足为E,且AE=AB.
(1)求证:BC=DE;
(2)若∠DAC=40°,求∠CDE的度数.
23.如图,在false中,false的平分线交false于点false,过点false作false;交false于点false.
(1)求证:false;
(2)若false,求false的度数.
24.如图,在false中,false为false的中点,false,false,动点false从点false出发,沿false方向以3个单位长度每秒的速度向点false运动;同时动点false从点false出发,沿false方向以3个单位长度每秒的速度向点false运动,运动时间是false秒.
(1)在运动过程中,当false______秒时,false;
(2)在运动过程中,当false时,求出false的值;
(3)是否存在某一时刻false,使false?若存在,求出false的值;若不存在,请说明理由.
参考答案
1.C
解:由题可得,AB与AC可重合,即AB=AC,
∴△ABC是等腰三角形.
故选:C.
2.B
解:①4cm是底边时,腰长为false×(16-4)=6,能组成三角形,
②4cm是腰长时,底边为16-2×4=8,
∵4+4=8,
∴不能组成三角形,
综上所述,该等腰三角形的底边长为6cm.
故选:B.
3.C
解:∵AB=AC=BD,
∴△ABD与△BAC是等腰三角形,
在△ABD与△BAC中,
false,
∴△ABD≌△BAC(SSS),
∴∠D=∠C=72°,
∴∠BAD=∠D=∠C=∠ABC=72°,
∴∠∠ABD=∠BAC=36°,
∴∠DAE=∠CBE=36°,
∴∠AED=∠BEC=72°,
∴∠D=∠AED=∠C=∠BEC,
∴△ADE和△BCE是等腰三角形,
∵∠AED=∠BEC,
∴△ADE≌△BCE(AAS),
∴AE=BE,
∴△ABE是等腰三角形,
故选:C.
4.B
解:由题意得,false
①分别以点O和点A为圆心,5为半径作弧,交x轴和y轴,于点B1、B2、B5、B6、B7、B8,共6个点;
②AB的垂直平分线x轴和y轴,于点B3和B4,共两个点.
故答案为B.
5.B
解:如图:分情况讨论:
①AB为等腰直角△ABC底边时,符合条件的C点有0个;
②AB为等腰直角△ABC其中的一条腰时,符合条件的C点有3个.
故共有3个点,
故选:B.
6.D
解:∵MN∥BC,
∴∠MEB=∠CBE,∠NEC=∠BCE,
∵在△ABC中,∠ABC和∠ACB的平分线交于点E,
∴∠MBE=∠EBC,∠NCE=∠BCE,
∴∠MEB=∠MBE,∠NEC=∠NCE,
∴ME=MB,NE=NC,
∴MN=ME+NE=BM+CN=2+3=5,
故选:D.
7.D
解:根据作图方法可得false是false的平分线,故A正确;
∵false,
∴false.
∵false是false的平分线,
∴false.
∴false.故B正确;
过D作DE⊥AB
∵false,
∴false.
∴AE=BE
∴点D在false的垂直平分线上.故C正确;
∵false,
∴false,
∵false,
∴false.
∴false,false,
∴false,
∴false,
∴false,故D错误.
故选择:D.
8.A
解:false平分false,
false,
false,
false,
false,
false,
故选:A.
9.B
解:如图,在false上截取false 连接false
false平分false
false
false
false
false
false
false
false
false
false
false
false
false
故选:false
10.D
解:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠A=90°,
∴∠BCD=∠A.
∵CE平分∠ACD,
∴∠ACE=∠DCE.
又∵∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,
∴∠BEC=∠BCE,
∴BC=BE.
故选:D.
11.C
解:∵BC=AB,false,
∴∠C=∠A=36°,
∵false的垂直平分线false交false于点false,交false于点false,
∴AE=BE,
∴∠A=∠ABE=36°,
∴∠BEC=2∠A=72°,
∴∠CBE=180°-72°-36°=72°,
∴∠CBE=∠BEC,
∴CE=BC=AB=10,
故选:C.
12.D
解:如图,过C作CE⊥AD于E,过D作DF⊥BC于F.
∵∠CAD=30°,
∴∠ACE=60°,且CE=falseAC,
∵AC=AD,∠CAD=30°,
∴∠ACD=75°,
∴∠FCD=90°-∠ACD=15°,∠ECD=∠ACD-∠ACE=15°,
在△CED和△CFD中,
false,
∴△CED≌△CFD(AAS),
∴CF=CE=falseAC=falseBC,
∴CF=BF,
∵DF⊥BC,
∴BD=CD,
∴∠DCB=∠CBD=15°,
故选:D.
13.10
解:根据题意得,a-4=0,b-2=0,
解得a=4,b=2,
①若2是腰长,则底边为4,三角形的三边分别为2、2、4,不能组成三角形,
②若4是腰长,则底边为2,三角形的三边分别为4、4、2,能组成三角形,周长=4+4+2=10.
故答案为:10.
14.45°或36°
解:①如图1,
当过顶角的顶点的直线把它分成了两个等腰三角形,则AC=BC,AD=CD=BD,
设∠A=x°,
则∠ACD=∠A=x°,∠B=∠A=x°,
∴∠BCD=∠B=x°,
∵∠A+∠ACB+∠B=180°,
∴x+x+x+x=180,
解得x=45,
∴原等腰三角形的底角是45°;
②如图2,
△ABC中,AB=AC,BD=AD,AC=CD,
∵AB=AC,BD=AD,AC=CD,
∴∠B=∠C=∠BAD,∠CDA=∠CAD,
∵∠CDA=2∠B,
∴∠CAB=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°,
∴原等腰三角形的底角为36°;
故答案为45°或36°
15.false
解:设falsex°
∵false,
∴∠BAD=90°,
∴∠BAC=∠BAD+∠DAC=90°+ x°,
∵AB=AC,
∴∠B=∠C=false,
∵∠ADB为△ADC的外角,
∴∠ADB=∠DAC+∠C,即x°+false,
∴x=26.
故答案为26.
16.7
解:∵AB=9cm,
∴AC=AB=9cm,
∵DE是AB的垂直平分线,
∴AE=BE,
∴BE+CE=AE+CE=AC=AB=9cm,
∵△BCE的周长为16cm,
∴BC=16-9=7cm.
故答案为:7.
17.108
解:∵AB=AC,
∴∠B=∠C,
设∠B=∠C=x,
∵∠B=∠D,
∴∠D=x,
∵AE=ED,
∴∠EAD=∠D=x,
∵AE=AF,
∴∠AEF=∠AFE=90°-false,
∵∠AEF+∠AEB=180°,∠AFE+∠EFD=180°,
∴∠AEB=∠EFD=90°+false,
∵∠AEB=∠AED,
∴∠AED=90°+false,
∴∠FED=x,
在△EFD中,∠D+∠FED+∠EFD=180°,
∴x+90°+false+x=180°,
解得:x=36°,
∴∠BAC=180°-36°×2=108°,
故答案为:108.
18.50°或80°或20°
解:∵△PCD是等腰三角形,
∠PCD=120°-α,∠CPD=40°,
①当PC=PD时,
∴∠PCD=∠PDC=false=70°,即120°-α=70°,
∴∠α=50°;
②当PD=CD时,△PCD是等腰三角形,
∴∠PCD=∠CPD=40°,即120°-α=40°,
∴α=80°;
③当PC=CD时,△PCD是等腰三角形,
∴∠CDP=∠CPD=40°,
∴∠PCD=180°-2×40°=100°,
即120°-α=100°,
∴α=20°,
此时点P与点B重合,点D和A重合,
综合所述:当△PCD是等腰三角形时,α=50°或80°或20°.
故答案为:50°或80°或20°.
19.(1)△ABC的周长为10;(2)false.
解:(1)∵false,
∴a-2=0,b-4=0,
∴a=2,b=4,
∵△ABC为等腰三角形,
当2为腰时,则三边为2,2,4,
而2+2<4,不能组成三角形,舍去;
当2为底时,则三边为2,4,4,
而2+4>4,能组成三角形,
∴△ABC的周长为2+4+4=10;
(2)∵△ABC三条边的长分别为a、b、c,
∴false,false,false,
即false,false,
∴false
false
false
false.
20.见解析
解:证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵BE∥AD,
∴∠EBA=∠BAD,∠E=∠CAD,
∴∠EBA=∠E,
∴AE=AB,
又∵F是BE的中点,
∴AF⊥BE.
21.见解析.
解:∵false(已知),
∴false(等边对等角).
∵false(三角形的一个外角等于与它不相邻的两个内角的和),
false(已知),
∴false(等量代换).
∵false(已知),
∴false(等式性质).
在false与false中,
false,
∴false(ASA),
∴false(全等三角形的对应边相等).
22.(1)见解析;(2)20°
证明:∵DE⊥AC,∠B=90°,
∴∠B=∠AED=90°,
∵AC平分∠DAB,
∴∠BAC=∠EAD,
在△ABC和△AED中,
false,
∴△ABC≌△AED(ASA),
∴BC=DE;
(2)∵△ABC≌△AED,
∴AC=AD,
∴∠ACD=∠ADC,
∵∠DAC=40°,DE⊥AC,
∴∠ACD=∠ADC=70°,∠ADE=50°,
∴∠CDE=20°.
23.(1)见详解;(2)false
(1)证明:∵BD平分false,
∴false,
∵false,
∴false,
∴false,
∴false;
(2)解:∵false,
∴false,
由(1)可得false.
24.(1)false;(2)false;(3)不存在;答案见解析.
解:(1)由题意得BP=CQ=3t,
则CP=8﹣3t,
∵CP=CQ,
∴8﹣3t=3t,
解得,tfalse,
则当tfalse时,false;
(2)∵D为AB的中点,AB=AC=10,
∴BD=5,
∵△BPD≌△CQP,
∴BD=CP,
∴8﹣3t=5,
解得,t=1,
则当△BPD≌△CQP时,t=1;
(3)不存在,∵△BPD≌△CPQ,
∴BD=CQ,BP=CP,
则3t=5,3t=8﹣3t
解得,tfalse,tfalse,
∴不存在某一时刻t,使△BPD≌△CPQ.
一、单选题
1.如图,把一张长方形的纸,按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC是( )
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰直角三角形
2.若等腰三角形的周长为false,其中一边长为false,则该等腰三角形的底边为( )
A.false B.false C.false或false D.false
3.如图,AD=BC,AB=AC=BD,∠C=72°,则图中一共有( )个等腰三角形.
A.3 B.4 C.5 D.6
4.已知在平面直角坐标系false中,false点false在false轴或false轴上移动,若false三点可构成等腰三角形,则符合条件的false点有( )
A.false个 B.false个 C.false个 D.false个
5.如图,在false的正方形网格中有两个格点A、B,连接false,在网格中再找一个格点C,使得false是等腰直角三角形,满足条件的格点C的个数是( )
A.2 B.3 C.4 D.5
6.如图,在false中,false和false的角平分线交于点false,过点false作false交false于点false,交false于点false.若false,false,则false的长为( )
A.10 B.5.5 C.6 D.5
7.如图,在false中,false,以点false为圆心,任意长为半径画弧分别交false于点false和false,再分别以false为圆心,大于false的长为半径画弧,两弧交于点false,连接false并延长交false于点false,则下列结论不正确的是( )
A.false是∠BAC的平分线 B.false
C.点false在false的垂直平分线上 D.false
8.如图,已知OC平分∠AOB,false,若CD=3cm,则OD等于( )
A.3cm B.4cm C.1.5cm D.2cm
9.如图,△ABC中,∠B=2∠A,∠ACB的平分线CD交AB于点D,已知AC=16,BC=9,则BD的长为( )
A.6 B.7 C.8 D.9
10.在false中,false于D,false平分false交false于E,则下列结论一定成立的是( )
A.false B.false C.false D.false
11.如图,在false中,false,false,false的垂直平分线false交false于点false,交false于点false,若false,则false的长为( )
A.5 B.8 C.10 D.false
12.如图,在false中,false,false,false,则false的度数为( )
A.12° B.13° C.14° D.15°
二、填空题
13.若(a-4)2+|b-2|=0,则有两边长为a、b的等腰三角形的周长为________.
14.过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为____.
15.如图,在false中,false过点false作false,交false于点false,则false_______________________false.
16.如图,△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E,若AB=9cm,△BCE的周长为16cm,则BC=________cm.
17.如图,在false中,false,false是false边上一点,将false沿false翻折,点false落到点false的位置,false边与false边交于点false,如果false,那么false_________度.
18.在false中, false,将一块足够大的直角三角尺false按如图所示放置,顶点P在线段false上滑动,三角尺的直角边false始终经过点C,并且与false的夹角false,斜边false交false于点D.在点P的滑动过程中,若false是等腰三角形,则夹角false的大小是_____
三、解答题
19.已知,falseABC三条边的长分别为false.
(1)若false,当falseABC为等腰三角形,求falseABC的周长.
(2)化简:false.
20.如图,已知false平分false,false,false是false的中点,试说明false的理由,
21.如图,已知在等腰false中false,点D,点E和点F分别是false,false和false边上的点,且false,false,试说明false.
22.如图,在四边形ABCD中,∠B=90°,AC平分∠DAB,DE⊥AC,垂足为E,且AE=AB.
(1)求证:BC=DE;
(2)若∠DAC=40°,求∠CDE的度数.
23.如图,在false中,false的平分线交false于点false,过点false作false;交false于点false.
(1)求证:false;
(2)若false,求false的度数.
24.如图,在false中,false为false的中点,false,false,动点false从点false出发,沿false方向以3个单位长度每秒的速度向点false运动;同时动点false从点false出发,沿false方向以3个单位长度每秒的速度向点false运动,运动时间是false秒.
(1)在运动过程中,当false______秒时,false;
(2)在运动过程中,当false时,求出false的值;
(3)是否存在某一时刻false,使false?若存在,求出false的值;若不存在,请说明理由.
参考答案
1.C
解:由题可得,AB与AC可重合,即AB=AC,
∴△ABC是等腰三角形.
故选:C.
2.B
解:①4cm是底边时,腰长为false×(16-4)=6,能组成三角形,
②4cm是腰长时,底边为16-2×4=8,
∵4+4=8,
∴不能组成三角形,
综上所述,该等腰三角形的底边长为6cm.
故选:B.
3.C
解:∵AB=AC=BD,
∴△ABD与△BAC是等腰三角形,
在△ABD与△BAC中,
false,
∴△ABD≌△BAC(SSS),
∴∠D=∠C=72°,
∴∠BAD=∠D=∠C=∠ABC=72°,
∴∠∠ABD=∠BAC=36°,
∴∠DAE=∠CBE=36°,
∴∠AED=∠BEC=72°,
∴∠D=∠AED=∠C=∠BEC,
∴△ADE和△BCE是等腰三角形,
∵∠AED=∠BEC,
∴△ADE≌△BCE(AAS),
∴AE=BE,
∴△ABE是等腰三角形,
故选:C.
4.B
解:由题意得,false
①分别以点O和点A为圆心,5为半径作弧,交x轴和y轴,于点B1、B2、B5、B6、B7、B8,共6个点;
②AB的垂直平分线x轴和y轴,于点B3和B4,共两个点.
故答案为B.
5.B
解:如图:分情况讨论:
①AB为等腰直角△ABC底边时,符合条件的C点有0个;
②AB为等腰直角△ABC其中的一条腰时,符合条件的C点有3个.
故共有3个点,
故选:B.
6.D
解:∵MN∥BC,
∴∠MEB=∠CBE,∠NEC=∠BCE,
∵在△ABC中,∠ABC和∠ACB的平分线交于点E,
∴∠MBE=∠EBC,∠NCE=∠BCE,
∴∠MEB=∠MBE,∠NEC=∠NCE,
∴ME=MB,NE=NC,
∴MN=ME+NE=BM+CN=2+3=5,
故选:D.
7.D
解:根据作图方法可得false是false的平分线,故A正确;
∵false,
∴false.
∵false是false的平分线,
∴false.
∴false.故B正确;
过D作DE⊥AB
∵false,
∴false.
∴AE=BE
∴点D在false的垂直平分线上.故C正确;
∵false,
∴false,
∵false,
∴false.
∴false,false,
∴false,
∴false,
∴false,故D错误.
故选择:D.
8.A
解:false平分false,
false,
false,
false,
false,
false,
故选:A.
9.B
解:如图,在false上截取false 连接false
false平分false
false
false
false
false
false
false
false
false
false
false
false
false
故选:false
10.D
解:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠A=90°,
∴∠BCD=∠A.
∵CE平分∠ACD,
∴∠ACE=∠DCE.
又∵∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,
∴∠BEC=∠BCE,
∴BC=BE.
故选:D.
11.C
解:∵BC=AB,false,
∴∠C=∠A=36°,
∵false的垂直平分线false交false于点false,交false于点false,
∴AE=BE,
∴∠A=∠ABE=36°,
∴∠BEC=2∠A=72°,
∴∠CBE=180°-72°-36°=72°,
∴∠CBE=∠BEC,
∴CE=BC=AB=10,
故选:C.
12.D
解:如图,过C作CE⊥AD于E,过D作DF⊥BC于F.
∵∠CAD=30°,
∴∠ACE=60°,且CE=falseAC,
∵AC=AD,∠CAD=30°,
∴∠ACD=75°,
∴∠FCD=90°-∠ACD=15°,∠ECD=∠ACD-∠ACE=15°,
在△CED和△CFD中,
false,
∴△CED≌△CFD(AAS),
∴CF=CE=falseAC=falseBC,
∴CF=BF,
∵DF⊥BC,
∴BD=CD,
∴∠DCB=∠CBD=15°,
故选:D.
13.10
解:根据题意得,a-4=0,b-2=0,
解得a=4,b=2,
①若2是腰长,则底边为4,三角形的三边分别为2、2、4,不能组成三角形,
②若4是腰长,则底边为2,三角形的三边分别为4、4、2,能组成三角形,周长=4+4+2=10.
故答案为:10.
14.45°或36°
解:①如图1,
当过顶角的顶点的直线把它分成了两个等腰三角形,则AC=BC,AD=CD=BD,
设∠A=x°,
则∠ACD=∠A=x°,∠B=∠A=x°,
∴∠BCD=∠B=x°,
∵∠A+∠ACB+∠B=180°,
∴x+x+x+x=180,
解得x=45,
∴原等腰三角形的底角是45°;
②如图2,
△ABC中,AB=AC,BD=AD,AC=CD,
∵AB=AC,BD=AD,AC=CD,
∴∠B=∠C=∠BAD,∠CDA=∠CAD,
∵∠CDA=2∠B,
∴∠CAB=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°,
∴原等腰三角形的底角为36°;
故答案为45°或36°
15.false
解:设falsex°
∵false,
∴∠BAD=90°,
∴∠BAC=∠BAD+∠DAC=90°+ x°,
∵AB=AC,
∴∠B=∠C=false,
∵∠ADB为△ADC的外角,
∴∠ADB=∠DAC+∠C,即x°+false,
∴x=26.
故答案为26.
16.7
解:∵AB=9cm,
∴AC=AB=9cm,
∵DE是AB的垂直平分线,
∴AE=BE,
∴BE+CE=AE+CE=AC=AB=9cm,
∵△BCE的周长为16cm,
∴BC=16-9=7cm.
故答案为:7.
17.108
解:∵AB=AC,
∴∠B=∠C,
设∠B=∠C=x,
∵∠B=∠D,
∴∠D=x,
∵AE=ED,
∴∠EAD=∠D=x,
∵AE=AF,
∴∠AEF=∠AFE=90°-false,
∵∠AEF+∠AEB=180°,∠AFE+∠EFD=180°,
∴∠AEB=∠EFD=90°+false,
∵∠AEB=∠AED,
∴∠AED=90°+false,
∴∠FED=x,
在△EFD中,∠D+∠FED+∠EFD=180°,
∴x+90°+false+x=180°,
解得:x=36°,
∴∠BAC=180°-36°×2=108°,
故答案为:108.
18.50°或80°或20°
解:∵△PCD是等腰三角形,
∠PCD=120°-α,∠CPD=40°,
①当PC=PD时,
∴∠PCD=∠PDC=false=70°,即120°-α=70°,
∴∠α=50°;
②当PD=CD时,△PCD是等腰三角形,
∴∠PCD=∠CPD=40°,即120°-α=40°,
∴α=80°;
③当PC=CD时,△PCD是等腰三角形,
∴∠CDP=∠CPD=40°,
∴∠PCD=180°-2×40°=100°,
即120°-α=100°,
∴α=20°,
此时点P与点B重合,点D和A重合,
综合所述:当△PCD是等腰三角形时,α=50°或80°或20°.
故答案为:50°或80°或20°.
19.(1)△ABC的周长为10;(2)false.
解:(1)∵false,
∴a-2=0,b-4=0,
∴a=2,b=4,
∵△ABC为等腰三角形,
当2为腰时,则三边为2,2,4,
而2+2<4,不能组成三角形,舍去;
当2为底时,则三边为2,4,4,
而2+4>4,能组成三角形,
∴△ABC的周长为2+4+4=10;
(2)∵△ABC三条边的长分别为a、b、c,
∴false,false,false,
即false,false,
∴false
false
false
false.
20.见解析
解:证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵BE∥AD,
∴∠EBA=∠BAD,∠E=∠CAD,
∴∠EBA=∠E,
∴AE=AB,
又∵F是BE的中点,
∴AF⊥BE.
21.见解析.
解:∵false(已知),
∴false(等边对等角).
∵false(三角形的一个外角等于与它不相邻的两个内角的和),
false(已知),
∴false(等量代换).
∵false(已知),
∴false(等式性质).
在false与false中,
false,
∴false(ASA),
∴false(全等三角形的对应边相等).
22.(1)见解析;(2)20°
证明:∵DE⊥AC,∠B=90°,
∴∠B=∠AED=90°,
∵AC平分∠DAB,
∴∠BAC=∠EAD,
在△ABC和△AED中,
false,
∴△ABC≌△AED(ASA),
∴BC=DE;
(2)∵△ABC≌△AED,
∴AC=AD,
∴∠ACD=∠ADC,
∵∠DAC=40°,DE⊥AC,
∴∠ACD=∠ADC=70°,∠ADE=50°,
∴∠CDE=20°.
23.(1)见详解;(2)false
(1)证明:∵BD平分false,
∴false,
∵false,
∴false,
∴false,
∴false;
(2)解:∵false,
∴false,
由(1)可得false.
24.(1)false;(2)false;(3)不存在;答案见解析.
解:(1)由题意得BP=CQ=3t,
则CP=8﹣3t,
∵CP=CQ,
∴8﹣3t=3t,
解得,tfalse,
则当tfalse时,false;
(2)∵D为AB的中点,AB=AC=10,
∴BD=5,
∵△BPD≌△CQP,
∴BD=CP,
∴8﹣3t=5,
解得,t=1,
则当△BPD≌△CQP时,t=1;
(3)不存在,∵△BPD≌△CPQ,
∴BD=CQ,BP=CP,
则3t=5,3t=8﹣3t
解得,tfalse,tfalse,
∴不存在某一时刻t,使△BPD≌△CPQ.
