2021-2022学年人教版八年级数学上册14.2.1 平方差公式 同步练习 (word版含答案解析 )
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册14.2.1 平方差公式 同步练习 (word版含答案解析 ) |  | |
| 格式 | docx | ||
| 文件大小 | 305.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 17:21:42 | ||
图片预览



文档简介
14.2.1
平方差公式
一、单选题
1.下列式子中,能用平方差公式运算的是(
)
A.false
B.false
C.false
D.false
2.计算:false(
)
A.false
B.false
C.false
D.false
3.如图,在边长为false的正方形中央剪去一边长为(false)的小正方形(false),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为(
)
A.false
B.false
C.false
D.false
4.下列各式不能用平方差公式计算的是(
)
A.false
B.false
C.false
D.false
5.已知false,则false与false的大小是(
)
A.false
B.false
C.false
D.不能确定
6.定义false,例如false,则false的结果为(
)
A.false
B.false
C.false
D.false
7.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后得到的图形,小佳将阴影部分通过剪拼,拼成了图①、图②、图③三种新的图形,其中能够验证平方差公式的是( )
A.①②
B.①③
C.②③
D.①②③
8.若false,false,则false的值为(
)
A.false
B.false
C.false
D.2
9.如果用平方差公式计算false,则可将原式变形为(
)
A.false
B.false
C.false
D.false
10.一个自然数若能表示为相邻两个自然数的平方差,则这个自然数称为智数,比如:false,3就是智数,从0开始,不大于2021的智数共有(
)
A.false
B.false
C.false
D.以上都不对.
11.已知三个实数a、b、c满足a+b+c≠0,false,false,则(
)
A.a+b=c
B.ab=c
C.false
D.false
12.若2m﹣n=2,4m2﹣n2=12,则false的值为( )
A.﹣1
B.﹣3
C.﹣5
D.﹣9
二、填空题
13.false_______.
14.若a2﹣b2=6,b﹣a=false,则a+b的值为___.
15.把9991分解成两个自然数的积,这两个自然数是_________.
16.在一个边长为false的正方形中间挖出一个边长为false的正方形后,剩下的面积是__________.
17.点false与点false关于false轴对称,则false______.
18.我们学方差公式不但可以使运算简便,也可以解决一些复杂的数学问题.尝试计算(1+false)(1+false)(1+false)(1+false)+false的值是_______.
三、解答题
19.计算
(1)false
(2)20192﹣2017×2021
20.先化简,再求值:(x-3)(x+3)-(x2-2x+1),其中x=false.
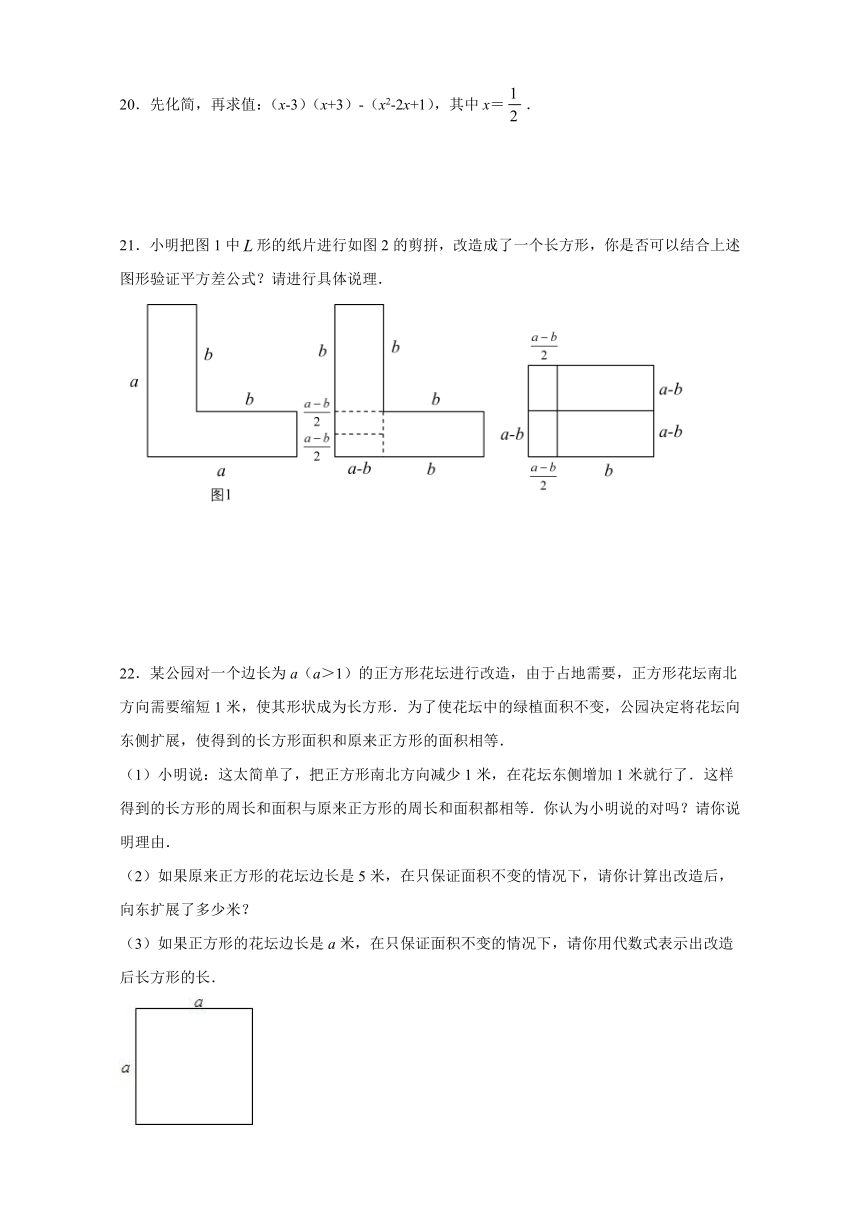
21.小明把图1中false形的纸片进行如图2的剪拼,改造成了一个长方形,你是否可以结合上述图形验证平方差公式?请进行具体说理.
22.某公园对一个边长为a(a>1)的正方形花坛进行改造,由于占地需要,正方形花坛南北方向需要缩短1米,使其形状成为长方形.为了使花坛中的绿植面积不变,公园决定将花坛向东侧扩展,使得到的长方形面积和原来正方形的面积相等.
(1)小明说:这太简单了,把正方形南北方向减少1米,在花坛东侧增加1米就行了.这样得到的长方形的周长和面积与原来正方形的周长和面积都相等.你认为小明说的对吗?请你说明理由.
(2)如果原来正方形的花坛边长是5米,在只保证面积不变的情况下,请你计算出改造后,向东扩展了多少米?
(3)如果正方形的花坛边长是a米,在只保证面积不变的情况下,请你用代数式表示出改造后长方形的长.
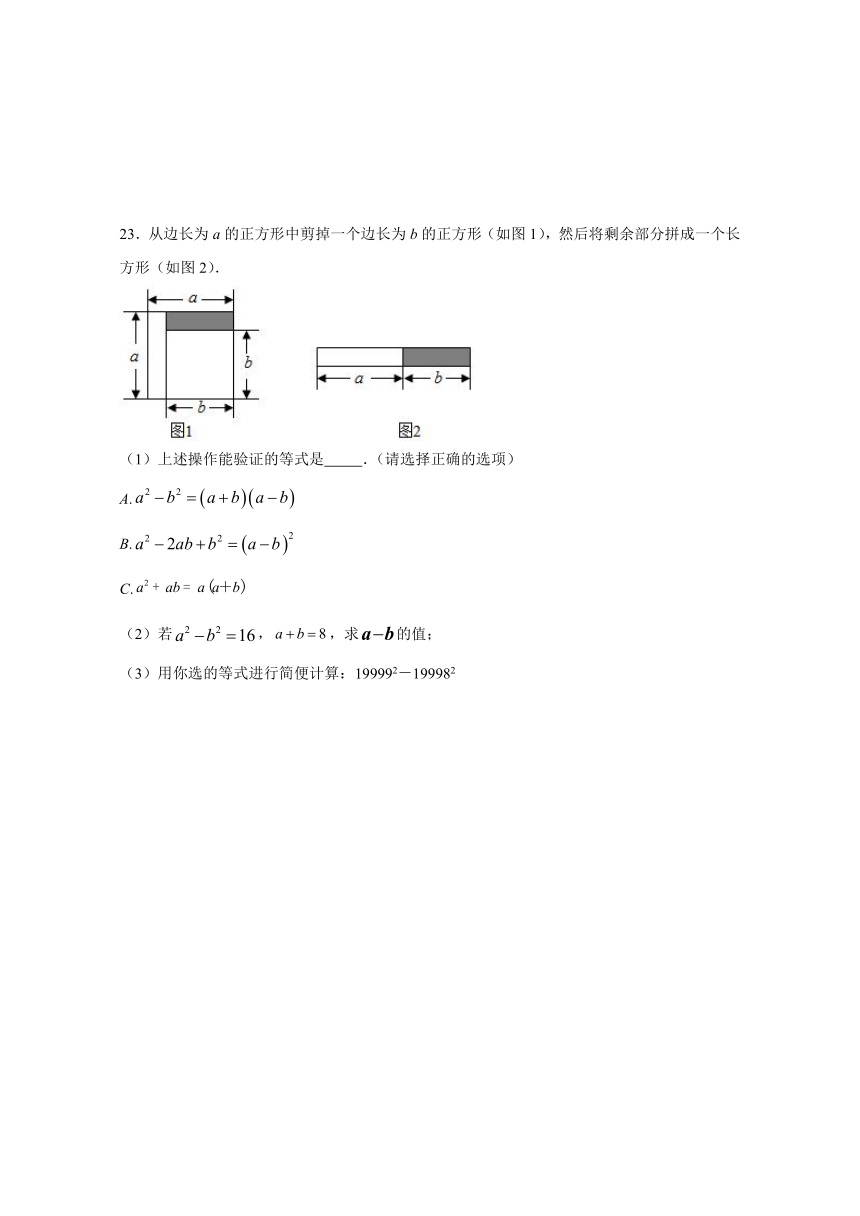
23.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是
.(请选择正确的选项)
A.false
B.false
C.false
(2)若false,false,求false的值;
(3)用你选的等式进行简便计算:199992-199982
参考答案
1.A
解:A选项,原式=x2falsey2,符合题意;
B选项,没有相反项,不符合题意;
C选项,没有相同项,不符合题意;
D选项,没有相同的项,不符合题意;
故选:A.
2.D
解:原式false.
故选:false.
3.C
解:(2a)2-(a+2)2
=4a2-a2-4a-4
=3a2-4a-4,
故选:C.
4.D
解:A、false,符合平方差公式的结构形式,能用平方差公式计算;
B、false,符合平方差公式的结构形式,能用平方差公式计算;
C、false,符合平方差公式的结构形式,能用平方差公式计算;
D、false,不符合平方差公式的结构形式,不能用平方差公式计算;
故选D.
5.A
解:false=false
=false
=false
=false
=1>0
∴M>N,
故选A.
6.B
解:根据题中的新定义得:
原式false.
故选:B.
7.D
解:(1)如图①,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的长为(a+b),宽为(a-b)的长方形,因此面积为(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以①符合题意;
(2)如图②,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的底为(a+b),高为(a-b)的平行四边形,因此面积为(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以②符合题意;
(3)如图③,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的上底为2b,下底为2a,,高为(a-b)的梯形,因此面积为false(2a+2b)(a-b)=(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以③符合题意;
综上所述,①②③都符合题意,
故选:D.
8.B
解:∵false,
∴false,
∴false.
故选:B.
9.C
解:false,
故选:false.
10.C
解:设相邻的两个自然数为为n,n+1,根据智数的定义,得 false,
∴2n+1≤2021,求n的整数解,即可.
∴2n≤2020,
∴n≤1010,
从0开始的,因此有1011个,
故选C.
11.D
解:∵a+c=false+false=a,
∴c=0,
∴false=0,
∴a-b+c=0,
∴a=b,
∴false=(a-b)(a+b)=0=c2.
故选:D.
12.A
解:∵4m2﹣n2=12,
∴(2m+n)(2m﹣n)=12,
∵2m﹣n=2,
∴2(2m+n)=12,
∴2m+n=6,
∴原式=false,
故选:A.
13.false
解:false
false
false
false.
故答案为:false.
14.-18
解:∵a2-b2=(a+b)(a-b)=6,b-a=false,
∴a-b=-(b-a)=false,
∴a+b=false.
故答案为:-18.
15.103,97
解:9991=10000-9=1002-32=(100+3)(100-3)=103×97,
故答案为:103,97.
16.130cm2
解:设剩下部分的面积为S,则
S=13.252-6.752=(13.25+6.75)×(13.25-6.75)=20×6.5=130cm2,
故答案为:130cm2.
17.false
解:false
点false与点false关于false轴对称,
false
false
false
故答案为:false
18.2
解:原式=false
=false
=false
……
=false
=false
=2.
故答案为:2.
19.(1)false;(2)4
解:(1)false
false
false;
(2)20192﹣2017×2021
false
false
false
false.
20.2x-10,-9
解:(x-3)(x+3)-(x2-2x+1)
=x2-9-x2+2x-1
=2x-10,
当x=false时,原式=2×false-10=1-10=-9.
21.可以,说理见解析
解:如图1,补全图形为正方形,
∴L型纸片的面积为:false;
如图3,图形面积为
false
=false
=false
∴可验证平方差公式:false.
22.(1)小明的说法不对,理由见解析;(2)向东扩展false米;(3)false
解:(1)小明的说法不对,理由如下:
由题意得:false,
∴小明的说法不对;
(2)设向东扩展x米,
由题意得false,
解得x=false,
答:向东扩展false米;
(3)改造后长方形的长为false
23.(1)A;(2)false;(3)false.
解:(1)图1得剩余部分的面积为:false,
图2把剩余部分拼成一个长方形,长为false,宽为false,面积为false,
∴false.
故选:A.
(2)∵false,
∴false,
∴false;
(3)199992-199982
false
false
false.
平方差公式
一、单选题
1.下列式子中,能用平方差公式运算的是(
)
A.false
B.false
C.false
D.false
2.计算:false(
)
A.false
B.false
C.false
D.false
3.如图,在边长为false的正方形中央剪去一边长为(false)的小正方形(false),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为(
)
A.false
B.false
C.false
D.false
4.下列各式不能用平方差公式计算的是(
)
A.false
B.false
C.false
D.false
5.已知false,则false与false的大小是(
)
A.false
B.false
C.false
D.不能确定
6.定义false,例如false,则false的结果为(
)
A.false
B.false
C.false
D.false
7.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后得到的图形,小佳将阴影部分通过剪拼,拼成了图①、图②、图③三种新的图形,其中能够验证平方差公式的是( )
A.①②
B.①③
C.②③
D.①②③
8.若false,false,则false的值为(
)
A.false
B.false
C.false
D.2
9.如果用平方差公式计算false,则可将原式变形为(
)
A.false
B.false
C.false
D.false
10.一个自然数若能表示为相邻两个自然数的平方差,则这个自然数称为智数,比如:false,3就是智数,从0开始,不大于2021的智数共有(
)
A.false
B.false
C.false
D.以上都不对.
11.已知三个实数a、b、c满足a+b+c≠0,false,false,则(
)
A.a+b=c
B.ab=c
C.false
D.false
12.若2m﹣n=2,4m2﹣n2=12,则false的值为( )
A.﹣1
B.﹣3
C.﹣5
D.﹣9
二、填空题
13.false_______.
14.若a2﹣b2=6,b﹣a=false,则a+b的值为___.
15.把9991分解成两个自然数的积,这两个自然数是_________.
16.在一个边长为false的正方形中间挖出一个边长为false的正方形后,剩下的面积是__________.
17.点false与点false关于false轴对称,则false______.
18.我们学方差公式不但可以使运算简便,也可以解决一些复杂的数学问题.尝试计算(1+false)(1+false)(1+false)(1+false)+false的值是_______.
三、解答题
19.计算
(1)false
(2)20192﹣2017×2021
20.先化简,再求值:(x-3)(x+3)-(x2-2x+1),其中x=false.
21.小明把图1中false形的纸片进行如图2的剪拼,改造成了一个长方形,你是否可以结合上述图形验证平方差公式?请进行具体说理.
22.某公园对一个边长为a(a>1)的正方形花坛进行改造,由于占地需要,正方形花坛南北方向需要缩短1米,使其形状成为长方形.为了使花坛中的绿植面积不变,公园决定将花坛向东侧扩展,使得到的长方形面积和原来正方形的面积相等.
(1)小明说:这太简单了,把正方形南北方向减少1米,在花坛东侧增加1米就行了.这样得到的长方形的周长和面积与原来正方形的周长和面积都相等.你认为小明说的对吗?请你说明理由.
(2)如果原来正方形的花坛边长是5米,在只保证面积不变的情况下,请你计算出改造后,向东扩展了多少米?
(3)如果正方形的花坛边长是a米,在只保证面积不变的情况下,请你用代数式表示出改造后长方形的长.
23.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是
.(请选择正确的选项)
A.false
B.false
C.false
(2)若false,false,求false的值;
(3)用你选的等式进行简便计算:199992-199982
参考答案
1.A
解:A选项,原式=x2falsey2,符合题意;
B选项,没有相反项,不符合题意;
C选项,没有相同项,不符合题意;
D选项,没有相同的项,不符合题意;
故选:A.
2.D
解:原式false.
故选:false.
3.C
解:(2a)2-(a+2)2
=4a2-a2-4a-4
=3a2-4a-4,
故选:C.
4.D
解:A、false,符合平方差公式的结构形式,能用平方差公式计算;
B、false,符合平方差公式的结构形式,能用平方差公式计算;
C、false,符合平方差公式的结构形式,能用平方差公式计算;
D、false,不符合平方差公式的结构形式,不能用平方差公式计算;
故选D.
5.A
解:false=false
=false
=false
=false
=1>0
∴M>N,
故选A.
6.B
解:根据题中的新定义得:
原式false.
故选:B.
7.D
解:(1)如图①,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的长为(a+b),宽为(a-b)的长方形,因此面积为(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以①符合题意;
(2)如图②,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的底为(a+b),高为(a-b)的平行四边形,因此面积为(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以②符合题意;
(3)如图③,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的上底为2b,下底为2a,,高为(a-b)的梯形,因此面积为false(2a+2b)(a-b)=(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以③符合题意;
综上所述,①②③都符合题意,
故选:D.
8.B
解:∵false,
∴false,
∴false.
故选:B.
9.C
解:false,
故选:false.
10.C
解:设相邻的两个自然数为为n,n+1,根据智数的定义,得 false,
∴2n+1≤2021,求n的整数解,即可.
∴2n≤2020,
∴n≤1010,
从0开始的,因此有1011个,
故选C.
11.D
解:∵a+c=false+false=a,
∴c=0,
∴false=0,
∴a-b+c=0,
∴a=b,
∴false=(a-b)(a+b)=0=c2.
故选:D.
12.A
解:∵4m2﹣n2=12,
∴(2m+n)(2m﹣n)=12,
∵2m﹣n=2,
∴2(2m+n)=12,
∴2m+n=6,
∴原式=false,
故选:A.
13.false
解:false
false
false
false.
故答案为:false.
14.-18
解:∵a2-b2=(a+b)(a-b)=6,b-a=false,
∴a-b=-(b-a)=false,
∴a+b=false.
故答案为:-18.
15.103,97
解:9991=10000-9=1002-32=(100+3)(100-3)=103×97,
故答案为:103,97.
16.130cm2
解:设剩下部分的面积为S,则
S=13.252-6.752=(13.25+6.75)×(13.25-6.75)=20×6.5=130cm2,
故答案为:130cm2.
17.false
解:false
点false与点false关于false轴对称,
false
false
false
故答案为:false
18.2
解:原式=false
=false
=false
……
=false
=false
=2.
故答案为:2.
19.(1)false;(2)4
解:(1)false
false
false;
(2)20192﹣2017×2021
false
false
false
false.
20.2x-10,-9
解:(x-3)(x+3)-(x2-2x+1)
=x2-9-x2+2x-1
=2x-10,
当x=false时,原式=2×false-10=1-10=-9.
21.可以,说理见解析
解:如图1,补全图形为正方形,
∴L型纸片的面积为:false;
如图3,图形面积为
false
=false
=false
∴可验证平方差公式:false.
22.(1)小明的说法不对,理由见解析;(2)向东扩展false米;(3)false
解:(1)小明的说法不对,理由如下:
由题意得:false,
∴小明的说法不对;
(2)设向东扩展x米,
由题意得false,
解得x=false,
答:向东扩展false米;
(3)改造后长方形的长为false
23.(1)A;(2)false;(3)false.
解:(1)图1得剩余部分的面积为:false,
图2把剩余部分拼成一个长方形,长为false,宽为false,面积为false,
∴false.
故选:A.
(2)∵false,
∴false,
∴false;
(3)199992-199982
false
false
false.
