2021-2022学年人教版八年级数学上册14.2.2 完全平方公式 同步练习 (word版含答案解析 )
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册14.2.2 完全平方公式 同步练习 (word版含答案解析 ) |

|
|
| 格式 | docx | ||
| 文件大小 | 392.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览



文档简介
14.2.2 完全平方公式
一、单选题
1.多项式false加上一个一次单项式后是一个完全平方式,这个单项式应为( )
A.false B.false C.false D.false
2.将false变形正确的是( )
A.false B.false
C.false D.false
3.如图,4张边长分别为false、false的长方形纸片围成一个正方形,从中可以得到的等式是( )
A.false B.false
C.false D.false
4.如果false是一个完全平方式,则false等于( )
A.false B.2 C.4 D.false
5.如图,两个正方形的边长分别为a和b,如果a+b=10,ab=22,那么阴影部分的面积是( )
A.15 B.17 C.20 D.22
6.若false,则false的值为( )
A.false B.2 C.3 D.4
7.利用乘法公式判断,下列等式何者成立?( )
A.false B.false
C.false D.false
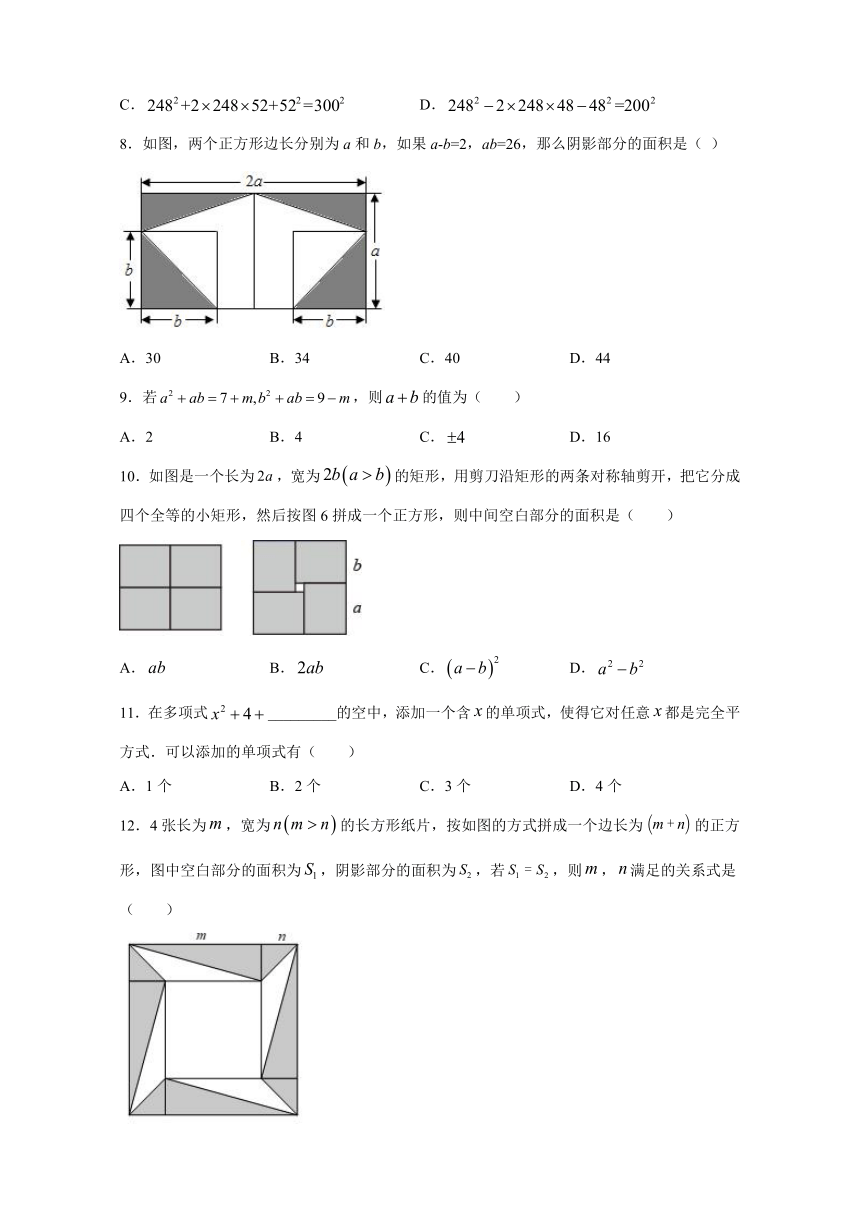
8.如图,两个正方形边长分别为a和b,如果a-b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
9.若false,则false的值为( )
A.2 B.4 C.false D.16
10.如图是一个长为false,宽为false的矩形,用剪刀沿矩形的两条对称轴剪开,把它分成四个全等的小矩形,然后按图6拼成一个正方形,则中间空白部分的面积是( )
A.false B.false C.false D.false
11.在多项式false_________的空中,添加一个含false的单项式,使得它对任意false都是完全平方式.可以添加的单项式有( )
A.1个 B.2个 C.3个 D.4个
12.4张长为false,宽为false的长方形纸片,按如图的方式拼成一个边长为false的正方形,图中空白部分的面积为false,阴影部分的面积为false,若false,则false,false满足的关系式是( )
A.false B.false C.false D.false
二、填空题
13.若false是完全平方式,则false
14.已知正方形的边长为false,如果它的边长增加6,那么它的面积增加___.
15.已知:false,则false的值为___.
16.公式(a-b)2=a2-2ab+b2可由公式(a+b)2=a2+2ab+b2推导得出,已知(a+b)3=a3+3a2b+3ab2+b3,则(a-b)3=______.
17.已知false的三边长false、false、false都是正整数,且满足false,则false的周长是________;
18.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为false;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为false.若false,则false+false= _______;当false+false=40时,则图3中阴影部分的面积false_________.
三、解答题
19.利用乘法公式计算:
(1)false (2)false
20.先化简再求值:false,其中false.
21.有些同学会想当然地认为false.
(1)举出反例说明该式不一定成立;
(2)计算false;
(3)直接写出当false、false满足什么条件,该式成立.
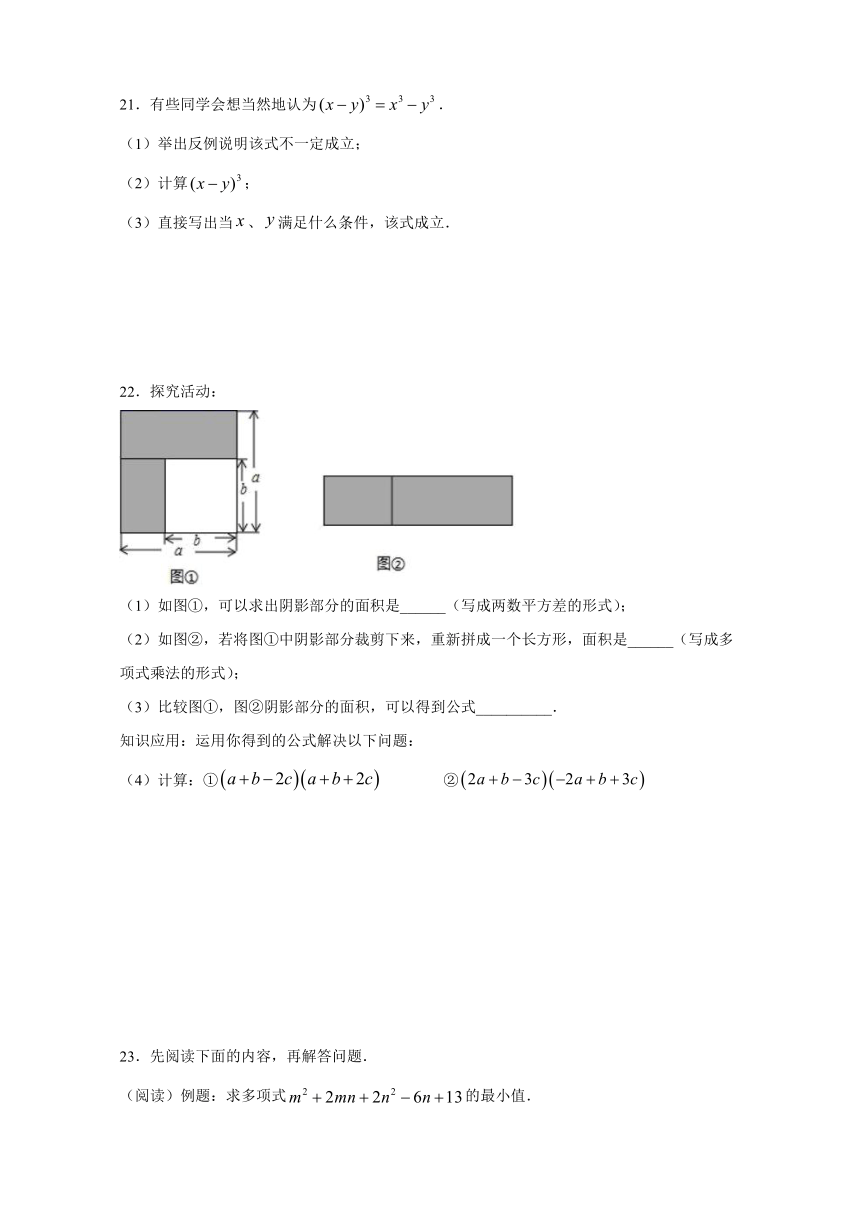
22.探究活动:
(1)如图①,可以求出阴影部分的面积是______(写成两数平方差的形式);
(2)如图②,若将图①中阴影部分裁剪下来,重新拼成一个长方形,面积是______(写成多项式乘法的形式);
(3)比较图①,图②阴影部分的面积,可以得到公式__________.
知识应用:运用你得到的公式解决以下问题:
(4)计算:①false ②false
23.先阅读下面的内容,再解答问题.
(阅读)例题:求多项式false的最小值.
解;false,
∵false
∴多项式false的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是____________;
(2)已知a、b、c是false的三边,且满足false,求第三边c的取值范围;
(3)求多项式false的最大值.
参考答案
1.D
解:多项式false加上一个一次单项式后是一个完全平方式,这个单项式可以为false.
故选:false.
2.C
解:false,
故选:C.
3.D
解:设大正方形的面积S1,小正方形的面积S2,
大正方形的边长为a+b,则大正方形面积S1=(a+b)2,
小正方形的边长为afalseb,则小正方形面积S2=(afalseb)2,
四个长方形的面积为4ab,
∵S1falseS2=4ab,
∴(a+b)2false(afalseb)2=4ab,
故选:D.
4.D
解:falsefalse是一个完全平方式,
false,
false,
即false,
故选:D.
5.B
解:由题意可得:阴影部分面积false.
false,false,
false,
false阴影部分面积false.
故选:B.
6.B
解:false,
false,
故选:B.
7.C
解: A、false不符合完全平方公式的特征且计算错误,完全平方公式的中间一项为false,所以不符合题意;
B、false不符合完全平方公式特征且计算错误,最后一项应为false,所以不符合题意;
C、false,所以符合题意;
D、false不符合完全平方公式特征且计算错误,最后一项应为false,所以不符合题意.
故选:C.
8.A
解:如图,
∵a-b=2,ab=26,
∴a2-2ab+b2=4,
∴a2+b2=4+2ab=4+52=56,
阴影部分的面积=S△ABC+S△CDM+S△AEF+S△GHM
=2×false(a-b)×a+2×falseb×b
=a(a-b)+b2
=a2+b2-ab
=56-26
=30.
故选:A.
9.C
解:∵a2+ab=7+m,b2+ab=9-m.
两式相加得:
∴a2+2ab+b2=16.
∴(a+b)2=16.
∴a+b=±4.
故选:C.
10.C
解:由题意可得,正方形的边长为false,
故正方形的面积为false,
又∵原矩形的面积为false,
∴中间空的部分的面积=false.
故选:C.
11.C
解:∵false,
∴可以添加含false的单项式为±4x;
∵false,
∴可以添加含false的单项式为false,
故选C.
12.D
解:由题意可得:S2=4×falsen(m+n)
=2n(m+n);
S1=(m+n)2-S2
=(m+n)2-(2mn+2n2)
=m2+2mn+n2-2mn-2n2
=m2-n2;
∵S1=S2,
∴2n(m+n)=m2-n2,
∴2n(m+n)=(m-n)(m+n),
∵m+n>0,
∴2n=m-n,
∴m=3n.
故选:D.
13.false
解:∵false是完全平方式,
∴false,
∴false,
故答案为:false12
14.false
解:根据题意,新正方形的边长为a+6,
∴增加的面积为false=false=false,
故答案为:false.
15.18
解:false,将等式false两边都除以false,得:
false
falsefalse
false
即:false
falsefalsefalse
故答案为:false
16.a3-3a2b+3ab2-b3
解:(a-b)3
=(a-b)2(a-b)
=(a2-2ab+b2)(a-b)
=a3-2a2b+ab2-a2b+2ab2-b3
=a3-3a2b+3ab2-b3,
故答案为:a3-3a2b+3ab2-b3.
17.7
解:falsefalse
false
false
false
false
false
falsefalse、false、false都是正整数
false
falsefalse的周长falsefalse
故答案为:7
18.34 20
解:①falsefalse,false
falsefalse+false=false
false
falsefalse
falsefalse+false=false
②false
false
falsefalse+false=false=40
false,
故答案为:34;20.
19.(1)false;(2)false.
解:(1)false,
false,
false,
false;
(2)false,
false,
false,
false,
false.
20.false,12
解:原式false,
当false时,原式false.
21.(1)见解析;(2)false;(3)false
解:(1)令false,false ,(反例不唯一)
∵ false,false, false,
∴该等式不一定成立;
(2)false false
=false
=false,
即false
(3)将false代入false中,
得: false,false,0=0,
∴当false、false满足x=y时,该式成立.
22.(1)false;(2)false;(3)false;(4)①false;②false
解:(1)阴影部分的面积是:a2-b2,
故答案是:a2-b2;
(2)长方形的面积是(a+b)(a-b),
故答案是:(a+b)(a-b);
(3)可以得到公式:a2-b2=(a+b)(a-b),
故答案是:a2-b2=(a+b)(a-b);
(4)计算:①false,
false,
false;
②false,
false,
false.
23.(1)完全平方公式;(2)1<c<9;(3)18
解:(1)例题解答过程中因式分解运用的公式是完全平方公式,
故答案为:完全平方公式;
(2)a2+b2=10a+8b-41,
a2-10a+25+b2-8b+16=0,
(a-5)2+(b-4)2=0.
∵(a-5)2≥0,(b-4)2≥0,
∴a-5=0,b-4=0,
∴a=5,b=4,
∴5-4<c<5+4,即1<c<9;
(3)原式=false
=false
=false
∵-2(x-y)2≤0,-(y+3)2≤0,
∴多项式false的最大值是18.
一、单选题
1.多项式false加上一个一次单项式后是一个完全平方式,这个单项式应为( )
A.false B.false C.false D.false
2.将false变形正确的是( )
A.false B.false
C.false D.false
3.如图,4张边长分别为false、false的长方形纸片围成一个正方形,从中可以得到的等式是( )
A.false B.false
C.false D.false
4.如果false是一个完全平方式,则false等于( )
A.false B.2 C.4 D.false
5.如图,两个正方形的边长分别为a和b,如果a+b=10,ab=22,那么阴影部分的面积是( )
A.15 B.17 C.20 D.22
6.若false,则false的值为( )
A.false B.2 C.3 D.4
7.利用乘法公式判断,下列等式何者成立?( )
A.false B.false
C.false D.false
8.如图,两个正方形边长分别为a和b,如果a-b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
9.若false,则false的值为( )
A.2 B.4 C.false D.16
10.如图是一个长为false,宽为false的矩形,用剪刀沿矩形的两条对称轴剪开,把它分成四个全等的小矩形,然后按图6拼成一个正方形,则中间空白部分的面积是( )
A.false B.false C.false D.false
11.在多项式false_________的空中,添加一个含false的单项式,使得它对任意false都是完全平方式.可以添加的单项式有( )
A.1个 B.2个 C.3个 D.4个
12.4张长为false,宽为false的长方形纸片,按如图的方式拼成一个边长为false的正方形,图中空白部分的面积为false,阴影部分的面积为false,若false,则false,false满足的关系式是( )
A.false B.false C.false D.false
二、填空题
13.若false是完全平方式,则false
14.已知正方形的边长为false,如果它的边长增加6,那么它的面积增加___.
15.已知:false,则false的值为___.
16.公式(a-b)2=a2-2ab+b2可由公式(a+b)2=a2+2ab+b2推导得出,已知(a+b)3=a3+3a2b+3ab2+b3,则(a-b)3=______.
17.已知false的三边长false、false、false都是正整数,且满足false,则false的周长是________;
18.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为false;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为false.若false,则false+false= _______;当false+false=40时,则图3中阴影部分的面积false_________.
三、解答题
19.利用乘法公式计算:
(1)false (2)false
20.先化简再求值:false,其中false.
21.有些同学会想当然地认为false.
(1)举出反例说明该式不一定成立;
(2)计算false;
(3)直接写出当false、false满足什么条件,该式成立.
22.探究活动:
(1)如图①,可以求出阴影部分的面积是______(写成两数平方差的形式);
(2)如图②,若将图①中阴影部分裁剪下来,重新拼成一个长方形,面积是______(写成多项式乘法的形式);
(3)比较图①,图②阴影部分的面积,可以得到公式__________.
知识应用:运用你得到的公式解决以下问题:
(4)计算:①false ②false
23.先阅读下面的内容,再解答问题.
(阅读)例题:求多项式false的最小值.
解;false,
∵false
∴多项式false的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是____________;
(2)已知a、b、c是false的三边,且满足false,求第三边c的取值范围;
(3)求多项式false的最大值.
参考答案
1.D
解:多项式false加上一个一次单项式后是一个完全平方式,这个单项式可以为false.
故选:false.
2.C
解:false,
故选:C.
3.D
解:设大正方形的面积S1,小正方形的面积S2,
大正方形的边长为a+b,则大正方形面积S1=(a+b)2,
小正方形的边长为afalseb,则小正方形面积S2=(afalseb)2,
四个长方形的面积为4ab,
∵S1falseS2=4ab,
∴(a+b)2false(afalseb)2=4ab,
故选:D.
4.D
解:falsefalse是一个完全平方式,
false,
false,
即false,
故选:D.
5.B
解:由题意可得:阴影部分面积false.
false,false,
false,
false阴影部分面积false.
故选:B.
6.B
解:false,
false,
故选:B.
7.C
解: A、false不符合完全平方公式的特征且计算错误,完全平方公式的中间一项为false,所以不符合题意;
B、false不符合完全平方公式特征且计算错误,最后一项应为false,所以不符合题意;
C、false,所以符合题意;
D、false不符合完全平方公式特征且计算错误,最后一项应为false,所以不符合题意.
故选:C.
8.A
解:如图,
∵a-b=2,ab=26,
∴a2-2ab+b2=4,
∴a2+b2=4+2ab=4+52=56,
阴影部分的面积=S△ABC+S△CDM+S△AEF+S△GHM
=2×false(a-b)×a+2×falseb×b
=a(a-b)+b2
=a2+b2-ab
=56-26
=30.
故选:A.
9.C
解:∵a2+ab=7+m,b2+ab=9-m.
两式相加得:
∴a2+2ab+b2=16.
∴(a+b)2=16.
∴a+b=±4.
故选:C.
10.C
解:由题意可得,正方形的边长为false,
故正方形的面积为false,
又∵原矩形的面积为false,
∴中间空的部分的面积=false.
故选:C.
11.C
解:∵false,
∴可以添加含false的单项式为±4x;
∵false,
∴可以添加含false的单项式为false,
故选C.
12.D
解:由题意可得:S2=4×falsen(m+n)
=2n(m+n);
S1=(m+n)2-S2
=(m+n)2-(2mn+2n2)
=m2+2mn+n2-2mn-2n2
=m2-n2;
∵S1=S2,
∴2n(m+n)=m2-n2,
∴2n(m+n)=(m-n)(m+n),
∵m+n>0,
∴2n=m-n,
∴m=3n.
故选:D.
13.false
解:∵false是完全平方式,
∴false,
∴false,
故答案为:false12
14.false
解:根据题意,新正方形的边长为a+6,
∴增加的面积为false=false=false,
故答案为:false.
15.18
解:false,将等式false两边都除以false,得:
false
falsefalse
false
即:false
falsefalsefalse
故答案为:false
16.a3-3a2b+3ab2-b3
解:(a-b)3
=(a-b)2(a-b)
=(a2-2ab+b2)(a-b)
=a3-2a2b+ab2-a2b+2ab2-b3
=a3-3a2b+3ab2-b3,
故答案为:a3-3a2b+3ab2-b3.
17.7
解:falsefalse
false
false
false
false
false
falsefalse、false、false都是正整数
false
falsefalse的周长falsefalse
故答案为:7
18.34 20
解:①falsefalse,false
falsefalse+false=false
false
falsefalse
falsefalse+false=false
②false
false
falsefalse+false=false=40
false,
故答案为:34;20.
19.(1)false;(2)false.
解:(1)false,
false,
false,
false;
(2)false,
false,
false,
false,
false.
20.false,12
解:原式false,
当false时,原式false.
21.(1)见解析;(2)false;(3)false
解:(1)令false,false ,(反例不唯一)
∵ false,false, false,
∴该等式不一定成立;
(2)false false
=false
=false,
即false
(3)将false代入false中,
得: false,false,0=0,
∴当false、false满足x=y时,该式成立.
22.(1)false;(2)false;(3)false;(4)①false;②false
解:(1)阴影部分的面积是:a2-b2,
故答案是:a2-b2;
(2)长方形的面积是(a+b)(a-b),
故答案是:(a+b)(a-b);
(3)可以得到公式:a2-b2=(a+b)(a-b),
故答案是:a2-b2=(a+b)(a-b);
(4)计算:①false,
false,
false;
②false,
false,
false.
23.(1)完全平方公式;(2)1<c<9;(3)18
解:(1)例题解答过程中因式分解运用的公式是完全平方公式,
故答案为:完全平方公式;
(2)a2+b2=10a+8b-41,
a2-10a+25+b2-8b+16=0,
(a-5)2+(b-4)2=0.
∵(a-5)2≥0,(b-4)2≥0,
∴a-5=0,b-4=0,
∴a=5,b=4,
∴5-4<c<5+4,即1<c<9;
(3)原式=false
=false
=false
∵-2(x-y)2≤0,-(y+3)2≤0,
∴多项式false的最大值是18.
