4.1.2点、线、体、面同步课时训练-2021-2022学年七年级数学人教版上册 (广东地区专用)(Word版 含答案)
文档属性
| 名称 | 4.1.2点、线、体、面同步课时训练-2021-2022学年七年级数学人教版上册 (广东地区专用)(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 343.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览




文档简介
1127760012331700同步课时训练-2021-2022学年七年级数学人教版上册 (广东地区)
4.1.2点、线、体、面
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共8个小题)
1.(2020·广东·七年级期末)如图,沿图中虚线旋转一周,形成的几何体是由( )个面围成的
A.1 B.2 C.3 D.4
1题图 2题图 4题图
2.如图所示的立体图形,是由__个面组成的,面与面相交形成___条线( )
A.3,6 B.4,5 C.4,6 D.5,7
3.电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于( )
A.点动成线 B.线动成面 C.面动成体 D.以上都不对
4.(2019·山西七年级期末)汽车的雨刷把玻璃上的雨雪刷干净属于以下哪项几何知识的实际应用( )
A.点动成线 B.线动成面
C.面动成体 D.以上答案都正确
5.(2021·内蒙古七年级期末)下列各选项中的图形能够绕虚线旋转一周得到如图所示几何体的是( )
A. B. C. D.
6.(2021·山东七年级期末)已知一个直角三角形的两条直角边长分别是:3cm和4cm,以其中一条直角边所在直线为轴旋转一周,得到的几何体的底面积是( )
A.false B.false
C.false或false D.false或false
7.(2020·广东深圳市·七年级期末)如图,用一个平面去截正方体截面形状不可能为下图中的( )
A. B. C. D.
8.(2020·河南郑州市·)一个物体的外形是长方体(如图(1)),其内部构造不祥.用平面横向自上而下截这个物体时,得到了一组截面,截面形状如图(2)所示,这个长方体的内部构造是( )
A.圆柱 B.球 C.圆锥 D.圆柱或球
二、填空题
9.(河北省唐山市路南区2020-2021学年七年级上学期期末考试数学试题(万唯))“天空中的流星”,用数学知识解释为:_____________.
10.(第28课时4.1.2点、线、面、体(基础练)-2020-2021学年七年级数学上册十分钟同步课堂专练(人教版))飞机表演“飞机拉线”时,我们用数学的知识可解释为点动成线.用数学知识解释下列现象:
(1)流星从空中划过留下的痕迹可解释为______;
(2)自行车的辐条运动可解释为_____;
(3)一只蚂蚁行走的路线可解释为_____;
(4)打开折扇得到扇面可解释为_____;
(5)一个圆面沿着它的一条直径旋转一周成球可解释为____.
11.(2020·渠县文崇中学七年级月考)一个棱柱的面数为14,棱数是36,则其顶点数为________.
12.如图,各图中的阴影部分绕着直线l旋转360°,所形成的立体图形依次是_______.
13.(2020·辽宁七年级期中)下面几何体截面图形的形状是长方形的是_____________.(只填序号)
14.(2021·山西晋中市·七年级期末)用一个平面去截一个几何体,截面形状为长方形,则这个几何体可能为:①正方体;②三棱锥;③圆柱;④圆锥 __________(写出所有正确结果的序号).
15.(2021·桥柱中学七年级期末)如图所示,截去正方体的一角变成一个多面体,这个多面体有____条棱,有____个顶点.
16.(2021年黑龙江省齐齐哈尔市铁锋区中考数学一模试卷)直角三角形的两条边的长分别是false和false,以直角边所在的直线为轴,将三角形旋转一周,所得几何体的底面积是________false.
三、解答题
17.(2017·广东河源市·正德中学七年级)用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.
A( );B( );C( );D( );E( ).
18.(2019·佛山市实验学校七年级月考)如图所示是一个正六棱柱的平面展开图.
(1)请根据图中所标的尺寸,计算这个几何体的侧面积;
(2)这个棱柱共有多少个顶点?有多少个面?有多少条棱?
(3)试用含有n的式子表示n棱柱的顶点数,面数与棱的条数.
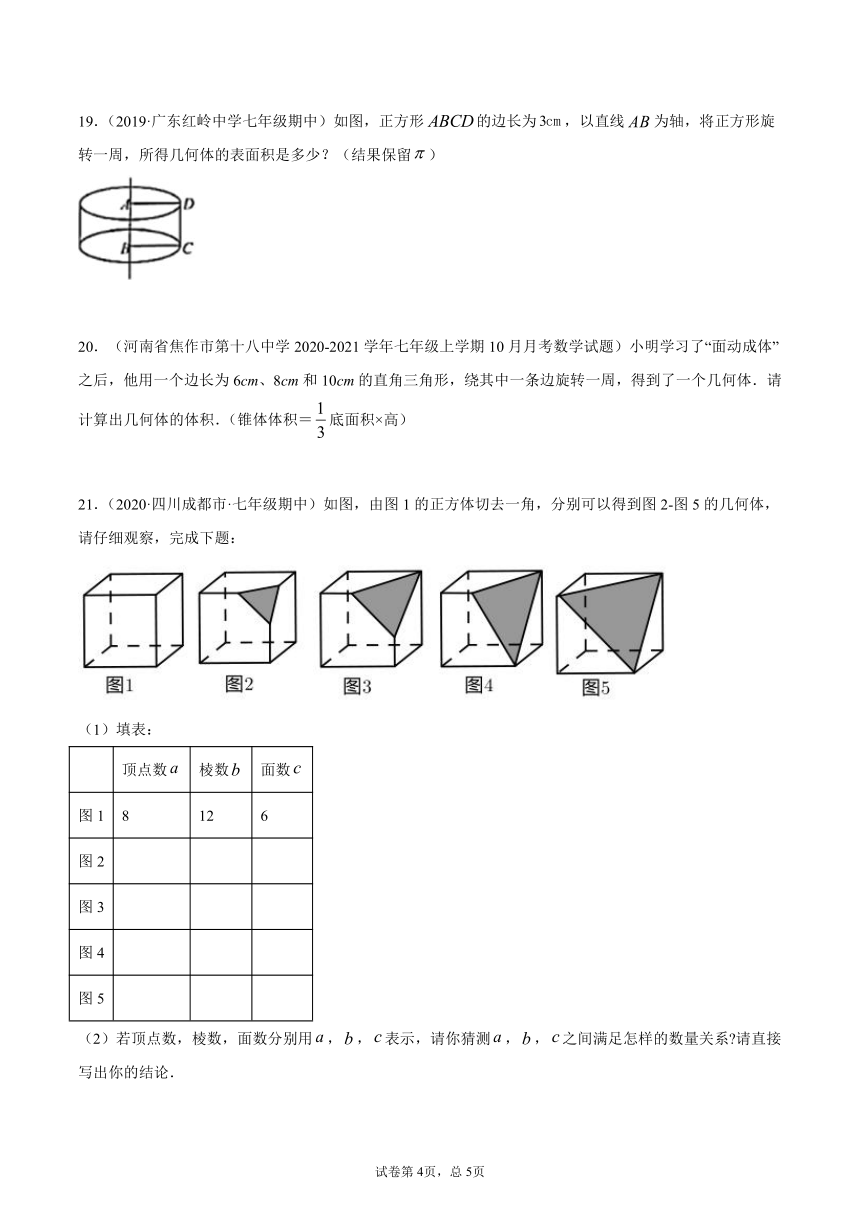
19.(2019·广东红岭中学七年级期中)如图,正方形false的边长为false,以直线false为轴,将正方形旋转一周,所得几何体的表面积是多少?(结果保留false)
(河南省焦作市第十八中学2020-2021学年七年级上学期10月月考数学试题)小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=false底面积×高)
21.(2020·四川成都市·七年级期中)如图,由图1的正方体切去一角,分别可以得到图2-图5的几何体,请仔细观察,完成下题:
(1)填表:
顶点数false
棱数false
面数false
图1
8
12
6
图2
图3
图4
图5
(2)若顶点数,棱数,面数分别用false,false,false表示,请你猜测false,false,false之间满足怎样的数量关系?请直接写出你的结论.
22.(2020·青岛市崂山区第四中学七年级月考)如图所示,已知直角三角形纸板ABC,直角边false,false.
false将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到______ 种大小不同的几何体?
false分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?false圆锥的体积false,其中false取false
参考答案
1.C
【思路点拨】根据直角梯形绕直角边旋转是圆台,可得答案.
【详细解答】解:直角梯形绕直角边旋转是圆台,由两个圆面一个曲面围成,共由三个面围成,
故C正确;
故选择:C.
【方法总结】本题考查点、线、面、体.解题的关键要理解直角梯形绕直角边旋转是圆台体.
2.C
【思路点拨】对图进行仔细观察认真分析即解.
【详细解答】解:有上下两个平面,侧面是一个平面,一个曲面,共有4个面;面与面相交的地方形成线.上面是一条曲线,一条直线,侧面是两条直线,下面是一条曲线一条直线,共有6条线.
故选:C.
【方法总结】本题考查的知识点为:面有平面与曲面之分,线也有直线和曲线之分.应考虑完全.
3.B
【思路点拨】根据“线动成面”的意义得出答案.
【详细解答】解:孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于线动成面,
故选:B.
【方法总结】本题考查点、线、面、体之间的关系,理解“点动成线、线动成面,面动成体”是解决问题的关键.
4.B
【思路点拨】汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
【详细解答】汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
故选:B.
【方法总结】本题考查了点、线、面、体,正确理解点线面体的概念是解题的关键.
5.B
【思路点拨】根据面动成体判断出各选项中旋转得到立体图形即可得解.
【详细解答】解:A.旋转一周为球体,故本选项错误;
B.旋转一周为圆柱体,故本选项正确;
C.旋转一周能够得到圆台,故本选项正确;
D.旋转一周能够得到圆锥,故本选项错误.
故选B.
【方法总结】本题考查了点、线、面、体,熟悉并判断出旋转后的立体图形是解题的关键.
6.D
【思路点拨】旋转后得到的几何体为圆锥,圆锥的底面为圆,半径为3cm或4cm,根据圆的面积计算即可.
【详细解答】解:由题意知,底面半径为3cm或4cm,
所以,底面面积为false或false,
故选D.
【方法总结】本题考查圆锥的底面积,利用了圆的面积公式S=R2,注意底面半径有两种情况.
7.A
【思路点拨】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此截面的形状可能是:三角形、四边形、五边形、六边形.
【详细解答】解:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为圆形.
故选:A.
【方法总结】本题考查正方体的截面.正方体的截面的四种情况应熟记.
8.C
【思路点拨】观察截面形状可发现,长方体内部的圆自上而下由大圆逐渐变成小圆、点,符合圆锥截面的性质.
【详细解答】解:观察截面形状可知,这个长方体的内部构造是长方体中间有一圆锥状空洞,
故选:C.
【方法总结】本题考查了截一个几何体,解答的关键是熟悉常见的几何体的截面,由截面的形状想象复杂几何体的组成.
9.点动成线
【思路点拨】流星是点,光线是线即可得出
【详细解答】∵流星是点,光线是线
∴点动成线
故答案为:点动成线
【方法总结】本题考查点与线之间的关系,正确理解点、线、面、体之间的关系是关键
10.点动成线 线动成面 点动成线 线动成面 面动成体
【思路点拨】根据从运动的观点来看点动成线,线动成面,面动成体填空即可.
【详细解答】(1)流星从空中划过留下的痕迹可解释为点动成线;
(2)自行车的辐条运动可解释为线动成面;
(3)一只蚂蚁行走的路线可解释为点动成线;
(4)打开折扇得到扇面可解释为线动成面;
(5)一个圆面沿着它的一条直径旋转一周成球可解释为面动成体.
故答案为:点动成线;线动成面;点动成线;线动成面;面动成体
【方法总结】此题主要考查了点、线、面、体,关键是掌握四者之间的关系.
11.24
【思路点拨】利用简单多面体的顶点数V,面数F及棱数E之间的关系为:V+F-E=2,这个公式叫做欧拉公式,公式描述了简单多面体顶点数、面数、棱数特有的规律,进而得出答案.
【详细解答】∵简单多面体的顶点数V,面数F及棱数E之间的关系为:V+F-E=2,
一个棱柱的面数为14,棱数为36,
∴ 顶点数为:V+14-36=2,
解得:V=24.
故答案为:24.
【方法总结】本题考查了欧拉公式,正确记忆公式是解题的关键;
12.圆柱、圆锥、球体(球)
【思路点拨】长方形旋转得圆柱,三角形旋转可得圆锥,半圆旋转得球即可.
【详细解答】解:根据各图中的阴影图形绕着直线I旋转360°,各能形成圆柱、圆锥、球.
故答案为:圆柱、圆锥、球.
【方法总结】本题考查的是面动成体的知识,掌握圆柱、圆锥与球都是旋转体,是由长方形,三角形半圆旋转一周的几何体.
13.(1)(4)
【思路点拨】根据立体几何的截面图形特征可直接进行求解.
【详细解答】解:由图及题意可得:
(1)是长方形,(2)是圆,(3)是梯形,(4)是长方形,(5)是平行四边形;
∴几何体截面图形的形状是长方形的是(1)(4);
故答案为(1)(4).
【方法总结】本题主要考查立体几何的截面图形,熟练掌握立体几何图形的结构特征是解题的关键.
14.①③
【思路点拨】估计正方体、三棱锥、圆柱、圆锥的几何体形状逐项分析解题.
【详细解答】解:①用一个平面去截正方体,截面形状可能是长方形,故①符合题意;
②用一个平面去截三棱锥,截面形状不可能是长方形,故②不符合题意;
③用一个平面去截圆柱,截面形状可能是长方形,故③符合题意;
④用一个平面去截圆锥,截面形状不可能是长方形,故④不符合题意,
故正确结果的序号为:①③,
故答案为:①③.
【方法总结】本题考查用一个平面去截一个简单几何体所得到的平面图形,是基础考点,难度较易,掌握相关知识是解题关键.
15.12 7
【思路点拨】截去正方体一角变成一个多面体,这个多面体多了一个面、棱不变,少了一个顶点.
【详细解答】仔细观察图形,正确地数出多面体的棱数及顶点数,它们分别是12,7,
故填:12,7.
【方法总结】本题结合截面考查多面体的相关知识.对于一个多面体:顶点数+面数?棱数=2.
16.false或false或false
【思路点拨】旋转后得到的几何体为圆锥,圆锥的底面为圆,半径为3或4或false,根据圆的面积计算即可.
【详细解答】解:∵直角三角形的两条边的长分别是false和false,
∴两直角边的长为3或4或false,
∴以其中一条直角边所在直线为轴旋转一周所得几何体为圆锥,底面是圆,底面的半径为3或4或false,所以,底面面积为false或false或false.
故答案为:false或false或false.
【方法总结】本题主要考查了面动成体,关键是掌握圆的面积公式S=πR2.注意底面半径有两种情况.
17.A(1、5、6);B(1、3、4);C(1、2、3、4);D(5);E(3、5、6) .
【解析】
试题分析:分别分析五种图形的所有的截面情况,即可写出答案.
试题解析:A圆锥,截面有可能是三角形,圆,椭圆(不完全),
B三棱锥,截面有可能是三角形,正方形,梯形,
C正方体,截面有可能是三角形,四边形(矩形,正方形,梯形),五边形,六边形,
D球体,截面只可能是圆,
E圆柱体,截面有可能是椭圆(不完全),圆,矩形,
因此答案为:A(1、5、6);B(1、3、4);C(1、2、3、4);D(5);E(3、5、6) .
【点睛】截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.空间想象力对于解答此类题目也是比较关键的.
18.(1)96;(2)六棱柱有12个顶点,8个面,18条棱;(3)n棱柱有2n个顶点,n+2个面,3n条棱.
【思路点拨】(1)由图可得侧面积等于六个矩形的面积.;
(2)计算六棱柱的顶点、面和棱的数目即可;
(3)根据六棱柱总结n棱柱的规律即可.
【详细解答】解:(1)该棱柱的侧面积为:2×8×6=96;
(2)六棱柱有12个顶点,8个面,18条棱;
(3)n棱柱有2n个顶点,n+2个面,3n条棱;
【方法总结】本题考查了立体图形的侧面积、顶点、面和棱,解题的关键在于学生良好的空间思维能力.
19.所得几何体的表面积为false.
【思路点拨】根据正方形旋转一周后形成的几何体是圆柱体即可求得几何体的表面积.
【详细解答】直线false为轴,将正方形旋转一周可得圆柱体,圆柱的高为false,底面直径为false,
false所得几何体的表面积false
false
false
false.
答:所得几何体的表面积是false.
【方法总结】本题考查了作图-旋转变换、点、线、面、体以及几何体的表面积,解决本题的关键是理解正方形旋转一周后形成的几何体是圆柱体.
20.几何体的体积为:96πcm3或128πcm3或76.8πcm3.
【思路点拨】根据三角形旋转是圆锥,可得几何体;根据圆锥的体积公式,分类讨论可得答案.
【详细解答】解:以8cm为轴,得:
以8cm为轴体积为false×π×62×8=96π(cm3);
以6cm为轴,得:
以6cm为轴的体积为false×π×82×6=128π(cm3);
以10cm为轴,得
以10cm为轴的体积为false×π(false)2×10=76.8π(cm3).
故几何体的体积为:96πcm3或128πcm3或76.8πcm3.
【方法总结】本题考查了点线面体,利用三角形旋转是圆锥是解题关键.
21.(1)见解析;(2)false.
【思路点拨】(1)根据正方体原有的面数,顶点数,棱的条数,以及正方体截去一个角后,面、顶点、棱的变化情况,形数结合求解;
(2)利用以上所求得出false,false,false之间应满足的关系.
【详细解答】(1)表格如下所示:
顶点数false
棱数false
面数false
图1
8
12
6
图2
10
15
7
图3
9
14
7
图4
8
13
7
图5
7
12
7
(2)由(1)可知:
图1:false,
图2:false,
图3:false,
图4:false,
图5:false,
由此可得:false.
【方法总结】本题考查了正方体的截面.关键是明确正方体的面数,顶点数,棱的条数,形数结合,求出截去一个角后得到的几何体的面数,顶点数,棱的条数.
22.(1)3;(2)以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
【思路点拨】false将直角三角形纸板ABC绕三角形的三条边所在的直线分别旋转一周即可.
false如果以AB所在的直线旋转一周得到的圆锥的底面半径是8厘米,高是4厘米;如果以BC所在的直线旋转一周得到的圆锥的底面半径是4厘米,高是8厘米,根据圆锥的体积公式:false,把数据代入公式解答.
【详细解答】(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体,
故答案为:3
false以AB为轴:
false立方厘米false;
以BC为轴:
false立方厘米false.
答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
【方法总结】此题考查了点、线、面、体,关键是理解掌握圆锥的特征,以及圆锥体积公式的灵活运用.
4.1.2点、线、体、面
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共8个小题)
1.(2020·广东·七年级期末)如图,沿图中虚线旋转一周,形成的几何体是由( )个面围成的
A.1 B.2 C.3 D.4
1题图 2题图 4题图
2.如图所示的立体图形,是由__个面组成的,面与面相交形成___条线( )
A.3,6 B.4,5 C.4,6 D.5,7
3.电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于( )
A.点动成线 B.线动成面 C.面动成体 D.以上都不对
4.(2019·山西七年级期末)汽车的雨刷把玻璃上的雨雪刷干净属于以下哪项几何知识的实际应用( )
A.点动成线 B.线动成面
C.面动成体 D.以上答案都正确
5.(2021·内蒙古七年级期末)下列各选项中的图形能够绕虚线旋转一周得到如图所示几何体的是( )
A. B. C. D.
6.(2021·山东七年级期末)已知一个直角三角形的两条直角边长分别是:3cm和4cm,以其中一条直角边所在直线为轴旋转一周,得到的几何体的底面积是( )
A.false B.false
C.false或false D.false或false
7.(2020·广东深圳市·七年级期末)如图,用一个平面去截正方体截面形状不可能为下图中的( )
A. B. C. D.
8.(2020·河南郑州市·)一个物体的外形是长方体(如图(1)),其内部构造不祥.用平面横向自上而下截这个物体时,得到了一组截面,截面形状如图(2)所示,这个长方体的内部构造是( )
A.圆柱 B.球 C.圆锥 D.圆柱或球
二、填空题
9.(河北省唐山市路南区2020-2021学年七年级上学期期末考试数学试题(万唯))“天空中的流星”,用数学知识解释为:_____________.
10.(第28课时4.1.2点、线、面、体(基础练)-2020-2021学年七年级数学上册十分钟同步课堂专练(人教版))飞机表演“飞机拉线”时,我们用数学的知识可解释为点动成线.用数学知识解释下列现象:
(1)流星从空中划过留下的痕迹可解释为______;
(2)自行车的辐条运动可解释为_____;
(3)一只蚂蚁行走的路线可解释为_____;
(4)打开折扇得到扇面可解释为_____;
(5)一个圆面沿着它的一条直径旋转一周成球可解释为____.
11.(2020·渠县文崇中学七年级月考)一个棱柱的面数为14,棱数是36,则其顶点数为________.
12.如图,各图中的阴影部分绕着直线l旋转360°,所形成的立体图形依次是_______.
13.(2020·辽宁七年级期中)下面几何体截面图形的形状是长方形的是_____________.(只填序号)
14.(2021·山西晋中市·七年级期末)用一个平面去截一个几何体,截面形状为长方形,则这个几何体可能为:①正方体;②三棱锥;③圆柱;④圆锥 __________(写出所有正确结果的序号).
15.(2021·桥柱中学七年级期末)如图所示,截去正方体的一角变成一个多面体,这个多面体有____条棱,有____个顶点.
16.(2021年黑龙江省齐齐哈尔市铁锋区中考数学一模试卷)直角三角形的两条边的长分别是false和false,以直角边所在的直线为轴,将三角形旋转一周,所得几何体的底面积是________false.
三、解答题
17.(2017·广东河源市·正德中学七年级)用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.
A( );B( );C( );D( );E( ).
18.(2019·佛山市实验学校七年级月考)如图所示是一个正六棱柱的平面展开图.
(1)请根据图中所标的尺寸,计算这个几何体的侧面积;
(2)这个棱柱共有多少个顶点?有多少个面?有多少条棱?
(3)试用含有n的式子表示n棱柱的顶点数,面数与棱的条数.
19.(2019·广东红岭中学七年级期中)如图,正方形false的边长为false,以直线false为轴,将正方形旋转一周,所得几何体的表面积是多少?(结果保留false)
(河南省焦作市第十八中学2020-2021学年七年级上学期10月月考数学试题)小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=false底面积×高)
21.(2020·四川成都市·七年级期中)如图,由图1的正方体切去一角,分别可以得到图2-图5的几何体,请仔细观察,完成下题:
(1)填表:
顶点数false
棱数false
面数false
图1
8
12
6
图2
图3
图4
图5
(2)若顶点数,棱数,面数分别用false,false,false表示,请你猜测false,false,false之间满足怎样的数量关系?请直接写出你的结论.
22.(2020·青岛市崂山区第四中学七年级月考)如图所示,已知直角三角形纸板ABC,直角边false,false.
false将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到______ 种大小不同的几何体?
false分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?false圆锥的体积false,其中false取false
参考答案
1.C
【思路点拨】根据直角梯形绕直角边旋转是圆台,可得答案.
【详细解答】解:直角梯形绕直角边旋转是圆台,由两个圆面一个曲面围成,共由三个面围成,
故C正确;
故选择:C.
【方法总结】本题考查点、线、面、体.解题的关键要理解直角梯形绕直角边旋转是圆台体.
2.C
【思路点拨】对图进行仔细观察认真分析即解.
【详细解答】解:有上下两个平面,侧面是一个平面,一个曲面,共有4个面;面与面相交的地方形成线.上面是一条曲线,一条直线,侧面是两条直线,下面是一条曲线一条直线,共有6条线.
故选:C.
【方法总结】本题考查的知识点为:面有平面与曲面之分,线也有直线和曲线之分.应考虑完全.
3.B
【思路点拨】根据“线动成面”的意义得出答案.
【详细解答】解:孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于线动成面,
故选:B.
【方法总结】本题考查点、线、面、体之间的关系,理解“点动成线、线动成面,面动成体”是解决问题的关键.
4.B
【思路点拨】汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
【详细解答】汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
故选:B.
【方法总结】本题考查了点、线、面、体,正确理解点线面体的概念是解题的关键.
5.B
【思路点拨】根据面动成体判断出各选项中旋转得到立体图形即可得解.
【详细解答】解:A.旋转一周为球体,故本选项错误;
B.旋转一周为圆柱体,故本选项正确;
C.旋转一周能够得到圆台,故本选项正确;
D.旋转一周能够得到圆锥,故本选项错误.
故选B.
【方法总结】本题考查了点、线、面、体,熟悉并判断出旋转后的立体图形是解题的关键.
6.D
【思路点拨】旋转后得到的几何体为圆锥,圆锥的底面为圆,半径为3cm或4cm,根据圆的面积计算即可.
【详细解答】解:由题意知,底面半径为3cm或4cm,
所以,底面面积为false或false,
故选D.
【方法总结】本题考查圆锥的底面积,利用了圆的面积公式S=R2,注意底面半径有两种情况.
7.A
【思路点拨】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此截面的形状可能是:三角形、四边形、五边形、六边形.
【详细解答】解:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为圆形.
故选:A.
【方法总结】本题考查正方体的截面.正方体的截面的四种情况应熟记.
8.C
【思路点拨】观察截面形状可发现,长方体内部的圆自上而下由大圆逐渐变成小圆、点,符合圆锥截面的性质.
【详细解答】解:观察截面形状可知,这个长方体的内部构造是长方体中间有一圆锥状空洞,
故选:C.
【方法总结】本题考查了截一个几何体,解答的关键是熟悉常见的几何体的截面,由截面的形状想象复杂几何体的组成.
9.点动成线
【思路点拨】流星是点,光线是线即可得出
【详细解答】∵流星是点,光线是线
∴点动成线
故答案为:点动成线
【方法总结】本题考查点与线之间的关系,正确理解点、线、面、体之间的关系是关键
10.点动成线 线动成面 点动成线 线动成面 面动成体
【思路点拨】根据从运动的观点来看点动成线,线动成面,面动成体填空即可.
【详细解答】(1)流星从空中划过留下的痕迹可解释为点动成线;
(2)自行车的辐条运动可解释为线动成面;
(3)一只蚂蚁行走的路线可解释为点动成线;
(4)打开折扇得到扇面可解释为线动成面;
(5)一个圆面沿着它的一条直径旋转一周成球可解释为面动成体.
故答案为:点动成线;线动成面;点动成线;线动成面;面动成体
【方法总结】此题主要考查了点、线、面、体,关键是掌握四者之间的关系.
11.24
【思路点拨】利用简单多面体的顶点数V,面数F及棱数E之间的关系为:V+F-E=2,这个公式叫做欧拉公式,公式描述了简单多面体顶点数、面数、棱数特有的规律,进而得出答案.
【详细解答】∵简单多面体的顶点数V,面数F及棱数E之间的关系为:V+F-E=2,
一个棱柱的面数为14,棱数为36,
∴ 顶点数为:V+14-36=2,
解得:V=24.
故答案为:24.
【方法总结】本题考查了欧拉公式,正确记忆公式是解题的关键;
12.圆柱、圆锥、球体(球)
【思路点拨】长方形旋转得圆柱,三角形旋转可得圆锥,半圆旋转得球即可.
【详细解答】解:根据各图中的阴影图形绕着直线I旋转360°,各能形成圆柱、圆锥、球.
故答案为:圆柱、圆锥、球.
【方法总结】本题考查的是面动成体的知识,掌握圆柱、圆锥与球都是旋转体,是由长方形,三角形半圆旋转一周的几何体.
13.(1)(4)
【思路点拨】根据立体几何的截面图形特征可直接进行求解.
【详细解答】解:由图及题意可得:
(1)是长方形,(2)是圆,(3)是梯形,(4)是长方形,(5)是平行四边形;
∴几何体截面图形的形状是长方形的是(1)(4);
故答案为(1)(4).
【方法总结】本题主要考查立体几何的截面图形,熟练掌握立体几何图形的结构特征是解题的关键.
14.①③
【思路点拨】估计正方体、三棱锥、圆柱、圆锥的几何体形状逐项分析解题.
【详细解答】解:①用一个平面去截正方体,截面形状可能是长方形,故①符合题意;
②用一个平面去截三棱锥,截面形状不可能是长方形,故②不符合题意;
③用一个平面去截圆柱,截面形状可能是长方形,故③符合题意;
④用一个平面去截圆锥,截面形状不可能是长方形,故④不符合题意,
故正确结果的序号为:①③,
故答案为:①③.
【方法总结】本题考查用一个平面去截一个简单几何体所得到的平面图形,是基础考点,难度较易,掌握相关知识是解题关键.
15.12 7
【思路点拨】截去正方体一角变成一个多面体,这个多面体多了一个面、棱不变,少了一个顶点.
【详细解答】仔细观察图形,正确地数出多面体的棱数及顶点数,它们分别是12,7,
故填:12,7.
【方法总结】本题结合截面考查多面体的相关知识.对于一个多面体:顶点数+面数?棱数=2.
16.false或false或false
【思路点拨】旋转后得到的几何体为圆锥,圆锥的底面为圆,半径为3或4或false,根据圆的面积计算即可.
【详细解答】解:∵直角三角形的两条边的长分别是false和false,
∴两直角边的长为3或4或false,
∴以其中一条直角边所在直线为轴旋转一周所得几何体为圆锥,底面是圆,底面的半径为3或4或false,所以,底面面积为false或false或false.
故答案为:false或false或false.
【方法总结】本题主要考查了面动成体,关键是掌握圆的面积公式S=πR2.注意底面半径有两种情况.
17.A(1、5、6);B(1、3、4);C(1、2、3、4);D(5);E(3、5、6) .
【解析】
试题分析:分别分析五种图形的所有的截面情况,即可写出答案.
试题解析:A圆锥,截面有可能是三角形,圆,椭圆(不完全),
B三棱锥,截面有可能是三角形,正方形,梯形,
C正方体,截面有可能是三角形,四边形(矩形,正方形,梯形),五边形,六边形,
D球体,截面只可能是圆,
E圆柱体,截面有可能是椭圆(不完全),圆,矩形,
因此答案为:A(1、5、6);B(1、3、4);C(1、2、3、4);D(5);E(3、5、6) .
【点睛】截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.空间想象力对于解答此类题目也是比较关键的.
18.(1)96;(2)六棱柱有12个顶点,8个面,18条棱;(3)n棱柱有2n个顶点,n+2个面,3n条棱.
【思路点拨】(1)由图可得侧面积等于六个矩形的面积.;
(2)计算六棱柱的顶点、面和棱的数目即可;
(3)根据六棱柱总结n棱柱的规律即可.
【详细解答】解:(1)该棱柱的侧面积为:2×8×6=96;
(2)六棱柱有12个顶点,8个面,18条棱;
(3)n棱柱有2n个顶点,n+2个面,3n条棱;
【方法总结】本题考查了立体图形的侧面积、顶点、面和棱,解题的关键在于学生良好的空间思维能力.
19.所得几何体的表面积为false.
【思路点拨】根据正方形旋转一周后形成的几何体是圆柱体即可求得几何体的表面积.
【详细解答】直线false为轴,将正方形旋转一周可得圆柱体,圆柱的高为false,底面直径为false,
false所得几何体的表面积false
false
false
false.
答:所得几何体的表面积是false.
【方法总结】本题考查了作图-旋转变换、点、线、面、体以及几何体的表面积,解决本题的关键是理解正方形旋转一周后形成的几何体是圆柱体.
20.几何体的体积为:96πcm3或128πcm3或76.8πcm3.
【思路点拨】根据三角形旋转是圆锥,可得几何体;根据圆锥的体积公式,分类讨论可得答案.
【详细解答】解:以8cm为轴,得:
以8cm为轴体积为false×π×62×8=96π(cm3);
以6cm为轴,得:
以6cm为轴的体积为false×π×82×6=128π(cm3);
以10cm为轴,得
以10cm为轴的体积为false×π(false)2×10=76.8π(cm3).
故几何体的体积为:96πcm3或128πcm3或76.8πcm3.
【方法总结】本题考查了点线面体,利用三角形旋转是圆锥是解题关键.
21.(1)见解析;(2)false.
【思路点拨】(1)根据正方体原有的面数,顶点数,棱的条数,以及正方体截去一个角后,面、顶点、棱的变化情况,形数结合求解;
(2)利用以上所求得出false,false,false之间应满足的关系.
【详细解答】(1)表格如下所示:
顶点数false
棱数false
面数false
图1
8
12
6
图2
10
15
7
图3
9
14
7
图4
8
13
7
图5
7
12
7
(2)由(1)可知:
图1:false,
图2:false,
图3:false,
图4:false,
图5:false,
由此可得:false.
【方法总结】本题考查了正方体的截面.关键是明确正方体的面数,顶点数,棱的条数,形数结合,求出截去一个角后得到的几何体的面数,顶点数,棱的条数.
22.(1)3;(2)以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
【思路点拨】false将直角三角形纸板ABC绕三角形的三条边所在的直线分别旋转一周即可.
false如果以AB所在的直线旋转一周得到的圆锥的底面半径是8厘米,高是4厘米;如果以BC所在的直线旋转一周得到的圆锥的底面半径是4厘米,高是8厘米,根据圆锥的体积公式:false,把数据代入公式解答.
【详细解答】(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体,
故答案为:3
false以AB为轴:
false立方厘米false;
以BC为轴:
false立方厘米false.
答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
【方法总结】此题考查了点、线、面、体,关键是理解掌握圆锥的特征,以及圆锥体积公式的灵活运用.
