8.1正弦定理第一课时课件(共54张PPT)-湘教版数学必修4
文档属性
| 名称 | 8.1正弦定理第一课时课件(共54张PPT)-湘教版数学必修4 |

|
|
| 格式 | ppt | ||
| 文件大小 | 395.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览










文档简介
正弦定理
二、解三角形
1.解三角形时常用的结论
(1)在△ABC中,A>B?⑤________?⑥________;(即在一个三角形中大边对大角)
(2)a+b>c,b+c>a,⑦________;(即在一个三角形中两边之和大于第三边,两边之差小于第三边)
(3)内角和定理:△ABC中,A+B+C=⑧________.
2.正弦定理的应用
利用正弦定理可以解决以下两类有关三角形的问题:
(1)已知两角和任意一边,求其他⑨________和⑩________;
(2)已知两边和其中一边的对角,求?________,从而进一步求出其他的边和角.
对于第(1)类,其解是唯一确定的,一般先由三角形内角和为180°求得?________,再利用正弦定理求其余两边;
对于第(2)类,其解不一定唯一,由于三角形的形状不能唯一确定,因而会出现?________三种情况.
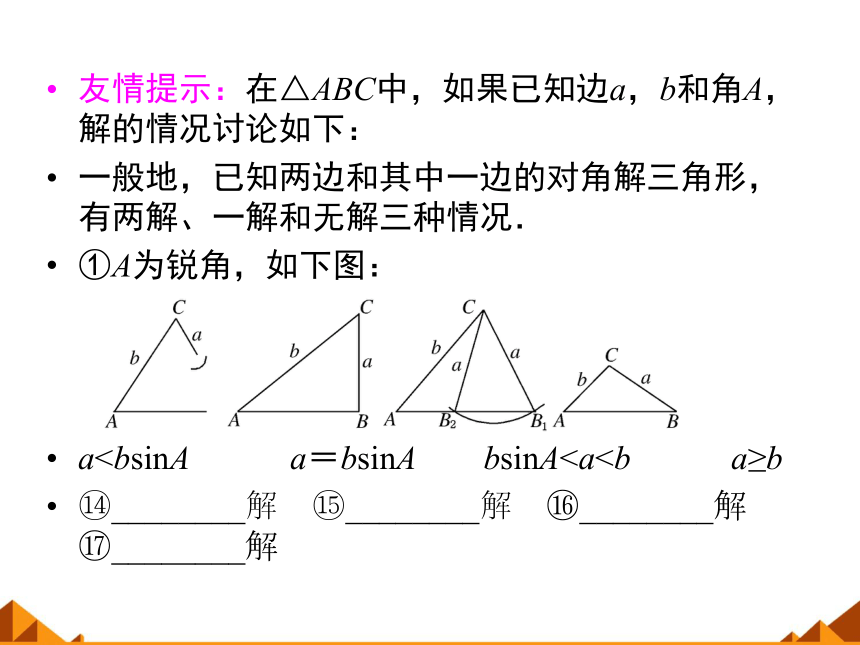
友情提示:在△ABC中,如果已知边a,b和角A,解的情况讨论如下:
一般地,已知两边和其中一边的对角解三角形,有两解、一解和无解三种情况.
①A为锐角,如下图:
a?________解 ?________解 ?________解 ?________解
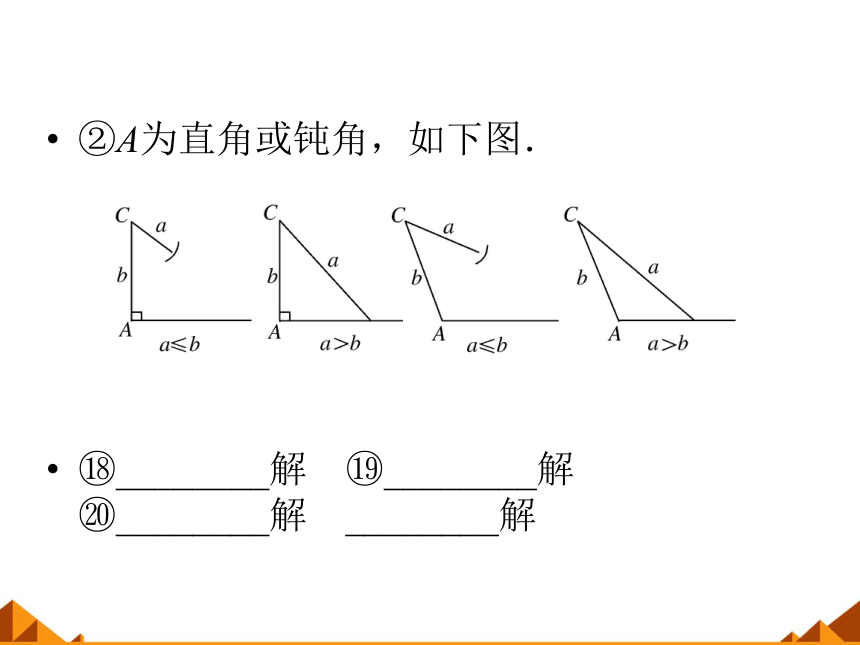
②A为直角或钝角,如下图.
?________解 ?________解 ?________解 ________解
归纳列表如下:
1.正弦定理的推导方法
对正弦定理的推导,我们可以从几何的角度进行推导.如图,以△ABC的顶点A为原点,边AC所在的射线为x轴的正半轴,建立直角坐标系.
另外,我们也可以从△ABC的外接圆来进行推导,如图.
当△ABC为直角三角形时,如图①所示,其外接圆的圆心O位于Rt△ABC的斜边AB上,R为外接圆的半径.
2.已知两边与其中一边的对角时,怎样确定三角形解的个数?
利用数形结合和三角函数知识来分析.例如:已知△ABC的两边a,b和角A解三角形时,有以下方法:
方法一:可以作图,利用数形结合加以说明.如下表所示:
具体解题时,作出已知角A,边长b,以点C为圆心,以边长a为半径画弧,与射线AB的公共点(除去顶点A)的个数即为三角形解的个数.
分析:从方程的观点看,正弦定理有三个等式,可视为三个方程,每个方程都含有四个量,知其三个量,便可求得第四个量.本题已知△ABC的两边和其中一边的对角,运用正弦定理可求出角A,然后再利用三角形内角和公式求得角C,进而求出边c.
[变式训练1] 在△ABC中,c=10,A=45°,C=30°,求a、b和B.
[例2] △ABC中,内角A、B、C的对边分别为a,b,c,已知b=5,∠B=30°,若c= ,解此三角形.
分析:主要考查用正、余弦定理解三角形及三角形中三角变形的技巧.
[例3] 在△ABC中,若b2sin2C+c2sin2B=2bccosB·cosC,试判断三角形的形状.
分析:已知条件中有边和角的混合关系,可考虑利用边化角,从角的关系判断,也可考虑角化边,从边的关系判断.
[变式训练3] 在△ABC中,若acosA=bcosB,求证:△ABC是等腰三角形或直角三角形.
分析:判断三角形形状通常从三角形内角的关系确定,也可以从三角形三边关系确定.本题可考虑把边化为角,寻找三角形角与角之间的关系,然后予以判定.
[例4] 如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.
(1)证明sinα+cos2β=0;
(2)若AC= DC,求β的值.
分析:根据等腰三角形的性质,内角和定理,结合三角公式,正、余弦定理即可解决.
解三角形的应用问题,通常都要根据题意,从实际问题中抽象出一个或几个三角形,然后通过解这些三角形,得出三角形的边和角的大小,从而得出实际问题的解.
[例5] (2009·辽宁卷)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01 km,
≈1.414, ≈2.449).
分析:本题考查了应用三角形知识求解实际问题的能力.求解此类解三角形问题首先要能够读懂题意,分析清楚题意,要能够将实际问题转化为数学问题,即解三角形问题.在具体求解过程中要能够明确三角形中的边角关系,同时要注意多解情况和计算的准确性.
解析:在△ACD中,∠DAC=30°,∠ADC=60°-∠DAC=30°,
所以CD=AC=0.1,
又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA.
[变式训练5] 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.
二、解三角形
1.解三角形时常用的结论
(1)在△ABC中,A>B?⑤________?⑥________;(即在一个三角形中大边对大角)
(2)a+b>c,b+c>a,⑦________;(即在一个三角形中两边之和大于第三边,两边之差小于第三边)
(3)内角和定理:△ABC中,A+B+C=⑧________.
2.正弦定理的应用
利用正弦定理可以解决以下两类有关三角形的问题:
(1)已知两角和任意一边,求其他⑨________和⑩________;
(2)已知两边和其中一边的对角,求?________,从而进一步求出其他的边和角.
对于第(1)类,其解是唯一确定的,一般先由三角形内角和为180°求得?________,再利用正弦定理求其余两边;
对于第(2)类,其解不一定唯一,由于三角形的形状不能唯一确定,因而会出现?________三种情况.
友情提示:在△ABC中,如果已知边a,b和角A,解的情况讨论如下:
一般地,已知两边和其中一边的对角解三角形,有两解、一解和无解三种情况.
①A为锐角,如下图:
a
②A为直角或钝角,如下图.
?________解 ?________解 ?________解 ________解
归纳列表如下:
1.正弦定理的推导方法
对正弦定理的推导,我们可以从几何的角度进行推导.如图,以△ABC的顶点A为原点,边AC所在的射线为x轴的正半轴,建立直角坐标系.
另外,我们也可以从△ABC的外接圆来进行推导,如图.
当△ABC为直角三角形时,如图①所示,其外接圆的圆心O位于Rt△ABC的斜边AB上,R为外接圆的半径.
2.已知两边与其中一边的对角时,怎样确定三角形解的个数?
利用数形结合和三角函数知识来分析.例如:已知△ABC的两边a,b和角A解三角形时,有以下方法:
方法一:可以作图,利用数形结合加以说明.如下表所示:
具体解题时,作出已知角A,边长b,以点C为圆心,以边长a为半径画弧,与射线AB的公共点(除去顶点A)的个数即为三角形解的个数.
分析:从方程的观点看,正弦定理有三个等式,可视为三个方程,每个方程都含有四个量,知其三个量,便可求得第四个量.本题已知△ABC的两边和其中一边的对角,运用正弦定理可求出角A,然后再利用三角形内角和公式求得角C,进而求出边c.
[变式训练1] 在△ABC中,c=10,A=45°,C=30°,求a、b和B.
[例2] △ABC中,内角A、B、C的对边分别为a,b,c,已知b=5,∠B=30°,若c= ,解此三角形.
分析:主要考查用正、余弦定理解三角形及三角形中三角变形的技巧.
[例3] 在△ABC中,若b2sin2C+c2sin2B=2bccosB·cosC,试判断三角形的形状.
分析:已知条件中有边和角的混合关系,可考虑利用边化角,从角的关系判断,也可考虑角化边,从边的关系判断.
[变式训练3] 在△ABC中,若acosA=bcosB,求证:△ABC是等腰三角形或直角三角形.
分析:判断三角形形状通常从三角形内角的关系确定,也可以从三角形三边关系确定.本题可考虑把边化为角,寻找三角形角与角之间的关系,然后予以判定.
[例4] 如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.
(1)证明sinα+cos2β=0;
(2)若AC= DC,求β的值.
分析:根据等腰三角形的性质,内角和定理,结合三角公式,正、余弦定理即可解决.
解三角形的应用问题,通常都要根据题意,从实际问题中抽象出一个或几个三角形,然后通过解这些三角形,得出三角形的边和角的大小,从而得出实际问题的解.
[例5] (2009·辽宁卷)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01 km,
≈1.414, ≈2.449).
分析:本题考查了应用三角形知识求解实际问题的能力.求解此类解三角形问题首先要能够读懂题意,分析清楚题意,要能够将实际问题转化为数学问题,即解三角形问题.在具体求解过程中要能够明确三角形中的边角关系,同时要注意多解情况和计算的准确性.
解析:在△ACD中,∠DAC=30°,∠ADC=60°-∠DAC=30°,
所以CD=AC=0.1,
又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA.
[变式训练5] 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.
