8.1正弦定理第二课时课件(共25张PPT)-湘教版数学必修4
文档属性
| 名称 | 8.1正弦定理第二课时课件(共25张PPT)-湘教版数学必修4 |

|
|
| 格式 | ppt | ||
| 文件大小 | 945.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 19:50:06 | ||
图片预览








文档简介
【课标要求】
理解正弦定理的推导过程,会初步运用正弦定理解斜三角形.
正弦定理
自学导引
1.
2.
锐角△ABC的外接圆O的半径为R,能否用R和角A表示a?在钝角△ABC中呢?
提示 能;均有a=2Rsin A
在△ABC中,为什么说A>B等价于sin A>sin B?
提示 A>B?a>b?2Rsin A>2Rsin B?sin A>sin B
自主探究
1.
2.
答案 7
答案 4
预习测评
△ABC中,p:sin AA.p?q B.q?p
C.q?p D.p q,q p
答案 C
3.
在△ABC中,下列关系中一定成立的是 ( ).
A.a>bsin A B.a=bsin A
C.a答案 D
4.
几何法证明正弦定理
教材中,用三角函数的定义给出正弦定理的证明,下面我们给出几何法证明,且引入三角形的外接圆半径,对以后解三角形非常有益.
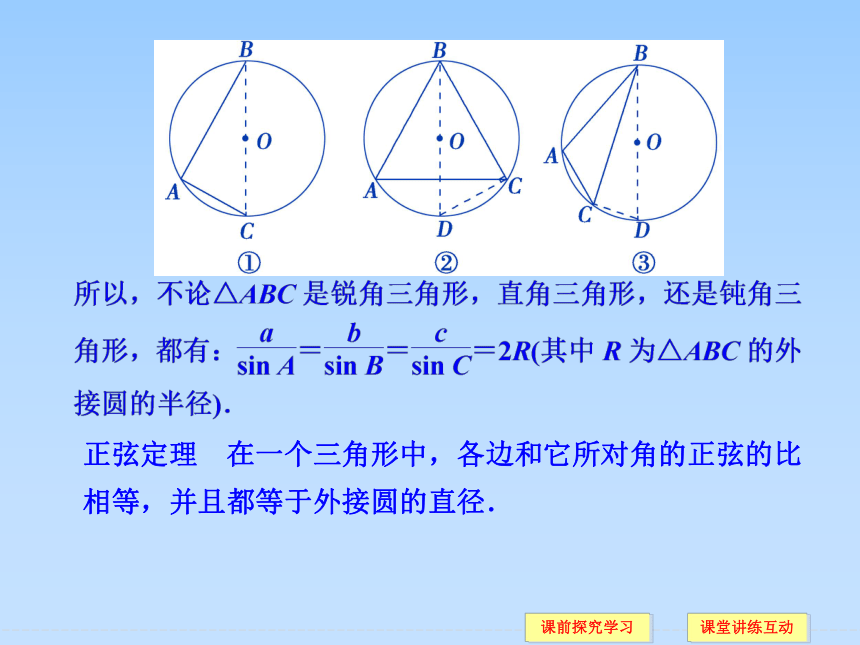
证明 设BD为△ABC外接圆⊙O的直径,则BD=2R,下面按∠A为直角、锐角、钝角三种情况加以证明.
名师点睛
1.
正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径.
特别提示 在用正弦定理解三角形时,经常用到以下三角关系式,请牢记并灵活地加以运用.
①A+B+C=π(在△ABC中,设角A、B、C的对边分别为a、b、c,下同);
②sin(A+B)=sin C,cos(A+B)=-cos C;
(1)已知两角和任意一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求另一边的对角,进而可求其他的边和角.
2.
已知两边和其中一边的对角,不能唯一确定三角形的形状,解这类三角形问题将出现无解、一解或两解三种情况,应分情况给予讨论.
下面为已知a,b和A,用正弦定理求解三角形时的各种情况:
①列表如下:
A为锐角
A为直角或钝角
图形
关系
式
a=bsin A
absin Aa≥b
a>b
解的
个数
一解
无解
两解
一解
一解
如果sin B>1,则问题无解;
如果sin B=1,则问题有一解;
如果求出sin B<1,则可得B的两个值,但要通过“三角形内角和定理”或“大边对大角”等三角形有关性质进行判断.
在△ABC中,a=5,B=45°,C=105°,求边c.
解 由三角形内角和定理知A+B+C=180°,
所以A=180°-(B+C)=180°-(45°+105°)=30°.
题型一 已知三角形的两角及一边解三角形
【例1】
典例剖析
方法点评 已知三角形的任意两角和任一边,均可解该三角形.本例中要注意在△ABC中,A+B+C=180°的运用.
已知三角形的两角分别是45°,60°,它们所夹边的长是1,求最小边的长.
解 设△ABC三内角A=45°,B=60°,则C=75°.
∵C>B>A,
∴最小边的长为a.
1.
A.45°或135° B.135° C.45° D.60°
答案 C
方法点评 利用正弦定理解三角形时,需注意“三角形”这个前提,如题目中根据“内角和为180°”,对求得的解进行检验.
题型二 已知两边及其一边的对角解三角形
【例2】
满足a=4,b=3和A=45°的△ABC的个数为 ( ).
A.0个 B.1个
C.2个 D.无数多个
解析 因为A=45°<90°,a=4>3=b,所以△ABC解的个数为一解,故选B.
答案 B
2.
在△ABC中,若acos A=bcos B,试判断△ABC的形状.
解 由正弦定理得,a=2Rsin A,b=2Rsin B,
∴由acos A=bcos B得:sin Acos A=sin Bcos B,
即sin 2A=sin 2B,
∵2A、2B∈(0,2π),∴2A=2B或2A=π-2B.
∴△ABC为等腰三角形或直角三角形.
方法点评 判断三角形的形状,一般方法就是“边角统一”,即化边为角或化角为边.
题型三 利用正弦定理判断三角形的形状
【例3】
∴b2-a2=ab ①
又2sin Asin B=2sin2C,由正弦定理得:
2ab=2c2 ②
由①②得b2=a2+c2.
所以该三角形是以B为直角顶点的直角三角形.
3.
误区警示 易出现丢解或多解的错误
【例4】
由研究特殊三角形到一般三角形,得出任意三角形的边、角之间的数量关系,即正弦定理的过程,是探讨数学问题常用的“从特殊到一般”的思想方法.
已知两角和任意一边,利用正弦定理解三角形,结果惟一;而已知两边和其中一边的对角,利用正弦定理解三角形,结果往往不确定,此时要根据图形或“大边对大角”作出判断.
课堂总结
2.
1.
3.
理解正弦定理的推导过程,会初步运用正弦定理解斜三角形.
正弦定理
自学导引
1.
2.
锐角△ABC的外接圆O的半径为R,能否用R和角A表示a?在钝角△ABC中呢?
提示 能;均有a=2Rsin A
在△ABC中,为什么说A>B等价于sin A>sin B?
提示 A>B?a>b?2Rsin A>2Rsin B?sin A>sin B
自主探究
1.
2.
答案 7
答案 4
预习测评
△ABC中,p:sin A
C.q?p D.p q,q p
答案 C
3.
在△ABC中,下列关系中一定成立的是 ( ).
A.a>bsin A B.a=bsin A
C.a
4.
几何法证明正弦定理
教材中,用三角函数的定义给出正弦定理的证明,下面我们给出几何法证明,且引入三角形的外接圆半径,对以后解三角形非常有益.
证明 设BD为△ABC外接圆⊙O的直径,则BD=2R,下面按∠A为直角、锐角、钝角三种情况加以证明.
名师点睛
1.
正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径.
特别提示 在用正弦定理解三角形时,经常用到以下三角关系式,请牢记并灵活地加以运用.
①A+B+C=π(在△ABC中,设角A、B、C的对边分别为a、b、c,下同);
②sin(A+B)=sin C,cos(A+B)=-cos C;
(1)已知两角和任意一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求另一边的对角,进而可求其他的边和角.
2.
已知两边和其中一边的对角,不能唯一确定三角形的形状,解这类三角形问题将出现无解、一解或两解三种情况,应分情况给予讨论.
下面为已知a,b和A,用正弦定理求解三角形时的各种情况:
①列表如下:
A为锐角
A为直角或钝角
图形
关系
式
a=bsin A
a
a>b
解的
个数
一解
无解
两解
一解
一解
如果sin B>1,则问题无解;
如果sin B=1,则问题有一解;
如果求出sin B<1,则可得B的两个值,但要通过“三角形内角和定理”或“大边对大角”等三角形有关性质进行判断.
在△ABC中,a=5,B=45°,C=105°,求边c.
解 由三角形内角和定理知A+B+C=180°,
所以A=180°-(B+C)=180°-(45°+105°)=30°.
题型一 已知三角形的两角及一边解三角形
【例1】
典例剖析
方法点评 已知三角形的任意两角和任一边,均可解该三角形.本例中要注意在△ABC中,A+B+C=180°的运用.
已知三角形的两角分别是45°,60°,它们所夹边的长是1,求最小边的长.
解 设△ABC三内角A=45°,B=60°,则C=75°.
∵C>B>A,
∴最小边的长为a.
1.
A.45°或135° B.135° C.45° D.60°
答案 C
方法点评 利用正弦定理解三角形时,需注意“三角形”这个前提,如题目中根据“内角和为180°”,对求得的解进行检验.
题型二 已知两边及其一边的对角解三角形
【例2】
满足a=4,b=3和A=45°的△ABC的个数为 ( ).
A.0个 B.1个
C.2个 D.无数多个
解析 因为A=45°<90°,a=4>3=b,所以△ABC解的个数为一解,故选B.
答案 B
2.
在△ABC中,若acos A=bcos B,试判断△ABC的形状.
解 由正弦定理得,a=2Rsin A,b=2Rsin B,
∴由acos A=bcos B得:sin Acos A=sin Bcos B,
即sin 2A=sin 2B,
∵2A、2B∈(0,2π),∴2A=2B或2A=π-2B.
∴△ABC为等腰三角形或直角三角形.
方法点评 判断三角形的形状,一般方法就是“边角统一”,即化边为角或化角为边.
题型三 利用正弦定理判断三角形的形状
【例3】
∴b2-a2=ab ①
又2sin Asin B=2sin2C,由正弦定理得:
2ab=2c2 ②
由①②得b2=a2+c2.
所以该三角形是以B为直角顶点的直角三角形.
3.
误区警示 易出现丢解或多解的错误
【例4】
由研究特殊三角形到一般三角形,得出任意三角形的边、角之间的数量关系,即正弦定理的过程,是探讨数学问题常用的“从特殊到一般”的思想方法.
已知两角和任意一边,利用正弦定理解三角形,结果惟一;而已知两边和其中一边的对角,利用正弦定理解三角形,结果往往不确定,此时要根据图形或“大边对大角”作出判断.
课堂总结
2.
1.
3.
