9.2.1 等差数列课件-湘教版数学必修4(23张PPT)
文档属性
| 名称 | 9.2.1 等差数列课件-湘教版数学必修4(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 359.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览







文档简介
9.2.1 等差数列
学习
目标
数学建模
数学运算
直观想象
渗透
核心
素养
逻辑推理
数学抽象
数据分析
01
通过观察实例,能够抽象出等差数列的概念;
能根据定义判断一个数列是等差数列
02
通过自主学习和小组合作交流,
推导出等差数列的通项公式;
03
能够准确利用通项公式做到知三求一,
渗透方程思想;
04
能够正确理解等差数列与函数的
具体关系.
案例1:
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:1682,1758,1834,1910,1986,…...
( )
2062
相差76
问题1:你能预测出彗星下一次出现的大致时间吗?
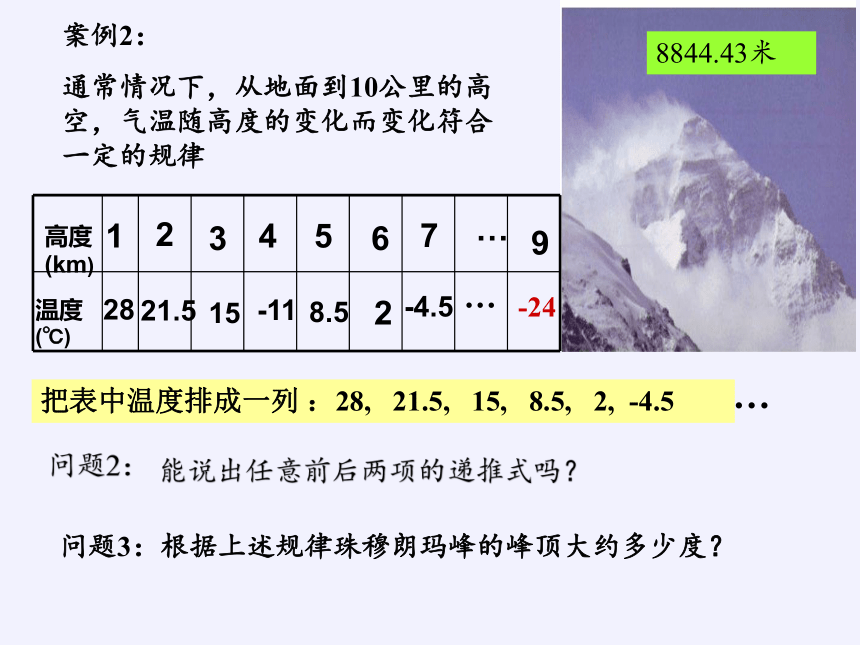
案例2:
通常情况下,从地面到10公里的高空,气温随高度的变化而变化符合一定的规律
8844.43米
把表中温度排成一列 :28, 21.5, 15, 8.5, 2, -4.5
…
-24
高度(km)
温度(℃)
1
2
3
28
21.5
15
7
-11
4
5
8.5
2
6
-4.5
9
…
问题2:
问题3:根据上述规律珠穆朗玛峰的峰顶大约多少度?
…
能说出任意前后两项的递推式吗?
思考1:它们有什么共同特点?
共同特点:从第2项起,每一项与它的前一项的差等于同一个常数。
定义:如果一个数列从第2项起,每一项与它的前一项 的差都等于同一个常数,那么这个数列就叫做等差数列.
这个常数叫做等差数列的公差,公差通常用 d 表示.
(4)5,5,5,5,5,…
(1)1682,1758,1834,1910,1986,
(3)1,2,3, …100, …
(2) 28, 21.5, 15, 8.5, 2, …, -24.
【新知探究1】
探究1:等差数列的定义
思考2:如何用数学符号来描述等差数列的定义?
思考3:它们是等差数列吗?判定的依据是什么?
(5)
数列{ an }为等差数列?
an+1-an=d(n≥1)
(1) 0,5,10,15,20,25,…
(2)48,53,58,63.
(3)1, 3, 5, 7, 9, 2, 4, 6, 8, 10
(4)16,8,4,2,1…
(奥运会女子举重级别(单位公斤))
1,4,7,10,13,16,( ),( )……
思考4:根据规律填空?如何才能求出数列第n项呢?
新知探究2:等差数列的通项公式
要是有通项公式该有多好啊!
19
22
从特殊入手,研究数学对象的性质,
再逐步扩展到一般,这是数学研究的常用方法
思考5:如何推导等差数列的通项公式
如果一个数列
是等差数列,它的公差是d,那么
…,
…
通项公式:
【新知探究2】
{5940675A-B579-460E-94D1-54222C63F5DA}①能够直观感知哪些是等差数列,可以写出一些简单等差数列的通项公式
?( )
?
②能清晰描述等差数列特征,能用严谨的数学符号推导等差数列的通项公式?( )
③能理解并阐述等差数列的概念,且能熟练灵活使用术语、符号描述等差数列,并能用多种思维方式推导通项公式?( )
【过程评价1】选择贴合自己的情况打√
1. 求等差数列3,7,11,…的第4,7,10项;
2. 100是不是等差数列2,9,16,…中的项?
3. -20是不是等差数列0,- ,-7,…中的项;
【迁移应用】通项公式的应用
例1
思考6:如何求出数列中的某一项?如何判断一数是否为某一数列的其中一项?
思考:等差数列的图像是否是一条直线呢?
思考7.
【迁移应用】
思考:能否说等差数列{an} 通项公式是关于n的一次函数呢?
等差数列的图象1
(1)数列:-2,0,2,4,6,8,10,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
是一
群在
一条
直线
上的
孤立
的点
在等差数列通项公式中,有四个量,
知道其中的任意三个量,就可以求出另一个量,即知三求一 .
思考:能否从方程的角度理解通项公式?
【迁移应用】
变式1:在等差数列中,已知a5=10,a12=31,
求首项a1与公差d.
说明:由此可以看到:已知等差数列的两项就
可以确定这个数列.
变式2:已知数列{an},an=3n-4,{an}是等差数列吗?
{5940675A-B579-460E-94D1-54222C63F5DA}①能熟练应用通项公式求解首项,公差,项数、通项,各项?( )
②能感悟出数列与函数方程的关系,并能树立“知三求一”的方程意识? ( )
③能以函数方程的观点来理解等差数列及通项公式的意义,并能用严谨的数学语言阐释原理;可以多角度、辩证的理解等差数列并能灵活应用( )
【过程评价2】选择贴合自己的情况打√
逆向
原点
基于理解的逆向学习
目标
【新知巩固】
本节课学习的主要内容有:
一个定义
一个公式
一个重点:知三求一
一个思想:
【总结收获】
达成目标
数学建模
数学运算
直观想象
渗透
核心
素养
逻辑推理
数学抽象
数据分析
01
通过观察实例,能够抽象出等差数列的概念;
能根据定义判断一个数列是等差数列
02
通过自主学习和小组合作交流,
推导出等差数列的通项公式;
03
能够准确利用通项公式做到知三求一,
渗透方程思想;
04
能够正确理解等差数列与函数的
具体关系.
A层作业:请同学们完成课后的习题。
B层作业:(请用思维导图的方式进行整理)
C层选作: 在线答疑:
谢谢 再见
谢 谢
学习
目标
数学建模
数学运算
直观想象
渗透
核心
素养
逻辑推理
数学抽象
数据分析
01
通过观察实例,能够抽象出等差数列的概念;
能根据定义判断一个数列是等差数列
02
通过自主学习和小组合作交流,
推导出等差数列的通项公式;
03
能够准确利用通项公式做到知三求一,
渗透方程思想;
04
能够正确理解等差数列与函数的
具体关系.
案例1:
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:1682,1758,1834,1910,1986,…...
( )
2062
相差76
问题1:你能预测出彗星下一次出现的大致时间吗?
案例2:
通常情况下,从地面到10公里的高空,气温随高度的变化而变化符合一定的规律
8844.43米
把表中温度排成一列 :28, 21.5, 15, 8.5, 2, -4.5
…
-24
高度(km)
温度(℃)
1
2
3
28
21.5
15
7
-11
4
5
8.5
2
6
-4.5
9
…
问题2:
问题3:根据上述规律珠穆朗玛峰的峰顶大约多少度?
…
能说出任意前后两项的递推式吗?
思考1:它们有什么共同特点?
共同特点:从第2项起,每一项与它的前一项的差等于同一个常数。
定义:如果一个数列从第2项起,每一项与它的前一项 的差都等于同一个常数,那么这个数列就叫做等差数列.
这个常数叫做等差数列的公差,公差通常用 d 表示.
(4)5,5,5,5,5,…
(1)1682,1758,1834,1910,1986,
(3)1,2,3, …100, …
(2) 28, 21.5, 15, 8.5, 2, …, -24.
【新知探究1】
探究1:等差数列的定义
思考2:如何用数学符号来描述等差数列的定义?
思考3:它们是等差数列吗?判定的依据是什么?
(5)
数列{ an }为等差数列?
an+1-an=d(n≥1)
(1) 0,5,10,15,20,25,…
(2)48,53,58,63.
(3)1, 3, 5, 7, 9, 2, 4, 6, 8, 10
(4)16,8,4,2,1…
(奥运会女子举重级别(单位公斤))
1,4,7,10,13,16,( ),( )……
思考4:根据规律填空?如何才能求出数列第n项呢?
新知探究2:等差数列的通项公式
要是有通项公式该有多好啊!
19
22
从特殊入手,研究数学对象的性质,
再逐步扩展到一般,这是数学研究的常用方法
思考5:如何推导等差数列的通项公式
如果一个数列
是等差数列,它的公差是d,那么
…,
…
通项公式:
【新知探究2】
{5940675A-B579-460E-94D1-54222C63F5DA}①能够直观感知哪些是等差数列,可以写出一些简单等差数列的通项公式
?( )
?
②能清晰描述等差数列特征,能用严谨的数学符号推导等差数列的通项公式?( )
③能理解并阐述等差数列的概念,且能熟练灵活使用术语、符号描述等差数列,并能用多种思维方式推导通项公式?( )
【过程评价1】选择贴合自己的情况打√
1. 求等差数列3,7,11,…的第4,7,10项;
2. 100是不是等差数列2,9,16,…中的项?
3. -20是不是等差数列0,- ,-7,…中的项;
【迁移应用】通项公式的应用
例1
思考6:如何求出数列中的某一项?如何判断一数是否为某一数列的其中一项?
思考:等差数列的图像是否是一条直线呢?
思考7.
【迁移应用】
思考:能否说等差数列{an} 通项公式是关于n的一次函数呢?
等差数列的图象1
(1)数列:-2,0,2,4,6,8,10,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
是一
群在
一条
直线
上的
孤立
的点
在等差数列通项公式中,有四个量,
知道其中的任意三个量,就可以求出另一个量,即知三求一 .
思考:能否从方程的角度理解通项公式?
【迁移应用】
变式1:在等差数列中,已知a5=10,a12=31,
求首项a1与公差d.
说明:由此可以看到:已知等差数列的两项就
可以确定这个数列.
变式2:已知数列{an},an=3n-4,{an}是等差数列吗?
{5940675A-B579-460E-94D1-54222C63F5DA}①能熟练应用通项公式求解首项,公差,项数、通项,各项?( )
②能感悟出数列与函数方程的关系,并能树立“知三求一”的方程意识? ( )
③能以函数方程的观点来理解等差数列及通项公式的意义,并能用严谨的数学语言阐释原理;可以多角度、辩证的理解等差数列并能灵活应用( )
【过程评价2】选择贴合自己的情况打√
逆向
原点
基于理解的逆向学习
目标
【新知巩固】
本节课学习的主要内容有:
一个定义
一个公式
一个重点:知三求一
一个思想:
【总结收获】
达成目标
数学建模
数学运算
直观想象
渗透
核心
素养
逻辑推理
数学抽象
数据分析
01
通过观察实例,能够抽象出等差数列的概念;
能根据定义判断一个数列是等差数列
02
通过自主学习和小组合作交流,
推导出等差数列的通项公式;
03
能够准确利用通项公式做到知三求一,
渗透方程思想;
04
能够正确理解等差数列与函数的
具体关系.
A层作业:请同学们完成课后的习题。
B层作业:(请用思维导图的方式进行整理)
C层选作: 在线答疑:
谢谢 再见
谢 谢
