8.3解三角形的应用举例_课件-湘教版数学必修4(23张PPT)
文档属性
| 名称 | 8.3解三角形的应用举例_课件-湘教版数学必修4(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 09:06:39 | ||
图片预览






文档简介
1.正弦定理:
复习回顾
2.余弦定理和推论:
3.三角形边与角的关系:
2、 大角对大边,小角对小边 。
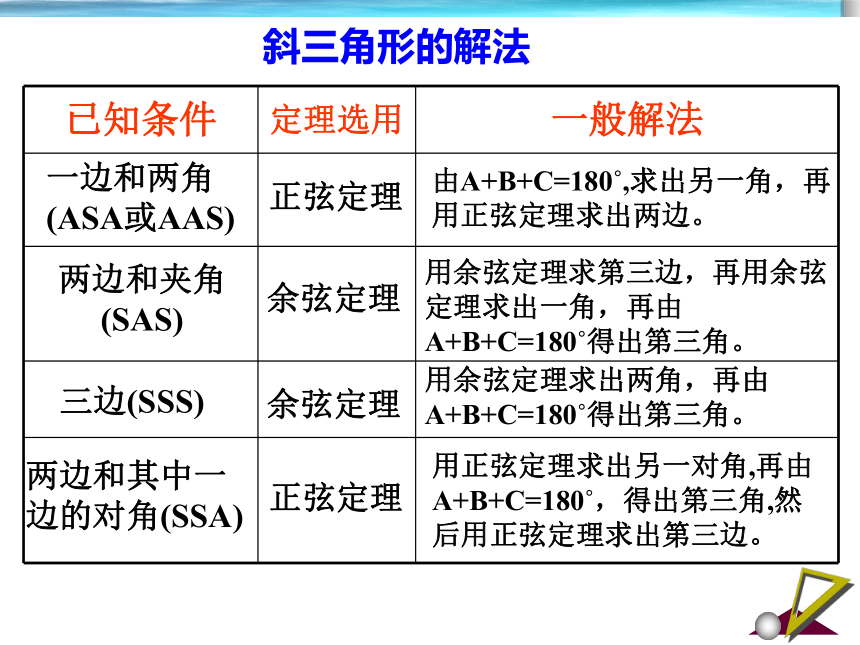
斜三角形的解法
已知条件
定理选用
一般解法
用正弦定理求出另一对角,再由A+B+C=180?,得出第三角,然后用正弦定理求出第三边。
正弦定理
余弦定理
正弦定理
余弦定理
由A+B+C=180?,求出另一角,再用正弦定理求出两边。
用余弦定理求第三边,再用余弦定理求出一角,再由A+B+C=180?得出第三角。
用余弦定理求出两角,再由A+B+C=180?得出第三角。
一边和两角
(ASA或AAS)
两边和夹角(SAS)
三边(SSS)
两边和其中一
边的对角(SSA)
高度
角度
距离
有关三角形计算
高度和角度的测量
经纬仪,测量水平角和竖直角的仪器。
是根据测角原理设计的。目前最常用
的是光学经纬仪。
光学经纬仪
钢卷尺
实例讲解
解:根据正弦定理,得
答:A,B两点间的距离为65.7米。
练习1.如图在铁路建设中需要确定隧道两端A,B的距离,请你设计一种测量A,B距离的方法?
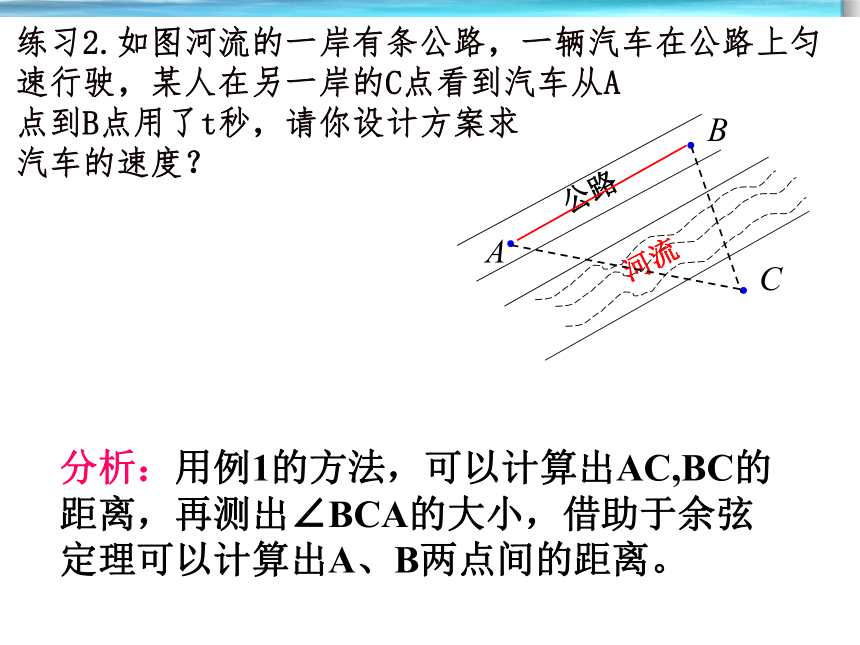
练习2.如图河流的一岸有条公路,一辆汽车在公路上匀速行驶,某人在另一岸的C点看到汽车从A
点到B点用了t秒,请你设计方案求
汽车的速度?
分析:用例1的方法,可以计算出AC,BC的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。
公路
河流
公路
河流
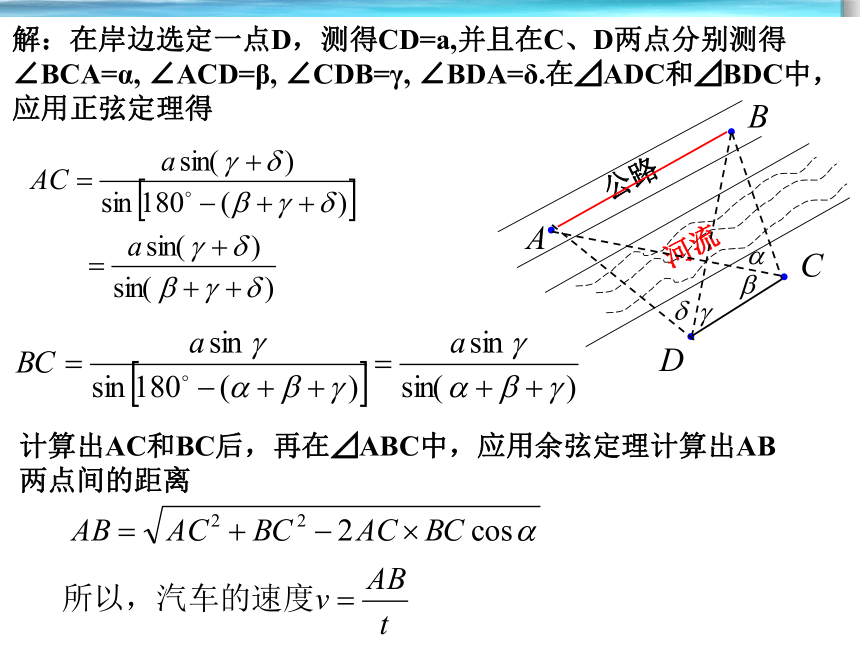
解:在岸边选定一点D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在⊿ADC和⊿BDC中,应用正弦定理得
计算出AC和BC后,再在⊿ABC中,应用余弦定理计算出AB两点间的距离
测量问题之一:
水平距离的测量
①两点间不能到达,又不能相互看到。(如图1所示)
需要测量CB、CA的长和角C的大小,由余弦定理,可求得AB的长。
②两点能相互看到,但不能到达。(如图2所示)
需要测量BC的长、角B和角C的大小,由三角形的内角和,求出角A然后由正弦定理,可求边AB的长。
图1
图2
③两点都不能到达
1、分析:理解题意,画出示意图
2、建模:把已知量与求解量集中在一个三角形中
3、求解:运用正弦定理和余弦定理,有顺序地解这些三子角形,求得数学模型的解。
4、检验:检验所求的解是否符合实际意义,从而得出实际问题的解。
实际问题→数学问题(三角形)
→数学问题的解(解三角形)→实际问题的解
解应用题的一般步骤是:
小结
解应用题中的几个角的概念
1、仰角、俯角的概念:
在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。如图:
2、方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,如图
测量垂直高度
1、底部可以到达的
测量出角C和BC的长度,解直角三角形即可求出AB的长。
2、对底部不能到达的 怎么办?
图中给出了怎样的一个
几何图形?已知什么,
求什么?
想一想
B
E
A
G
H
D
C
2、底部不能到达的
练习1: 在山顶铁塔上B处测得地面上一点A的俯角α= 60° ,在塔底C处测得A处的俯角β=30°。已知铁塔BC部分的高为28m,求出山高CD.
分析:根据已知条件,应该设法计算出AB或AC的长
D
A
B
C
?
?
CD=BD-BC=42-28=14(m)
答:山的高度约为14米。
解:在⊿ABC中,∠BCA=90°+β, ∠ABC=90°-α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,
例2 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北测远处一山顶D在西偏北15?的方向上,行驶5km后到达B处,测得此山顶在西偏北25?的方向上,仰角为8?,求此山的高度CD.
例4、某巡逻艇在A处发现北偏东450相距9海里的C处有
一艘走私船,正沿南偏东750的方向以10海里/小时的速
度向我海岸行驶,巡逻艇立即以14海里/小时的速度沿
着直线方向追去,问巡逻艇应该沿什么方向去追?需要
多少时间才追赶上该走私船?
答:巡逻艇应该沿北偏东830方向去追,经过1.5小时才追赶上
该走私船.
1、在某点B处测得建筑物AE的顶端A的仰角为 ,
沿BE方向前进30m,至点C处测得顶端A的仰角为2 ,
再继续前进10 m至D点,测得顶端A的仰角为4 ,
求 的大小和建筑物AE的高。
课堂小结
1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。
2、在分析问题解决问题的过程中关键要分析题意,分清已知
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。
3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:
实际问题
数学模型
实际问题的解
数学模型的解
画图形
解三角形
检验(答)
复习回顾
2.余弦定理和推论:
3.三角形边与角的关系:
2、 大角对大边,小角对小边 。
斜三角形的解法
已知条件
定理选用
一般解法
用正弦定理求出另一对角,再由A+B+C=180?,得出第三角,然后用正弦定理求出第三边。
正弦定理
余弦定理
正弦定理
余弦定理
由A+B+C=180?,求出另一角,再用正弦定理求出两边。
用余弦定理求第三边,再用余弦定理求出一角,再由A+B+C=180?得出第三角。
用余弦定理求出两角,再由A+B+C=180?得出第三角。
一边和两角
(ASA或AAS)
两边和夹角(SAS)
三边(SSS)
两边和其中一
边的对角(SSA)
高度
角度
距离
有关三角形计算
高度和角度的测量
经纬仪,测量水平角和竖直角的仪器。
是根据测角原理设计的。目前最常用
的是光学经纬仪。
光学经纬仪
钢卷尺
实例讲解
解:根据正弦定理,得
答:A,B两点间的距离为65.7米。
练习1.如图在铁路建设中需要确定隧道两端A,B的距离,请你设计一种测量A,B距离的方法?
练习2.如图河流的一岸有条公路,一辆汽车在公路上匀速行驶,某人在另一岸的C点看到汽车从A
点到B点用了t秒,请你设计方案求
汽车的速度?
分析:用例1的方法,可以计算出AC,BC的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。
公路
河流
公路
河流
解:在岸边选定一点D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在⊿ADC和⊿BDC中,应用正弦定理得
计算出AC和BC后,再在⊿ABC中,应用余弦定理计算出AB两点间的距离
测量问题之一:
水平距离的测量
①两点间不能到达,又不能相互看到。(如图1所示)
需要测量CB、CA的长和角C的大小,由余弦定理,可求得AB的长。
②两点能相互看到,但不能到达。(如图2所示)
需要测量BC的长、角B和角C的大小,由三角形的内角和,求出角A然后由正弦定理,可求边AB的长。
图1
图2
③两点都不能到达
1、分析:理解题意,画出示意图
2、建模:把已知量与求解量集中在一个三角形中
3、求解:运用正弦定理和余弦定理,有顺序地解这些三子角形,求得数学模型的解。
4、检验:检验所求的解是否符合实际意义,从而得出实际问题的解。
实际问题→数学问题(三角形)
→数学问题的解(解三角形)→实际问题的解
解应用题的一般步骤是:
小结
解应用题中的几个角的概念
1、仰角、俯角的概念:
在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。如图:
2、方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,如图
测量垂直高度
1、底部可以到达的
测量出角C和BC的长度,解直角三角形即可求出AB的长。
2、对底部不能到达的 怎么办?
图中给出了怎样的一个
几何图形?已知什么,
求什么?
想一想
B
E
A
G
H
D
C
2、底部不能到达的
练习1: 在山顶铁塔上B处测得地面上一点A的俯角α= 60° ,在塔底C处测得A处的俯角β=30°。已知铁塔BC部分的高为28m,求出山高CD.
分析:根据已知条件,应该设法计算出AB或AC的长
D
A
B
C
?
?
CD=BD-BC=42-28=14(m)
答:山的高度约为14米。
解:在⊿ABC中,∠BCA=90°+β, ∠ABC=90°-α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,
例2 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北测远处一山顶D在西偏北15?的方向上,行驶5km后到达B处,测得此山顶在西偏北25?的方向上,仰角为8?,求此山的高度CD.
例4、某巡逻艇在A处发现北偏东450相距9海里的C处有
一艘走私船,正沿南偏东750的方向以10海里/小时的速
度向我海岸行驶,巡逻艇立即以14海里/小时的速度沿
着直线方向追去,问巡逻艇应该沿什么方向去追?需要
多少时间才追赶上该走私船?
答:巡逻艇应该沿北偏东830方向去追,经过1.5小时才追赶上
该走私船.
1、在某点B处测得建筑物AE的顶端A的仰角为 ,
沿BE方向前进30m,至点C处测得顶端A的仰角为2 ,
再继续前进10 m至D点,测得顶端A的仰角为4 ,
求 的大小和建筑物AE的高。
课堂小结
1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。
2、在分析问题解决问题的过程中关键要分析题意,分清已知
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。
3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:
实际问题
数学模型
实际问题的解
数学模型的解
画图形
解三角形
检验(答)
