10.1不等式的基本性质_课件-湘教版数学必修4(30张PPT)
文档属性
| 名称 | 10.1不等式的基本性质_课件-湘教版数学必修4(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 956.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 09:14:20 | ||
图片预览










文档简介
人与人的年龄大小、高矮胖瘦,物与物的形状结构,事与事的成因与结果的不同等等都表现出不等关系,这表明现实世界中的量,不等是普遍的、绝对的,而相等则是局部的、相对的。
不等式知识贯穿整个高中数学,也是高等数学的基础和工具,一直是高考的重点内容,占相当大的比重。不等式具有应用广泛、变换灵活的特点。
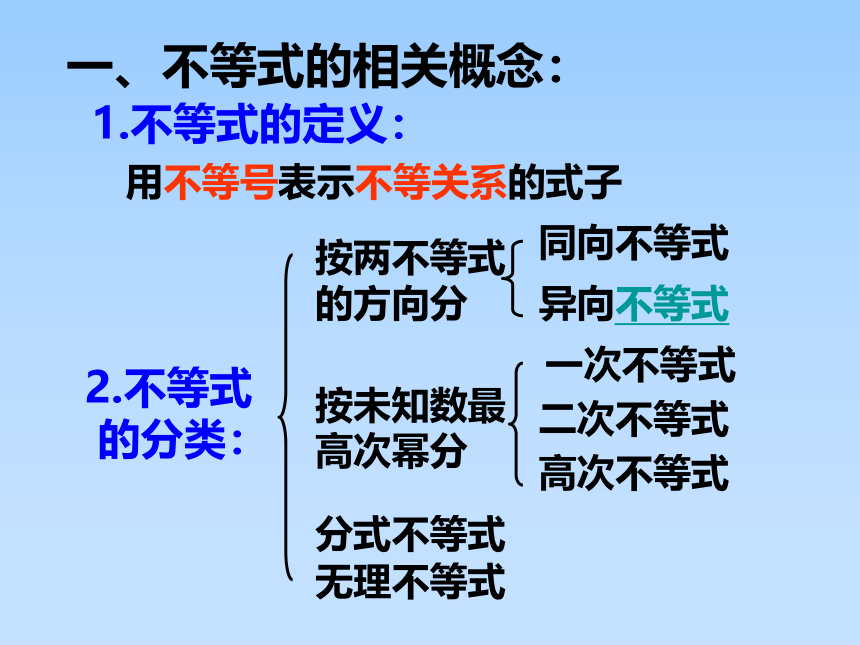
一、不等式的相关概念:
1.不等式的定义:
用不等号表示不等关系的式子
2.不等式
的分类:
按两不等式的方向分
同向不等式
异向不等式
按未知数最高次幂分
一次不等式
二次不等式
高次不等式
无理不等式
分式不等式
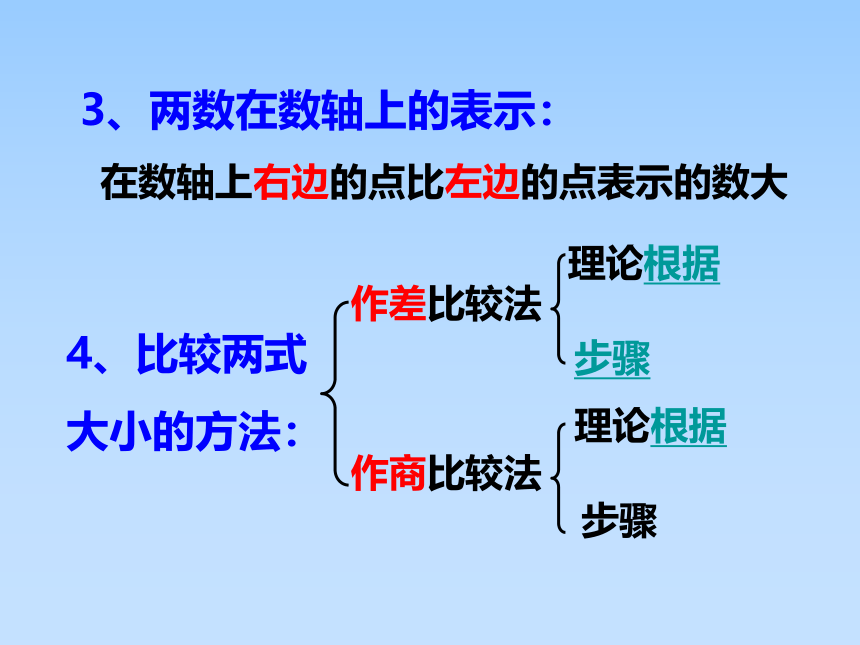
3、两数在数轴上的表示:
在数轴上右边的点比左边的点表示的数大
4、比较两式
大小的方法:
作差比较法
作商比较法
理论根据
步骤
理论根据
步骤
二、不等式的性质
1、对称性:
2、传递性:
3、加法性质:
同向可加性
二、不等式的性质
4、乘法性质:
5、乘方性质:
( 取正整数)
同向同正可乘
二、不等式的性质
6、开方性质:
( 取正整数)
7、倒数性质:
例1:已知 ,那么在
这三个数中,最小的数是
____,最大的数是_______
三、例题分析:
解法1:
特殊值法
用于简单判断或填空题
解法2:
作差比较法
例2:(1)已知 ,则
从小到大的顺序是
______________________
三、例题分析:
特殊值法: 取
例2:(2)已知 ,比较
与 的大小__________
三、例题分析:
作差比较法:
(条件 的应用)
(配方)
注:特殊值法容易漏“=”
小结:
作差比较两数大小的步骤
(1)作差;
(2)变形;
(3)定号;
(4)下结论;
常用手段:配方法,因式分
解法
三、例题分析:
作差比较法:
例3:已知 ,比较
与 的大小。
(分组)
(定号)
(通分)
三、例题分析:
解法1:(作差法)
例4:已知 ,比较
与 的大小。
(分组通分)
(定号)
三、例题分析:
解法2:(作商法)
例4:已知 ,比较
与 的大小。
(定号)
(立方和公式)
(配方)
三、例题分析:
解法3:(平方作差法)
例4:已知 ,比较
与 的大小。
立方和变形
小结:
作差比较大小(变形是关键)
变形
常见形式:变形为常数;
一个常数与几
个平方和;
几个因式的积
常用手段:配方法,因式分
解法
注:平方差,完全平方,立方和、 差等公式的应用
三、例题分析:
解:
例5:已知 ,求
的取值范围。
(加法法则-同向可加性)
(乘法单调性)
(加法法则)
三、例题分析:
解:
例5:已知 ,求
的取值范围。
(倒数法则)
(乘法单调性)
(乘法法则)
(乘法单调性)
三、例题分析:
解:
例5:已知 ,求
的取值范围。
(乘法单调性)
(乘法法则)
(乘法单调性)
三、例题分析:
解:
例5:已知 ,求
的取值范围。
(乘方法则)
(倒数法则)
(乘法法则)
注意:
在求解过程中要避免犯如下错误:
得
由
错因:用乘法法则时不符合其
“同向同正”的前提条件。
小结
主要内容
基本理论:
a - b > 0 <=> a > b
a - b = 0 <=> a = b
a - b < 0 <=> a < b
基本理论应用之一:比较实数的大小.
一般步骤:
作差-变形-判断符号-下结论
1°变形常用手段:配方法,因式分解法
2°变形常见形式是:变形为常数;
一个常数与几个平方和;几个因式的积
1.基本概念
同向不等式:
在两个不等式中,如果每一个的左边都大于右边,或每一个的左边都小于右边.
异向不等式:
在两个不等式中,如果一个不等式的左边大于右边,而另一个的左边小于右边.
作差比较两数大小的依据
上式中的左边反映的是实数的运算性质,而右边则是实数的大小顺序,合起来就成为实数的运算性质与大小顺序之间的关系。这一性质不仅可以用来比较两个实数的大小,而且是推导不等式的性质,不等式的证明,解不等式的主要依据。
判断两个实数a与b的大小,归结为判断它们的差a-b 的符号,从而归结为实数运算的符号法则,分三步进行:
作差比较两数大小的步骤
(1)作差;
(2)变形;
(3)定号;
(4)下结论;
常用手段:配方法,因式分
解法。
常见形式:变形为常数;
一个常数与几
个平方和;
几个因式的积。
作商比较两数大小的依据
若
例1:已知 ,那么在
这三个数中,最小的数是
____,最大的数是_______
解法1:
令
则
例1:已知 ,那么在
这三个数中,最小的数是
____,最大的数是_______
解法2:
化成若干因式相乘除来定号
化成若干因式相乘除来定号
不等式知识贯穿整个高中数学,也是高等数学的基础和工具,一直是高考的重点内容,占相当大的比重。不等式具有应用广泛、变换灵活的特点。
一、不等式的相关概念:
1.不等式的定义:
用不等号表示不等关系的式子
2.不等式
的分类:
按两不等式的方向分
同向不等式
异向不等式
按未知数最高次幂分
一次不等式
二次不等式
高次不等式
无理不等式
分式不等式
3、两数在数轴上的表示:
在数轴上右边的点比左边的点表示的数大
4、比较两式
大小的方法:
作差比较法
作商比较法
理论根据
步骤
理论根据
步骤
二、不等式的性质
1、对称性:
2、传递性:
3、加法性质:
同向可加性
二、不等式的性质
4、乘法性质:
5、乘方性质:
( 取正整数)
同向同正可乘
二、不等式的性质
6、开方性质:
( 取正整数)
7、倒数性质:
例1:已知 ,那么在
这三个数中,最小的数是
____,最大的数是_______
三、例题分析:
解法1:
特殊值法
用于简单判断或填空题
解法2:
作差比较法
例2:(1)已知 ,则
从小到大的顺序是
______________________
三、例题分析:
特殊值法: 取
例2:(2)已知 ,比较
与 的大小__________
三、例题分析:
作差比较法:
(条件 的应用)
(配方)
注:特殊值法容易漏“=”
小结:
作差比较两数大小的步骤
(1)作差;
(2)变形;
(3)定号;
(4)下结论;
常用手段:配方法,因式分
解法
三、例题分析:
作差比较法:
例3:已知 ,比较
与 的大小。
(分组)
(定号)
(通分)
三、例题分析:
解法1:(作差法)
例4:已知 ,比较
与 的大小。
(分组通分)
(定号)
三、例题分析:
解法2:(作商法)
例4:已知 ,比较
与 的大小。
(定号)
(立方和公式)
(配方)
三、例题分析:
解法3:(平方作差法)
例4:已知 ,比较
与 的大小。
立方和变形
小结:
作差比较大小(变形是关键)
变形
常见形式:变形为常数;
一个常数与几
个平方和;
几个因式的积
常用手段:配方法,因式分
解法
注:平方差,完全平方,立方和、 差等公式的应用
三、例题分析:
解:
例5:已知 ,求
的取值范围。
(加法法则-同向可加性)
(乘法单调性)
(加法法则)
三、例题分析:
解:
例5:已知 ,求
的取值范围。
(倒数法则)
(乘法单调性)
(乘法法则)
(乘法单调性)
三、例题分析:
解:
例5:已知 ,求
的取值范围。
(乘法单调性)
(乘法法则)
(乘法单调性)
三、例题分析:
解:
例5:已知 ,求
的取值范围。
(乘方法则)
(倒数法则)
(乘法法则)
注意:
在求解过程中要避免犯如下错误:
得
由
错因:用乘法法则时不符合其
“同向同正”的前提条件。
小结
主要内容
基本理论:
a - b > 0 <=> a > b
a - b = 0 <=> a = b
a - b < 0 <=> a < b
基本理论应用之一:比较实数的大小.
一般步骤:
作差-变形-判断符号-下结论
1°变形常用手段:配方法,因式分解法
2°变形常见形式是:变形为常数;
一个常数与几个平方和;几个因式的积
1.基本概念
同向不等式:
在两个不等式中,如果每一个的左边都大于右边,或每一个的左边都小于右边.
异向不等式:
在两个不等式中,如果一个不等式的左边大于右边,而另一个的左边小于右边.
作差比较两数大小的依据
上式中的左边反映的是实数的运算性质,而右边则是实数的大小顺序,合起来就成为实数的运算性质与大小顺序之间的关系。这一性质不仅可以用来比较两个实数的大小,而且是推导不等式的性质,不等式的证明,解不等式的主要依据。
判断两个实数a与b的大小,归结为判断它们的差a-b 的符号,从而归结为实数运算的符号法则,分三步进行:
作差比较两数大小的步骤
(1)作差;
(2)变形;
(3)定号;
(4)下结论;
常用手段:配方法,因式分
解法。
常见形式:变形为常数;
一个常数与几
个平方和;
几个因式的积。
作商比较两数大小的依据
若
例1:已知 ,那么在
这三个数中,最小的数是
____,最大的数是_______
解法1:
令
则
例1:已知 ,那么在
这三个数中,最小的数是
____,最大的数是_______
解法2:
化成若干因式相乘除来定号
化成若干因式相乘除来定号
