10.2一元二次不等式_课件-湘教版数学必修4(18张PPT)
文档属性
| 名称 | 10.2一元二次不等式_课件-湘教版数学必修4(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 639.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 09:15:40 | ||
图片预览





文档简介
一元二次不等式
复习一元二次方程
(1)公式法 X=
求根的方法:
(2)配方法,化为顶点式
(3)十字相乘法
复习一元二次方程:ax2+bx+c=0(a≠0)
方法一:
方法二:
方法三:
复习一元二次函数
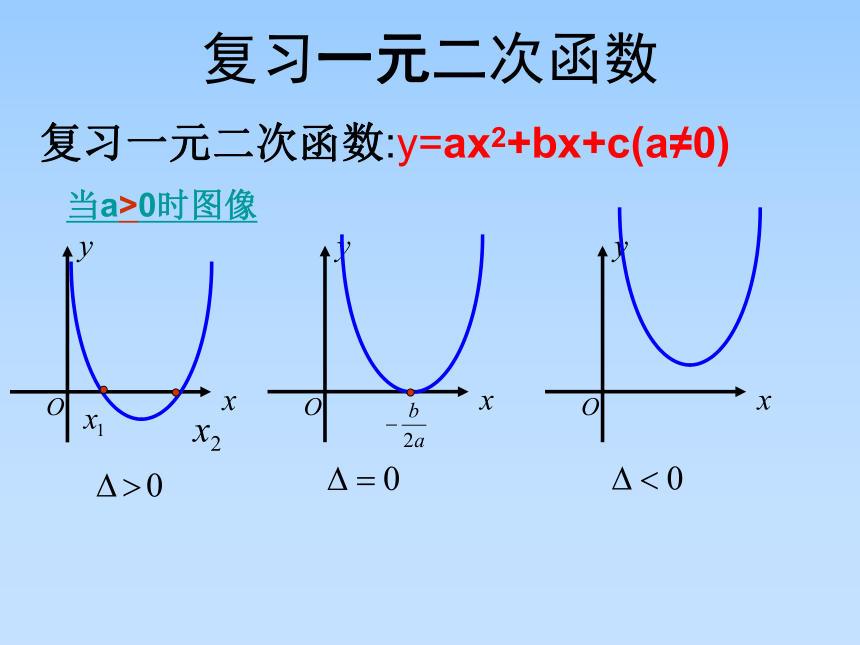
复习一元二次函数:y=ax2+bx+c(a≠0)
当a>0时图像
复习一元二次函数
复习一元二次函数:y=ax2+bx+c(a≠0)
当a<0时图像
是二次的不等式叫做一元二次不等式.
问题:如何解一元二次不等式呢?
定义:含有一个未知数,
并且未知数的最高次数
一元二次不等式定义:
形如: ax2+bx+c>0 或 ax2+bx+c<0(a≠0)
所以二次函数y=x2-2x-3的图象如图:
y
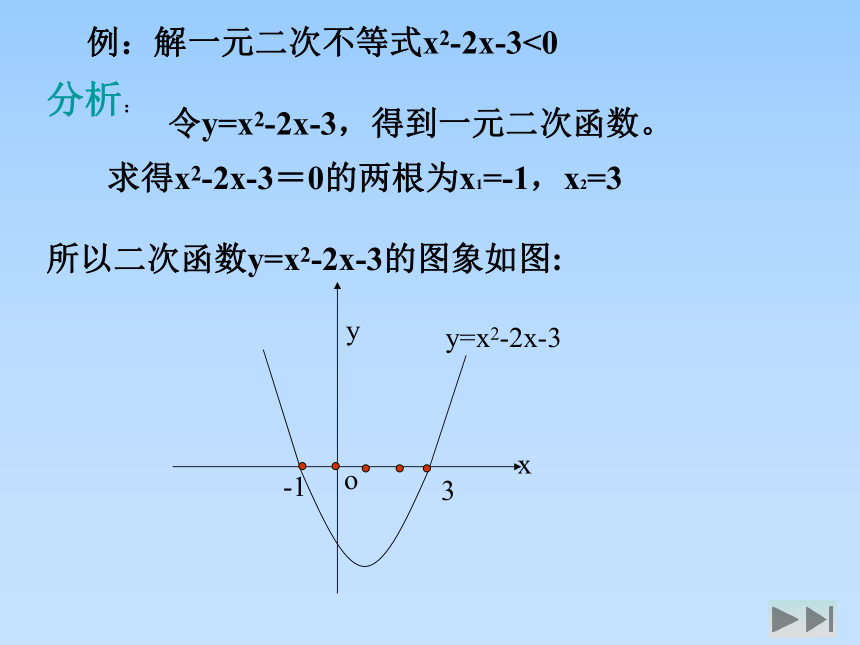
例:解一元二次不等式x2-2x-3<0
分析:
令y=x2-2x-3,得到一元二次函数。
求得x2-2x-3=0的两根为x1=-1,x2=3
y=x2-2x-3
x
o
-1
3
研究二次函数y=x2-2x-3的图象,图像如下:
(1).当x取 __________ 时,y=0?
当x取 __________ 时,y<0?
当x取 __________ 时,y>0?
x= -1 或3
x<-1 或 x>3
-1(2).由图象写出
不等式x2-2x-3 <0 的解集为
————————
不等式x2-2x-3<0 的解集为
————————
﹛x|x<-1或x>3﹜
﹛x|-1y
y=x2-2x-3
x
o
-1
3
y>0
y<0
问题探究:
归纳:
如何利用二次函数解二次不等式 呢?
(1)先画出对应函数的图像
(2)确定不等式的解集:
的解集就是确定函数
图像在X轴下方时,其x的取值范围
的解集就是确定函数
图像在X轴上方时,其x的取值范围
x1
x2
⊿=b2-4ac
二次函数 y=ax2+bx+c(a>0)
的图象
方程x2+bx+c=0
的根
ax2+bx+c>0(a>0)
的解集
ax2+bx+c<0 (a>0) 的解集
x1(x2)
⊿>0
⊿=0
⊿<0
有两个不等实根 x1,x2(x1﹛x|xx2﹜
﹛x|x1有两个相等实根x1=x2
无实根
﹛x|x≠x1﹜
Φ
Φ
R
一元二次不等式解集表(a>0)
y
x
x
y
x
y
例:解不等式:
例:解不等式:
例:解不等式:
例:解不等式:
例:解不等式:
例2:已知不等式 的解集是 ,求实数 的值.
典例精讲:
例:设A,B分别是不等式
与不等式 的解集,试求
解:
例:解关于x的不等式:
解:
含参变量
的不等式
例:解关于x的不等式:
解:
例:已知 恒成立,
求a的取值范围。
解:
不等式恒成立,即解集为R
小结
(1)不等式的解集的运算:注意利用数轴进行集合的交集和并集的运算
(2)含参变量的不等式问题:
注意区分自变量和参变量
注意比较两根的大小,利用分类讨论的数学思想
求参变量的取值问题,借助二次函数的图像,利用数形结合的数学思想
复习一元二次方程
(1)公式法 X=
求根的方法:
(2)配方法,化为顶点式
(3)十字相乘法
复习一元二次方程:ax2+bx+c=0(a≠0)
方法一:
方法二:
方法三:
复习一元二次函数
复习一元二次函数:y=ax2+bx+c(a≠0)
当a>0时图像
复习一元二次函数
复习一元二次函数:y=ax2+bx+c(a≠0)
当a<0时图像
是二次的不等式叫做一元二次不等式.
问题:如何解一元二次不等式呢?
定义:含有一个未知数,
并且未知数的最高次数
一元二次不等式定义:
形如: ax2+bx+c>0 或 ax2+bx+c<0(a≠0)
所以二次函数y=x2-2x-3的图象如图:
y
例:解一元二次不等式x2-2x-3<0
分析:
令y=x2-2x-3,得到一元二次函数。
求得x2-2x-3=0的两根为x1=-1,x2=3
y=x2-2x-3
x
o
-1
3
研究二次函数y=x2-2x-3的图象,图像如下:
(1).当x取 __________ 时,y=0?
当x取 __________ 时,y<0?
当x取 __________ 时,y>0?
x= -1 或3
x<-1 或 x>3
-1
不等式x2-2x-3 <0 的解集为
————————
不等式x2-2x-3<0 的解集为
————————
﹛x|x<-1或x>3﹜
﹛x|-1
y=x2-2x-3
x
o
-1
3
y>0
y<0
问题探究:
归纳:
如何利用二次函数解二次不等式 呢?
(1)先画出对应函数的图像
(2)确定不等式的解集:
的解集就是确定函数
图像在X轴下方时,其x的取值范围
的解集就是确定函数
图像在X轴上方时,其x的取值范围
x1
x2
⊿=b2-4ac
二次函数 y=ax2+bx+c(a>0)
的图象
方程x2+bx+c=0
的根
ax2+bx+c>0(a>0)
的解集
ax2+bx+c<0 (a>0) 的解集
x1(x2)
⊿>0
⊿=0
⊿<0
有两个不等实根 x1,x2(x1
﹛x|x1
无实根
﹛x|x≠x1﹜
Φ
Φ
R
一元二次不等式解集表(a>0)
y
x
x
y
x
y
例:解不等式:
例:解不等式:
例:解不等式:
例:解不等式:
例:解不等式:
例2:已知不等式 的解集是 ,求实数 的值.
典例精讲:
例:设A,B分别是不等式
与不等式 的解集,试求
解:
例:解关于x的不等式:
解:
含参变量
的不等式
例:解关于x的不等式:
解:
例:已知 恒成立,
求a的取值范围。
解:
不等式恒成立,即解集为R
小结
(1)不等式的解集的运算:注意利用数轴进行集合的交集和并集的运算
(2)含参变量的不等式问题:
注意区分自变量和参变量
注意比较两根的大小,利用分类讨论的数学思想
求参变量的取值问题,借助二次函数的图像,利用数形结合的数学思想
