2021-2022学年人教版九年级数学上册同步练习附答案:21.3 实际问题与一元二次方程
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册同步练习附答案:21.3 实际问题与一元二次方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 406.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览



文档简介
21.3
实际问题与一元二次方程
一、选择题(共6小题;共30分)
1.
在一幅长为
,宽为
的矩形中学生书画作品的四周镶一条相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个作品的面积是
,设金色纸边的宽为
,那么
满足的方程是
A.
B.
C.
D.
2.
关于
的方程的两根分别为
,,则这个方程可以为
A.
B.
C.
D.
3.
,
是一元二次方程
的两个根,,对
的估算正确的是
A.
B.
C.
D.
4.
要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排
天,每天安排
场比赛.设比赛组织者应邀请
个队参赛,则
满足的关系式为
A.
B.
C.
D.
5.
在一幅长
,宽
的风景画的四周的外边镶宽度相同的金色纸边,制成一幅挂图,使风景画的面积是整个挂图面积的
,设金色纸边的宽度为
,则可列方程为
A.
B.
C.
D.
6.
要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排
场比赛,则参赛球队的个数是
A.
个
B.
个
C.
个
D.
个
二、填空题(共3小题;共15分)
7.
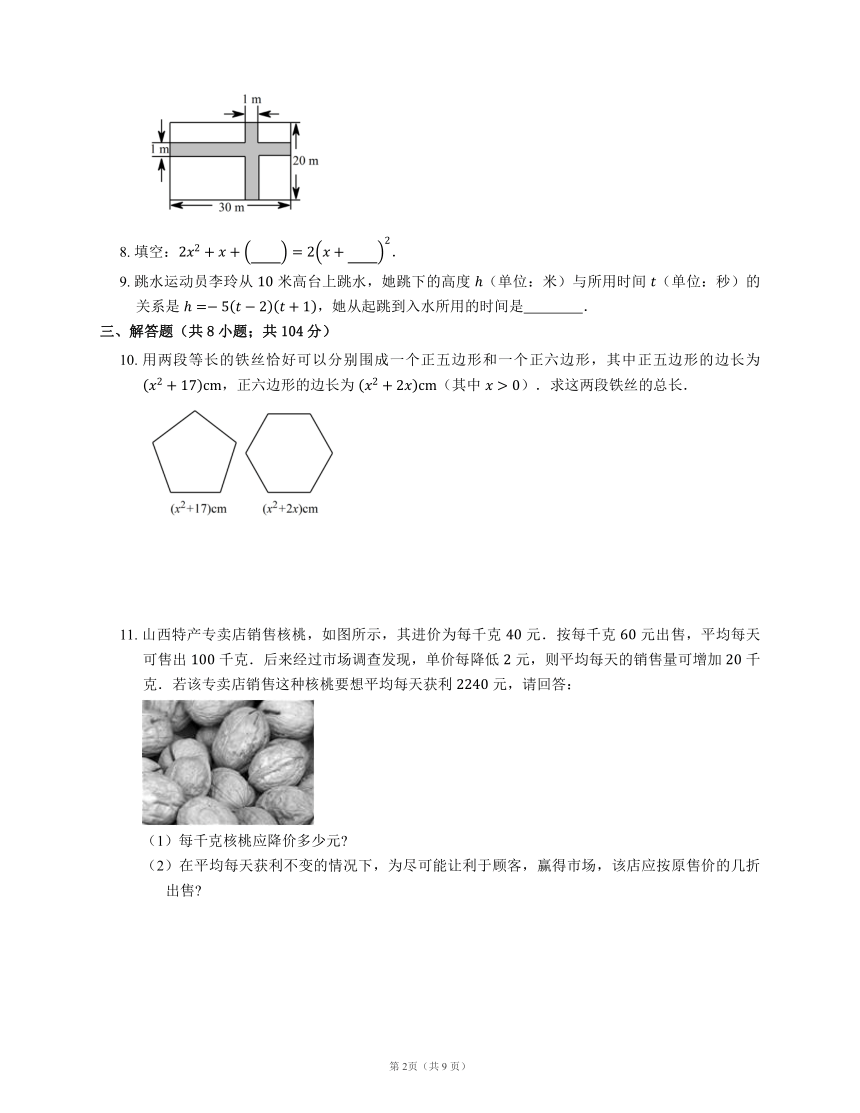
如图,在宽为
,长为
的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为
?.
8.
填空:.
9.
跳水运动员李玲从
米高台上跳水,她跳下的高度
(单位:米)与所用时间
(单位:秒)的关系是
,她从起跳到入水所用的时间是
?.
三、解答题(共8小题;共104分)
10.
用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为
,正六边形的边长为
(其中
).求这两段铁丝的总长.
11.
山西特产专卖店销售核桃,如图所示,其进价为每千克
元.按每千克
元出售,平均每天可售出
千克.后来经过市场调查发现,单价每降低
元,则平均每天的销售量可增加
千克.若该专卖店销售这种核桃要想平均每天获利
元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
12.
随着铁路运量的不断增长,重庆火车北站越来越拥挤,为了满足铁路交通的快速发展,该火车站从去年开始启动了扩建工程,其中某项工程,甲队单独完成所需时间比乙队单独完成所需时间多
个月,并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的
倍.
(1)求甲、乙队单独完成这项工程各需几个月?
(2)若甲队每月的施工费为
万元,乙队每月的施工费比甲队多
万元,在保证工程质量的前提下,为了缩短工期,拟安排甲、乙两队分工合作完成这项工程.在完成这项工程中,甲队施工时间是乙队施工时间的
倍,那么,甲队最多施工几个月才能使工程款不超过
万元?(甲、乙两队的施工时间按月取整数)
13.
为了倡导节能低碳的生活,某公司对集体宿舍用电作如下规定:一间宿舍一个月用电量若不超过
千瓦时,则一个月的电费为
元;若超过
千瓦时,则除了交
元外,超过部分每千瓦时要交
元.某宿舍
月份用电
千瓦时,交电费
元;
月份用电
千瓦时,交电费
元.
(1)求
的值;
(2)该宿舍
月份交电费为
元,那么该宿舍当月用电量为多少千瓦时?
14.
用长
的铁线围成一个面积为
的长方形,长和宽各为多少米?
15.
把一边长为
的正方形硬纸板进行适当的剪裁,折成一个长方形盒(纸板的厚度忽略不计).
(1)如图,若在正方形硬纸板的四角各剪掉一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子.要使折成的长方体盒子的底面积为
,那么剪掉的正方形的边长为多少?
折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分拆成一个有盖的长方体盒子,若折成的一个长方体盒子的表面积为
,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
16.
某校为培养青少年科技创新能力,举办了动漫制作活动,思思设计了点做圆周运动的一个雏型.如图所示,甲、乙两点分别从直径的两端点
,
以顺时针、逆时针的方向同时沿圆周运动.甲运动的路程
与时间
满足关系:,乙以
的速度匀速运动,半圆的长度为
.
(1)甲运动
后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
17.
低碳生活的理念已逐步被人们所接受.据相关资料统计:一个人平均一年节约的用电,相当于减排二氧化碳约
千克;一个人平均一年少买的衣服,相当于减排二氧化碳约
千克.
问题解决:
甲、乙两校分别对本校师生提出“节约用电”“少买衣服”的倡议.年两校响应本校倡议的人数共
人,因此而减排的二氧化碳总量为
千克.
(1)
年两校响应本校倡议的人数分别为多少?
(2)
年到
年,甲校响应本校倡议的人数每年增加相同的数量;乙校响应本校倡议的人数每年按相同的百分率增长.
年乙校响应本校倡议的人数是甲校响应本校倡议人数的
倍;
年两校响应本校倡议的总人数比
年两校响应本校倡议的总人数多
人.求
年两校因响应本校倡议减排二氧化碳的总量.
答案
1.
B
2.
D
3.
A
【解析】,
是一元二次方程
的两个根,
,
,
,
,
,
故选:A.
4.
B
5.
D
6.
C
【解析】设参赛球队有
个,
由题意得
,
解得
,(不合题意舍去),
故共有
个参赛球队.
7.
8.
,
9.
秒.
10.
由已知得,正五边形周长为
,
正六边形周长为
,
因为正五边形和正六边形的周长相等,
所以
.
整理得
,
解得
,(舍去),
故正五边形的周长为
.
又因为两段铁丝等长,
所以这两段铁丝的总长为
.
11.
(1)
设每千克核桃应降价
元.
根据题意,得
化简,得
解得
答:每千克核桃应降价
元或
元.
??????(2)
由(1)可知每千克核桃可降价
元或
元.
因为要尽可能让利于顾客,所以每千克核桃应降价
元.
此时,售价为
(元),.
答:该店应按原售价的九折出售.
12.
(1)
设甲队单独完成这项工程需要
个月,则乙队单独完成这项工程需要
个月.由题意,得
整理,得
解得
故
.
答:甲队单独完成这项工程需要
个月,则乙队单独完成这项工程需要
个月.
??????(2)
设在完成这项工程中甲队做了
个月,则乙队做了
个月.根据题意,得
解得
因为
为整数,所以
的最大值为
.
答:完成这项工程,甲队最多施工
个月.
13.
(1)
解得
因为
,
不合题意舍去.
所以
.
??????(2)
设宿舍
月份用电量为
千瓦时,
解得
答:该宿舍
月份用电量为
千瓦时.
14.
设长为
,则宽为
.
依题意得
所以长为
,宽为
.
15.
(1)
①设剪掉的正方形的边长为
,
则
解得
所以剪掉的正方形的边长为
.
②侧面积有最大值.
设剪掉的小正方形的边长为
,
盒子的侧面积为
,即
,
所以当
时,即当剪掉的正方形的边长为
时,长方形盒子的侧面积最大为
.
??????(2)
在如图的一种剪裁图中,设剪掉的小正方形的边长为
.
解得
所以剪掉的正方形的边长为
.
此时长方体盒子的长为
,宽为
,高为
.
16.
(1)
当
时,().
答:甲运动
后的路程是
.
??????(2)
设它们运动了
后第一次相遇,根据题意,得
解得
答:甲、乙从开始运动到第一次相遇时,它们运动了
.
??????(3)
设它们运动了
后第二次相遇,
.解得
答:甲、乙从开始运动到第二次相遇时,它们运动了
.
17.
(1)
设
年甲校响应本校倡议的人数为
人,乙校响应本校倡议的人数为
人.
依题意得
解得
所以
年甲、乙两校应倡议的人数分别是
人和
人.
??????(2)
设
年到
年,甲校响应本校倡议的人数每年增加
人;乙校响应本校倡议的人数每年增长的百分率为
.
依题意得
由①得
代入②并整理得
解之得
所以
,
所以
年两校响应本校倡议减排二氧化碳的总量:(千克).
答:
年两校响应本校倡议减排二氧化碳的总量为
千克.
第1页(共9
页)
实际问题与一元二次方程
一、选择题(共6小题;共30分)
1.
在一幅长为
,宽为
的矩形中学生书画作品的四周镶一条相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个作品的面积是
,设金色纸边的宽为
,那么
满足的方程是
A.
B.
C.
D.
2.
关于
的方程的两根分别为
,,则这个方程可以为
A.
B.
C.
D.
3.
,
是一元二次方程
的两个根,,对
的估算正确的是
A.
B.
C.
D.
4.
要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排
天,每天安排
场比赛.设比赛组织者应邀请
个队参赛,则
满足的关系式为
A.
B.
C.
D.
5.
在一幅长
,宽
的风景画的四周的外边镶宽度相同的金色纸边,制成一幅挂图,使风景画的面积是整个挂图面积的
,设金色纸边的宽度为
,则可列方程为
A.
B.
C.
D.
6.
要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排
场比赛,则参赛球队的个数是
A.
个
B.
个
C.
个
D.
个
二、填空题(共3小题;共15分)
7.
如图,在宽为
,长为
的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为
?.
8.
填空:.
9.
跳水运动员李玲从
米高台上跳水,她跳下的高度
(单位:米)与所用时间
(单位:秒)的关系是
,她从起跳到入水所用的时间是
?.
三、解答题(共8小题;共104分)
10.
用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为
,正六边形的边长为
(其中
).求这两段铁丝的总长.
11.
山西特产专卖店销售核桃,如图所示,其进价为每千克
元.按每千克
元出售,平均每天可售出
千克.后来经过市场调查发现,单价每降低
元,则平均每天的销售量可增加
千克.若该专卖店销售这种核桃要想平均每天获利
元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
12.
随着铁路运量的不断增长,重庆火车北站越来越拥挤,为了满足铁路交通的快速发展,该火车站从去年开始启动了扩建工程,其中某项工程,甲队单独完成所需时间比乙队单独完成所需时间多
个月,并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的
倍.
(1)求甲、乙队单独完成这项工程各需几个月?
(2)若甲队每月的施工费为
万元,乙队每月的施工费比甲队多
万元,在保证工程质量的前提下,为了缩短工期,拟安排甲、乙两队分工合作完成这项工程.在完成这项工程中,甲队施工时间是乙队施工时间的
倍,那么,甲队最多施工几个月才能使工程款不超过
万元?(甲、乙两队的施工时间按月取整数)
13.
为了倡导节能低碳的生活,某公司对集体宿舍用电作如下规定:一间宿舍一个月用电量若不超过
千瓦时,则一个月的电费为
元;若超过
千瓦时,则除了交
元外,超过部分每千瓦时要交
元.某宿舍
月份用电
千瓦时,交电费
元;
月份用电
千瓦时,交电费
元.
(1)求
的值;
(2)该宿舍
月份交电费为
元,那么该宿舍当月用电量为多少千瓦时?
14.
用长
的铁线围成一个面积为
的长方形,长和宽各为多少米?
15.
把一边长为
的正方形硬纸板进行适当的剪裁,折成一个长方形盒(纸板的厚度忽略不计).
(1)如图,若在正方形硬纸板的四角各剪掉一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子.要使折成的长方体盒子的底面积为
,那么剪掉的正方形的边长为多少?
折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分拆成一个有盖的长方体盒子,若折成的一个长方体盒子的表面积为
,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
16.
某校为培养青少年科技创新能力,举办了动漫制作活动,思思设计了点做圆周运动的一个雏型.如图所示,甲、乙两点分别从直径的两端点
,
以顺时针、逆时针的方向同时沿圆周运动.甲运动的路程
与时间
满足关系:,乙以
的速度匀速运动,半圆的长度为
.
(1)甲运动
后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
17.
低碳生活的理念已逐步被人们所接受.据相关资料统计:一个人平均一年节约的用电,相当于减排二氧化碳约
千克;一个人平均一年少买的衣服,相当于减排二氧化碳约
千克.
问题解决:
甲、乙两校分别对本校师生提出“节约用电”“少买衣服”的倡议.年两校响应本校倡议的人数共
人,因此而减排的二氧化碳总量为
千克.
(1)
年两校响应本校倡议的人数分别为多少?
(2)
年到
年,甲校响应本校倡议的人数每年增加相同的数量;乙校响应本校倡议的人数每年按相同的百分率增长.
年乙校响应本校倡议的人数是甲校响应本校倡议人数的
倍;
年两校响应本校倡议的总人数比
年两校响应本校倡议的总人数多
人.求
年两校因响应本校倡议减排二氧化碳的总量.
答案
1.
B
2.
D
3.
A
【解析】,
是一元二次方程
的两个根,
,
,
,
,
,
故选:A.
4.
B
5.
D
6.
C
【解析】设参赛球队有
个,
由题意得
,
解得
,(不合题意舍去),
故共有
个参赛球队.
7.
8.
,
9.
秒.
10.
由已知得,正五边形周长为
,
正六边形周长为
,
因为正五边形和正六边形的周长相等,
所以
.
整理得
,
解得
,(舍去),
故正五边形的周长为
.
又因为两段铁丝等长,
所以这两段铁丝的总长为
.
11.
(1)
设每千克核桃应降价
元.
根据题意,得
化简,得
解得
答:每千克核桃应降价
元或
元.
??????(2)
由(1)可知每千克核桃可降价
元或
元.
因为要尽可能让利于顾客,所以每千克核桃应降价
元.
此时,售价为
(元),.
答:该店应按原售价的九折出售.
12.
(1)
设甲队单独完成这项工程需要
个月,则乙队单独完成这项工程需要
个月.由题意,得
整理,得
解得
故
.
答:甲队单独完成这项工程需要
个月,则乙队单独完成这项工程需要
个月.
??????(2)
设在完成这项工程中甲队做了
个月,则乙队做了
个月.根据题意,得
解得
因为
为整数,所以
的最大值为
.
答:完成这项工程,甲队最多施工
个月.
13.
(1)
解得
因为
,
不合题意舍去.
所以
.
??????(2)
设宿舍
月份用电量为
千瓦时,
解得
答:该宿舍
月份用电量为
千瓦时.
14.
设长为
,则宽为
.
依题意得
所以长为
,宽为
.
15.
(1)
①设剪掉的正方形的边长为
,
则
解得
所以剪掉的正方形的边长为
.
②侧面积有最大值.
设剪掉的小正方形的边长为
,
盒子的侧面积为
,即
,
所以当
时,即当剪掉的正方形的边长为
时,长方形盒子的侧面积最大为
.
??????(2)
在如图的一种剪裁图中,设剪掉的小正方形的边长为
.
解得
所以剪掉的正方形的边长为
.
此时长方体盒子的长为
,宽为
,高为
.
16.
(1)
当
时,().
答:甲运动
后的路程是
.
??????(2)
设它们运动了
后第一次相遇,根据题意,得
解得
答:甲、乙从开始运动到第一次相遇时,它们运动了
.
??????(3)
设它们运动了
后第二次相遇,
.解得
答:甲、乙从开始运动到第二次相遇时,它们运动了
.
17.
(1)
设
年甲校响应本校倡议的人数为
人,乙校响应本校倡议的人数为
人.
依题意得
解得
所以
年甲、乙两校应倡议的人数分别是
人和
人.
??????(2)
设
年到
年,甲校响应本校倡议的人数每年增加
人;乙校响应本校倡议的人数每年增长的百分率为
.
依题意得
由①得
代入②并整理得
解之得
所以
,
所以
年两校响应本校倡议减排二氧化碳的总量:(千克).
答:
年两校响应本校倡议减排二氧化碳的总量为
千克.
第1页(共9
页)
同课章节目录
