2.5 三角函数的应用 课件(共25张PPT)
文档属性
| 名称 | 2.5 三角函数的应用 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 13:38:40 | ||
图片预览





文档简介
(共25张PPT)
第二章
直角三角形的边角关系
5
三角函数的应用
知识点一
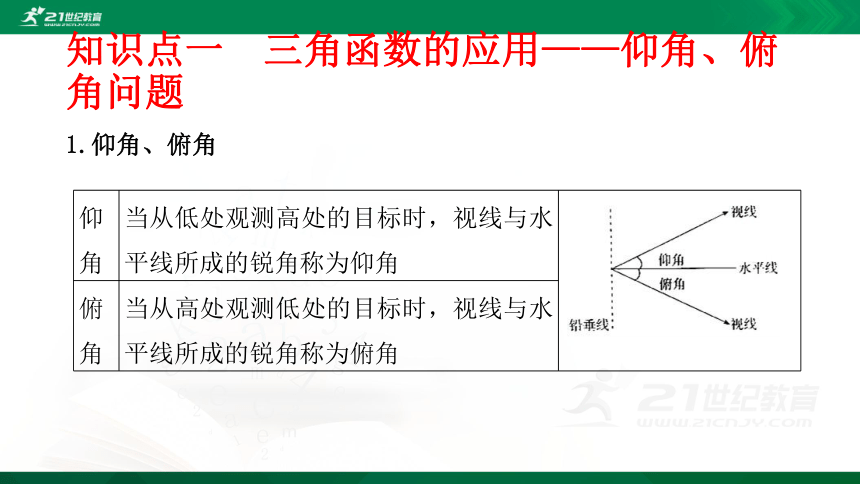
三角函数的应用——仰角、俯角问题
1.仰角、俯角
仰角
当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角
?
俯角
当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角
知识点一
三角函数的应用——仰角、俯角问题
2.三角函数的应用利用三角函数解决实际问题时,一般思路:从实际问题中抽象出数学问题,再将数学问题转化为解直角三角形问题.一般步骤如下所示转化:
在实际问题中应用解直角三角形的知识时,应先判断问题的类型,再根据类型选择相应的方法问题的类型一般分为以下两种:
(1)单直角三角形型若实际问题中可以找到可直接求解的直角三角形,或可构造可直接求解的直角三角形,便可以应用解直角三角形的知识直接求解.
(2)双直角三角形型这种类型又可以分为两种情况:
①实际问题中可找到或可构造两个直角三角形,其中一个直角三角形可直接求解,另一个直角三角形需在解第一个直角三角形的基础上求解.
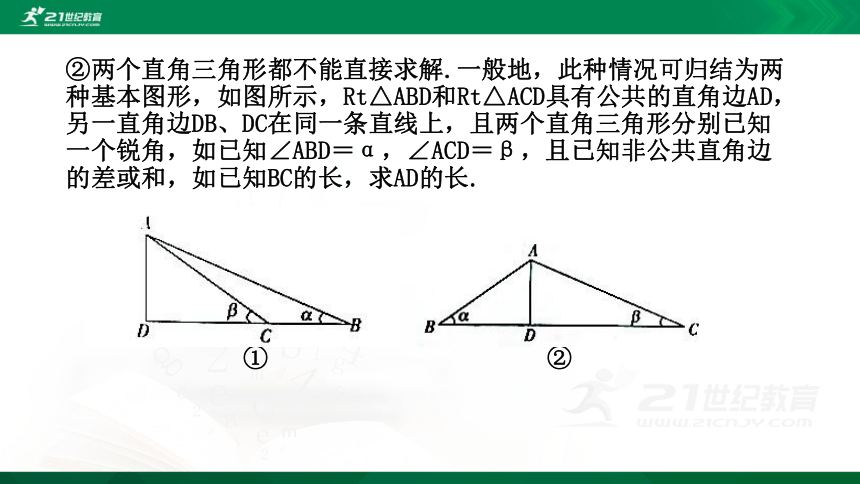
②两个直角三角形都不能直接求解.一般地,此种情况可归结为两种基本图形,如图所示,Rt△ABD和Rt△ACD具有公共的直角边AD,另一直角边DB、DC在同一条直线上,且两个直角三角形分别已知一个锐角,如已知∠ABD=α,∠ACD=β,且已知非公共直角边的差或和,如已知BC的长,求AD的长.
①
②
变式拓展
其他不能直接求解的双直角三角形可通过上下或左右平移转化为上面的两种基本图形,而其解决的方法也更灵活,通常是添加辅助线构造矩形与直角三角形,设某未知线段,并利用锐角三角函数或线段的和差关系表示其他未知线段,进而利用线段的和差关系或锐角三角函数列方程(组)解决问题.
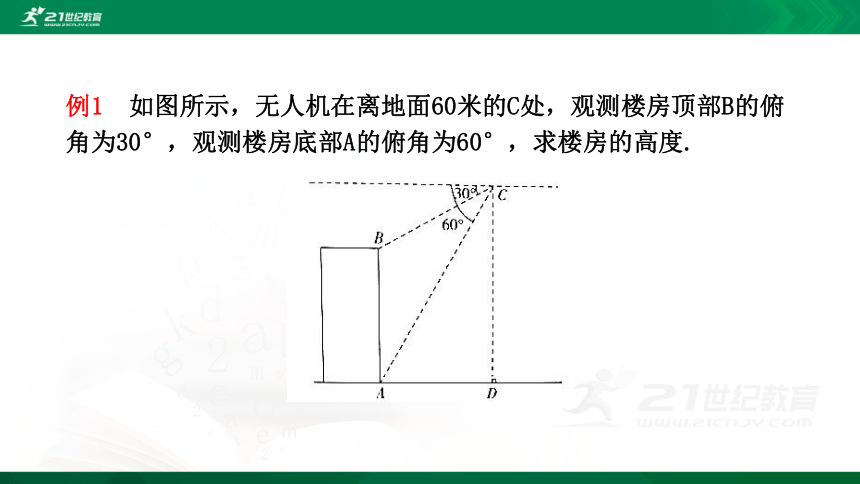
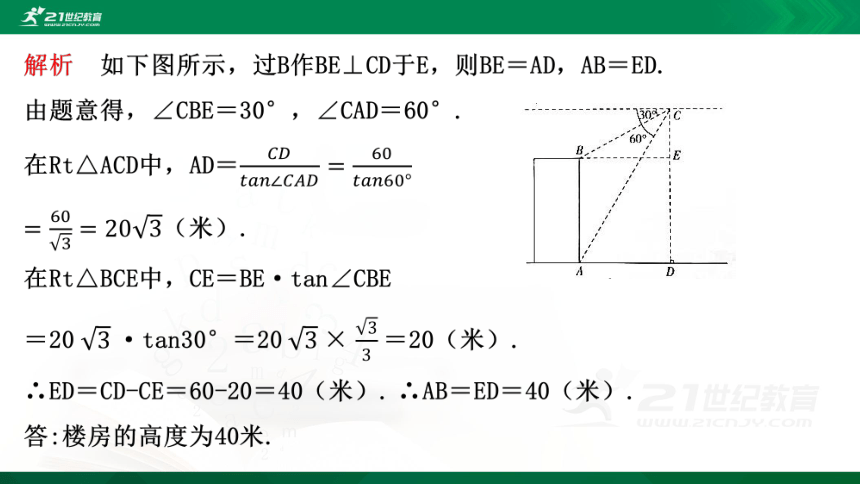
例1
如图所示,无人机在离地面60米的C处,观测楼房顶部B的俯角为30°,观测楼房底部A的俯角为60°,求楼房的高度.
知识点二
三角函数的应用——方向角问题
?
方向角
定义
以观察点为中心(方向角的顶点),正北或正南为始边,旋转到目标方向线所成的锐角称为方向角
解读
①方向角通常以南北方向线为主,分南偏和北偏,即“南偏东”“南偏西”“北偏东”“北偏西”一般不表示为“东偏……”或“西偏……”,例:如图所示,目标方向OD表示的方向角为北偏西40°,目标方向OB表示的方向角为南偏东45°;②观测点不同,所得的方向角不同(如图所示,从点O观测点C的方向角为南偏西35°,从点C观测点O的方向角为北偏东35°),各个观测点的南北方向线是互相平行的
?
提示
①“西北”指北偏西45°;②“西南”指南偏西45°;③“东北”指北偏东45°;④“东南”指南偏东45°
方法归纳
此题是典型的间接解双直角三角形问题.图形中两直角三角形都不能直接求解,但两直角三角形有公共直角边,另一直角边的差已知,因此可用公共直角边分别表示另一直角边,利用它们的差已知列方程,从而求出公共直角边的长,进而解决问题.
知识点三
三角函数的应用——坡度、坡角问题
例3
如图所示,某校教学楼后面紧邻着一个山坡,坡上面是一块平地,BC∥AD,BE⊥AD,斜坡AB长26
m,斜坡AB的坡比为12:5为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移________m时,才能确保山体不滑坡.(取tan50°=1.2)
方法归纳
坡度、坡角问题,通常添加辅助线,构造直角三角形与矩形,从而利用矩形的性质及解直角三角形的知识解决问题.
经典例题
题型一
方向角(定位)问题
例1
如图所示,一艘船由A港沿北偏东65°方向航行38km至B港,然后再沿北偏西42°方向航行至C港,已知C港在A港北偏东20°方向.
(1)直接写出∠C的度数;(2)求A,C两港之间的距离.(结果用含非特殊角的三角函数及根式表示即可)
方法归纳
添加辅助线,构造直角三角形是解答此类题的关键.添加辅助线时,注意构造含特殊角的直角三角形,以使问题简捷易解此外,涉及方向角问题,要注意找到基准点在基准点处画出表示方向(上北下南,左西右东)的十字形图案,分清四个方向,再画出正确的路线图.
题型二
仰角、俯角与坡度、坡角综合问题
例2
如图所示,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.
方法技巧
利用解直角三角形的知识解决实际问题通常用到两个技巧:一是添加辅助线,构造直角三角形;二是将某未知线段设为未知数,并利用锐角三角函数或等量关系表示其他相关线段,进而利用等量关系或锐角三角函数列方程解决问题.
第二章
直角三角形的边角关系
5
三角函数的应用
知识点一
三角函数的应用——仰角、俯角问题
1.仰角、俯角
仰角
当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角
?
俯角
当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角
知识点一
三角函数的应用——仰角、俯角问题
2.三角函数的应用利用三角函数解决实际问题时,一般思路:从实际问题中抽象出数学问题,再将数学问题转化为解直角三角形问题.一般步骤如下所示转化:
在实际问题中应用解直角三角形的知识时,应先判断问题的类型,再根据类型选择相应的方法问题的类型一般分为以下两种:
(1)单直角三角形型若实际问题中可以找到可直接求解的直角三角形,或可构造可直接求解的直角三角形,便可以应用解直角三角形的知识直接求解.
(2)双直角三角形型这种类型又可以分为两种情况:
①实际问题中可找到或可构造两个直角三角形,其中一个直角三角形可直接求解,另一个直角三角形需在解第一个直角三角形的基础上求解.
②两个直角三角形都不能直接求解.一般地,此种情况可归结为两种基本图形,如图所示,Rt△ABD和Rt△ACD具有公共的直角边AD,另一直角边DB、DC在同一条直线上,且两个直角三角形分别已知一个锐角,如已知∠ABD=α,∠ACD=β,且已知非公共直角边的差或和,如已知BC的长,求AD的长.
①
②
变式拓展
其他不能直接求解的双直角三角形可通过上下或左右平移转化为上面的两种基本图形,而其解决的方法也更灵活,通常是添加辅助线构造矩形与直角三角形,设某未知线段,并利用锐角三角函数或线段的和差关系表示其他未知线段,进而利用线段的和差关系或锐角三角函数列方程(组)解决问题.
例1
如图所示,无人机在离地面60米的C处,观测楼房顶部B的俯角为30°,观测楼房底部A的俯角为60°,求楼房的高度.
知识点二
三角函数的应用——方向角问题
?
方向角
定义
以观察点为中心(方向角的顶点),正北或正南为始边,旋转到目标方向线所成的锐角称为方向角
解读
①方向角通常以南北方向线为主,分南偏和北偏,即“南偏东”“南偏西”“北偏东”“北偏西”一般不表示为“东偏……”或“西偏……”,例:如图所示,目标方向OD表示的方向角为北偏西40°,目标方向OB表示的方向角为南偏东45°;②观测点不同,所得的方向角不同(如图所示,从点O观测点C的方向角为南偏西35°,从点C观测点O的方向角为北偏东35°),各个观测点的南北方向线是互相平行的
?
提示
①“西北”指北偏西45°;②“西南”指南偏西45°;③“东北”指北偏东45°;④“东南”指南偏东45°
方法归纳
此题是典型的间接解双直角三角形问题.图形中两直角三角形都不能直接求解,但两直角三角形有公共直角边,另一直角边的差已知,因此可用公共直角边分别表示另一直角边,利用它们的差已知列方程,从而求出公共直角边的长,进而解决问题.
知识点三
三角函数的应用——坡度、坡角问题
例3
如图所示,某校教学楼后面紧邻着一个山坡,坡上面是一块平地,BC∥AD,BE⊥AD,斜坡AB长26
m,斜坡AB的坡比为12:5为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移________m时,才能确保山体不滑坡.(取tan50°=1.2)
方法归纳
坡度、坡角问题,通常添加辅助线,构造直角三角形与矩形,从而利用矩形的性质及解直角三角形的知识解决问题.
经典例题
题型一
方向角(定位)问题
例1
如图所示,一艘船由A港沿北偏东65°方向航行38km至B港,然后再沿北偏西42°方向航行至C港,已知C港在A港北偏东20°方向.
(1)直接写出∠C的度数;(2)求A,C两港之间的距离.(结果用含非特殊角的三角函数及根式表示即可)
方法归纳
添加辅助线,构造直角三角形是解答此类题的关键.添加辅助线时,注意构造含特殊角的直角三角形,以使问题简捷易解此外,涉及方向角问题,要注意找到基准点在基准点处画出表示方向(上北下南,左西右东)的十字形图案,分清四个方向,再画出正确的路线图.
题型二
仰角、俯角与坡度、坡角综合问题
例2
如图所示,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.
方法技巧
利用解直角三角形的知识解决实际问题通常用到两个技巧:一是添加辅助线,构造直角三角形;二是将某未知线段设为未知数,并利用锐角三角函数或等量关系表示其他相关线段,进而利用等量关系或锐角三角函数列方程解决问题.
