2021-2022学年人教版版数学九年级上册22.1.3.1 二次函数y=ax?+k的图象和性质导学案
文档属性
| 名称 | 2021-2022学年人教版版数学九年级上册22.1.3.1 二次函数y=ax?+k的图象和性质导学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 120.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览


文档简介
22.1.3.1
二次函数y=ax?+k的图象和性质导学案
学习目标:
1.会画二次函数y=ax
?
+k的图象.
2.掌握二次函数y=ax
?
+k的性质并会应用.
3.比较函数y=ax
?与y=ax
?+k的联系.
学习重难点:
重点:会画二次函数y=ax
?
+k的图象.
难点:掌握二次函数y=ax
?
+k的性质并会应用.
一、复习回顾
二次函数y=ax
?的图象是什么形状呢?什么确定y=ax
?的性质?通常怎样画一个函数的图象?
二、情境导入
你能在同一坐标系中,画出二次函数y=
x
?+1,y=x
?-1的图像吗?知道它们的开口方向、对称轴和顶点吗?
三、知识讲解
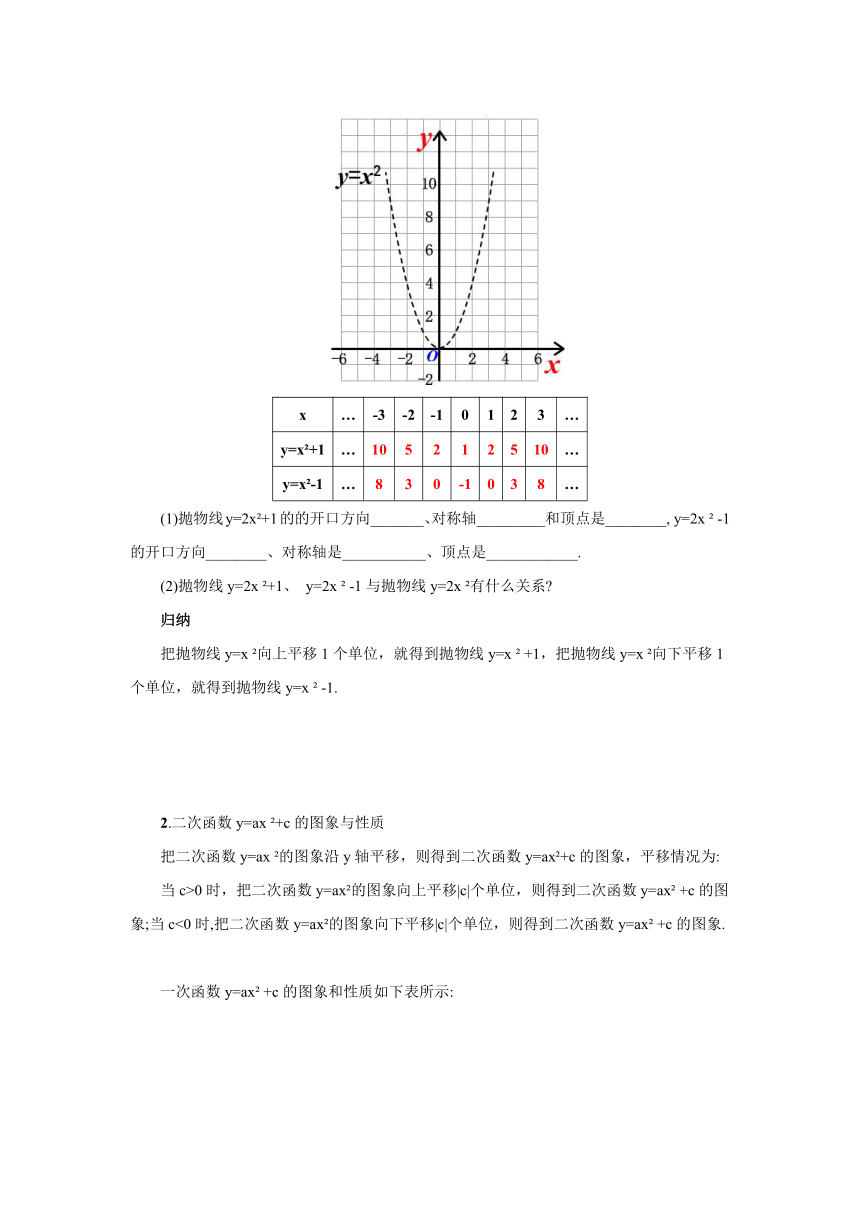
1.在同一坐标系下作出y=x?+1与y=x?-1的图象
x
…
-3
-2
-1
0
1
2
3
…
y=x?+1
…
10
5
2
1
2
5
10
…
y=x?-1
…
8
3
0
-1
0
3
8
…
(1)抛物线y=2x?+1的的开口方向_______、对称轴_________和顶点是________,
y=2x
?
-1的开口方向________、对称轴是___________、顶点是____________.
(2)抛物线y=2x
?+1、
y=2x
?
-1与抛物线y=2x
?有什么关系?
归纳
把抛物线y=x
?向上平移1个单位,就得到抛物线y=x
?
+1,把抛物线y=x
?向下平移1个单位,就得到抛物线y=x
?
-1.
2.二次函数y=ax
?+c的图象与性质
把二次函数y=ax
?的图象沿y轴平移,则得到二次函数y=ax?+c的图象,平移情况为:
当c>0时,把二次函数y=ax?的图象向上平移|c|个单位,则得到二次函数y=ax?
+c的图象;当c<0时,把二次函数y=ax?的图象向下平移|c|个单位,则得到二次函数y=ax?
+c的图象.
一次函数y=ax?
+c的图象和性质如下表所示:
四、例题精讲
1.y=ax?+c的图形与性质
例1
已知函数:y=-?x?、y=-?x?+3和y=-?x?-1.
(1)分别画出它们的图象;
(2)说出各个图象的开口方向,对称轴的顶点坐标;
(3)说出函数y=-?x?+6.的图象的开口方向、对称轴和顶点坐标;
(4)试说明函数y=-?x?+3、y=-?x?-1、y=-?x?+6的图象分别由抛物线y=-?x?作怎样的平移才能得到.
解:(1)如图所示:
(2)
y=-?x?开口向下,对称轴为y轴,顶点坐标为(0,0),
y=-?x?+3开口向下,对称轴为y轴,顶点坐标为(0,3),
y=-?x?-1开口向下,对称轴为y轴,顶点坐标为(0,-1);
(3)
y=-?x?+6的图象的开口向下,对称轴为y轴,顶点坐标为(0,6);
(4)
y=-?x?+3由抛物线y=-?x?向上平移3个单位,
y=-?x?-1由抛物线y=-?x?向下平移1个单位,
y=-?x?+6由抛物线y=-?x?向上平移6个单位.
归纳
注意数形结合思想的应用,根据函数图象直接作答.
变式训练:
如图.已知二次函数y=-
?x
?+2的图像与x.y轴分别交于点A、B、C.
(1)直接写出抛物线的顶点坐标.对称轴;
(2)若y随x的增大而减小,求x的取值范围;
(3)求?ABC的面积.
2.函数与几何
例2
已知抛物线y=?
x?
+1(如图所示)。
(1)填空:抛物线的顶点坐标是(___,____),对称轴是_____?。
(2)已知轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若?
PAB是等边三角形,求点P的坐标。
解:(1)(0,1);y轴(或x=0).
(2)如图所示,∵?
PAB是等边三角形,
∴∠ABO=90°-60°=30°,
∴AB=2OA=2×2=4,
∴PB=AB=4,将y=4代入二次函数y=?
x?
+1,得x?=12,
解得x=±2√,
∴P的坐标为(2√,4)或(-2√,4).
归纳
利用函数y=ax?+c的图象与性质直接写出顶点坐标和对称轴即可,根据等边三角形的性质求得PB=4,将PB=4代入函数的解析式后求得x的值即可作为P点的横坐标,代入解析式即可求得P点的纵坐标.
变式训练
如图,已知二次函数y=ax?+1(a≠0,a为实数)的图象过点A(-2,2),一次函数y=kx+b(k≠0,k、b为实数)的图象l经过点B(0,2).
(1)求a值并写出二次函数表达式;
(2)求b值;
(3)设直线l与二次函数图象交于M、N两点,过M作MC垂直⊥x轴于点C,试证明:MB=MC.
深入探究
如图,隧道的截图由抛物线和长方形构成,长方形的长是8
m,宽是2
m,抛物线可以用y=-x2+4表示.一辆货运卡车高4
m,宽2
m,它能通过该隧道吗?
我的收获
__________________________________________________________________________________________________________________________________________________________
二次函数y=ax?+k的图象和性质导学案
学习目标:
1.会画二次函数y=ax
?
+k的图象.
2.掌握二次函数y=ax
?
+k的性质并会应用.
3.比较函数y=ax
?与y=ax
?+k的联系.
学习重难点:
重点:会画二次函数y=ax
?
+k的图象.
难点:掌握二次函数y=ax
?
+k的性质并会应用.
一、复习回顾
二次函数y=ax
?的图象是什么形状呢?什么确定y=ax
?的性质?通常怎样画一个函数的图象?
二、情境导入
你能在同一坐标系中,画出二次函数y=
x
?+1,y=x
?-1的图像吗?知道它们的开口方向、对称轴和顶点吗?
三、知识讲解
1.在同一坐标系下作出y=x?+1与y=x?-1的图象
x
…
-3
-2
-1
0
1
2
3
…
y=x?+1
…
10
5
2
1
2
5
10
…
y=x?-1
…
8
3
0
-1
0
3
8
…
(1)抛物线y=2x?+1的的开口方向_______、对称轴_________和顶点是________,
y=2x
?
-1的开口方向________、对称轴是___________、顶点是____________.
(2)抛物线y=2x
?+1、
y=2x
?
-1与抛物线y=2x
?有什么关系?
归纳
把抛物线y=x
?向上平移1个单位,就得到抛物线y=x
?
+1,把抛物线y=x
?向下平移1个单位,就得到抛物线y=x
?
-1.
2.二次函数y=ax
?+c的图象与性质
把二次函数y=ax
?的图象沿y轴平移,则得到二次函数y=ax?+c的图象,平移情况为:
当c>0时,把二次函数y=ax?的图象向上平移|c|个单位,则得到二次函数y=ax?
+c的图象;当c<0时,把二次函数y=ax?的图象向下平移|c|个单位,则得到二次函数y=ax?
+c的图象.
一次函数y=ax?
+c的图象和性质如下表所示:
四、例题精讲
1.y=ax?+c的图形与性质
例1
已知函数:y=-?x?、y=-?x?+3和y=-?x?-1.
(1)分别画出它们的图象;
(2)说出各个图象的开口方向,对称轴的顶点坐标;
(3)说出函数y=-?x?+6.的图象的开口方向、对称轴和顶点坐标;
(4)试说明函数y=-?x?+3、y=-?x?-1、y=-?x?+6的图象分别由抛物线y=-?x?作怎样的平移才能得到.
解:(1)如图所示:
(2)
y=-?x?开口向下,对称轴为y轴,顶点坐标为(0,0),
y=-?x?+3开口向下,对称轴为y轴,顶点坐标为(0,3),
y=-?x?-1开口向下,对称轴为y轴,顶点坐标为(0,-1);
(3)
y=-?x?+6的图象的开口向下,对称轴为y轴,顶点坐标为(0,6);
(4)
y=-?x?+3由抛物线y=-?x?向上平移3个单位,
y=-?x?-1由抛物线y=-?x?向下平移1个单位,
y=-?x?+6由抛物线y=-?x?向上平移6个单位.
归纳
注意数形结合思想的应用,根据函数图象直接作答.
变式训练:
如图.已知二次函数y=-
?x
?+2的图像与x.y轴分别交于点A、B、C.
(1)直接写出抛物线的顶点坐标.对称轴;
(2)若y随x的增大而减小,求x的取值范围;
(3)求?ABC的面积.
2.函数与几何
例2
已知抛物线y=?
x?
+1(如图所示)。
(1)填空:抛物线的顶点坐标是(___,____),对称轴是_____?。
(2)已知轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若?
PAB是等边三角形,求点P的坐标。
解:(1)(0,1);y轴(或x=0).
(2)如图所示,∵?
PAB是等边三角形,
∴∠ABO=90°-60°=30°,
∴AB=2OA=2×2=4,
∴PB=AB=4,将y=4代入二次函数y=?
x?
+1,得x?=12,
解得x=±2√,
∴P的坐标为(2√,4)或(-2√,4).
归纳
利用函数y=ax?+c的图象与性质直接写出顶点坐标和对称轴即可,根据等边三角形的性质求得PB=4,将PB=4代入函数的解析式后求得x的值即可作为P点的横坐标,代入解析式即可求得P点的纵坐标.
变式训练
如图,已知二次函数y=ax?+1(a≠0,a为实数)的图象过点A(-2,2),一次函数y=kx+b(k≠0,k、b为实数)的图象l经过点B(0,2).
(1)求a值并写出二次函数表达式;
(2)求b值;
(3)设直线l与二次函数图象交于M、N两点,过M作MC垂直⊥x轴于点C,试证明:MB=MC.
深入探究
如图,隧道的截图由抛物线和长方形构成,长方形的长是8
m,宽是2
m,抛物线可以用y=-x2+4表示.一辆货运卡车高4
m,宽2
m,它能通过该隧道吗?
我的收获
__________________________________________________________________________________________________________________________________________________________
同课章节目录
