湖南省永州市零陵区2020-2021学年八年级下学期期末数学综合测试题(word版含解析)
文档属性
| 名称 | 湖南省永州市零陵区2020-2021学年八年级下学期期末数学综合测试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 371.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 14:31:12 | ||
图片预览




文档简介
2020-2021学年八年级(下)期末数学综合测试题
一.选择题(共10小题,满分40分,每小题4分)
1.下列条件中,使△ABC不是直角三角形的是( )
A.a=3,b=4,c=5
B.a2+b2=c2
C.a:b:c=2:2:3
D.∠A:∠B:∠C=1:2:3
2.下列图案中是中心对称图形但不是轴对称图形的是( )
A.
B.
C.
D.
3.“新冠病毒”的英语“Novelcoronavirus”中,字母“n”出现的频率是( )
A.
B.
C.2
D.1
4.如图,在平行四边形ABCD中,若点E是BD的中点,点M是AD上一动点,连接MB,MC,ME,并延长ME交BC于点N,设MD=tAM,有以下结论:①当t=1时,则BM=CM;②当t=2时,则S△MNC=S△EBM;③若△ABM≌△NMC,则MN⊥BD.其中正确的是( )
A.①
B.②
C.③
D.②③
5.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD
B.∠ABD=∠CBD
C.AB=BC
D.AC=BD
6.在同一直角坐标系中,一次函数y=kx+b和y=bx+k的图象可能正确的是( )
A.
B.
C.
D.
7.点P1(x1,y1),点P2(x2,y2)是一次函数y=﹣4x+3图象上的两个点,且x1>x2,则y1与y2的大小关系是( )
A.y1<y2
B.y1>y2
C.y1>y2>0
D.y1=y2
8.如图,∠MON=60°,OA平分∠MON,P是射线OA上的一点,且OP=4,若点Q是射线OM上的一个动点,则PQ的最小值为( )
A.1
B.2
C.3
D.4
9.如图,在矩形ABCD中,AB=m,BC=6,点E在边CD上,且CE=m.连接BE,将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,则m=( )
A.3
B.2
C.
D.5
10.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t=或t=,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,满分32分,每小题4分)
11.函数y=中,自变量x的取值范围是
.
12.已知一个n边形的内角和等于1980°,则n=
.
13.有人做过掷硬币的实验,掷一枚一元硬币4040次,结果正面(有国徽的一面)向上的次数为2048次,则正面向上的频率是
(保留两位有效数字).
14.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是
.
15.已知一次函数y=2x+5,当﹣2≤x≤6时,y的最大值是
.
16.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、AD的中点,EF=3,则AB的长度为
.
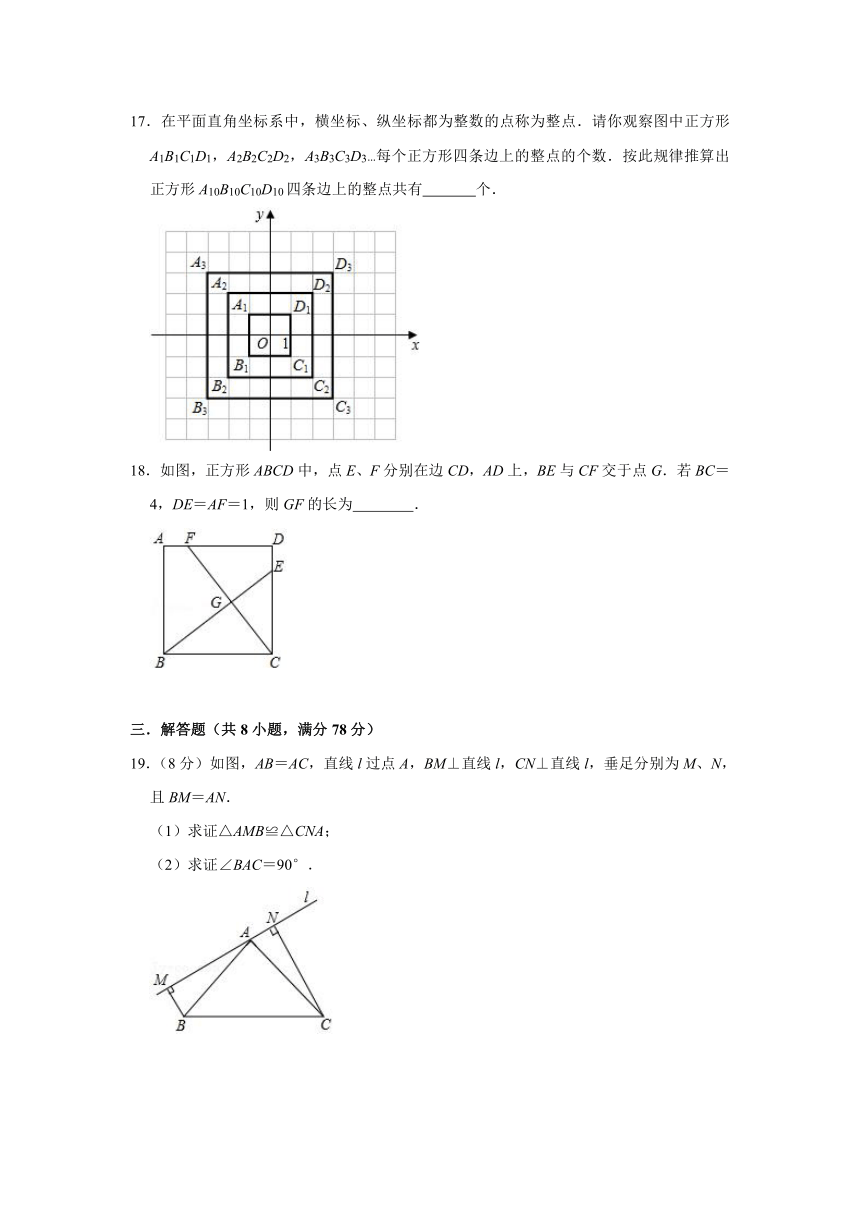
17.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有
个.
18.如图,正方形ABCD中,点E、F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为
.
三.解答题(共8小题,满分78分)
19.(8分)如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.
(1)求证△AMB≌△CNA;
(2)求证∠BAC=90°.
20.(8分)为了解某校七年级学生的跳高水平,随机抽取该年级60名学生进行跳高测试,并把测试成绩分成四组,绘制成如图所示的频数表和未完成的频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校七年级60名学生跳高测试成绩的频数表
组别(m)
频数
1.09~1.19
8
1.19~1.29
16
1.29~1.39
a
1.39~1.49
12
(1)求a的值;
(2)把频数分布直方图补充完整;
(3)求跳高成绩在1.29m(含1.29m)以上的学生数占参加测试学生数的百分比.
21.(8分)如图,在平面直角坐标系中,A(﹣5,3)、B(﹣4,4)、C(﹣3,2).
(1)将△ABC向下平移4个单位,再向右平移2个单位,画出平移后的图形△A1B1C1
(2)画出△ABC关于直线x=﹣1的对称图形△A2B2C2
(3)求△ABC的面积
S△ABC.
22.(10分)如图,在△ABC中,AB=AC,点E、F分别是BC、AC边上的中点,过点A作AD∥BC,交EF的延长线于点D
(1)求证:四边形ABED是平行四边形;
(2)若AB=4,∠BAC=120°,求四边形ABED的周长.
23.(10分)元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
24.(10分)如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AE=8,AB=4,求PE的长.
25.(12分)(1)如图1,在四边形ABCD中,∠B=∠C=90°,点E是边BC上一点,AB=EC,BE=CD,连接AE、DE,求证△AED是等腰直角三角形.
(2)如图2,一次函数y=﹣2x+2的图象与y轴交于点A,与x轴交于点B,直线AC交x轴于点D,且∠CAB=45°,则点D的坐标为
.
26.(12分)在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE.
(1)如图1,当点P在线段BD上时,连接CE,BP与CE的数量关系是
;CE与AD的位置关系是
;
(2)当点P在线段BD的延长线上时,(1)中的结论是否还成立?若成立,请予以证明,若不成立,请说明理由;(请结合图2的情况予以证明或说理)
(3)如图3,在(2)的条件下,连接BE,若AB=2,BE=,求四边形ADPE的面积.
参考答案
一.选择题(共10小题,满分40分,每小题4分)
1.解:A、∵32+42=52,∴△ABC是直角三角形,不符合题意;
B、∵a2+b2=c2,∴△ABC是直角三角形,不符合题意;
C、∵22+22≠32,∴△ABC不是直角三角形,符合题意;
D、∵∠A:∠B:∠C=1:2:3,∴∠C=90°,∴△ABC是直角三角形,不符合题意;
故选:C.
2.解:A、是中心对称图形,也是轴对称图形,不符合题意;
B、不是中心对称图形,是轴对称图形,不符合题意;
C、是中心对称图形,不是轴对称图形,符合题意;
D、不是轴对称图形,也不是中心对称图形,不符合题意.
故选:C.
3.解:在“Novelcoronavirus”中,字母的总数是16,字母“n”有2个,
因而字母“n”出现的频率是:=.
故选:B.
4.解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠BDA=∠DBC,
∵点E是BD的中点,
∴DE=BE,
在△DME和△BNE中,
,
∴△DME≌△BNE(ASA),
∴DM=BN,ME=NE,
∵t=1,
∴AM=DM=AD,
∴BN=BC=CN,
∴只有当MN⊥BC时,CM=BM,
∴①错误,
当t=2时,则DM=2AM,
∴BN=2CN,
∴S△BMN=2S△MNC,
∵ME=EN,
∴S△BEM=S△BMN,
∴S△BEM=S△MNC,
故②正确,
若△ABM≌△NMC,则BM=MC,当BM不一定等于BN,
∴MN⊥BD不一定成立,故③错误,
故选:B.
5.解:添加AC=BD,理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,
故选:D.
6.解:A、一条直线反映k>0,b>0,一条直线反映k>0,b<0,故本选项错误;
B、一条直线反映出k>0,b<0,一条直线反映k>0,b<0,一致,故本选项正确;
C、一条直线反映k<0,b>0,一条直线反映k>0,b<0,故本选项错误;
D、一条直线反映k>0,b<0,一条直线反映k<0,b<0,故本选项错误.
故选:B.
7.解:∵k=﹣4<0,
∴y随x的增大而减小,
又∵x1>x2,
∴y1<y2.
故选:A.
8.解:作PQ′⊥OM于Q′,
∵∠MON=60°,OP平分∠MON,
∴∠POQ′=30°,
∴PQ′=OP=2,
由垂线段最短可知,PQ的最小值是2,
故选:B.
9.解:∵四边形ABCD是矩形,
∴AD=BC=6,CD=AB=m,∠A=∠D=∠C=90°.
∵将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,
∴BC'=BC=6,∠BC'E=∠C=90°,C'E=CE=m,DE=CD﹣CE=m﹣m=m,
∴DE=C'E,
∴∠DC'E=30°,
∴∠AC'B=180°﹣90°﹣30°=60°,
∴AB=BC'×sin∠AC'B=6×=3,
即m=3;
故选:A.
10.解:由图象可知A、B两城市之间的距离为300km,故①正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
把y=150代入y甲=60t,可得:t=2.5,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(2.5,150)代入可得,
解得,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
乙的速度:150÷(2.5﹣1)=100,
乙的时间:300÷100=3,
甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故②正确;
甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③错误;
令|y甲﹣y乙|=40,可得|60t﹣100t+100|=40,即|100﹣40t|=40,
当100﹣40t=40时,可解得t=,
当100﹣40t=﹣40时,可解得t=,
又当t=时,y甲=40,此时乙还没出发,
当t=时,乙到达B城,y甲=260;
综上可知当t的值为或或或t=时,两车相距40千米,故④不正确;
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
11.解:根据题意,得:,
解得:x≤2且x≠﹣2,
故答案为:x≤2且x≠﹣2.
12.解:设这个多边形的边数为n,
则(n﹣2)?180°=1980°,
解得n=13.
故答案为:13.
13.解:掷一枚一元硬币4040次,结果正面(有国徽的一面)向上的次数为2048次,
则正面向上的频率是2048÷4040≈0.51.
14.解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,
∴1+m=3、1﹣n=2,
解得:m=2、n=﹣1,
所以m+n=2﹣1=1,
故答案为:1.
15.解:∵一次函数y=2x+5,
∴该函数的图象y随x的增大而增大,
∵﹣2≤x≤6,
∴当x=6时,y取得最大值,此时y=17,
故答案为:17.
16.解:∵E、F分别是AC、AD的中点,
∴AE=EC,AF=DF,
∴EF∥CD,CD=2EF,
∵EF=3,
∴CD=6,
∵∠ACB=90°,D是AB的中点,
∴AB=2CD=12,
故答案为12.
17.解:A1B1C1D1四条边上的整点共有8个,即4+4×1=8,
A2B2C2D2四条边上的整点共有16个,即4+4×3=16,
正方形A3B3C3D3四条边上的整点的个数有4+4×5=24,
…正方形A10B10C10D10四条边上的整点的个数有:4+4×19=80,
故答案为:80.
18.解:∵四边形ABCD为正方形,BC=4,
∴∠CDF=∠BCE=90°,AD=DC=BC=4,
又∵DE=AF=1,
∴CE=DF=3,
∴在△CDF和△BCE中,
,
∴△CDF≌△BCE(SAS),
∴∠DCF=∠CBE,
∵∠DCF+∠BCF=90°,
∴∠CBE+∠BCF=90°,
∴∠BGC=90°,
∵在Rt△BCE中,BC=4,CE=3,
∴BE=5,
∴BE?CG=BC?CE,
∴CG===,
∵△CDF≌△BCE(SAS),
∴CF=BE=5,
∴GF=CF﹣CG=5﹣=2.6.
故答案为:2.6.
三.解答题(共8小题,满分66分)
19.证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL);
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
20.解:(1)a=60﹣8﹣16﹣12=24(人),
答:a的值为24;
(2)补全频数分布直方图如下:
(3)×100%=60%,
答:跳高成绩在1.29m(含1.29m)以上的学生数占参加测试学生数的60%.
21.解:如图,添加网格结构,
(1)如图所示,△A1B1C1为所求作的三角形;
(2)△A2B2C2为所求作的三角形;
(3)S△ABC=2×2﹣×1×1﹣×1×2﹣×1×2=4﹣﹣1﹣1=1.5.
22.(1)证明:∵点E、F分别是BC、AC边上的中点
∴DE∥AB,
又AD∥BC,
∴四边形ABED是平行四边形;
(2)解:连接AE,
∵AB=AC,点E是BC边上的中点,
∴∠AEB=90°,∠BAE==60°,
∴∠ABE=30°,
∴在Rt△ABE中,,∴,
由(1)知,四边形ABED是平行四边形,
∴四边形ABED的周长=.
23.解:(1)设OA段图象的函数表达式为y=kx.
∵当x=0.8时,y=48,
∴0.8k=48,
∴k=60.
∴y=60x(0≤x≤0.8),
∴当x=0.5时,y=60×0.5=30.
故小黄出发0.5小时时,离家30千米;
(2)设AB段图象的函数表达式为y=k′x+b.
∵A(0.8,48),B(2,156)在AB上,
,
解得,
∴y=90x﹣24(0.8≤x≤2);
(3)∵当x=1.5时,y=90×1.5﹣24=111,
∴156﹣111=45.
故小黄出发1.5小时时,离目的地还有45千米.
24.(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵PB=PE,
∴四边形BPEQ是菱形;
(2)解:设PE=BP=x,则AP=8﹣x,
在Rt△ABP中,AP2+AB2=BP2,
即(8﹣x)2+42=x2,
解得x=5,
∴PE=5.
25.(1)证明:∵在△ABE和△ECD中,
,
∴△ABE≌△ECD
(SAS),
∴AE=DE,∠AEB=∠EDC,
在Rt△EDC中,∠C=90°,
∴∠EDC+∠DEC=90°.
∴∠AEB+∠DEC=90°.
∵∠AEB+∠DEC+∠AED=180°,
∴∠AED=90°.
∴△AED是等腰直角三角形;
(2)解:如图2,过点B作BE⊥AB,交AD于点E,过点E作EF⊥OD,交OD于点F,
把x=0代入y=﹣2x+2中,得y=2,
∴点A的坐标为(0,2),
∴OA=2,
把y=0代入y=﹣2x+2,得﹣2x+2=0,解得x=1,
∴点B的坐标为(1,0),
∴OB=1,
∵AO⊥OB,EF⊥BD,
∴∠AOB=∠BFE=90°,
∵AB⊥BE,
∴∠ABE=90°,∠BAE=45°,
∴AB=BE,∠ABO+∠EBF=90°,
又∵∠ABO+∠OAB=90°,
∴∠OAB=∠EBF,
在△AOB和△BFE中,
,
∴△AOB≌△BFE(AAS),
∴BF=OA=2,EF=OB=1,
∴OF=3,
∴点E的坐标为(3,1),
设直线AC的解析式为y=kx+b,
由题意可得
,
解得
,
∴直线AC的解析式为y=﹣x+2,
令y=0,解得x=6,
∴D(6,0).
26.解:(1)如图1,连接AC,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,
∴∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAC=∠PAE,
∴∠BAP=∠CAE,
在△BAP和△CAE中,
,
∴△BAP≌△CAE(SAS),
∴BP=CE,∠ABP=∠ACE=30°,
延长CE交AD于H,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD,
故答案为:BP=CE,CE⊥AD;
(2)当点P在线段BD延长线上时,(1)中的结论还成立,
理由如下:
如图2,连接AC交BD于O,设CE交AD于H,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAP=∠CAE,
在△BAP和△CAE中,
,
∴△BAP≌△CAE(SAS),
∴BP=CE,∠ABP=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD;
(3)如图3,连接AC交BD于O,连接CE,作EH⊥AP于H,
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC,
∴∠ABO=30°,
∴AO=1,BO=DO=,
∴BD=2,
由(2)知CE⊥AD,
∵AD∥BC,
∴CE⊥BC,
∵BE=,BC=AB=2,
∴CE===3,
∴由(2)知BP=CE=3,
∴DP=BP﹣BD=3﹣2=,
∴OP=2,
∴AP===,
∵△APE是等边三角形,
∴AH=AP=,AE=AP=EP=,
∴EH==,
∵S四边形ADPE=S△ADP+S△APE,
∴S四边形ADPE=DP?AO+AP?EH=××1+××=,
∴四边形ADPE的面积是.
一.选择题(共10小题,满分40分,每小题4分)
1.下列条件中,使△ABC不是直角三角形的是( )
A.a=3,b=4,c=5
B.a2+b2=c2
C.a:b:c=2:2:3
D.∠A:∠B:∠C=1:2:3
2.下列图案中是中心对称图形但不是轴对称图形的是( )
A.
B.
C.
D.
3.“新冠病毒”的英语“Novelcoronavirus”中,字母“n”出现的频率是( )
A.
B.
C.2
D.1
4.如图,在平行四边形ABCD中,若点E是BD的中点,点M是AD上一动点,连接MB,MC,ME,并延长ME交BC于点N,设MD=tAM,有以下结论:①当t=1时,则BM=CM;②当t=2时,则S△MNC=S△EBM;③若△ABM≌△NMC,则MN⊥BD.其中正确的是( )
A.①
B.②
C.③
D.②③
5.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD
B.∠ABD=∠CBD
C.AB=BC
D.AC=BD
6.在同一直角坐标系中,一次函数y=kx+b和y=bx+k的图象可能正确的是( )
A.
B.
C.
D.
7.点P1(x1,y1),点P2(x2,y2)是一次函数y=﹣4x+3图象上的两个点,且x1>x2,则y1与y2的大小关系是( )
A.y1<y2
B.y1>y2
C.y1>y2>0
D.y1=y2
8.如图,∠MON=60°,OA平分∠MON,P是射线OA上的一点,且OP=4,若点Q是射线OM上的一个动点,则PQ的最小值为( )
A.1
B.2
C.3
D.4
9.如图,在矩形ABCD中,AB=m,BC=6,点E在边CD上,且CE=m.连接BE,将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,则m=( )
A.3
B.2
C.
D.5
10.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t=或t=,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,满分32分,每小题4分)
11.函数y=中,自变量x的取值范围是
.
12.已知一个n边形的内角和等于1980°,则n=
.
13.有人做过掷硬币的实验,掷一枚一元硬币4040次,结果正面(有国徽的一面)向上的次数为2048次,则正面向上的频率是
(保留两位有效数字).
14.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是
.
15.已知一次函数y=2x+5,当﹣2≤x≤6时,y的最大值是
.
16.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、AD的中点,EF=3,则AB的长度为
.
17.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有
个.
18.如图,正方形ABCD中,点E、F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为
.
三.解答题(共8小题,满分78分)
19.(8分)如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.
(1)求证△AMB≌△CNA;
(2)求证∠BAC=90°.
20.(8分)为了解某校七年级学生的跳高水平,随机抽取该年级60名学生进行跳高测试,并把测试成绩分成四组,绘制成如图所示的频数表和未完成的频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校七年级60名学生跳高测试成绩的频数表
组别(m)
频数
1.09~1.19
8
1.19~1.29
16
1.29~1.39
a
1.39~1.49
12
(1)求a的值;
(2)把频数分布直方图补充完整;
(3)求跳高成绩在1.29m(含1.29m)以上的学生数占参加测试学生数的百分比.
21.(8分)如图,在平面直角坐标系中,A(﹣5,3)、B(﹣4,4)、C(﹣3,2).
(1)将△ABC向下平移4个单位,再向右平移2个单位,画出平移后的图形△A1B1C1
(2)画出△ABC关于直线x=﹣1的对称图形△A2B2C2
(3)求△ABC的面积
S△ABC.
22.(10分)如图,在△ABC中,AB=AC,点E、F分别是BC、AC边上的中点,过点A作AD∥BC,交EF的延长线于点D
(1)求证:四边形ABED是平行四边形;
(2)若AB=4,∠BAC=120°,求四边形ABED的周长.
23.(10分)元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
24.(10分)如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AE=8,AB=4,求PE的长.
25.(12分)(1)如图1,在四边形ABCD中,∠B=∠C=90°,点E是边BC上一点,AB=EC,BE=CD,连接AE、DE,求证△AED是等腰直角三角形.
(2)如图2,一次函数y=﹣2x+2的图象与y轴交于点A,与x轴交于点B,直线AC交x轴于点D,且∠CAB=45°,则点D的坐标为
.
26.(12分)在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE.
(1)如图1,当点P在线段BD上时,连接CE,BP与CE的数量关系是
;CE与AD的位置关系是
;
(2)当点P在线段BD的延长线上时,(1)中的结论是否还成立?若成立,请予以证明,若不成立,请说明理由;(请结合图2的情况予以证明或说理)
(3)如图3,在(2)的条件下,连接BE,若AB=2,BE=,求四边形ADPE的面积.
参考答案
一.选择题(共10小题,满分40分,每小题4分)
1.解:A、∵32+42=52,∴△ABC是直角三角形,不符合题意;
B、∵a2+b2=c2,∴△ABC是直角三角形,不符合题意;
C、∵22+22≠32,∴△ABC不是直角三角形,符合题意;
D、∵∠A:∠B:∠C=1:2:3,∴∠C=90°,∴△ABC是直角三角形,不符合题意;
故选:C.
2.解:A、是中心对称图形,也是轴对称图形,不符合题意;
B、不是中心对称图形,是轴对称图形,不符合题意;
C、是中心对称图形,不是轴对称图形,符合题意;
D、不是轴对称图形,也不是中心对称图形,不符合题意.
故选:C.
3.解:在“Novelcoronavirus”中,字母的总数是16,字母“n”有2个,
因而字母“n”出现的频率是:=.
故选:B.
4.解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠BDA=∠DBC,
∵点E是BD的中点,
∴DE=BE,
在△DME和△BNE中,
,
∴△DME≌△BNE(ASA),
∴DM=BN,ME=NE,
∵t=1,
∴AM=DM=AD,
∴BN=BC=CN,
∴只有当MN⊥BC时,CM=BM,
∴①错误,
当t=2时,则DM=2AM,
∴BN=2CN,
∴S△BMN=2S△MNC,
∵ME=EN,
∴S△BEM=S△BMN,
∴S△BEM=S△MNC,
故②正确,
若△ABM≌△NMC,则BM=MC,当BM不一定等于BN,
∴MN⊥BD不一定成立,故③错误,
故选:B.
5.解:添加AC=BD,理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,
故选:D.
6.解:A、一条直线反映k>0,b>0,一条直线反映k>0,b<0,故本选项错误;
B、一条直线反映出k>0,b<0,一条直线反映k>0,b<0,一致,故本选项正确;
C、一条直线反映k<0,b>0,一条直线反映k>0,b<0,故本选项错误;
D、一条直线反映k>0,b<0,一条直线反映k<0,b<0,故本选项错误.
故选:B.
7.解:∵k=﹣4<0,
∴y随x的增大而减小,
又∵x1>x2,
∴y1<y2.
故选:A.
8.解:作PQ′⊥OM于Q′,
∵∠MON=60°,OP平分∠MON,
∴∠POQ′=30°,
∴PQ′=OP=2,
由垂线段最短可知,PQ的最小值是2,
故选:B.
9.解:∵四边形ABCD是矩形,
∴AD=BC=6,CD=AB=m,∠A=∠D=∠C=90°.
∵将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,
∴BC'=BC=6,∠BC'E=∠C=90°,C'E=CE=m,DE=CD﹣CE=m﹣m=m,
∴DE=C'E,
∴∠DC'E=30°,
∴∠AC'B=180°﹣90°﹣30°=60°,
∴AB=BC'×sin∠AC'B=6×=3,
即m=3;
故选:A.
10.解:由图象可知A、B两城市之间的距离为300km,故①正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
把y=150代入y甲=60t,可得:t=2.5,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(2.5,150)代入可得,
解得,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
乙的速度:150÷(2.5﹣1)=100,
乙的时间:300÷100=3,
甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故②正确;
甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③错误;
令|y甲﹣y乙|=40,可得|60t﹣100t+100|=40,即|100﹣40t|=40,
当100﹣40t=40时,可解得t=,
当100﹣40t=﹣40时,可解得t=,
又当t=时,y甲=40,此时乙还没出发,
当t=时,乙到达B城,y甲=260;
综上可知当t的值为或或或t=时,两车相距40千米,故④不正确;
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
11.解:根据题意,得:,
解得:x≤2且x≠﹣2,
故答案为:x≤2且x≠﹣2.
12.解:设这个多边形的边数为n,
则(n﹣2)?180°=1980°,
解得n=13.
故答案为:13.
13.解:掷一枚一元硬币4040次,结果正面(有国徽的一面)向上的次数为2048次,
则正面向上的频率是2048÷4040≈0.51.
14.解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,
∴1+m=3、1﹣n=2,
解得:m=2、n=﹣1,
所以m+n=2﹣1=1,
故答案为:1.
15.解:∵一次函数y=2x+5,
∴该函数的图象y随x的增大而增大,
∵﹣2≤x≤6,
∴当x=6时,y取得最大值,此时y=17,
故答案为:17.
16.解:∵E、F分别是AC、AD的中点,
∴AE=EC,AF=DF,
∴EF∥CD,CD=2EF,
∵EF=3,
∴CD=6,
∵∠ACB=90°,D是AB的中点,
∴AB=2CD=12,
故答案为12.
17.解:A1B1C1D1四条边上的整点共有8个,即4+4×1=8,
A2B2C2D2四条边上的整点共有16个,即4+4×3=16,
正方形A3B3C3D3四条边上的整点的个数有4+4×5=24,
…正方形A10B10C10D10四条边上的整点的个数有:4+4×19=80,
故答案为:80.
18.解:∵四边形ABCD为正方形,BC=4,
∴∠CDF=∠BCE=90°,AD=DC=BC=4,
又∵DE=AF=1,
∴CE=DF=3,
∴在△CDF和△BCE中,
,
∴△CDF≌△BCE(SAS),
∴∠DCF=∠CBE,
∵∠DCF+∠BCF=90°,
∴∠CBE+∠BCF=90°,
∴∠BGC=90°,
∵在Rt△BCE中,BC=4,CE=3,
∴BE=5,
∴BE?CG=BC?CE,
∴CG===,
∵△CDF≌△BCE(SAS),
∴CF=BE=5,
∴GF=CF﹣CG=5﹣=2.6.
故答案为:2.6.
三.解答题(共8小题,满分66分)
19.证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL);
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
20.解:(1)a=60﹣8﹣16﹣12=24(人),
答:a的值为24;
(2)补全频数分布直方图如下:
(3)×100%=60%,
答:跳高成绩在1.29m(含1.29m)以上的学生数占参加测试学生数的60%.
21.解:如图,添加网格结构,
(1)如图所示,△A1B1C1为所求作的三角形;
(2)△A2B2C2为所求作的三角形;
(3)S△ABC=2×2﹣×1×1﹣×1×2﹣×1×2=4﹣﹣1﹣1=1.5.
22.(1)证明:∵点E、F分别是BC、AC边上的中点
∴DE∥AB,
又AD∥BC,
∴四边形ABED是平行四边形;
(2)解:连接AE,
∵AB=AC,点E是BC边上的中点,
∴∠AEB=90°,∠BAE==60°,
∴∠ABE=30°,
∴在Rt△ABE中,,∴,
由(1)知,四边形ABED是平行四边形,
∴四边形ABED的周长=.
23.解:(1)设OA段图象的函数表达式为y=kx.
∵当x=0.8时,y=48,
∴0.8k=48,
∴k=60.
∴y=60x(0≤x≤0.8),
∴当x=0.5时,y=60×0.5=30.
故小黄出发0.5小时时,离家30千米;
(2)设AB段图象的函数表达式为y=k′x+b.
∵A(0.8,48),B(2,156)在AB上,
,
解得,
∴y=90x﹣24(0.8≤x≤2);
(3)∵当x=1.5时,y=90×1.5﹣24=111,
∴156﹣111=45.
故小黄出发1.5小时时,离目的地还有45千米.
24.(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵PB=PE,
∴四边形BPEQ是菱形;
(2)解:设PE=BP=x,则AP=8﹣x,
在Rt△ABP中,AP2+AB2=BP2,
即(8﹣x)2+42=x2,
解得x=5,
∴PE=5.
25.(1)证明:∵在△ABE和△ECD中,
,
∴△ABE≌△ECD
(SAS),
∴AE=DE,∠AEB=∠EDC,
在Rt△EDC中,∠C=90°,
∴∠EDC+∠DEC=90°.
∴∠AEB+∠DEC=90°.
∵∠AEB+∠DEC+∠AED=180°,
∴∠AED=90°.
∴△AED是等腰直角三角形;
(2)解:如图2,过点B作BE⊥AB,交AD于点E,过点E作EF⊥OD,交OD于点F,
把x=0代入y=﹣2x+2中,得y=2,
∴点A的坐标为(0,2),
∴OA=2,
把y=0代入y=﹣2x+2,得﹣2x+2=0,解得x=1,
∴点B的坐标为(1,0),
∴OB=1,
∵AO⊥OB,EF⊥BD,
∴∠AOB=∠BFE=90°,
∵AB⊥BE,
∴∠ABE=90°,∠BAE=45°,
∴AB=BE,∠ABO+∠EBF=90°,
又∵∠ABO+∠OAB=90°,
∴∠OAB=∠EBF,
在△AOB和△BFE中,
,
∴△AOB≌△BFE(AAS),
∴BF=OA=2,EF=OB=1,
∴OF=3,
∴点E的坐标为(3,1),
设直线AC的解析式为y=kx+b,
由题意可得
,
解得
,
∴直线AC的解析式为y=﹣x+2,
令y=0,解得x=6,
∴D(6,0).
26.解:(1)如图1,连接AC,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,
∴∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAC=∠PAE,
∴∠BAP=∠CAE,
在△BAP和△CAE中,
,
∴△BAP≌△CAE(SAS),
∴BP=CE,∠ABP=∠ACE=30°,
延长CE交AD于H,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD,
故答案为:BP=CE,CE⊥AD;
(2)当点P在线段BD延长线上时,(1)中的结论还成立,
理由如下:
如图2,连接AC交BD于O,设CE交AD于H,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAP=∠CAE,
在△BAP和△CAE中,
,
∴△BAP≌△CAE(SAS),
∴BP=CE,∠ABP=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD;
(3)如图3,连接AC交BD于O,连接CE,作EH⊥AP于H,
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC,
∴∠ABO=30°,
∴AO=1,BO=DO=,
∴BD=2,
由(2)知CE⊥AD,
∵AD∥BC,
∴CE⊥BC,
∵BE=,BC=AB=2,
∴CE===3,
∴由(2)知BP=CE=3,
∴DP=BP﹣BD=3﹣2=,
∴OP=2,
∴AP===,
∵△APE是等边三角形,
∴AH=AP=,AE=AP=EP=,
∴EH==,
∵S四边形ADPE=S△ADP+S△APE,
∴S四边形ADPE=DP?AO+AP?EH=××1+××=,
∴四边形ADPE的面积是.
同课章节目录
