平行四边形的判定
图片预览



文档简介
(共21张PPT)
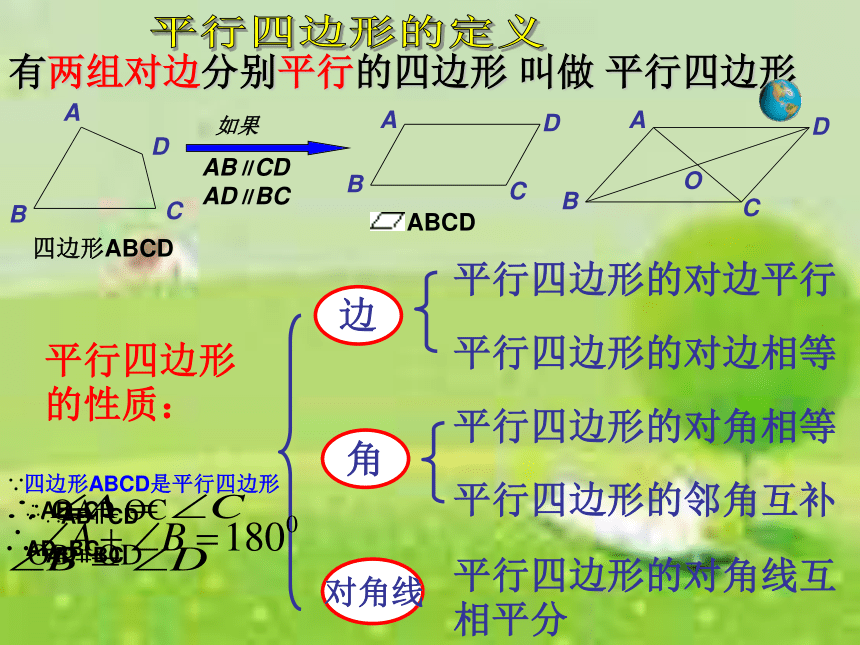
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
平行 四边形的两组对边分别相等;
平行 四边形的两组对角分别相等;
我们得到的这些逆命题都成立吗?我们一起探讨一下吧:
平行 四边形的对角线互相 平 分。
思考:我们已经学 行 四边形的这些性质,那么它们的逆命题各是什么呢?
两组对角分别相等的四边形是平 行 四边形;
对角线互相平 分的四边形是平 行 四边形。
两组对边分别相等的四边形是平 行 四边形;
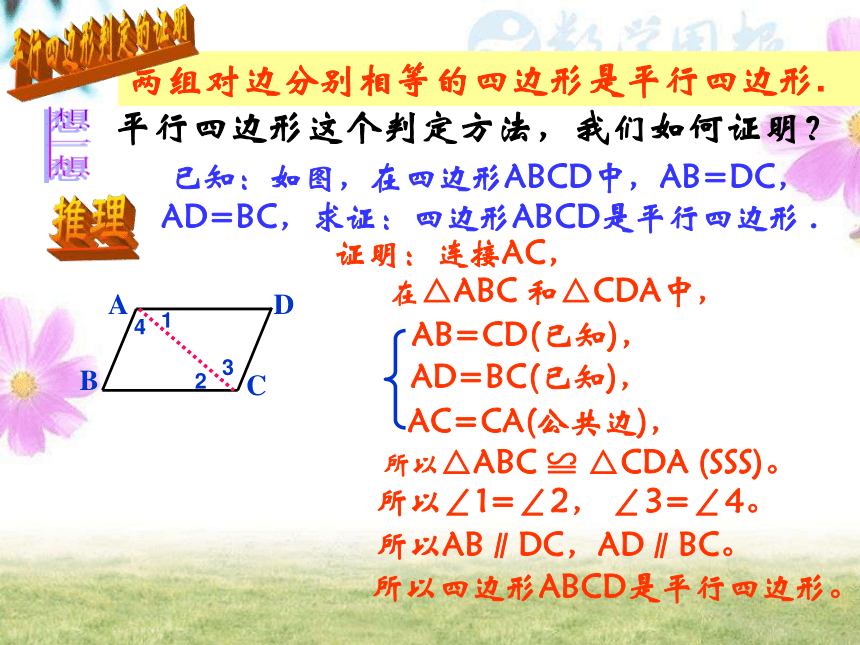
两组对边分别相等的四边形是平行四边形.
平行四边形这个判定方法,我们如何证明?
A
B
C
D
证明:连接AC,
所以AB∥DC,AD∥BC。
4
1
2
3
所以∠1=∠2, ∠3=∠4。
AC=CA(公共边),
所以△ABC ≌ △CDA (SSS)。
AD=BC(已知),
已知:如图,在四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形 .
AB=CD(已知),
在△ABC 和△CDA中,
所以四边形ABCD是平行四边形。
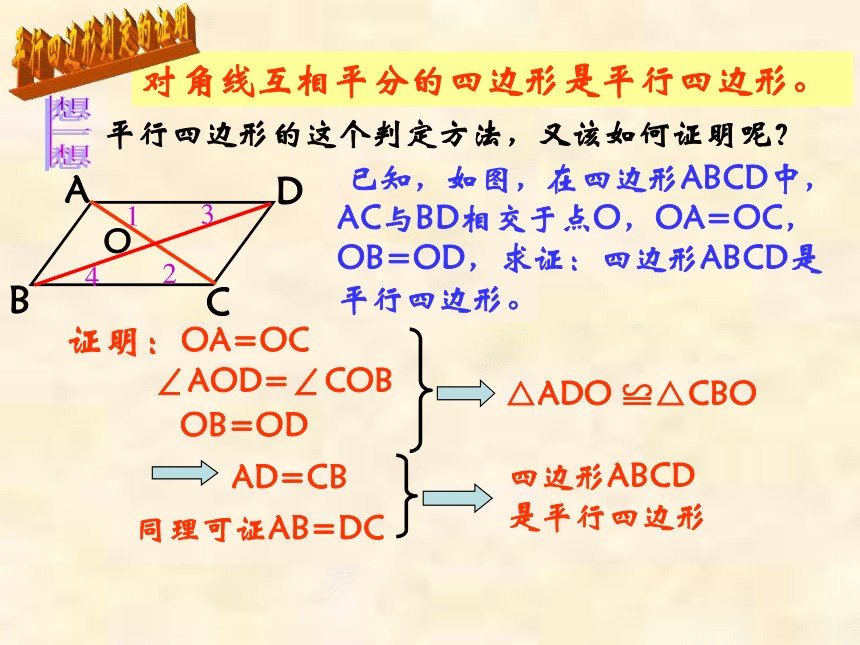
对角线互相平分的四边形是平行四边形。
已知,如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD,求证:四边形ABCD是平行四边形。
A
B
C
D
1
2
3
4
O
同理可证AB=DC
△ADO ≌△CBO
AD=CB
OA=OC
证明:
平行四边形的这个判定方法,又该如何证明呢?
OB=OD
∠AOD=∠COB
四边形ABCD是平行四边形
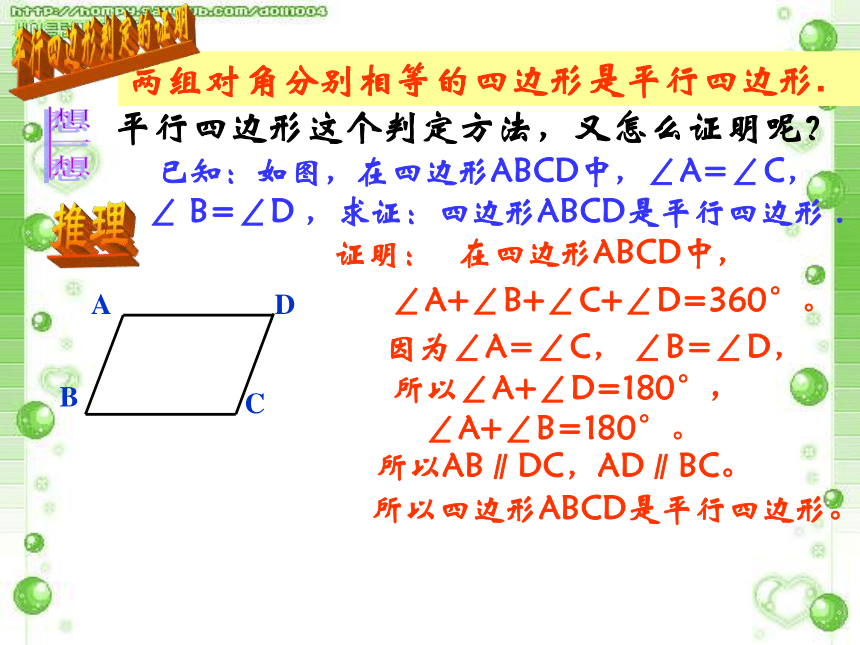
两组对角分别相等的四边形是平行四边形.
平行四边形这个判定方法,又怎么证明呢?
A
B
C
D
证明:
所以AB∥DC,AD∥BC。
∠A+∠B+∠C+∠D=360°。
已知:如图,在四边形ABCD中,∠A=∠C, ∠ B=∠D ,求证:四边形ABCD是平行四边形 .
在四边形ABCD中,
所以四边形ABCD是平行四边形。
因为∠A=∠C, ∠B=∠D,
所以∠A+∠D=180°,
∠A+∠B=180°。
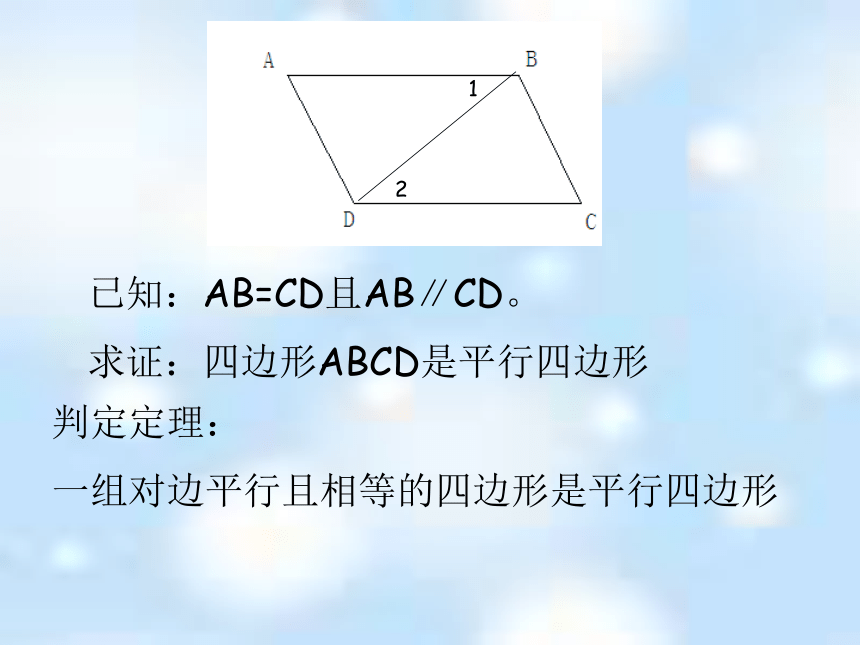
2
1
已知:AB=CD且AB∥CD。
求证:四边形ABCD是平行四边形
判定定理:
一组对边平行且相等的四边形是平行四边形
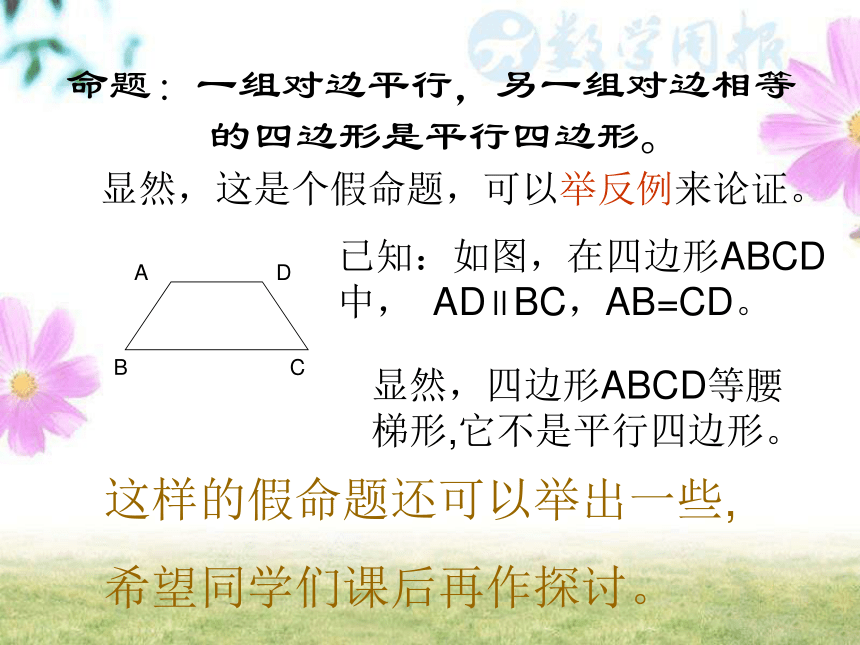
命题:一组对边平行,另一组对边相等
的四边形是平行四边形。
显然,这是个假命题,可以举反例来论证。
A
B
C
D
已知:如图,在四边形ABCD中, AD∥BC,AB=CD。
显然,四边形ABCD等腰梯形,它不是平行四边形。
这样的假命题还可以举出一些,
希望同学们课后再作探讨。
从边来判定
1、两组对边分别平行的四边形是平行四边形(定义)
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
四、理一理
平行四边形的判定方法
1、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
巩固练习
2、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
(两组对角分别相等)
A
B
D
C
3、如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?
F
A
B
C
D
E
解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF
AD∥BC
AB=DC
AD=BC
四边形ABCD是平行四边形
AB∥DC
DC∥EF
DC=EF
DE=CF
四边形CDEF是平行四边形
DE∥CF
AB∥ DC∥EF
理由如下:
大显身手
D
A
B
C
E
F
证明:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
3、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
大显身手
3、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形
D
A
B
C
E
F
改一改,证一证
BE∥DF
5、如图,在 ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。
A
D
C
B
E
F
G
H
O
5.已知:如图,E,F分别是平行四边形ABCD 的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED BF.
∥
﹦
∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
6.已知:如图,AD⊥AC,BC⊥AC,且AB=CD.
求证:AB∥CD.
D
C
A
B
证明:
∵AD⊥AC, BC⊥AC,
∴AD∥BC, ∠BCA=∠DAC=90O,
又∵AB=CD, AC=CA,
∴Rt⊿ACB≌Rt⊿CAD.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)。
∴AB∥CD(平行四边形的定义)。
练习:
6、如图,在□ABCD中,延长AD到F,使
DF=AD,连结BF交CD于点E .
求证:点E平分CD与BF.
如图,l1 // l2 , 线段AB//CD//EF, 且点A、C、E在l1上,B、D、F在l2上,则AB、CD、EF的长短相等吗?为什么?
l
1
l
2
E
F
C
D
A
B
夹在两平行线间的平行线段相等。
l
1
l
2
E
F
C
D
A
B
∟
∟
∟
如图,l1 // l2 ,点A、C、E在l1上,线段AB、CD、EF都垂直与l2 ,垂足分别为B、D、F,则AB、CD、EF的长短相等吗?为什么?
一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离。
平行线间的距离处处相等
它与点与点的距离、点到直线的距离的联系与区别
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
平行 四边形的两组对边分别相等;
平行 四边形的两组对角分别相等;
我们得到的这些逆命题都成立吗?我们一起探讨一下吧:
平行 四边形的对角线互相 平 分。
思考:我们已经学 行 四边形的这些性质,那么它们的逆命题各是什么呢?
两组对角分别相等的四边形是平 行 四边形;
对角线互相平 分的四边形是平 行 四边形。
两组对边分别相等的四边形是平 行 四边形;
两组对边分别相等的四边形是平行四边形.
平行四边形这个判定方法,我们如何证明?
A
B
C
D
证明:连接AC,
所以AB∥DC,AD∥BC。
4
1
2
3
所以∠1=∠2, ∠3=∠4。
AC=CA(公共边),
所以△ABC ≌ △CDA (SSS)。
AD=BC(已知),
已知:如图,在四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形 .
AB=CD(已知),
在△ABC 和△CDA中,
所以四边形ABCD是平行四边形。
对角线互相平分的四边形是平行四边形。
已知,如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD,求证:四边形ABCD是平行四边形。
A
B
C
D
1
2
3
4
O
同理可证AB=DC
△ADO ≌△CBO
AD=CB
OA=OC
证明:
平行四边形的这个判定方法,又该如何证明呢?
OB=OD
∠AOD=∠COB
四边形ABCD是平行四边形
两组对角分别相等的四边形是平行四边形.
平行四边形这个判定方法,又怎么证明呢?
A
B
C
D
证明:
所以AB∥DC,AD∥BC。
∠A+∠B+∠C+∠D=360°。
已知:如图,在四边形ABCD中,∠A=∠C, ∠ B=∠D ,求证:四边形ABCD是平行四边形 .
在四边形ABCD中,
所以四边形ABCD是平行四边形。
因为∠A=∠C, ∠B=∠D,
所以∠A+∠D=180°,
∠A+∠B=180°。
2
1
已知:AB=CD且AB∥CD。
求证:四边形ABCD是平行四边形
判定定理:
一组对边平行且相等的四边形是平行四边形
命题:一组对边平行,另一组对边相等
的四边形是平行四边形。
显然,这是个假命题,可以举反例来论证。
A
B
C
D
已知:如图,在四边形ABCD中, AD∥BC,AB=CD。
显然,四边形ABCD等腰梯形,它不是平行四边形。
这样的假命题还可以举出一些,
希望同学们课后再作探讨。
从边来判定
1、两组对边分别平行的四边形是平行四边形(定义)
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
四、理一理
平行四边形的判定方法
1、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
巩固练习
2、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
(两组对角分别相等)
A
B
D
C
3、如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?
F
A
B
C
D
E
解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF
AD∥BC
AB=DC
AD=BC
四边形ABCD是平行四边形
AB∥DC
DC∥EF
DC=EF
DE=CF
四边形CDEF是平行四边形
DE∥CF
AB∥ DC∥EF
理由如下:
大显身手
D
A
B
C
E
F
证明:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
3、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
大显身手
3、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形
D
A
B
C
E
F
改一改,证一证
BE∥DF
5、如图,在 ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。
A
D
C
B
E
F
G
H
O
5.已知:如图,E,F分别是平行四边形ABCD 的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED BF.
∥
﹦
∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
6.已知:如图,AD⊥AC,BC⊥AC,且AB=CD.
求证:AB∥CD.
D
C
A
B
证明:
∵AD⊥AC, BC⊥AC,
∴AD∥BC, ∠BCA=∠DAC=90O,
又∵AB=CD, AC=CA,
∴Rt⊿ACB≌Rt⊿CAD.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)。
∴AB∥CD(平行四边形的定义)。
练习:
6、如图,在□ABCD中,延长AD到F,使
DF=AD,连结BF交CD于点E .
求证:点E平分CD与BF.
如图,l1 // l2 , 线段AB//CD//EF, 且点A、C、E在l1上,B、D、F在l2上,则AB、CD、EF的长短相等吗?为什么?
l
1
l
2
E
F
C
D
A
B
夹在两平行线间的平行线段相等。
l
1
l
2
E
F
C
D
A
B
∟
∟
∟
如图,l1 // l2 ,点A、C、E在l1上,线段AB、CD、EF都垂直与l2 ,垂足分别为B、D、F,则AB、CD、EF的长短相等吗?为什么?
一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离。
平行线间的距离处处相等
它与点与点的距离、点到直线的距离的联系与区别
