黑龙江省鸡西密山市(五四学制)2020-2021学年九年级上学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 黑龙江省鸡西密山市(五四学制)2020-2021学年九年级上学期期末考试数学试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 281.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览




文档简介
2020—2021学年度第一学期期末质量监测
九年级数学试卷(120分钟)
题号
一
二
三
总
分
21
22
23
24
25
26
27
28
得分
一选择题(每小题3分,满分30分
1.下列图形绕某点旋转90°后,不能与原来图形重合的是( )
A.
B.
C.
D.
2.已知二次函数,在其图象对称轴的左侧,y随x的增大而减小,则a的值为( )
A.
B.±
C.﹣
D.0
3.下列说法正确的是(
)
A.
“明天降雨的概率是80%”表示明天有80%的时间降雨
B.
“抛一枚硬币正面朝上的概率是0.5”
表示每抛一枚硬币2次就有一次正面朝上出现
C.
“彩票中奖的概率是1%”
表示买100张彩票一定会中奖
D.
“抛一枚正方体骰子朝上面的数为奇数的概率是0.5”表示如果这个骰子抛很多很多次,那么平均每2次就有1次出现朝上面的数为奇数。
4.已知点,
.
三点都在反比例函数的图像上,则下列关系正确的是(
).
A.
B.
C.
D.
5.反比例,在第一象限的图象如右图所示,其中的解
析式为,过图象上的任意一点,作轴的平行线交图象于,交轴于,若,则的解析式是
B.
C.
D.
6.如右图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则sinE的值为( )
A.
B.
C.
D.
7.如右图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则NM:MC等于( )
A.1:2
B.1:3
C.1:4
D.1:5
8.如右图,菱形ABCD的对角线AC,BD相较于O,过点D作DH⊥AB于H,连接OH,若OA=6,菱形ABCD的面积,则OH的长为(
)
A.6
B.8
C.
D.4
在数学知识竞赛,为奖励成绩突出的学生,九年一班计划用200元购买A,B.C三种奖品,A种每个十元,B种每个20元,C种每个30元,在C种奖品不超过两个且钱全部用完的情况下,有多少种购买方案?
A.12
B.14
C.16
D.15
10.已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )
A.y1<y3<y2
B.y2<y3<y1
C.y3<y2<y1
D.y3<y1<y2
二.填空题(每小题3分,满分30分)
11.已知点A(a,b)绕着(0,﹣1)旋转180°得到B(﹣4,1),则A点坐标为
.
12.
已知二次函数y=2x2+2021,当x分别取x1,x2(x1≠x2)时,函数值相等,则当x取2x1+2x2时,函数值为
13.在一个不透明的盒子里有2个红球和n个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到红球的概率是,则n的值为
.
14如右图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC=
.
(第14题图)
15.如右图所示,在△ABC中,∠ACB=90°,CD是AB边上的中线,AC=6,CD=5,则sin
A等于________.
16.已知锐角A的正弦sin
A是一元二次方程2x2-7x+3=0的根,则sin
A=________.
17.数y=ax2﹣2ax+m(a>0)的图象过点(2,0),那么使函数值y<0成立的x的取值范围是
.
18.如右图,AB是⊙O的直径,点C、D在⊙O上,若∠ACD=25°,则∠BOD的度数为
.
19.如下图,PA、PB切⊙O于A、B,点C在上,DE切⊙O于C交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是
.
(第19图题)
(第20图题)
20.如上图,△ABC中,D在BC上,F是AD的中点,连CF并延长交AB于E,已知=,则等于
.
三.解答题(满分60分)
21.(5分)先化简,再求值:,其中
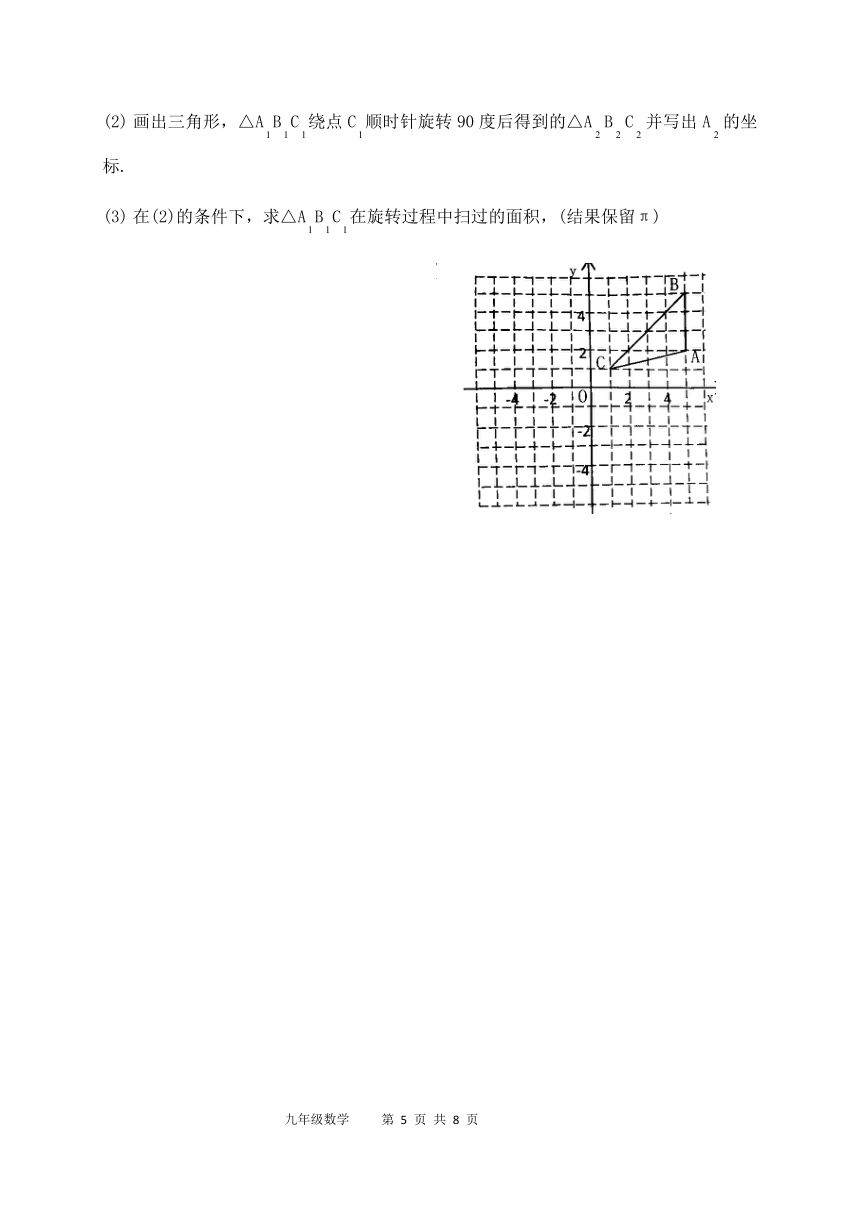
22.(7分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点,A(5,2),B(5,5),C(1,1)均在格点上,
将△ABC向左平移五个单位,单位得到△ABC,并求出点A坐标,
画出三角形,△ABC绕点C顺时针旋转90度后得到的△ABC并写出A的坐标.
在(2)的条件下,求△ABC在旋转过程中扫过的面积,(结果保留π)
23.(7分)已知二次函数的图象如图所示,它与轴的一个交点坐标为,与轴的交点坐标为.
(1)求此二次函数的表达式,并用配方法求顶点的坐标;
(2)直接写出当函数值时,自变量的取值范围.
24.(8分)
如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.
25(7分)如图,一次函数的图象与反比例函数的图象交于,两点,
求一次函数和反比例函数的表达式;
求的面积.
26(8分)一如图,海上有一灯塔P,在它周围3海里处有暗礁,一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在北偏东60°方向上,继续行驶20分钟后,到达B处又测得灯塔P在北偏东45°方向上,问客轮不改变方向继续前进有无触礁危险?
27.(8分)如图,已知在⊙O中,AB是⊙O的直径,AC=8,BC=6.
(1)求⊙O的面积;
(2)若D为⊙O上一点,且△ABD为等腰三角形,求CD的长.
28(10分)二如图,抛物线经过、、三点.
求抛物线的解析式;
如图①,在抛物线的对称轴上是否存在点,使得四边形的周长最小?若存在,求出四边形周长的最小值;若不存在,请说明理由.
如图②,点是线段上一动点,连接,在线段上是否存在这样的点,使为等腰三角形且为直角三角形?若存在,求点的坐标;若不存在,请说明理由.
密山市2020—2021学年第一学期期末质量检测
九年级数学答案
一.ACDBC
AADBD20.解:作DG∥CE,如图∵DG∥CE,∴==,设BG=2x,则GE=3x,∵EF∥DG,∴==1,∴AE=EG=3x,∴==.故答案为:.
二.11.(4.-3)
12.2021
13.8
14.5
15
16.
17.018.130?19.24
20.(20.解:作DG∥CE,如图∵DG∥CE,∴==,设BG=2x,则GE=3x,∵EF∥DG,∴==1,∴AE=EG=3x,∴==.故答案为:)
21.原式= --3分 代入,原式=--2分
22
(1)A(0.2)--2分(2)A(-3.-3)--2分
-----3分
23解:(1)由二次函数的图象经过和两点,
得,
解这个方程组,得
,
抛物线的解析式为,
由于,
则抛物线的顶点坐标为.--4分(2)令,得.
解这个方程,得,.
∴此二次函数的图象与轴的另一个交点的坐标为.
当时,.----3分
24.(1)证明:∵四边形EFMN是正方形,
∴EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴△AEF∽△ABC.---3分
(2)解:设正方形EFMN的边长为x.
∵△AEF∽△ABC,AD⊥BC,
∴=,
∴=,
∴x=8,
∴正方形的边长为8cm---5分
25解:∵点在的图象上,
∴,
∴反比例函数为,
又∵在的图象上,
∴,解得,
∴,
∵和都在直线上,
∴,解得,
∴一次函数解析式为;----4分
设直线与轴交于点,如图,
当时,,解得,则,
∴.---3分
26.解:过P作PC⊥AB于C点,如图,
(第24题)
据题意知AB=9×=3,--1分
∠PAB=90°-60°=30°,[]
∠PBC=90°-45°=45°,∠PCB=90°,∴PC=BC.--2分
在Rt△APC中,tan
30°===,--2分
即=,∴PC=海里>3海里,
∴客轮不改变方向继续前进无触礁危 --- 3分
27.解:(1)∵AB是⊙O的直径,
∴∠ACB=90°.
∴AC=8,BC=6,
∴AB=10.
∴⊙O的面积=π×52=25π;--2分
(2)作直径DD′⊥AB,BH⊥CD于H,如图,则=,
∴AD=BD,∠ACD=∠BCD=45°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴△ADB为等腰直角三角形,
∴DB=AB=5,
易得△BCH为等腰直角三角形,
∴CH=BH=BC=3,
在Rt△BDH中,DH==4,
∴CD=CH+DH=3+4=7,----4分
∵DD′是⊙O的直径,
∴∠DCD′=90°,
∴CD′==,
综上所述,CD的长为或7.
------2分
28.解:由已知得解得.
所以,抛物线的解析式为.---3分
∵、关于对称轴对称,如图,连接,
∴与对称轴的交点即为所求的点,此时,
∴四边形的周长最小值为:,
∵、、,
∴,,,
∴;
∴在抛物线的对称轴上存在点,使得四边形的周长最小,四边形周长的最小值为.----3分
∵、,
∴直线的解析式为,
①当时,如图,设,
∵,
∴只能,
∵轴,
∴,
∴,即,解得,
代入得,,解得,
∴;
②当时,如图,
∵,
∴只能,
设,
∴,
∵,,
∴,
∴,解得,
作,
∴,即,
∴,,
∴,
∴,
综上,在线段上存在这样的点,使为等腰三角形且为直角三角形,点的坐标为或.
----4分
九年级数学
九年级数学试卷(120分钟)
题号
一
二
三
总
分
21
22
23
24
25
26
27
28
得分
一选择题(每小题3分,满分30分
1.下列图形绕某点旋转90°后,不能与原来图形重合的是( )
A.
B.
C.
D.
2.已知二次函数,在其图象对称轴的左侧,y随x的增大而减小,则a的值为( )
A.
B.±
C.﹣
D.0
3.下列说法正确的是(
)
A.
“明天降雨的概率是80%”表示明天有80%的时间降雨
B.
“抛一枚硬币正面朝上的概率是0.5”
表示每抛一枚硬币2次就有一次正面朝上出现
C.
“彩票中奖的概率是1%”
表示买100张彩票一定会中奖
D.
“抛一枚正方体骰子朝上面的数为奇数的概率是0.5”表示如果这个骰子抛很多很多次,那么平均每2次就有1次出现朝上面的数为奇数。
4.已知点,
.
三点都在反比例函数的图像上,则下列关系正确的是(
).
A.
B.
C.
D.
5.反比例,在第一象限的图象如右图所示,其中的解
析式为,过图象上的任意一点,作轴的平行线交图象于,交轴于,若,则的解析式是
B.
C.
D.
6.如右图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则sinE的值为( )
A.
B.
C.
D.
7.如右图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则NM:MC等于( )
A.1:2
B.1:3
C.1:4
D.1:5
8.如右图,菱形ABCD的对角线AC,BD相较于O,过点D作DH⊥AB于H,连接OH,若OA=6,菱形ABCD的面积,则OH的长为(
)
A.6
B.8
C.
D.4
在数学知识竞赛,为奖励成绩突出的学生,九年一班计划用200元购买A,B.C三种奖品,A种每个十元,B种每个20元,C种每个30元,在C种奖品不超过两个且钱全部用完的情况下,有多少种购买方案?
A.12
B.14
C.16
D.15
10.已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )
A.y1<y3<y2
B.y2<y3<y1
C.y3<y2<y1
D.y3<y1<y2
二.填空题(每小题3分,满分30分)
11.已知点A(a,b)绕着(0,﹣1)旋转180°得到B(﹣4,1),则A点坐标为
.
12.
已知二次函数y=2x2+2021,当x分别取x1,x2(x1≠x2)时,函数值相等,则当x取2x1+2x2时,函数值为
13.在一个不透明的盒子里有2个红球和n个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到红球的概率是,则n的值为
.
14如右图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC=
.
(第14题图)
15.如右图所示,在△ABC中,∠ACB=90°,CD是AB边上的中线,AC=6,CD=5,则sin
A等于________.
16.已知锐角A的正弦sin
A是一元二次方程2x2-7x+3=0的根,则sin
A=________.
17.数y=ax2﹣2ax+m(a>0)的图象过点(2,0),那么使函数值y<0成立的x的取值范围是
.
18.如右图,AB是⊙O的直径,点C、D在⊙O上,若∠ACD=25°,则∠BOD的度数为
.
19.如下图,PA、PB切⊙O于A、B,点C在上,DE切⊙O于C交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是
.
(第19图题)
(第20图题)
20.如上图,△ABC中,D在BC上,F是AD的中点,连CF并延长交AB于E,已知=,则等于
.
三.解答题(满分60分)
21.(5分)先化简,再求值:,其中
22.(7分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点,A(5,2),B(5,5),C(1,1)均在格点上,
将△ABC向左平移五个单位,单位得到△ABC,并求出点A坐标,
画出三角形,△ABC绕点C顺时针旋转90度后得到的△ABC并写出A的坐标.
在(2)的条件下,求△ABC在旋转过程中扫过的面积,(结果保留π)
23.(7分)已知二次函数的图象如图所示,它与轴的一个交点坐标为,与轴的交点坐标为.
(1)求此二次函数的表达式,并用配方法求顶点的坐标;
(2)直接写出当函数值时,自变量的取值范围.
24.(8分)
如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.
25(7分)如图,一次函数的图象与反比例函数的图象交于,两点,
求一次函数和反比例函数的表达式;
求的面积.
26(8分)一如图,海上有一灯塔P,在它周围3海里处有暗礁,一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在北偏东60°方向上,继续行驶20分钟后,到达B处又测得灯塔P在北偏东45°方向上,问客轮不改变方向继续前进有无触礁危险?
27.(8分)如图,已知在⊙O中,AB是⊙O的直径,AC=8,BC=6.
(1)求⊙O的面积;
(2)若D为⊙O上一点,且△ABD为等腰三角形,求CD的长.
28(10分)二如图,抛物线经过、、三点.
求抛物线的解析式;
如图①,在抛物线的对称轴上是否存在点,使得四边形的周长最小?若存在,求出四边形周长的最小值;若不存在,请说明理由.
如图②,点是线段上一动点,连接,在线段上是否存在这样的点,使为等腰三角形且为直角三角形?若存在,求点的坐标;若不存在,请说明理由.
密山市2020—2021学年第一学期期末质量检测
九年级数学答案
一.ACDBC
AADBD20.解:作DG∥CE,如图∵DG∥CE,∴==,设BG=2x,则GE=3x,∵EF∥DG,∴==1,∴AE=EG=3x,∴==.故答案为:.
二.11.(4.-3)
12.2021
13.8
14.5
15
16.
17.0
20.(20.解:作DG∥CE,如图∵DG∥CE,∴==,设BG=2x,则GE=3x,∵EF∥DG,∴==1,∴AE=EG=3x,∴==.故答案为:)
21.原式= --3分 代入,原式=--2分
22
(1)A(0.2)--2分(2)A(-3.-3)--2分
-----3分
23解:(1)由二次函数的图象经过和两点,
得,
解这个方程组,得
,
抛物线的解析式为,
由于,
则抛物线的顶点坐标为.--4分(2)令,得.
解这个方程,得,.
∴此二次函数的图象与轴的另一个交点的坐标为.
当时,.----3分
24.(1)证明:∵四边形EFMN是正方形,
∴EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴△AEF∽△ABC.---3分
(2)解:设正方形EFMN的边长为x.
∵△AEF∽△ABC,AD⊥BC,
∴=,
∴=,
∴x=8,
∴正方形的边长为8cm---5分
25解:∵点在的图象上,
∴,
∴反比例函数为,
又∵在的图象上,
∴,解得,
∴,
∵和都在直线上,
∴,解得,
∴一次函数解析式为;----4分
设直线与轴交于点,如图,
当时,,解得,则,
∴.---3分
26.解:过P作PC⊥AB于C点,如图,
(第24题)
据题意知AB=9×=3,--1分
∠PAB=90°-60°=30°,[]
∠PBC=90°-45°=45°,∠PCB=90°,∴PC=BC.--2分
在Rt△APC中,tan
30°===,--2分
即=,∴PC=海里>3海里,
∴客轮不改变方向继续前进无触礁危 --- 3分
27.解:(1)∵AB是⊙O的直径,
∴∠ACB=90°.
∴AC=8,BC=6,
∴AB=10.
∴⊙O的面积=π×52=25π;--2分
(2)作直径DD′⊥AB,BH⊥CD于H,如图,则=,
∴AD=BD,∠ACD=∠BCD=45°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴△ADB为等腰直角三角形,
∴DB=AB=5,
易得△BCH为等腰直角三角形,
∴CH=BH=BC=3,
在Rt△BDH中,DH==4,
∴CD=CH+DH=3+4=7,----4分
∵DD′是⊙O的直径,
∴∠DCD′=90°,
∴CD′==,
综上所述,CD的长为或7.
------2分
28.解:由已知得解得.
所以,抛物线的解析式为.---3分
∵、关于对称轴对称,如图,连接,
∴与对称轴的交点即为所求的点,此时,
∴四边形的周长最小值为:,
∵、、,
∴,,,
∴;
∴在抛物线的对称轴上存在点,使得四边形的周长最小,四边形周长的最小值为.----3分
∵、,
∴直线的解析式为,
①当时,如图,设,
∵,
∴只能,
∵轴,
∴,
∴,即,解得,
代入得,,解得,
∴;
②当时,如图,
∵,
∴只能,
设,
∴,
∵,,
∴,
∴,解得,
作,
∴,即,
∴,,
∴,
∴,
综上,在线段上存在这样的点,使为等腰三角形且为直角三角形,点的坐标为或.
----4分
九年级数学
同课章节目录
