2021-2022学年苏科新版八年级上册数学《第3章 勾股定理》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年苏科新版八年级上册数学《第3章 勾股定理》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 339.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览



文档简介
2021-2022学年苏科新版八年级上册数学《第3章
勾股定理》单元测试卷
一.选择题
1.如图,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是( )
A.∠1
B.∠2
C.∠B
D.∠1、∠2和∠B
2.如图,AB∥DF,AC⊥CE于C,BC与DF交于点E,若∠A=20°,则∠CEF等于( )
A.110°
B.100°
C.80°
D.70°
3.在直角三角形中,两条直角边的长分别为12和5,则斜边上的中线长是( )
A.6.5
B.8.5
C.13
D.
4.下列四组线段中,可以构成直角三角形的是( )
A.1,,
B.2,3,4
C.1,2,3
D.4,5,6
5.下列四组数据中,不能作为直角三角形的三边长的是( )
A.7,24,25
B.6,8,10
C.9,12,15
D.3,4,6
6.如图,在直角三角形ABC中,AC≠AB,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )
A.3个
B.4个
C.5个
D.6个
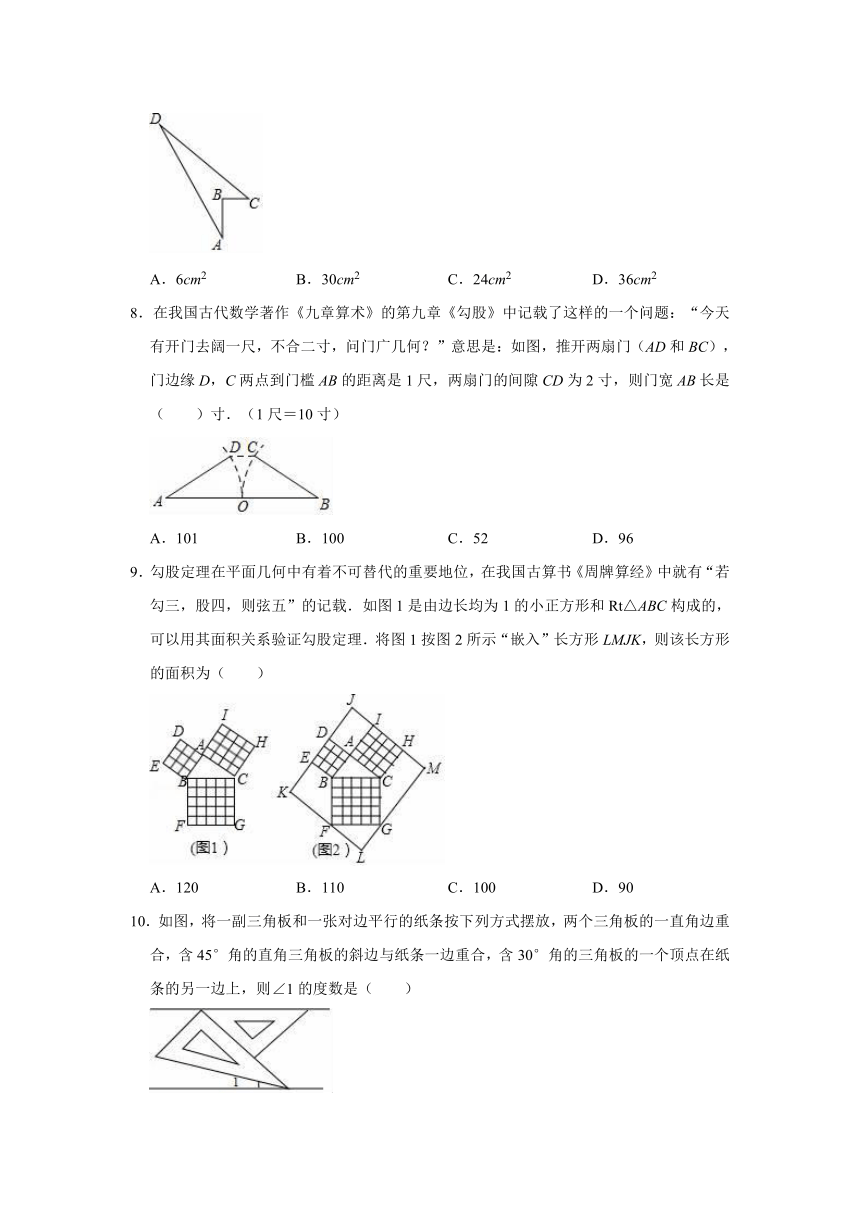
7.如图,四边形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( )
A.6cm2
B.30cm2
C.24cm2
D.36cm2
8.在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样的一个问题:“今天有开门去阔一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB长是( )寸.(1尺=10寸)
A.101
B.100
C.52
D.96
9.勾股定理在平面几何中有着不可替代的重要地位,在我国古算书《周牌算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理.将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( )
A.120
B.110
C.100
D.90
10.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.10°
B.15°
C.20°
D.25°
二.填空题
11.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有
(填序号)
12.已知:△ABC中,AB=4cm,AC=3cm,BC=5cm,则△ABC的面积是
cm2.
13.观察以下几组勾股数,并寻找规律:请你写出有以上规律的第⑤组勾股数:
.
①3,4,5;②5,12,13;③7,24,25;④9,40,41.
14.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是
.
15.已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连接ME、MD、ED.设AB=4,∠DBE=30°,则△EDM的面积为
.
16.已知△ABC的三边长分别为1,,2,则△ABC是
三角形.
17.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了
步路(假设2步为1米),却踩伤了花草.
18.等腰△ABC的腰长AB为5,底边BC的长为6,则底边上的高长为
.
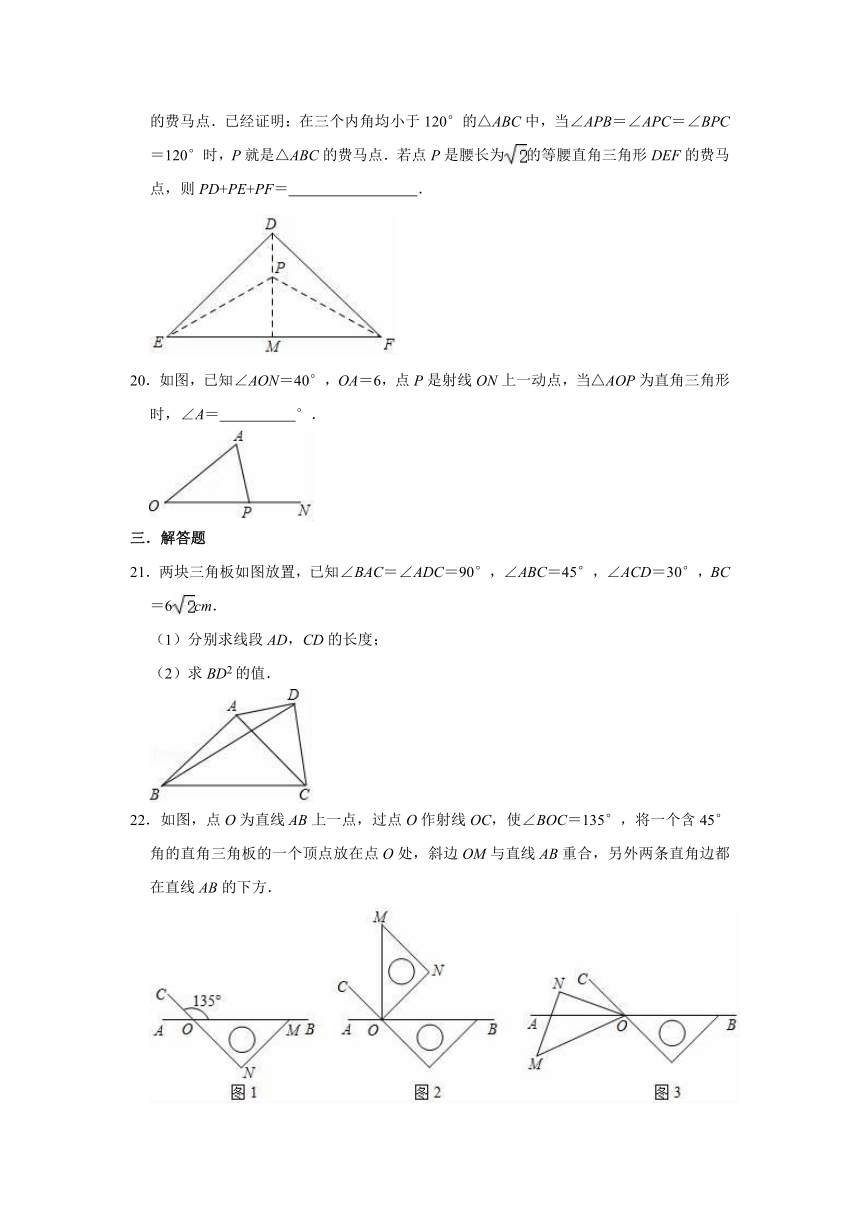
19.如果点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点.已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为的等腰直角三角形DEF的费马点,则PD+PE+PF=
.
20.如图,已知∠AON=40°,OA=6,点P是射线ON上一动点,当△AOP为直角三角形时,∠A=
°.
三.解答题
21.两块三角板如图放置,已知∠BAC=∠ADC=90°,∠ABC=45°,∠ACD=30°,BC=6cm.
(1)分别求线段AD,CD的长度;
(2)求BD2的值.
22.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角板的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.
(1)将图1中的三角板绕着点O逆时针旋转90°,如图2所示,此时∠BOM=
;在图2中,OM是否平分∠CON?请说明理由;
(2)接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒4.5°的速度沿逆时针方向旋转一周,在旋转的过程中,当旋转到第
秒时,∠COM与∠CON互补.
23.如图,在△ABC中,∠ACB=90°,AC=m,BC=n,m>n,点P是边AB上一点,连接CP,将△ACP沿CP翻折得到△QCP.
(1)若m=4,n=3,且PQ⊥AB,求BP的长;
(2)连接BQ,若四边形BCPQ是平行四边形,求m与n之间的关系式.
24.如图所示,在△ABC中,已知AD⊥BC,∠B=64°,∠C=56°,
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数.
25.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题:
(1)试说明a2+b2=c2;
(2)如果大正方形的面积是10,小正方形的面积是2,求(a+b)2的值.
26.如图所示,在△ABC中,CD⊥AB于D,AC=4,BC=3,CD=
(1)求AD的长;
(2)求证:△ABC是直角三角形.
27.如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,斜边AB与y轴交于点C.
(1)若∠A=∠AOC,求证:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,且∠DOB=∠EOB,∠OAE=∠OEA,求∠A度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,当△ABO绕O点旋转时(斜边AB与y轴正半轴始终相交于点C),在(2)的条件下,试问∠P的度数是否发生改变?若不变,请求其度数;若改变,请说明理由.
参考答案与试题解析
一.选择题
1.解:∵∠ACB=90°,即∠1+∠2=90°,
又∵直角△ACD中,∠A+∠1=90°,
∴∠A=∠2.
故选:B.
2.解:∵AC⊥BC于C,
∴△ABC是直角三角形,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣20°﹣90°=70°,
∴∠ABC=∠1=70°,
∵AB∥DF,
∴∠1+∠CEF=180°,
即∠CEF=180°﹣∠1=180°﹣70°=110°.
故选:A.
3.解:如图,在△ABC中,∠C=90°,AC=12,BC=5,
则根据勾股定理知,AB==13,
∵CD为斜边AB上的中线,
∴CD=AB=6.5.
故选:A.
4.解:A、∵12+()2=()2,
∴以1、、为边组成的三角形是直角三角形,故本选项正确;
B、∵22+32≠42,
∴以2、3、4为边组成的三角形不是直角三角形,故本选项错误;
C、∵12+22≠32,
∴以1、2、3为边组成的三角形不是直角三角形,故本选项错误;
D、∵42+52≠62,
∴以4、5、6为边组成的三角形不是直角三角形,故本选项错误;
故选:A.
5.解:A、72+242=252,符合勾股定理的逆定理,故能作为直角三角形的三边长;
B、62+82=102,符合勾股定理的逆定理,故能作为直角三角形的三边长;
C、92+122=152,符合勾股定理的逆定理,故能作为直角三角形的三边长;
D、32+42≠62,不符合勾股定理的逆定理,故不能作为直角三角形的三边长.
故选:D.
6.解:∵AD是斜边BC上的高,DE⊥AC,DF⊥AB,
∴∠C+∠B=90°,∠BDF+∠B=90°,∠BAD+∠B=90°,
∴∠C=∠BDF=∠BAD,
∵∠DAC+∠C=90°,∠DAC+∠ADE=90°,
∴∠C=∠ADE,
∴图中与∠C(除之C外)相等的角的个数是3,
故选:A.
7.解:连接AC,
∵∠ABC=90°,AB=4cm,BC=3cm,
∴AC=5cm,
∵CD=12cm,DA=13cm,
AC2+CD2=52+122=169=132=DA2,
∴△ADC为直角三角形,
∴S四边形ABCD=S△ACD﹣S△ABC
=AC×CD﹣AB×BC
=×5×12﹣×4×3
=30﹣6
=24(cm2).
故四边形ABCD的面积为24cm2.
故选:C.
8.解:过点D作DE⊥AB,垂足为E,
设单门的宽度AO是x寸,则AE=x﹣1,DE=10寸,
根据勾股定理,得:AD2=DE2+AE2,
则x2=102+(x﹣1)2,
解得:x=50.5,
故AB=101寸,
故选:A.
9.解:延长AB交KF于点O,延长AC交GM于点P,如图所示:
则四边形OALP是矩形.
∵∠CBF=90°,
∴∠ABC+∠OBF=90°,
又∵Rt△ABC中,∠ABC+∠ACB=90°,
∴∠OBF=∠ACB,
在△OBF和△ACB中,
,
∴△OBF≌△ACB(AAS),
∴AC=OB,
同理:△ACB≌△PGC,
∴PC=AB,
∴OA=AP,
∴矩形AOLP是正方形,边长AO=AB+AC=3+4=7,
∴KL=3+7=10,LM=4+7=11,
∴长方形KLMJ的面积为10×11=110.
故选:B.
10.解:∵AB∥CD,
∴∠BCD=∠ABC=45°,
∴∠1=∠BCD﹣∠BCE=45°﹣30°=15°.
故选:B.
二.填空题
11.解:①∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴2∠C=180°,∠C=90°,则该三角形是直角三角形;
②∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,∴∠C=90°,则该三角形是直角三角形;
③∠A=90°﹣∠B,则∠A+∠B=90°,∠C=90°.则该三角形是直角三角形;
④∠A=∠B=∠C,则该三角形是等边三角形.
故能确定△ABC是直角三角形的条件有①②③.
12.解:
∵AB=4cm,AC=3cm,BC=5cm,
∴AB2+AC2=25cm2,BC2=25cm2,
∴AB2+AC2=BC2,
∴∠A=90°,
∴△ABC的面积是AC×AB=×3cm×4cm=6cm2,
故答案为:6.
13.解:∵①3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,
②5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,
③7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,…,
∴第n组勾股数为:
a=2n+1,b=2n(n+1),c=2n(n+1)+1,
∴第⑤组勾股数为a=2×5+1=11,b=2×5×(5+1)=60,c=2×5×(5+1)+1=61,即11,60,61.
故答案为:11,60,61.
14.解:∵勾a=6,弦c=10,
∴股==8,
∴小正方形的边长=8﹣6=2,
∴小正方形的面积=22=4
故答案是:4
15.解:∵在△ABC中,AD⊥BC,BE⊥AC,
∴△ABE,△ADB是直角三角形,
∴EM,DM分别是它们斜边上的中线,
∴EM=DM=AB,
∵ME=AB=MA,
∴∠MAE=∠MEA,
∴∠BME=2∠MAE,
同理,MD=AB=MA,
∴∠MAD=∠MDA,
∴∠BMD=2∠MAD,
∴∠EMD=∠BME﹣∠BMD=2∠MAE﹣2∠MAD=2∠DAC=60°,
所以△DEM是边长为2的正三角形,所以S△DEM=.
故答案为:.
16.解:∵12+()2=22,
∴△ABC是直角三角形.
故答案为:直角.
17.解:由勾股定理,得
路长==5,
少走(3+4﹣5)×2=4步,
故答案为:4.
18.解:过A作AD⊥BC于D,
则线段AD是等腰△ABC底边BC上的高,
∵AB=AC,BC=6,AD⊥BC,
∴BD=DC=3,∠AB=90°,
由勾股定理得:AD===4,
故答案为:4.
19.解:如图:过点D作DM⊥EF于点M,在△BDE内部过E、F分别作∠MEP=∠MFP=30°,则∠EPF=∠FPD=∠EPD=120°,点P就是费马点,
在等腰Rt△DEF中,DE=DF=,DM⊥EF,
∴EF=DE=2
∴EM=DM=1,
故cos30°=,
解得:PE=,则PM=,
故DP=1﹣,同法可得PF=
则PD+PE+PF=2×+1﹣=+1.
故答案为+1.
20.解:当AP⊥ON时,∠APO=90°,则∠A=50°,
当PA⊥OA时,∠A=90°,
即当△AOP为直角三角形时,∠A=50或90°.
故答案为:50或90.
三.解答题
21.解:(1)在Rt△ABC中,∠ABC=45°,
∴AB=AC=BC=6(cm),
在Rt△ADC中,∠ACD=30°,
∴AD=AC=3(cm),
由勾股定理得,CD==3(cm);
(2)过点B作BE⊥AD交DA的延长线于E,
由题意得,∠BAE=180°﹣90°﹣60°=30°,
∴BE=AB=3(cm),
由勾股定理得,AE==3(cm),
∴DE=AE+AD=(3+3)cm,
∴BD2=BE2+DE2=32+(3+3)2=(45+18)cm.
22.解:(1)如图2,∠BOM=90°,
OM平分∠CON.理由如下:
∵∠BOC=135°,
∴∠MOC=135°﹣90°=45°,
而∠MON=45°,
∴∠MOC=∠MON;
故答案为90°;
(2)∠AOM=∠CON.
理由如下:如图3,
∵∠MON=45°,
∴∠AOM=45°﹣∠AON,
∵∠AOC=45°,
∴∠NOC=45°﹣∠AON,
∴∠AOM=∠CON;
(3)如图2,OM、ON都在OC右侧,∠COM+∠CON=2∠COM+45°=180°,
∴∠COM=67.5°,
∴∠CON=67.5+45=112.5°,
∴45°+∠BON=180°﹣112.5=67.5°,
如图3,OM、ON都在OC左侧,∠COM+∠CON=2∠CON+45°=180°,
∴∠CON=67.5°,
∴∠BOM=67.5+45=112.5°,
∴∠BOC+∠COM=135+112.5=247.5°,
∴在旋转的过程中,∠COM与∠CON互补,则ON旋转67.5°或247.5°,
∴=15或=55,
故答案为:15或55.
23.解:(1)如图,作CH⊥AB于H.
由翻折的性质可知:∠APC=∠QPC,
∵PQ⊥PA,
∴∠APQ=90°,
∴∠APC=∠QPC=135°,
∴∠BPC+∠QPB=135°,
∵∠QPB=90°,
∴∠BPC=45°,
∵CH⊥AB,
∴CH=PH,
在Rt△ABC中,AB===5,
∵?AB?CH=?AC?BC,
∴CH=,BH==,
∴PB=PH+BH=+=.
(2)如图2中,连接BQ.
由翻折不变性可知:PA=PQ,∠QPC=∠APC,
∵四边形BCPQ是平行四边形,
∴PQ=BC=PA=n,PQ∥BC,
∴∠QPC+∠PCB=180°,
∵∠BPC+∠APC=180°,
∴∠PCB=∠BPC,
∴PB=BC=n,
∴AP=PB=n,AB=2n,
在Rt△ABC中,则有(2n)2=m2+n2,
∴m2=3n2,
∵m>0.n>0,
∴m=n.
24.解:(1)∵AD⊥BC,
①∴在Rt△BAD中,∠BAD+∠B=90°,
又∵∠B=64°,
∴∠BAD=26°;
②∴在Rt△DAC中,
∠DAC+∠C=90°,
又∵∠C=56°,
∴∠DAC=34°;
(2)∵AD⊥BC,DE平分∠ADB,
∴∠BDE=45°;
在△BED中,∠B=64°,
∴∠B+∠BDE=109°;
∵∠AED=∠B+∠BDE,
∴∠AED=109°.
25.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2.;
(2)由图可知,(b﹣a)2=2,4×ab=10﹣2=8,
∴2ab=8,
∴(a+b)2=(b﹣a)2+4ab=2+2×8=18.
26.解:(1)∵CD⊥AB,
∴∠ADC=90°,
∴AD===;
(2)证明:由上题知AD=,
同理可得BD=,
∴AB=AD+BD=5,
∵32+42=52,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
27.解:(1)∵△AOB是直角三角形,
∴∠A+∠B=90°,∠AOC+∠BOC=90°.
∵∠A=∠AOC,
∴∠B=∠BOC;
(2)∵∠A+∠ABO=90°,∠DOB+∠ABO=90°,
∴∠A=∠DOB,即∠DOB=∠EOB=∠OAE=∠OEA.
∵∠DOB+∠EOB+∠OEA=90°,
∴∠DOB=30°,
∴∠A=30°;
(3)∠P的度数不变,∠P=30°,
∵∠AOM=90°﹣∠AOC,∠BCO=∠A+∠AOC,
∵OF平分∠AOM,CP平分∠BCO,
∴∠FOM=∠AOM=(90°﹣∠AOC)=45°﹣∠AOC,∠PCO=∠BCO=(∠A+∠AOC)=∠A+∠AOC.
∴∠P=180°﹣(∠PCO+∠FOM+90°)
=45°﹣∠A
=30°.
勾股定理》单元测试卷
一.选择题
1.如图,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是( )
A.∠1
B.∠2
C.∠B
D.∠1、∠2和∠B
2.如图,AB∥DF,AC⊥CE于C,BC与DF交于点E,若∠A=20°,则∠CEF等于( )
A.110°
B.100°
C.80°
D.70°
3.在直角三角形中,两条直角边的长分别为12和5,则斜边上的中线长是( )
A.6.5
B.8.5
C.13
D.
4.下列四组线段中,可以构成直角三角形的是( )
A.1,,
B.2,3,4
C.1,2,3
D.4,5,6
5.下列四组数据中,不能作为直角三角形的三边长的是( )
A.7,24,25
B.6,8,10
C.9,12,15
D.3,4,6
6.如图,在直角三角形ABC中,AC≠AB,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )
A.3个
B.4个
C.5个
D.6个
7.如图,四边形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( )
A.6cm2
B.30cm2
C.24cm2
D.36cm2
8.在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样的一个问题:“今天有开门去阔一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB长是( )寸.(1尺=10寸)
A.101
B.100
C.52
D.96
9.勾股定理在平面几何中有着不可替代的重要地位,在我国古算书《周牌算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理.将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( )
A.120
B.110
C.100
D.90
10.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.10°
B.15°
C.20°
D.25°
二.填空题
11.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有
(填序号)
12.已知:△ABC中,AB=4cm,AC=3cm,BC=5cm,则△ABC的面积是
cm2.
13.观察以下几组勾股数,并寻找规律:请你写出有以上规律的第⑤组勾股数:
.
①3,4,5;②5,12,13;③7,24,25;④9,40,41.
14.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是
.
15.已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连接ME、MD、ED.设AB=4,∠DBE=30°,则△EDM的面积为
.
16.已知△ABC的三边长分别为1,,2,则△ABC是
三角形.
17.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了
步路(假设2步为1米),却踩伤了花草.
18.等腰△ABC的腰长AB为5,底边BC的长为6,则底边上的高长为
.
19.如果点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点.已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为的等腰直角三角形DEF的费马点,则PD+PE+PF=
.
20.如图,已知∠AON=40°,OA=6,点P是射线ON上一动点,当△AOP为直角三角形时,∠A=
°.
三.解答题
21.两块三角板如图放置,已知∠BAC=∠ADC=90°,∠ABC=45°,∠ACD=30°,BC=6cm.
(1)分别求线段AD,CD的长度;
(2)求BD2的值.
22.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角板的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.
(1)将图1中的三角板绕着点O逆时针旋转90°,如图2所示,此时∠BOM=
;在图2中,OM是否平分∠CON?请说明理由;
(2)接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒4.5°的速度沿逆时针方向旋转一周,在旋转的过程中,当旋转到第
秒时,∠COM与∠CON互补.
23.如图,在△ABC中,∠ACB=90°,AC=m,BC=n,m>n,点P是边AB上一点,连接CP,将△ACP沿CP翻折得到△QCP.
(1)若m=4,n=3,且PQ⊥AB,求BP的长;
(2)连接BQ,若四边形BCPQ是平行四边形,求m与n之间的关系式.
24.如图所示,在△ABC中,已知AD⊥BC,∠B=64°,∠C=56°,
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数.
25.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题:
(1)试说明a2+b2=c2;
(2)如果大正方形的面积是10,小正方形的面积是2,求(a+b)2的值.
26.如图所示,在△ABC中,CD⊥AB于D,AC=4,BC=3,CD=
(1)求AD的长;
(2)求证:△ABC是直角三角形.
27.如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,斜边AB与y轴交于点C.
(1)若∠A=∠AOC,求证:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,且∠DOB=∠EOB,∠OAE=∠OEA,求∠A度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,当△ABO绕O点旋转时(斜边AB与y轴正半轴始终相交于点C),在(2)的条件下,试问∠P的度数是否发生改变?若不变,请求其度数;若改变,请说明理由.
参考答案与试题解析
一.选择题
1.解:∵∠ACB=90°,即∠1+∠2=90°,
又∵直角△ACD中,∠A+∠1=90°,
∴∠A=∠2.
故选:B.
2.解:∵AC⊥BC于C,
∴△ABC是直角三角形,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣20°﹣90°=70°,
∴∠ABC=∠1=70°,
∵AB∥DF,
∴∠1+∠CEF=180°,
即∠CEF=180°﹣∠1=180°﹣70°=110°.
故选:A.
3.解:如图,在△ABC中,∠C=90°,AC=12,BC=5,
则根据勾股定理知,AB==13,
∵CD为斜边AB上的中线,
∴CD=AB=6.5.
故选:A.
4.解:A、∵12+()2=()2,
∴以1、、为边组成的三角形是直角三角形,故本选项正确;
B、∵22+32≠42,
∴以2、3、4为边组成的三角形不是直角三角形,故本选项错误;
C、∵12+22≠32,
∴以1、2、3为边组成的三角形不是直角三角形,故本选项错误;
D、∵42+52≠62,
∴以4、5、6为边组成的三角形不是直角三角形,故本选项错误;
故选:A.
5.解:A、72+242=252,符合勾股定理的逆定理,故能作为直角三角形的三边长;
B、62+82=102,符合勾股定理的逆定理,故能作为直角三角形的三边长;
C、92+122=152,符合勾股定理的逆定理,故能作为直角三角形的三边长;
D、32+42≠62,不符合勾股定理的逆定理,故不能作为直角三角形的三边长.
故选:D.
6.解:∵AD是斜边BC上的高,DE⊥AC,DF⊥AB,
∴∠C+∠B=90°,∠BDF+∠B=90°,∠BAD+∠B=90°,
∴∠C=∠BDF=∠BAD,
∵∠DAC+∠C=90°,∠DAC+∠ADE=90°,
∴∠C=∠ADE,
∴图中与∠C(除之C外)相等的角的个数是3,
故选:A.
7.解:连接AC,
∵∠ABC=90°,AB=4cm,BC=3cm,
∴AC=5cm,
∵CD=12cm,DA=13cm,
AC2+CD2=52+122=169=132=DA2,
∴△ADC为直角三角形,
∴S四边形ABCD=S△ACD﹣S△ABC
=AC×CD﹣AB×BC
=×5×12﹣×4×3
=30﹣6
=24(cm2).
故四边形ABCD的面积为24cm2.
故选:C.
8.解:过点D作DE⊥AB,垂足为E,
设单门的宽度AO是x寸,则AE=x﹣1,DE=10寸,
根据勾股定理,得:AD2=DE2+AE2,
则x2=102+(x﹣1)2,
解得:x=50.5,
故AB=101寸,
故选:A.
9.解:延长AB交KF于点O,延长AC交GM于点P,如图所示:
则四边形OALP是矩形.
∵∠CBF=90°,
∴∠ABC+∠OBF=90°,
又∵Rt△ABC中,∠ABC+∠ACB=90°,
∴∠OBF=∠ACB,
在△OBF和△ACB中,
,
∴△OBF≌△ACB(AAS),
∴AC=OB,
同理:△ACB≌△PGC,
∴PC=AB,
∴OA=AP,
∴矩形AOLP是正方形,边长AO=AB+AC=3+4=7,
∴KL=3+7=10,LM=4+7=11,
∴长方形KLMJ的面积为10×11=110.
故选:B.
10.解:∵AB∥CD,
∴∠BCD=∠ABC=45°,
∴∠1=∠BCD﹣∠BCE=45°﹣30°=15°.
故选:B.
二.填空题
11.解:①∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴2∠C=180°,∠C=90°,则该三角形是直角三角形;
②∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,∴∠C=90°,则该三角形是直角三角形;
③∠A=90°﹣∠B,则∠A+∠B=90°,∠C=90°.则该三角形是直角三角形;
④∠A=∠B=∠C,则该三角形是等边三角形.
故能确定△ABC是直角三角形的条件有①②③.
12.解:
∵AB=4cm,AC=3cm,BC=5cm,
∴AB2+AC2=25cm2,BC2=25cm2,
∴AB2+AC2=BC2,
∴∠A=90°,
∴△ABC的面积是AC×AB=×3cm×4cm=6cm2,
故答案为:6.
13.解:∵①3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,
②5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,
③7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,…,
∴第n组勾股数为:
a=2n+1,b=2n(n+1),c=2n(n+1)+1,
∴第⑤组勾股数为a=2×5+1=11,b=2×5×(5+1)=60,c=2×5×(5+1)+1=61,即11,60,61.
故答案为:11,60,61.
14.解:∵勾a=6,弦c=10,
∴股==8,
∴小正方形的边长=8﹣6=2,
∴小正方形的面积=22=4
故答案是:4
15.解:∵在△ABC中,AD⊥BC,BE⊥AC,
∴△ABE,△ADB是直角三角形,
∴EM,DM分别是它们斜边上的中线,
∴EM=DM=AB,
∵ME=AB=MA,
∴∠MAE=∠MEA,
∴∠BME=2∠MAE,
同理,MD=AB=MA,
∴∠MAD=∠MDA,
∴∠BMD=2∠MAD,
∴∠EMD=∠BME﹣∠BMD=2∠MAE﹣2∠MAD=2∠DAC=60°,
所以△DEM是边长为2的正三角形,所以S△DEM=.
故答案为:.
16.解:∵12+()2=22,
∴△ABC是直角三角形.
故答案为:直角.
17.解:由勾股定理,得
路长==5,
少走(3+4﹣5)×2=4步,
故答案为:4.
18.解:过A作AD⊥BC于D,
则线段AD是等腰△ABC底边BC上的高,
∵AB=AC,BC=6,AD⊥BC,
∴BD=DC=3,∠AB=90°,
由勾股定理得:AD===4,
故答案为:4.
19.解:如图:过点D作DM⊥EF于点M,在△BDE内部过E、F分别作∠MEP=∠MFP=30°,则∠EPF=∠FPD=∠EPD=120°,点P就是费马点,
在等腰Rt△DEF中,DE=DF=,DM⊥EF,
∴EF=DE=2
∴EM=DM=1,
故cos30°=,
解得:PE=,则PM=,
故DP=1﹣,同法可得PF=
则PD+PE+PF=2×+1﹣=+1.
故答案为+1.
20.解:当AP⊥ON时,∠APO=90°,则∠A=50°,
当PA⊥OA时,∠A=90°,
即当△AOP为直角三角形时,∠A=50或90°.
故答案为:50或90.
三.解答题
21.解:(1)在Rt△ABC中,∠ABC=45°,
∴AB=AC=BC=6(cm),
在Rt△ADC中,∠ACD=30°,
∴AD=AC=3(cm),
由勾股定理得,CD==3(cm);
(2)过点B作BE⊥AD交DA的延长线于E,
由题意得,∠BAE=180°﹣90°﹣60°=30°,
∴BE=AB=3(cm),
由勾股定理得,AE==3(cm),
∴DE=AE+AD=(3+3)cm,
∴BD2=BE2+DE2=32+(3+3)2=(45+18)cm.
22.解:(1)如图2,∠BOM=90°,
OM平分∠CON.理由如下:
∵∠BOC=135°,
∴∠MOC=135°﹣90°=45°,
而∠MON=45°,
∴∠MOC=∠MON;
故答案为90°;
(2)∠AOM=∠CON.
理由如下:如图3,
∵∠MON=45°,
∴∠AOM=45°﹣∠AON,
∵∠AOC=45°,
∴∠NOC=45°﹣∠AON,
∴∠AOM=∠CON;
(3)如图2,OM、ON都在OC右侧,∠COM+∠CON=2∠COM+45°=180°,
∴∠COM=67.5°,
∴∠CON=67.5+45=112.5°,
∴45°+∠BON=180°﹣112.5=67.5°,
如图3,OM、ON都在OC左侧,∠COM+∠CON=2∠CON+45°=180°,
∴∠CON=67.5°,
∴∠BOM=67.5+45=112.5°,
∴∠BOC+∠COM=135+112.5=247.5°,
∴在旋转的过程中,∠COM与∠CON互补,则ON旋转67.5°或247.5°,
∴=15或=55,
故答案为:15或55.
23.解:(1)如图,作CH⊥AB于H.
由翻折的性质可知:∠APC=∠QPC,
∵PQ⊥PA,
∴∠APQ=90°,
∴∠APC=∠QPC=135°,
∴∠BPC+∠QPB=135°,
∵∠QPB=90°,
∴∠BPC=45°,
∵CH⊥AB,
∴CH=PH,
在Rt△ABC中,AB===5,
∵?AB?CH=?AC?BC,
∴CH=,BH==,
∴PB=PH+BH=+=.
(2)如图2中,连接BQ.
由翻折不变性可知:PA=PQ,∠QPC=∠APC,
∵四边形BCPQ是平行四边形,
∴PQ=BC=PA=n,PQ∥BC,
∴∠QPC+∠PCB=180°,
∵∠BPC+∠APC=180°,
∴∠PCB=∠BPC,
∴PB=BC=n,
∴AP=PB=n,AB=2n,
在Rt△ABC中,则有(2n)2=m2+n2,
∴m2=3n2,
∵m>0.n>0,
∴m=n.
24.解:(1)∵AD⊥BC,
①∴在Rt△BAD中,∠BAD+∠B=90°,
又∵∠B=64°,
∴∠BAD=26°;
②∴在Rt△DAC中,
∠DAC+∠C=90°,
又∵∠C=56°,
∴∠DAC=34°;
(2)∵AD⊥BC,DE平分∠ADB,
∴∠BDE=45°;
在△BED中,∠B=64°,
∴∠B+∠BDE=109°;
∵∠AED=∠B+∠BDE,
∴∠AED=109°.
25.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2.;
(2)由图可知,(b﹣a)2=2,4×ab=10﹣2=8,
∴2ab=8,
∴(a+b)2=(b﹣a)2+4ab=2+2×8=18.
26.解:(1)∵CD⊥AB,
∴∠ADC=90°,
∴AD===;
(2)证明:由上题知AD=,
同理可得BD=,
∴AB=AD+BD=5,
∵32+42=52,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
27.解:(1)∵△AOB是直角三角形,
∴∠A+∠B=90°,∠AOC+∠BOC=90°.
∵∠A=∠AOC,
∴∠B=∠BOC;
(2)∵∠A+∠ABO=90°,∠DOB+∠ABO=90°,
∴∠A=∠DOB,即∠DOB=∠EOB=∠OAE=∠OEA.
∵∠DOB+∠EOB+∠OEA=90°,
∴∠DOB=30°,
∴∠A=30°;
(3)∠P的度数不变,∠P=30°,
∵∠AOM=90°﹣∠AOC,∠BCO=∠A+∠AOC,
∵OF平分∠AOM,CP平分∠BCO,
∴∠FOM=∠AOM=(90°﹣∠AOC)=45°﹣∠AOC,∠PCO=∠BCO=(∠A+∠AOC)=∠A+∠AOC.
∴∠P=180°﹣(∠PCO+∠FOM+90°)
=45°﹣∠A
=30°.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
