北京市西城区育才高级中学2020-2021学年高二下学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 北京市西城区育才高级中学2020-2021学年高二下学期期中考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 19:34:54 | ||
图片预览




文档简介
2020-2021学年北京市西城区育才学校高二(下)期中数学试卷
一、选择题:本大题共10小题,每小题4分,共.40分.在每小题给出的四个选项中,只有一项是符合要求的.
1.(4分)在数列中,,且,则等于
A.8
B.6
C.9
D.7
2.(4分)函数的导数是
A.
B.
C.
D.
3.(4分)将一枚均匀硬币随机掷3次,恰好出现2次正面向上的概率为
A.
B.
C.
D.
4.(4分)曲线在点处的切线方程是
A.
B.
C.
D.
5.(4分)等差数列的首项,公差,如果、、成等比数列,那么等于
A.3
B.
C.2
D.
6.(4分)函数在
A.内是增函数
B.内是减函数
C.内是增函数,在其余区间内是减函数
D.内是减函数,在其余区间内是增函数
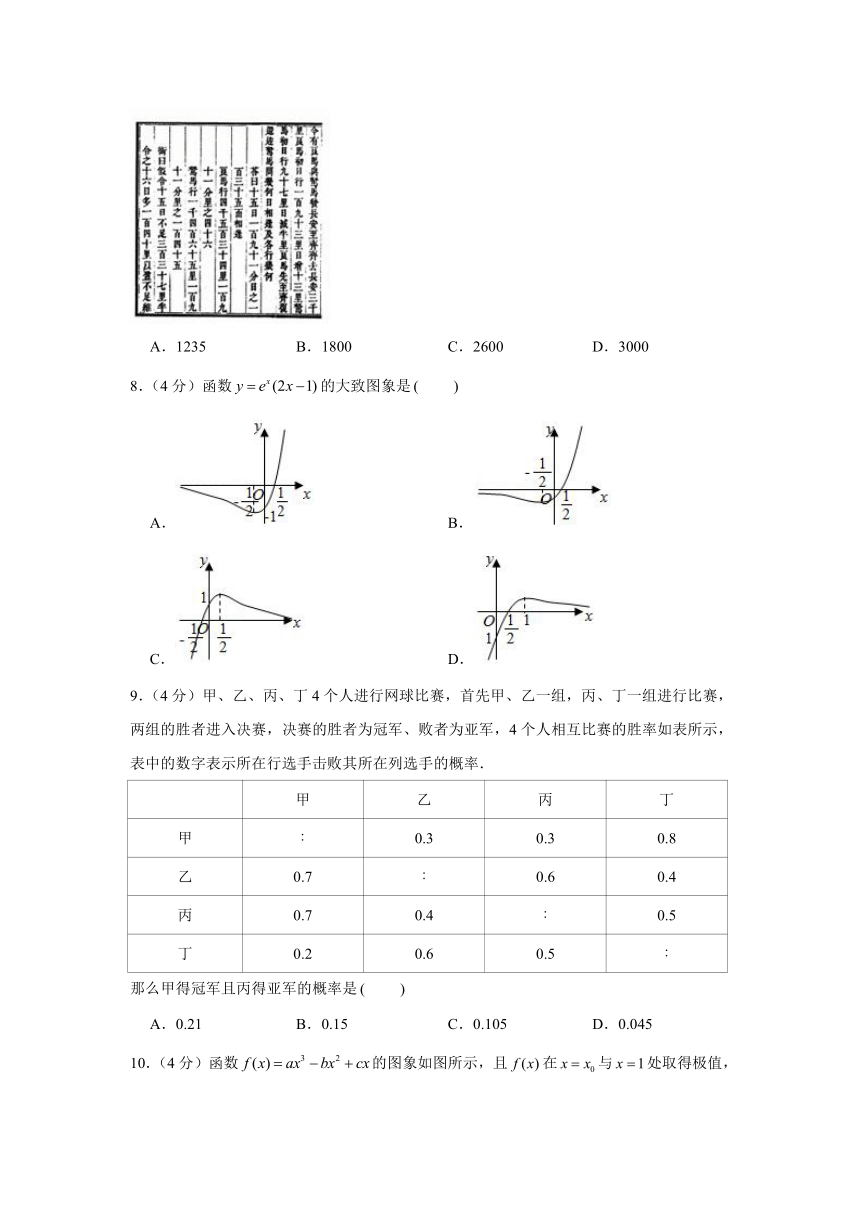
7.(4分)《九章算术》的盈不足章第19个问题中提到:“今有良马与驽马发长安,至齐.齐去长安三千里.良马初日行一百九十三里,日增一十三里.驽马初日行九十七里,日减半里”其大意为:“现在有良马和驽马同时从长安出发到齐去.已知长安和齐的距离是3000里.良马第一天行193里,之后每天比前一天多行13里.驽马第一天行97里,之后每天比前一天少行0.5里”试问前4天,良马和驽马共走过的路程之和的里数为
A.1235
B.1800
C.2600
D.3000
8.(4分)函数的大致图象是
A.
B.
C.
D.
9.(4分)甲、乙、丙、丁4个人进行网球比赛,首先甲、乙一组,丙、丁一组进行比赛,两组的胜者进入决赛,决赛的胜者为冠军、败者为亚军,4个人相互比赛的胜率如表所示,表中的数字表示所在行选手击败其所在列选手的概率.
甲
乙
丙
丁
甲
0.3
0.3
0.8
乙
0.7
0.6
0.4
丙
0.7
0.4
0.5
丁
0.2
0.6
0.5
那么甲得冠军且丙得亚军的概率是
A.0.21
B.0.15
C.0.105
D.0.045
10.(4分)函数的图象如图所示,且在与处取得极值,给出下列判断:
①;
②(1);
③函数在区间上是增函数.
其中正确的判断是
A.①③
B.②
C.②③
D.①②
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.
11.(5分)设是等差数列的前项和,若,则 .
12.(5分)已知函数,则(1) .
13.(5分)离散型随机变量的分布列为:
1
2
3
且,则 ; .
14.(5分)等比数列满足如下条件:①;②数列单调递增,试写出满足上述所有条件的一个数列的通项公式 .
15.(5分)研究函数的性质,完成下面两个问题:
①将(2),(3),(5)按从小到大排列为 ;
②若方程有两个不同的实根,则实数的取值范围是 .
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(13分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为与,且乙投球2次均未命中的概率为.
(Ⅰ)求甲投球2次,至少命中1次的概率;
(Ⅱ)若甲、乙两人各投球2次,求两人共命中3次的概率.
17.(14分)已知函数.
(Ⅰ)求函数的单调增区间和减区间;
(Ⅱ)当,时,求函数的最值和最值点.
18.(14分)已知数列中,,______,其中.
(Ⅰ)求数列的通项公式:
(Ⅱ)设,求证:数列是等比数列;
(Ⅲ)求数列的前项和.
从①前项和,②,③且,这三个条件中任选一个,补充在上面的问题中并作答.
19.(14分)流行性感冒多由病毒引起,据调查,空气月平均相对湿度过大或过小时,都有利于一些病毒繁殖和传播,科学测定,当空气月平均相对湿度大于或小于时,有利于病毒繁殖和传播.下表记录了某年甲、乙两个城市12个月的空气月平均相对湿度
第一季度
第二季度
第三季度
第四季度
1月
2月
3月
4月
5月
6月
7月
8月
9月
10月
11月
12月
甲地
乙地
(Ⅰ)从上表12个月中,随机取出1个月,求该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率;
(Ⅱ)从上表第一季度和第二季度的6个月中随机取出2个月,记这2个月中甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份的个数为,求的分布列;
(Ⅲ)若,设乙地上表12个月的空气月平均相对湿度的中位数为,求的最大值和最小值.(只需写出结论)
20.(15分)已知函数.
(Ⅰ)当时,求曲线的在点处的切线方程;
(Ⅱ)求函数的单调区间;
(Ⅲ)若恒成立,求的取值范围.
21.(15分)已知函数.
(Ⅰ)求函数的极值;
(Ⅱ)求证:当时,;
(Ⅲ)当时,若曲线在曲线的上方,求实数的取值范围.
2020-2021学年北京市西城区育才学校高二(下)期中数学试卷
参考答案与试题解析
一、选择题:本大题共10小题,每小题4分,共.40分.在每小题给出的四个选项中,只有一项是符合要求的.
1.(4分)在数列中,,且,则等于
A.8
B.6
C.9
D.7
【考点】81:数列的概念及简单表示法
【分析】由条件,得,得到数列是等差数列,然后利用等差数列的性质去判断.
【解答】解:因为,所以,
所以数列是公差的等差数列,首项,
所以,
故选:.
【点评】本题主要考查等差数列的判断以及应用,利用条件转化为等差数列的形式,是解决本题的关键.
2.(4分)函数的导数是
A.
B.
C.
D.
【考点】63:导数的运算
【分析】直接根据函数的导数公式进行求解即可.
【解答】解:,
函数的导数,
故选:.
【点评】本题主要考查函数的导数的计算,根据导数公式是解决本题的关键.比较基础.
3.(4分)将一枚均匀硬币随机掷3次,恰好出现2次正面向上的概率为
A.
B.
C.
D.
【考点】古典概型及其概率计算公式
【分析】将一枚均匀硬币随机投掷3次,利用次独立重复试验中事件恰好发生次的概率计算公式能求出恰好出现2次正面向上的概率.
【解答】解:将一枚均匀硬币随机投掷3次,恰好出现2次正面向上为事件,
则(A).
故选:.
【点评】本题考查概率的求法,注意次独立重复试验中事件恰好发生次的概率计算公式的合理运用.
4.(4分)曲线在点处的切线方程是
A.
B.
C.
D.
【考点】利用导数研究曲线上某点切线方程
【分析】求得的导数,可得切线的斜率,由直线的点斜式方程可得切线的方程.
【解答】解:的导数为,
可得在点处的切线的斜率为,
则在点处的切线的方程为,
即为.
故选:.
【点评】本题考查导数的运用:求切线的方程,考查方程思想和运算能力,属于基础题.
5.(4分)等差数列的首项,公差,如果、、成等比数列,那么等于
A.3
B.
C.2
D.
【考点】83:等差数列的性质;87:等比数列的性质
【分析】利用等差数列的通项公式求出,,利用等比数列的定义列出方程,求出.
【解答】解:等差数列中,有
,
、、成等比数列
解得
故选:.
【点评】本题考查等差数列的通项公式及等比数列的定义.一般列出方程组求出基本量.属于基础题.
6.(4分)函数在
A.内是增函数
B.内是减函数
C.内是增函数,在其余区间内是减函数
D.内是减函数,在其余区间内是增函数
【考点】函数单调性的性质与判断
【分析】对函数进行求导,当导数大于0时原函数单调递增,当导数小于0时原函数单调递减.
【解答】解:函数
当时,解得
故原函数的增区间为:
当时,解得或
故原函数的减区间为:,
故选:.
【点评】本题主要考查通过求函数的导数来确定原函数单调区间的问题.导数大于0时原函数单调递增,当导数小于0时原函数单调递减.
7.(4分)《九章算术》的盈不足章第19个问题中提到:“今有良马与驽马发长安,至齐.齐去长安三千里.良马初日行一百九十三里,日增一十三里.驽马初日行九十七里,日减半里”其大意为:“现在有良马和驽马同时从长安出发到齐去.已知长安和齐的距离是3000里.良马第一天行193里,之后每天比前一天多行13里.驽马第一天行97里,之后每天比前一天少行0.5里”试问前4天,良马和驽马共走过的路程之和的里数为
A.1235
B.1800
C.2600
D.3000
【考点】84:等差数列的通项公式
【分析】利用等差数列前项和公式直接求解.
【解答】解:长安和齐的距离是3000里.良马第一天行193里,之后每天比前一天多行13里.
驽马第一天行97里,之后每天比前一天少行0.5里,
前4天,良马和驽马共走过的路程之和的里数为:
.
故选:.
【点评】本题考查等差数列的前4项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.
8.(4分)函数的大致图象是
A.
B.
C.
D.
【考点】:函数的图象与图象的变换
【分析】判断函数的单调性,计算函数与坐标轴的交点坐标即可得出答案.
【解答】解:,
令得,
当时,,当时,,
在上单调递减,在,上单调递增,
当时,,函数图象与轴交于点;
令得,只有1个零点,
当时,,当时,,
综上,函数图象为.
故选:.
【点评】本题考查了函数的图象判断,函数单调性、零点、极值的计算,属于中档题.
9.(4分)甲、乙、丙、丁4个人进行网球比赛,首先甲、乙一组,丙、丁一组进行比赛,两组的胜者进入决赛,决赛的胜者为冠军、败者为亚军,4个人相互比赛的胜率如表所示,表中的数字表示所在行选手击败其所在列选手的概率.
甲
乙
丙
丁
甲
0.3
0.3
0.8
乙
0.7
0.6
0.4
丙
0.7
0.4
0.5
丁
0.2
0.6
0.5
那么甲得冠军且丙得亚军的概率是
A.0.21
B.0.15
C.0.105
D.0.045
【考点】古典概型及其概率计算公式
【分析】根据表中数据,结合相互独立事件的概率乘法公式处理即可.
【解答】解:甲,乙比赛甲获胜的概率是0.3,
丙,丁比赛丙获胜的概率是0.5,
甲,丙比赛甲获胜的概率是0.3,
根据相互独立事件的概率乘法公式,
甲得冠军丙得亚军的概率为.
故选:.
【点评】本题考查相互独立事件概率,考查数据处理能力,考查化归与转化思想,是基础题.
10.(4分)函数的图象如图所示,且在与处取得极值,给出下列判断:
①;
②(1);
③函数在区间上是增函数.
其中正确的判断是
A.①③
B.②
C.②③
D.①②
【考点】:利用导数研究函数的单调性
【分析】求出函数的导数,根据在与处取得极值,求出,,之间的关系,即可得到结论.
【解答】解:函数,且在与处取得极值,
,且,
则与是方程的两个不同的根,
即,,
则,,
由图象可知,,故①不正确.
(1),且,
(1),故②正确.
是开口向上,对称轴为
函数在区间上是增函数,故③正确
故正确的命题是②③,
故选:.
【点评】本题主要考查导数研究函数的应用,求出函数的导数,结合二次函数的性质,判断,,的大小是解决本题的关键.
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.
11.(5分)设是等差数列的前项和,若,则 10 .
【考点】等差数列的前项和
【分析】由等差数列的前项和公式和通项公式得,由此能求出结果.
【解答】解:是等差数列的前项和,,
.
故答案为:10.
【点评】本题考查等差数列的运算,考查等差数列的性质等基础知识,考查运算求解能力等数学核心素养,是基础题.
12.(5分)已知函数,则(1) .
【考点】导数的运算
【分析】根据对数函数和复合函数的求导公式求出,然后将换上1即可求出(1)的值.
【解答】解:,
,
.
故答案为:.
【点评】本题考查了对数函数和复合函数的求导公式,已知函数求值的方法,考查了计算能力,属于基础题.
13.(5分)离散型随机变量的分布列为:
1
2
3
且,则 ; .
【考点】离散型随机变量及其分布列
【分析】由,利用离散型随机变量的分布列,列出方程组,由此能求出解得,.
【解答】解:,
由离散型随机变量的分布列,得:
,
解得,.
故答案为:,.
【点评】本题考查概率的求法,考查古典概型、离散型随机变量的分布列等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.
14.(5分)等比数列满足如下条件:①;②数列单调递增,试写出满足上述所有条件的一个数列的通项公式 .
【考点】等比数列的通项公式
【分析】利用等比数列的性质直接求解.
【解答】解:等比数列满足如下条件:①;②数列单调递增,
满足上述所有条件的一个数列的通项公式可以是:
.
故答案为:.
【点评】本题考查等比数列的通项公式的求法,考查等比数列的性质等基础知识,考查运算求解能力等数学核心素养,是基础题.
15.(5分)研究函数的性质,完成下面两个问题:
①将(2),(3),(5)按从小到大排列为 (5)(2)(3) ;
②若方程有两个不同的实根,则实数的取值范围是 .
【考点】函数的零点与方程根的关系;利用导数研究函数的单调性
【分析】①利用导数判断在上单调递增,在上单调递减,得出(3)(5),运用作差判断(2)与(5),(2)与(3)的大小,即可得出结论;
②有的单调性可得的最值,将方程有两个不同的实根,转化为函数与的图象有两个交点,从而可求得的取值范围.
【解答】解:①函数,
,
令,可得,
令,可得,
所以在上单调递增,在上单调递减,
(3)(5),
(2)(5)
(2)(5)
(2)(3)
(3)(2),
(5)(2)(3).
②由①可知(e),
在上,,
在上,当时,,
方程有两个不同的实根,
即函数与的图象有两个交点,
故,
即实数的取值范围是
故答案为:(5)(2)(3);.
【点评】本题主要考查利用导数研究函数的单调性,考查函数值大小的比较,方程的根与函数图象交点的关系,考查转化思想与运算求解能力,属于中档题.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(13分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为与,且乙投球2次均未命中的概率为.
(Ⅰ)求甲投球2次,至少命中1次的概率;
(Ⅱ)若甲、乙两人各投球2次,求两人共命中3次的概率.
【考点】:互斥事件的概率加法公式;:相互独立事件和相互独立事件的概率乘法公式
【分析】(Ⅰ)求出甲投球2次都没有命中的概率,再用1减去此概率,即为所求.
(Ⅱ)求出甲只有一次没有命中、乙2次全部命中的概率,再求出乙只有一次没有命中、甲2次全部命中的概率,把这两个概率相加,即为所求.
【解答】解:(Ⅰ)由题意,甲投球2次,都没有命中的概率为,
故甲至少命中1次的概率为.
(Ⅱ)乙投球2次均未命中的概率为,.
若甲、乙两人各投球2次,求两人共命中3次,
则甲只有一次没有命中、乙2次全部命中,或乙只有一次没有命中、甲2次全部命中.
而甲只有一次没有命中、乙2次全部命中的概率为,
而乙只有一次没有命中、甲2次全部命中的概率为,
故两人共命中3次的概率为.
【点评】本题主要考查相互独立事件的概率乘法公式的应用,事件和它的对立事件概率间的关系,属于基础题.
17.(14分)已知函数.
(Ⅰ)求函数的单调增区间和减区间;
(Ⅱ)当,时,求函数的最值和最值点.
【考点】利用导数研究函数的最值;利用导数研究函数的单调性
【分析】分别解出,令,即可得出函数的单调区间.
(Ⅱ)由可得:函数的单调性极值与最值.
【解答】解:函数.
,
令,解得,.
令,解得,或.令,解得.
函数的单调增区间为,;减区间为,.
(Ⅱ)由可得:函数在区间,上单调递增,在,上单调递减,在,上单调递增.
可得:时,函数取得极大值;时,函数取得极小值.
,(1),,(2).
时,函数取得最大值7;时,函数取得最小值.
【点评】本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于中档题.
18.(14分)已知数列中,,______,其中.
(Ⅰ)求数列的通项公式:
(Ⅱ)设,求证:数列是等比数列;
(Ⅲ)求数列的前项和.
从①前项和,②,③且,这三个条件中任选一个,补充在上面的问题中并作答.
【考点】等比数列的性质;数列的求和
【分析】分别选①②③,(Ⅰ)由数列的递推式或等差数列的定义和性质,可得公差,通项公式;(Ⅱ)由等比数列的定义,可得证明;
(Ⅲ)求得,由数列的分组求和,结合等差数列和等比数列的求和公式,可得所求和.
【解答】解:选①,(Ⅰ)因为,时,,
则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
.
选②,(Ⅰ)由,,则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
.
选③,(Ⅰ)由,且,
可得数列为等差数列,设公差为,
则,
则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
所以
.
【点评】本题考查等差数列的定义和通项公式、等比数列的定义与求和公式,考查方程思想和运算能力,属于中档题.
19.(14分)流行性感冒多由病毒引起,据调查,空气月平均相对湿度过大或过小时,都有利于一些病毒繁殖和传播,科学测定,当空气月平均相对湿度大于或小于时,有利于病毒繁殖和传播.下表记录了某年甲、乙两个城市12个月的空气月平均相对湿度
第一季度
第二季度
第三季度
第四季度
1月
2月
3月
4月
5月
6月
7月
8月
9月
10月
11月
12月
甲地
乙地
(Ⅰ)从上表12个月中,随机取出1个月,求该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率;
(Ⅱ)从上表第一季度和第二季度的6个月中随机取出2个月,记这2个月中甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份的个数为,求的分布列;
(Ⅲ)若,设乙地上表12个月的空气月平均相对湿度的中位数为,求的最大值和最小值.(只需写出结论)
【考点】离散型随机变量及其分布列
【分析】(Ⅰ)设事件:从上表12个月中,随机取出1个月,该月甲地空气月平均相对湿度有利于病毒繁殖和传播.用表示事件抽取的月份为第月,利用列举法能求出该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率.
(Ⅱ)在第一季度和第二季度的6个月中,甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份只有2月和6月,所有可能的取值为0,1,2.分别求出相应的概率,由此能求出随机变量的分布列.
(Ⅲ),设乙地上表12个月的空气月平均相对湿度的中位数为,由此能求出的最大值,最小值.
【解答】(本题满分13分)
解:(Ⅰ)设事件:从上表12个月中,随机取出1个月,
该月甲地空气月平均相对湿度有利于病毒繁殖和传播.
用表示事件抽取的月份为第月,
则,,,,,,,,,,,共12个基本事件,
,,,,,共6个基本事件,
所以,该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率.(4分)
(Ⅱ)在第一季度和第二季度的6个月中,
甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份只有2月和6月,
故所有可能的取值为0,1,2.
,
,
随机变量的分布列为:
0
1
2
(Ⅲ),设乙地上表12个月的空气月平均相对湿度的中位数为,
则的最大值为,最小值为.(13分)
【点评】本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法及应用,考查中位数的求法,考查运算求解能力,考查函数与方程思想,是中档题.
20.(15分)已知函数.
(Ⅰ)当时,求曲线的在点处的切线方程;
(Ⅱ)求函数的单调区间;
(Ⅲ)若恒成立,求的取值范围.
【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的最值;利用导数研究函数的单调性
【分析】函数.当时,,(1).切线的斜率为(1),利用点斜式即可得出曲线的在点处的切线方程.
(Ⅱ),.对分类讨论即可得出单调区间.
(Ⅲ)若恒成立,则在上恒成立.令,.利用导数研究其单调性即可得出函数取得极值与最值.
【解答】解:函数.
当时,,(1).
,
(1),
曲线的在点处的切线方程为:,即.
(Ⅱ),.
时,,函数在上单调递减.
时,,
则函数在上单调递减,在,上单调递增.
(Ⅲ)若恒成立,则在上恒成立.
令,.
,
可得时,函数取得极大值即最大值.
(e).
的取值范围为,.
【点评】本题考查了利用导数研究函数的单调性极值与最值、切线方程,考查了推理能力与计算能力,属于中档题.
21.(15分)已知函数.
(Ⅰ)求函数的极值;
(Ⅱ)求证:当时,;
(Ⅲ)当时,若曲线在曲线的上方,求实数的取值范围.
【考点】:利用导数研究函数的极值;:利用导数研究函数的单调性
【分析】(Ⅰ)求导,列出随的变化,和的情况表,进而求得极值;
(Ⅱ)令,求导,由得,则,进而得出函数的单调性,由此得证;
(Ⅲ)当时,由(Ⅱ)知符合题意,再令,分及均可判断不合题意,进而得出实数的取值范围.
【解答】解:(Ⅰ)因为,定义域,
所以.
令,解得.
随的变化,和的情况如下:
0
0
增
极大值
减
由表可知函数在时取得极大值,无极小值;
(Ⅱ)证明:令,.
由得,
于是,
故函数是,上的增函数.
所以当时,,即;
(Ⅲ)当时,由(Ⅱ)知,满足题意.
令,.
当时,若,,则在上是减函数.
所以时,,不合题意.
当时,,则在上是减函数,所以,不合题意.
综上所述,实数的取值范围.
【点评】本题考查利用导数研究函数的单调性,极值及最值,考查分类讨论思想及运算求解能力,属于中档题.
一、选择题:本大题共10小题,每小题4分,共.40分.在每小题给出的四个选项中,只有一项是符合要求的.
1.(4分)在数列中,,且,则等于
A.8
B.6
C.9
D.7
2.(4分)函数的导数是
A.
B.
C.
D.
3.(4分)将一枚均匀硬币随机掷3次,恰好出现2次正面向上的概率为
A.
B.
C.
D.
4.(4分)曲线在点处的切线方程是
A.
B.
C.
D.
5.(4分)等差数列的首项,公差,如果、、成等比数列,那么等于
A.3
B.
C.2
D.
6.(4分)函数在
A.内是增函数
B.内是减函数
C.内是增函数,在其余区间内是减函数
D.内是减函数,在其余区间内是增函数
7.(4分)《九章算术》的盈不足章第19个问题中提到:“今有良马与驽马发长安,至齐.齐去长安三千里.良马初日行一百九十三里,日增一十三里.驽马初日行九十七里,日减半里”其大意为:“现在有良马和驽马同时从长安出发到齐去.已知长安和齐的距离是3000里.良马第一天行193里,之后每天比前一天多行13里.驽马第一天行97里,之后每天比前一天少行0.5里”试问前4天,良马和驽马共走过的路程之和的里数为
A.1235
B.1800
C.2600
D.3000
8.(4分)函数的大致图象是
A.
B.
C.
D.
9.(4分)甲、乙、丙、丁4个人进行网球比赛,首先甲、乙一组,丙、丁一组进行比赛,两组的胜者进入决赛,决赛的胜者为冠军、败者为亚军,4个人相互比赛的胜率如表所示,表中的数字表示所在行选手击败其所在列选手的概率.
甲
乙
丙
丁
甲
0.3
0.3
0.8
乙
0.7
0.6
0.4
丙
0.7
0.4
0.5
丁
0.2
0.6
0.5
那么甲得冠军且丙得亚军的概率是
A.0.21
B.0.15
C.0.105
D.0.045
10.(4分)函数的图象如图所示,且在与处取得极值,给出下列判断:
①;
②(1);
③函数在区间上是增函数.
其中正确的判断是
A.①③
B.②
C.②③
D.①②
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.
11.(5分)设是等差数列的前项和,若,则 .
12.(5分)已知函数,则(1) .
13.(5分)离散型随机变量的分布列为:
1
2
3
且,则 ; .
14.(5分)等比数列满足如下条件:①;②数列单调递增,试写出满足上述所有条件的一个数列的通项公式 .
15.(5分)研究函数的性质,完成下面两个问题:
①将(2),(3),(5)按从小到大排列为 ;
②若方程有两个不同的实根,则实数的取值范围是 .
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(13分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为与,且乙投球2次均未命中的概率为.
(Ⅰ)求甲投球2次,至少命中1次的概率;
(Ⅱ)若甲、乙两人各投球2次,求两人共命中3次的概率.
17.(14分)已知函数.
(Ⅰ)求函数的单调增区间和减区间;
(Ⅱ)当,时,求函数的最值和最值点.
18.(14分)已知数列中,,______,其中.
(Ⅰ)求数列的通项公式:
(Ⅱ)设,求证:数列是等比数列;
(Ⅲ)求数列的前项和.
从①前项和,②,③且,这三个条件中任选一个,补充在上面的问题中并作答.
19.(14分)流行性感冒多由病毒引起,据调查,空气月平均相对湿度过大或过小时,都有利于一些病毒繁殖和传播,科学测定,当空气月平均相对湿度大于或小于时,有利于病毒繁殖和传播.下表记录了某年甲、乙两个城市12个月的空气月平均相对湿度
第一季度
第二季度
第三季度
第四季度
1月
2月
3月
4月
5月
6月
7月
8月
9月
10月
11月
12月
甲地
乙地
(Ⅰ)从上表12个月中,随机取出1个月,求该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率;
(Ⅱ)从上表第一季度和第二季度的6个月中随机取出2个月,记这2个月中甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份的个数为,求的分布列;
(Ⅲ)若,设乙地上表12个月的空气月平均相对湿度的中位数为,求的最大值和最小值.(只需写出结论)
20.(15分)已知函数.
(Ⅰ)当时,求曲线的在点处的切线方程;
(Ⅱ)求函数的单调区间;
(Ⅲ)若恒成立,求的取值范围.
21.(15分)已知函数.
(Ⅰ)求函数的极值;
(Ⅱ)求证:当时,;
(Ⅲ)当时,若曲线在曲线的上方,求实数的取值范围.
2020-2021学年北京市西城区育才学校高二(下)期中数学试卷
参考答案与试题解析
一、选择题:本大题共10小题,每小题4分,共.40分.在每小题给出的四个选项中,只有一项是符合要求的.
1.(4分)在数列中,,且,则等于
A.8
B.6
C.9
D.7
【考点】81:数列的概念及简单表示法
【分析】由条件,得,得到数列是等差数列,然后利用等差数列的性质去判断.
【解答】解:因为,所以,
所以数列是公差的等差数列,首项,
所以,
故选:.
【点评】本题主要考查等差数列的判断以及应用,利用条件转化为等差数列的形式,是解决本题的关键.
2.(4分)函数的导数是
A.
B.
C.
D.
【考点】63:导数的运算
【分析】直接根据函数的导数公式进行求解即可.
【解答】解:,
函数的导数,
故选:.
【点评】本题主要考查函数的导数的计算,根据导数公式是解决本题的关键.比较基础.
3.(4分)将一枚均匀硬币随机掷3次,恰好出现2次正面向上的概率为
A.
B.
C.
D.
【考点】古典概型及其概率计算公式
【分析】将一枚均匀硬币随机投掷3次,利用次独立重复试验中事件恰好发生次的概率计算公式能求出恰好出现2次正面向上的概率.
【解答】解:将一枚均匀硬币随机投掷3次,恰好出现2次正面向上为事件,
则(A).
故选:.
【点评】本题考查概率的求法,注意次独立重复试验中事件恰好发生次的概率计算公式的合理运用.
4.(4分)曲线在点处的切线方程是
A.
B.
C.
D.
【考点】利用导数研究曲线上某点切线方程
【分析】求得的导数,可得切线的斜率,由直线的点斜式方程可得切线的方程.
【解答】解:的导数为,
可得在点处的切线的斜率为,
则在点处的切线的方程为,
即为.
故选:.
【点评】本题考查导数的运用:求切线的方程,考查方程思想和运算能力,属于基础题.
5.(4分)等差数列的首项,公差,如果、、成等比数列,那么等于
A.3
B.
C.2
D.
【考点】83:等差数列的性质;87:等比数列的性质
【分析】利用等差数列的通项公式求出,,利用等比数列的定义列出方程,求出.
【解答】解:等差数列中,有
,
、、成等比数列
解得
故选:.
【点评】本题考查等差数列的通项公式及等比数列的定义.一般列出方程组求出基本量.属于基础题.
6.(4分)函数在
A.内是增函数
B.内是减函数
C.内是增函数,在其余区间内是减函数
D.内是减函数,在其余区间内是增函数
【考点】函数单调性的性质与判断
【分析】对函数进行求导,当导数大于0时原函数单调递增,当导数小于0时原函数单调递减.
【解答】解:函数
当时,解得
故原函数的增区间为:
当时,解得或
故原函数的减区间为:,
故选:.
【点评】本题主要考查通过求函数的导数来确定原函数单调区间的问题.导数大于0时原函数单调递增,当导数小于0时原函数单调递减.
7.(4分)《九章算术》的盈不足章第19个问题中提到:“今有良马与驽马发长安,至齐.齐去长安三千里.良马初日行一百九十三里,日增一十三里.驽马初日行九十七里,日减半里”其大意为:“现在有良马和驽马同时从长安出发到齐去.已知长安和齐的距离是3000里.良马第一天行193里,之后每天比前一天多行13里.驽马第一天行97里,之后每天比前一天少行0.5里”试问前4天,良马和驽马共走过的路程之和的里数为
A.1235
B.1800
C.2600
D.3000
【考点】84:等差数列的通项公式
【分析】利用等差数列前项和公式直接求解.
【解答】解:长安和齐的距离是3000里.良马第一天行193里,之后每天比前一天多行13里.
驽马第一天行97里,之后每天比前一天少行0.5里,
前4天,良马和驽马共走过的路程之和的里数为:
.
故选:.
【点评】本题考查等差数列的前4项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.
8.(4分)函数的大致图象是
A.
B.
C.
D.
【考点】:函数的图象与图象的变换
【分析】判断函数的单调性,计算函数与坐标轴的交点坐标即可得出答案.
【解答】解:,
令得,
当时,,当时,,
在上单调递减,在,上单调递增,
当时,,函数图象与轴交于点;
令得,只有1个零点,
当时,,当时,,
综上,函数图象为.
故选:.
【点评】本题考查了函数的图象判断,函数单调性、零点、极值的计算,属于中档题.
9.(4分)甲、乙、丙、丁4个人进行网球比赛,首先甲、乙一组,丙、丁一组进行比赛,两组的胜者进入决赛,决赛的胜者为冠军、败者为亚军,4个人相互比赛的胜率如表所示,表中的数字表示所在行选手击败其所在列选手的概率.
甲
乙
丙
丁
甲
0.3
0.3
0.8
乙
0.7
0.6
0.4
丙
0.7
0.4
0.5
丁
0.2
0.6
0.5
那么甲得冠军且丙得亚军的概率是
A.0.21
B.0.15
C.0.105
D.0.045
【考点】古典概型及其概率计算公式
【分析】根据表中数据,结合相互独立事件的概率乘法公式处理即可.
【解答】解:甲,乙比赛甲获胜的概率是0.3,
丙,丁比赛丙获胜的概率是0.5,
甲,丙比赛甲获胜的概率是0.3,
根据相互独立事件的概率乘法公式,
甲得冠军丙得亚军的概率为.
故选:.
【点评】本题考查相互独立事件概率,考查数据处理能力,考查化归与转化思想,是基础题.
10.(4分)函数的图象如图所示,且在与处取得极值,给出下列判断:
①;
②(1);
③函数在区间上是增函数.
其中正确的判断是
A.①③
B.②
C.②③
D.①②
【考点】:利用导数研究函数的单调性
【分析】求出函数的导数,根据在与处取得极值,求出,,之间的关系,即可得到结论.
【解答】解:函数,且在与处取得极值,
,且,
则与是方程的两个不同的根,
即,,
则,,
由图象可知,,故①不正确.
(1),且,
(1),故②正确.
是开口向上,对称轴为
函数在区间上是增函数,故③正确
故正确的命题是②③,
故选:.
【点评】本题主要考查导数研究函数的应用,求出函数的导数,结合二次函数的性质,判断,,的大小是解决本题的关键.
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.
11.(5分)设是等差数列的前项和,若,则 10 .
【考点】等差数列的前项和
【分析】由等差数列的前项和公式和通项公式得,由此能求出结果.
【解答】解:是等差数列的前项和,,
.
故答案为:10.
【点评】本题考查等差数列的运算,考查等差数列的性质等基础知识,考查运算求解能力等数学核心素养,是基础题.
12.(5分)已知函数,则(1) .
【考点】导数的运算
【分析】根据对数函数和复合函数的求导公式求出,然后将换上1即可求出(1)的值.
【解答】解:,
,
.
故答案为:.
【点评】本题考查了对数函数和复合函数的求导公式,已知函数求值的方法,考查了计算能力,属于基础题.
13.(5分)离散型随机变量的分布列为:
1
2
3
且,则 ; .
【考点】离散型随机变量及其分布列
【分析】由,利用离散型随机变量的分布列,列出方程组,由此能求出解得,.
【解答】解:,
由离散型随机变量的分布列,得:
,
解得,.
故答案为:,.
【点评】本题考查概率的求法,考查古典概型、离散型随机变量的分布列等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.
14.(5分)等比数列满足如下条件:①;②数列单调递增,试写出满足上述所有条件的一个数列的通项公式 .
【考点】等比数列的通项公式
【分析】利用等比数列的性质直接求解.
【解答】解:等比数列满足如下条件:①;②数列单调递增,
满足上述所有条件的一个数列的通项公式可以是:
.
故答案为:.
【点评】本题考查等比数列的通项公式的求法,考查等比数列的性质等基础知识,考查运算求解能力等数学核心素养,是基础题.
15.(5分)研究函数的性质,完成下面两个问题:
①将(2),(3),(5)按从小到大排列为 (5)(2)(3) ;
②若方程有两个不同的实根,则实数的取值范围是 .
【考点】函数的零点与方程根的关系;利用导数研究函数的单调性
【分析】①利用导数判断在上单调递增,在上单调递减,得出(3)(5),运用作差判断(2)与(5),(2)与(3)的大小,即可得出结论;
②有的单调性可得的最值,将方程有两个不同的实根,转化为函数与的图象有两个交点,从而可求得的取值范围.
【解答】解:①函数,
,
令,可得,
令,可得,
所以在上单调递增,在上单调递减,
(3)(5),
(2)(5)
(2)(5)
(2)(3)
(3)(2),
(5)(2)(3).
②由①可知(e),
在上,,
在上,当时,,
方程有两个不同的实根,
即函数与的图象有两个交点,
故,
即实数的取值范围是
故答案为:(5)(2)(3);.
【点评】本题主要考查利用导数研究函数的单调性,考查函数值大小的比较,方程的根与函数图象交点的关系,考查转化思想与运算求解能力,属于中档题.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(13分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为与,且乙投球2次均未命中的概率为.
(Ⅰ)求甲投球2次,至少命中1次的概率;
(Ⅱ)若甲、乙两人各投球2次,求两人共命中3次的概率.
【考点】:互斥事件的概率加法公式;:相互独立事件和相互独立事件的概率乘法公式
【分析】(Ⅰ)求出甲投球2次都没有命中的概率,再用1减去此概率,即为所求.
(Ⅱ)求出甲只有一次没有命中、乙2次全部命中的概率,再求出乙只有一次没有命中、甲2次全部命中的概率,把这两个概率相加,即为所求.
【解答】解:(Ⅰ)由题意,甲投球2次,都没有命中的概率为,
故甲至少命中1次的概率为.
(Ⅱ)乙投球2次均未命中的概率为,.
若甲、乙两人各投球2次,求两人共命中3次,
则甲只有一次没有命中、乙2次全部命中,或乙只有一次没有命中、甲2次全部命中.
而甲只有一次没有命中、乙2次全部命中的概率为,
而乙只有一次没有命中、甲2次全部命中的概率为,
故两人共命中3次的概率为.
【点评】本题主要考查相互独立事件的概率乘法公式的应用,事件和它的对立事件概率间的关系,属于基础题.
17.(14分)已知函数.
(Ⅰ)求函数的单调增区间和减区间;
(Ⅱ)当,时,求函数的最值和最值点.
【考点】利用导数研究函数的最值;利用导数研究函数的单调性
【分析】分别解出,令,即可得出函数的单调区间.
(Ⅱ)由可得:函数的单调性极值与最值.
【解答】解:函数.
,
令,解得,.
令,解得,或.令,解得.
函数的单调增区间为,;减区间为,.
(Ⅱ)由可得:函数在区间,上单调递增,在,上单调递减,在,上单调递增.
可得:时,函数取得极大值;时,函数取得极小值.
,(1),,(2).
时,函数取得最大值7;时,函数取得最小值.
【点评】本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于中档题.
18.(14分)已知数列中,,______,其中.
(Ⅰ)求数列的通项公式:
(Ⅱ)设,求证:数列是等比数列;
(Ⅲ)求数列的前项和.
从①前项和,②,③且,这三个条件中任选一个,补充在上面的问题中并作答.
【考点】等比数列的性质;数列的求和
【分析】分别选①②③,(Ⅰ)由数列的递推式或等差数列的定义和性质,可得公差,通项公式;(Ⅱ)由等比数列的定义,可得证明;
(Ⅲ)求得,由数列的分组求和,结合等差数列和等比数列的求和公式,可得所求和.
【解答】解:选①,(Ⅰ)因为,时,,
则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
.
选②,(Ⅰ)由,,则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
.
选③,(Ⅰ)由,且,
可得数列为等差数列,设公差为,
则,
则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
所以
.
【点评】本题考查等差数列的定义和通项公式、等比数列的定义与求和公式,考查方程思想和运算能力,属于中档题.
19.(14分)流行性感冒多由病毒引起,据调查,空气月平均相对湿度过大或过小时,都有利于一些病毒繁殖和传播,科学测定,当空气月平均相对湿度大于或小于时,有利于病毒繁殖和传播.下表记录了某年甲、乙两个城市12个月的空气月平均相对湿度
第一季度
第二季度
第三季度
第四季度
1月
2月
3月
4月
5月
6月
7月
8月
9月
10月
11月
12月
甲地
乙地
(Ⅰ)从上表12个月中,随机取出1个月,求该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率;
(Ⅱ)从上表第一季度和第二季度的6个月中随机取出2个月,记这2个月中甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份的个数为,求的分布列;
(Ⅲ)若,设乙地上表12个月的空气月平均相对湿度的中位数为,求的最大值和最小值.(只需写出结论)
【考点】离散型随机变量及其分布列
【分析】(Ⅰ)设事件:从上表12个月中,随机取出1个月,该月甲地空气月平均相对湿度有利于病毒繁殖和传播.用表示事件抽取的月份为第月,利用列举法能求出该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率.
(Ⅱ)在第一季度和第二季度的6个月中,甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份只有2月和6月,所有可能的取值为0,1,2.分别求出相应的概率,由此能求出随机变量的分布列.
(Ⅲ),设乙地上表12个月的空气月平均相对湿度的中位数为,由此能求出的最大值,最小值.
【解答】(本题满分13分)
解:(Ⅰ)设事件:从上表12个月中,随机取出1个月,
该月甲地空气月平均相对湿度有利于病毒繁殖和传播.
用表示事件抽取的月份为第月,
则,,,,,,,,,,,共12个基本事件,
,,,,,共6个基本事件,
所以,该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率.(4分)
(Ⅱ)在第一季度和第二季度的6个月中,
甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份只有2月和6月,
故所有可能的取值为0,1,2.
,
,
随机变量的分布列为:
0
1
2
(Ⅲ),设乙地上表12个月的空气月平均相对湿度的中位数为,
则的最大值为,最小值为.(13分)
【点评】本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法及应用,考查中位数的求法,考查运算求解能力,考查函数与方程思想,是中档题.
20.(15分)已知函数.
(Ⅰ)当时,求曲线的在点处的切线方程;
(Ⅱ)求函数的单调区间;
(Ⅲ)若恒成立,求的取值范围.
【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的最值;利用导数研究函数的单调性
【分析】函数.当时,,(1).切线的斜率为(1),利用点斜式即可得出曲线的在点处的切线方程.
(Ⅱ),.对分类讨论即可得出单调区间.
(Ⅲ)若恒成立,则在上恒成立.令,.利用导数研究其单调性即可得出函数取得极值与最值.
【解答】解:函数.
当时,,(1).
,
(1),
曲线的在点处的切线方程为:,即.
(Ⅱ),.
时,,函数在上单调递减.
时,,
则函数在上单调递减,在,上单调递增.
(Ⅲ)若恒成立,则在上恒成立.
令,.
,
可得时,函数取得极大值即最大值.
(e).
的取值范围为,.
【点评】本题考查了利用导数研究函数的单调性极值与最值、切线方程,考查了推理能力与计算能力,属于中档题.
21.(15分)已知函数.
(Ⅰ)求函数的极值;
(Ⅱ)求证:当时,;
(Ⅲ)当时,若曲线在曲线的上方,求实数的取值范围.
【考点】:利用导数研究函数的极值;:利用导数研究函数的单调性
【分析】(Ⅰ)求导,列出随的变化,和的情况表,进而求得极值;
(Ⅱ)令,求导,由得,则,进而得出函数的单调性,由此得证;
(Ⅲ)当时,由(Ⅱ)知符合题意,再令,分及均可判断不合题意,进而得出实数的取值范围.
【解答】解:(Ⅰ)因为,定义域,
所以.
令,解得.
随的变化,和的情况如下:
0
0
增
极大值
减
由表可知函数在时取得极大值,无极小值;
(Ⅱ)证明:令,.
由得,
于是,
故函数是,上的增函数.
所以当时,,即;
(Ⅲ)当时,由(Ⅱ)知,满足题意.
令,.
当时,若,,则在上是减函数.
所以时,,不合题意.
当时,,则在上是减函数,所以,不合题意.
综上所述,实数的取值范围.
【点评】本题考查利用导数研究函数的单调性,极值及最值,考查分类讨论思想及运算求解能力,属于中档题.
同课章节目录
