2021-2022学年湘教新版九年级上册数学《第3章 图形的相似》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湘教新版九年级上册数学《第3章 图形的相似》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 378.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览



文档简介
2021-2022学年湘教新版九年级上册数学《第3章
图形的相似》单元测试卷
一.选择题
1.若,则的值为( )
A.
B.
C.
D.
2.在一幅比例尺为1:500000的地图上,若量得甲、乙两地的距离是25cm,则甲、乙两地实际距离为( )
A.125km
B.12.5km
C.1.25km
D.1250km
3.已知P是线段AB的黄金分割点,且PA>PB、如果S1表示以PA为一边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,则S1与S2之间的大小关系是( )
A.S1=S2
B.S1>S2
C.S1<S2
D.S1与S2的大小关系不能确定
4.如图,E是平行四边形ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
A.
B.
C.
D.
5.下列图形一定相似的是( )
A.两个矩形
B.两个等腰梯形
C.有一个内角相等的两个菱形
D.对应边成比例的两个四边形
6.将直角三角形三边扩大同样的倍数,得到的新的三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.任意三角形
7.已知,则的值为( )
A.
B.
C.
D.
8.如图,在△ABC中,DE∥BC,,DE=4cm,则BC的长为( )
A.8cm
B.12cm
C.11cm
D.10cm
9.如图,已知:△ABC∽△DAC,∠B=36°,∠D=117°,∠BAD的度数为( )
A.36°
B.117°
C.143°
D.153°
10.已知a、b、c均不为0,且a+b+c≠0,若===k,则k=( )
A.﹣1
B.0
C.2
D.3
二.填空题
11.已知x:y:z=1:2:3,且x﹣2y+3z=4,则x﹣y+z=
.
12.若2a=3b,则a:b=
.
13.在比例尺为1:500000的地图上,测得A、B两地间的图上距离为6cm,则A、B两地间实际距离
km.
14.如图,用放大镜将图形放大,应属于哪一种变换:
(请选填:对称变换、平移变换、旋转变换、相似变换).
15.请指出图中从图1到图2的变换是
变换.
16.如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=
.
17.如果=,那么=
.
18.已知点P是线段AB的黄金分割点,且AP>BP,AB=4,那么AP=
.
19.直线CD∥EF,若OC=3,CE=4,则的值是
.
20.如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB边的中点,P是BC边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与△ABC相似,则线段PC=
.
三.解答题
21.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
22.已知:线段a、b、c,且==.
(1)求的值.
(2)如线段a、b、c满足a+b+c=27.求a、b、c的值.
23.已知,求的值.
24.如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,AB=7,BD=2,AE=6,求AC的长.
25.已知:(x、y、z均不为零),求的值.
26.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
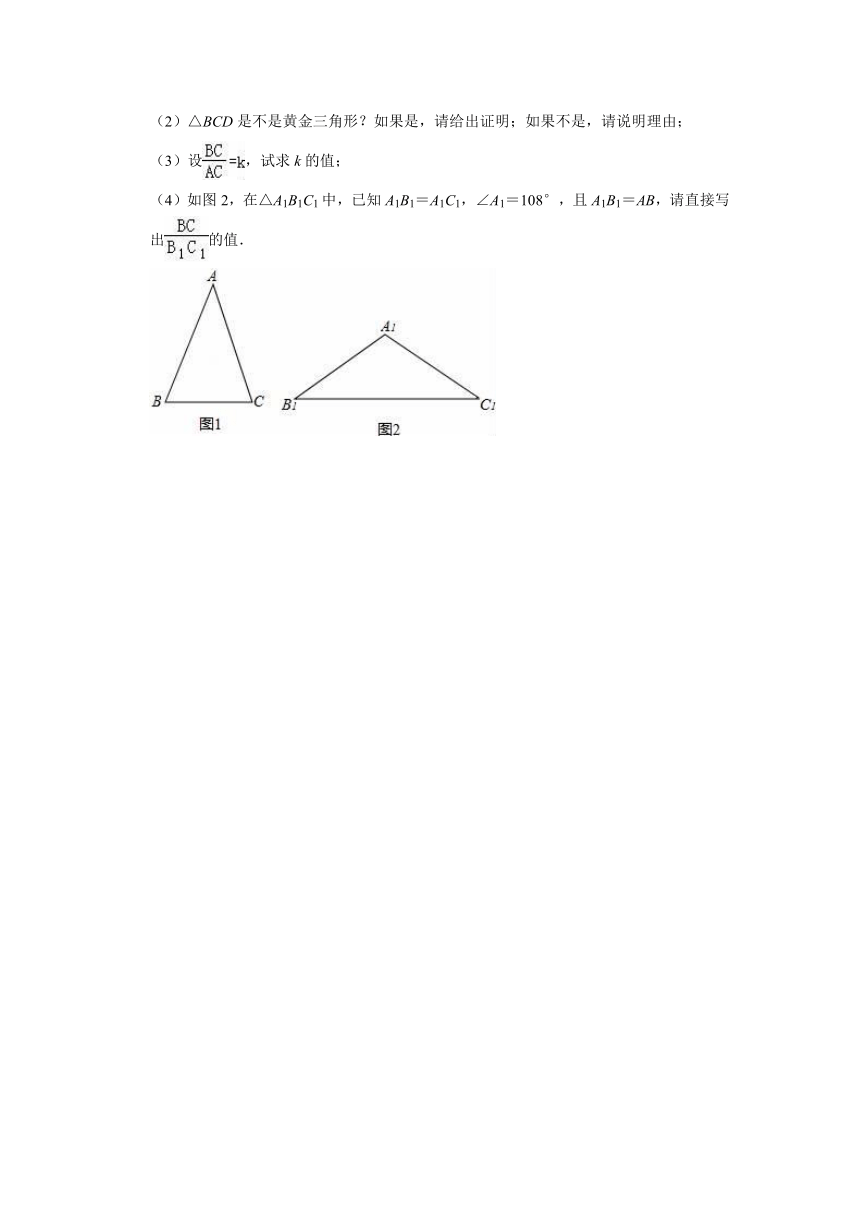
27.三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.
(1)在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);
(2)△BCD是不是黄金三角形?如果是,请给出证明;如果不是,请说明理由;
(3)设,试求k的值;
(4)如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,请直接写出的值.
参考答案与试题解析
一.选择题
1.解:∵=,
∴设x=3k,y=2k(k≠0),
∴==.
故选:A.
2.解:设实际距离为xcm,则:
1:500000=25:x,
解得x=12500000.
12500000cm=125km.
故选:A.
3.解:由题意得:
∴=1.
即:S1=S2.
故选:A.
4.解:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD;AD∥BC,
∴==,而AB=CD,
∴==,而AB=CD,
∴==;
又∵AF∥BC,
∴=.
故选:A.
5.解:A、两个矩形,对应角相等,都是直角,但四条边不一定对应成比例,故本选项不符合题意;
B、两个等腰梯形,四个角不一定对应相等,边也不一定对应成比例,所以不一定相似,故本选项不符合题意;
C、两个菱形,有一个角相等,则其它角也对应相等,而四条边都相等,所以对应成比例,所以相似,故本选项符合题意;
D、对应边成比例,对应角不一定相等,所以不一定相似,故本选项不符合题意.
故选:C.
6.解:因为角的度数和它的两边的长短无关,所以得到的新三角形应该是直角三角形,故选B.
7.解:,则==,
故选:D.
8.解:∵在△ABC中,DE∥BC,
∴△ADE∽△ABC,
∴,
∵,
∴=,
即=,
∵DE=4cm,
∴BC=12cm.
故选:B.
9.解:∵△ABC∽△DAC,
∴∠DAC=∠B=36°,∠BAC=∠D=117°,
∴∠BAD=∠DAC+∠BAC=153°,
故选:D.
10.解:由若===k,得
2b+c=ak,2c+a=bk,2a+b=ck,
三式相加,得3(a+b+c)=k(a+b+c)
由于a、b、c均不为0,且a+b+c≠0,
所以k==3.
故选:D.
二.填空题
11.解:∵x:y:z=1:2:3,
∴设x=t,y=2t,z=3t,
∵x﹣2y+3z=4,
∴t﹣4t+9t=4,
解得t=,
∴x﹣y+z=t﹣2t+3t=2t=2×=.
故答案为.
12.解:∵2a=3b,
∴a:b=3:2.
故答案为:3:2.
13.解:设A、B两地间的实际距离为xcm,由题意,得
1:500000=6:x,
解得x=3000000cm=30km.
故答案为30.
14.解:由一个图形到另一个图形,在改变的过程中形状不变,大小产生变化,属于相似变化.
15.解:∵从图1到图2,图形形状没变,只是大小发生改变,
∴从图1到图2的变换是相似变换.
故答案为:相似,
16.解:作DF∥AE交BC于F,如图,
∵OE∥DF,
∴==1,
即BE=EF,
∵DF∥AE,
∴==,
∴CF=2EF,
∴BE:EC=BE:3BE=1:3.
故答案为1:3.
17.解:∵=,
∴=,
设a=2t,b=3t,
∴==.
故答案为.
18.解:由于P为线段AB=4的黄金分割点,
且AP是较长线段;
则AP=AB=×4=2﹣2.
故答案为2﹣2.
19.解:∵CD∥EF
∴OD:OF=OC:OE
∵OC=3,CE=4
∴OD:OF=OC:OE=3:7.
20.解:∵Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB=10,
∵D是AB边的中点,
∴CD=BD=AB=5,
∵以D、C、P为顶点的三角形与△ABC相似,
∴∠DPC=90°或∠CDP=90°,
(1)若∠DPC=90°,则DP∥AC,
∴=,
∴BP=BC=4,
则PC=4;
(2)若∠CDP=90°,则△CDP∽△BCA,
∴,
即,
∴PC=.
∴PC=4或.
三.解答题
21.解:(1)∵FE∥CD,
∴=,即=,
解得,AC=,
则CE=AC﹣AE=﹣4=;
(2)∵DE∥BC,
∴=,即=,
解得,AB=.
22.解:(1)∵=,
∴=,
∴=,
(2)设===k,
则a=2k,b=3k,c=4k,
∵a+b+c=27,
∴2k+3k+4k=27,
∴k=3,
∴a=6,b=9,c=12.
23.解:设===k≠0,
则x=2k,y=3k,z=4k,
所以,===﹣3.
24.解:∵AB=7,BD=2,
∴AD=AB﹣BD=5.
∵DE∥BC,
∴=.
∵AE=6,
∴=,
∴AC=.
25.解:设=k,则x=6k,y=4k,z=3k
∴===3.
26.解:(1)路线图(6分)(P、A、C点各2分)
注意:起点是必须在所给的图形中画,否则即使画图正确扣;(2分)
(2)量得∠PAC≈105°,∠ACP≈45°;(9分)(只有1个正确得2分)
(3)量路线图得AC≈3.5厘米,PC≈6.8厘米.
∴AC≈3.5千米;PC≈6.8千米(13分)
27.解:(1)如图所示;
(2)△BCD是黄金三角形.
证明如下:∵点D在AB的垂直平分线上,
∴AD=BD,
∴∠ABD=∠A.
∵∠A=36°,AB=AC,
∴∠ABC=∠C=72°,
∴∠ABD=∠DBC=36°.
又∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴△BCD是黄金三角形.
(3)设BC=x,AC=y,
由(2)知,AD=BD=BC=x.
∵∠DBC=∠A,∠C=∠C,
∴△BDC∽△ABC,
∴,即,
整理,得x2+xy﹣y2=0,
解得.
因为x、y均为正数,所以.
(4).
理由:延长BC到E,使CE=AC,连接AE.
∵∠A=36°,AB=AC,
∴∠ACB=∠B=72°,
∴∠ACE=180°﹣72°=108°,
∴∠ACE=∠B1A1C1.
∵A1B1=AB,
∴AC=CE=A1B1=A1C1,
∴△ACE≌△B1A1C1,
∴AE=B1C1.
由(3)知,
∴,,
∴.
图形的相似》单元测试卷
一.选择题
1.若,则的值为( )
A.
B.
C.
D.
2.在一幅比例尺为1:500000的地图上,若量得甲、乙两地的距离是25cm,则甲、乙两地实际距离为( )
A.125km
B.12.5km
C.1.25km
D.1250km
3.已知P是线段AB的黄金分割点,且PA>PB、如果S1表示以PA为一边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,则S1与S2之间的大小关系是( )
A.S1=S2
B.S1>S2
C.S1<S2
D.S1与S2的大小关系不能确定
4.如图,E是平行四边形ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
A.
B.
C.
D.
5.下列图形一定相似的是( )
A.两个矩形
B.两个等腰梯形
C.有一个内角相等的两个菱形
D.对应边成比例的两个四边形
6.将直角三角形三边扩大同样的倍数,得到的新的三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.任意三角形
7.已知,则的值为( )
A.
B.
C.
D.
8.如图,在△ABC中,DE∥BC,,DE=4cm,则BC的长为( )
A.8cm
B.12cm
C.11cm
D.10cm
9.如图,已知:△ABC∽△DAC,∠B=36°,∠D=117°,∠BAD的度数为( )
A.36°
B.117°
C.143°
D.153°
10.已知a、b、c均不为0,且a+b+c≠0,若===k,则k=( )
A.﹣1
B.0
C.2
D.3
二.填空题
11.已知x:y:z=1:2:3,且x﹣2y+3z=4,则x﹣y+z=
.
12.若2a=3b,则a:b=
.
13.在比例尺为1:500000的地图上,测得A、B两地间的图上距离为6cm,则A、B两地间实际距离
km.
14.如图,用放大镜将图形放大,应属于哪一种变换:
(请选填:对称变换、平移变换、旋转变换、相似变换).
15.请指出图中从图1到图2的变换是
变换.
16.如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=
.
17.如果=,那么=
.
18.已知点P是线段AB的黄金分割点,且AP>BP,AB=4,那么AP=
.
19.直线CD∥EF,若OC=3,CE=4,则的值是
.
20.如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB边的中点,P是BC边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与△ABC相似,则线段PC=
.
三.解答题
21.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
22.已知:线段a、b、c,且==.
(1)求的值.
(2)如线段a、b、c满足a+b+c=27.求a、b、c的值.
23.已知,求的值.
24.如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,AB=7,BD=2,AE=6,求AC的长.
25.已知:(x、y、z均不为零),求的值.
26.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
27.三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.
(1)在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);
(2)△BCD是不是黄金三角形?如果是,请给出证明;如果不是,请说明理由;
(3)设,试求k的值;
(4)如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,请直接写出的值.
参考答案与试题解析
一.选择题
1.解:∵=,
∴设x=3k,y=2k(k≠0),
∴==.
故选:A.
2.解:设实际距离为xcm,则:
1:500000=25:x,
解得x=12500000.
12500000cm=125km.
故选:A.
3.解:由题意得:
∴=1.
即:S1=S2.
故选:A.
4.解:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD;AD∥BC,
∴==,而AB=CD,
∴==,而AB=CD,
∴==;
又∵AF∥BC,
∴=.
故选:A.
5.解:A、两个矩形,对应角相等,都是直角,但四条边不一定对应成比例,故本选项不符合题意;
B、两个等腰梯形,四个角不一定对应相等,边也不一定对应成比例,所以不一定相似,故本选项不符合题意;
C、两个菱形,有一个角相等,则其它角也对应相等,而四条边都相等,所以对应成比例,所以相似,故本选项符合题意;
D、对应边成比例,对应角不一定相等,所以不一定相似,故本选项不符合题意.
故选:C.
6.解:因为角的度数和它的两边的长短无关,所以得到的新三角形应该是直角三角形,故选B.
7.解:,则==,
故选:D.
8.解:∵在△ABC中,DE∥BC,
∴△ADE∽△ABC,
∴,
∵,
∴=,
即=,
∵DE=4cm,
∴BC=12cm.
故选:B.
9.解:∵△ABC∽△DAC,
∴∠DAC=∠B=36°,∠BAC=∠D=117°,
∴∠BAD=∠DAC+∠BAC=153°,
故选:D.
10.解:由若===k,得
2b+c=ak,2c+a=bk,2a+b=ck,
三式相加,得3(a+b+c)=k(a+b+c)
由于a、b、c均不为0,且a+b+c≠0,
所以k==3.
故选:D.
二.填空题
11.解:∵x:y:z=1:2:3,
∴设x=t,y=2t,z=3t,
∵x﹣2y+3z=4,
∴t﹣4t+9t=4,
解得t=,
∴x﹣y+z=t﹣2t+3t=2t=2×=.
故答案为.
12.解:∵2a=3b,
∴a:b=3:2.
故答案为:3:2.
13.解:设A、B两地间的实际距离为xcm,由题意,得
1:500000=6:x,
解得x=3000000cm=30km.
故答案为30.
14.解:由一个图形到另一个图形,在改变的过程中形状不变,大小产生变化,属于相似变化.
15.解:∵从图1到图2,图形形状没变,只是大小发生改变,
∴从图1到图2的变换是相似变换.
故答案为:相似,
16.解:作DF∥AE交BC于F,如图,
∵OE∥DF,
∴==1,
即BE=EF,
∵DF∥AE,
∴==,
∴CF=2EF,
∴BE:EC=BE:3BE=1:3.
故答案为1:3.
17.解:∵=,
∴=,
设a=2t,b=3t,
∴==.
故答案为.
18.解:由于P为线段AB=4的黄金分割点,
且AP是较长线段;
则AP=AB=×4=2﹣2.
故答案为2﹣2.
19.解:∵CD∥EF
∴OD:OF=OC:OE
∵OC=3,CE=4
∴OD:OF=OC:OE=3:7.
20.解:∵Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB=10,
∵D是AB边的中点,
∴CD=BD=AB=5,
∵以D、C、P为顶点的三角形与△ABC相似,
∴∠DPC=90°或∠CDP=90°,
(1)若∠DPC=90°,则DP∥AC,
∴=,
∴BP=BC=4,
则PC=4;
(2)若∠CDP=90°,则△CDP∽△BCA,
∴,
即,
∴PC=.
∴PC=4或.
三.解答题
21.解:(1)∵FE∥CD,
∴=,即=,
解得,AC=,
则CE=AC﹣AE=﹣4=;
(2)∵DE∥BC,
∴=,即=,
解得,AB=.
22.解:(1)∵=,
∴=,
∴=,
(2)设===k,
则a=2k,b=3k,c=4k,
∵a+b+c=27,
∴2k+3k+4k=27,
∴k=3,
∴a=6,b=9,c=12.
23.解:设===k≠0,
则x=2k,y=3k,z=4k,
所以,===﹣3.
24.解:∵AB=7,BD=2,
∴AD=AB﹣BD=5.
∵DE∥BC,
∴=.
∵AE=6,
∴=,
∴AC=.
25.解:设=k,则x=6k,y=4k,z=3k
∴===3.
26.解:(1)路线图(6分)(P、A、C点各2分)
注意:起点是必须在所给的图形中画,否则即使画图正确扣;(2分)
(2)量得∠PAC≈105°,∠ACP≈45°;(9分)(只有1个正确得2分)
(3)量路线图得AC≈3.5厘米,PC≈6.8厘米.
∴AC≈3.5千米;PC≈6.8千米(13分)
27.解:(1)如图所示;
(2)△BCD是黄金三角形.
证明如下:∵点D在AB的垂直平分线上,
∴AD=BD,
∴∠ABD=∠A.
∵∠A=36°,AB=AC,
∴∠ABC=∠C=72°,
∴∠ABD=∠DBC=36°.
又∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴△BCD是黄金三角形.
(3)设BC=x,AC=y,
由(2)知,AD=BD=BC=x.
∵∠DBC=∠A,∠C=∠C,
∴△BDC∽△ABC,
∴,即,
整理,得x2+xy﹣y2=0,
解得.
因为x、y均为正数,所以.
(4).
理由:延长BC到E,使CE=AC,连接AE.
∵∠A=36°,AB=AC,
∴∠ACB=∠B=72°,
∴∠ACE=180°﹣72°=108°,
∴∠ACE=∠B1A1C1.
∵A1B1=AB,
∴AC=CE=A1B1=A1C1,
∴△ACE≌△B1A1C1,
∴AE=B1C1.
由(3)知,
∴,,
∴.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
