江西省吉安市吉水二高2020-2021学年高一下学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 江西省吉安市吉水二高2020-2021学年高一下学期期中考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 746.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 19:43:08 | ||
图片预览


文档简介
吉水二高2020-2021学年高一下学期期中考试
数学试卷
一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的代号填在答卷的相应表格内)
1. 下列命题中,正确的是( )
A.若,则 B.若,则
C.若,,则 D.若,则
2.从编号为01,02,…,49,50的50个个体中利用下面的随机数表选取5个个体,选取方法是从随机数表第1行第5列的数开始由左到右依次选取,则选出来的第5个个体的编号为( )
7816 6572 0812 1463[ 0872 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
A.08 B.14 C.28 D.43
3.某奶茶店的日销售收入y(单位:百元)与当天平均气温x(单位:)之间的关系如下:
x
0 1 2
y 5 ? 2 2 1
通过上面的五组数据得到了x与y之间的线性回归方程:;但是现在丢失了一个数据,该数据应为( )
A.2 B.3 C.4 D.5
4. 某校为了了解高一年级名新生的身体素质,将这些学生编号为,用系统抽样的方法抽出名学生进行体质测试,若编号为,,,,的名学生中有名没有被抽到,则这个编号是( )
A. B. C. D.
5.在中,,,则的值为( )
A. B. C.2 D.3
6.已知函数,则不等式的解集是( )
A. B. C. D.
7. “悦跑圈”是一款基于社交型的跑步应用,用户通过该平台可查看自己某时间段的运动情况,某人根据年月至年月期间每月跑步的里程(单位:十公里)的数据绘制了下面的折线图,根据该折线图,下列结论正确的是( )
A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为月份对应的里程数
D.月至月的月跑步里程相对于月至月波动性更小,变化比较平稳
8. 若关于的不等式的解集为,则不等式的解集是( )
A.{或} B.{或}
C. D.或
9.若正实数,满足,则的最小值为( )
A. B. C. D.5
10.若两个正实数,满足,且不等式恒成立,则实数的取值范围( )
A. B. C. D.
11. 设样本数据的平均数为,方差为,若数据的平均数比方差大,则的最大值为( )
A. B. C. D.
12.高斯函数,也称为取整函数,即表示不超过x的最大整数. 如: 已知正项数列的前项和为,且满足,则( ).
A.3 B.14 C.15 D.16
二、填空题(本大题共4小题,每小题5分,共20分,请将正确答案填写在横线上)
13. 某公司16个销售店某月销售产品数量(单位:台)的茎叶图如右图,
已知数据落在中的频率为0.25,则这组数据的中位数为_____.
14. 把一数列依次按第一个括号内一个数,第二个括号内两个数,第三个括号内三个数,第四个括号内一个数,…循环分为
则第50个括号内各数之和为__________.
15. 在中,角所对的边分别为, 的平分线交于点,且,则的最小值为_____.
16. 设,,是三个正实数,且,则的最大值为______.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
在中,内角A,B,C的对边分别为a,b,c,且.
(1)求A; (2)若,且的面积为,求的周长.
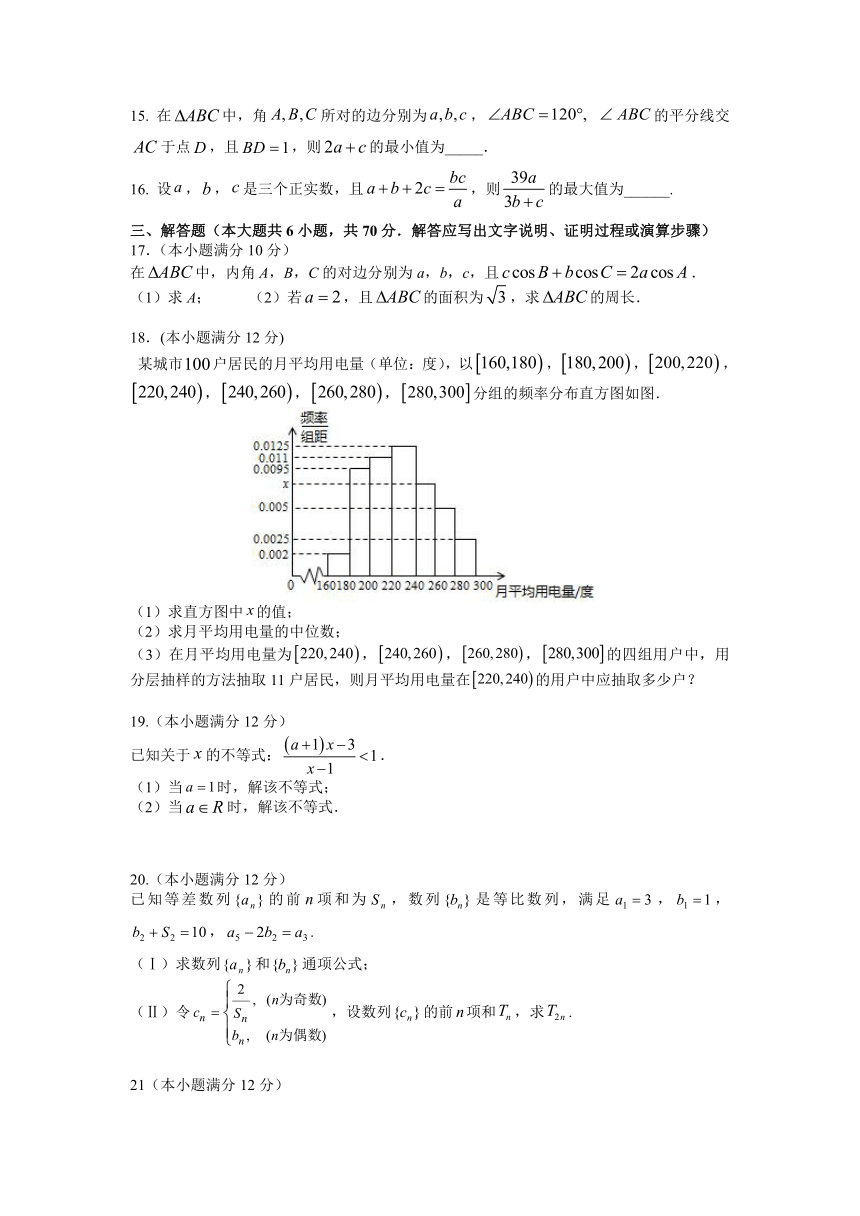
18.(本小题满分12分)
某城市户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求月平均用电量的中位数;
(3)在月平均用电量为,,,的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在的用户中应抽取多少户?
19.(本小题满分12分)
已知关于的不等式:.
(1)当时,解该不等式;
(2)当时,解该不等式.
20.(本小题满分12分)
已知等差数列的前项和为,数列是等比数列,满足,,,.
(Ⅰ)求数列和通项公式;
(Ⅱ)令,设数列的前项和,求.
21(本小题满分12分)
某固定在墙上的广告金属支架如图所示,根据要求,长要超过4米(不含4米),为的中点,到的距离比的长小1米,
(1)若,将支架的总长度表示为的函数,并写出函数的定义域.(注:支架的总长度为图中线段、和的长度之和)
(2)如何设计的长,可使支架总长度最短.
22.(本小题满分12分)
若函数对定义域内的每一个值,在其定义域内都存在唯一的,使成立,则称该函数为“依赖函数”.
(1)判断函数是否为“依赖函数”,并说明理由;
(2)若函数在定义域上为“依赖函数”,求的取值范围;
(3)已知函数在定义域上为“依赖函数”,若存在实数,使得对任意的,不等式都成立,求实数的最大值.
吉水二高2020-2021学年高一下学期期中考试
数学参考答案
一、选择题:本题共12小题,每小题5分,共60分。
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D C B C A B C A D B D B
二、填空题:本题共4小题,每小题5分,共20分。
13. 27 14. 392 15. 16. 3
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤。
17.解:(1)
(2)余弦定理知:
18. 解: (1)由直方图的性质得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:x=0.0075.
(2)因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,
设中位数为a,由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5得:a=224,所以月平均用电量的中位数是224.
(3)月平均用电量为[220,240)的用户有0.0125×20×100=25户,
月平均用电量为[240,260)的用户有0.0075×20×100=15户,
月平均用电量为[260,280)的用户有0. 005×20×100=10户,
月平均用电量为[280,300]用户有0.0025×20×100=5户,
抽取比例==,所以月平均用电量在[220,240)的用户抽取25×=5户.
19.解:(1)当时,原不等式可化为即,
故,所以,故原不等式的解为.
(2)原不等式可化为即,
当时,不等式的解为或;
当时,原不等式可化为即;
当时,原不等式可化为,
若,则不等式的解为;
若,则不等式的解为;
若,则不等式的解为.
综上,当时,不等式的解为,当时,不等式的解为,
当时,不等式的解为,当时,不等式的解为,
当时,不等式的解为.
20.解:(1)设的公差为d,公比为q
21.解: (1)由,则,设,
则支架的总长度为,
在中,由余弦定理
化简得 即 ①
记 由,则
由题中条件得
(2)设
则原式
∵由基本不等式 ∴
有且仅当,即时成立,又由满足
∴,∴当时,金属支架总长度最短.
22.解:(1)对于函数的定义域内存在,则无解,
故不是“依赖函数”.
(2)因为在上递增,故,即,,
由,故,得,
从而在上单调递增,故.
(3)①若,故在上最小值为0,此时不存在,舍去;
②若,故在上单调递减,
从而,解得(舍)或,
从而存在.使得对任意的,有不等式都成立,
即恒成立,
由,得.
由,可得,
又在单调递减,故当时,,
从而,解得,
综上,故实数的最大值为.
数学试卷
一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的代号填在答卷的相应表格内)
1. 下列命题中,正确的是( )
A.若,则 B.若,则
C.若,,则 D.若,则
2.从编号为01,02,…,49,50的50个个体中利用下面的随机数表选取5个个体,选取方法是从随机数表第1行第5列的数开始由左到右依次选取,则选出来的第5个个体的编号为( )
7816 6572 0812 1463[ 0872 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
A.08 B.14 C.28 D.43
3.某奶茶店的日销售收入y(单位:百元)与当天平均气温x(单位:)之间的关系如下:
x
0 1 2
y 5 ? 2 2 1
通过上面的五组数据得到了x与y之间的线性回归方程:;但是现在丢失了一个数据,该数据应为( )
A.2 B.3 C.4 D.5
4. 某校为了了解高一年级名新生的身体素质,将这些学生编号为,用系统抽样的方法抽出名学生进行体质测试,若编号为,,,,的名学生中有名没有被抽到,则这个编号是( )
A. B. C. D.
5.在中,,,则的值为( )
A. B. C.2 D.3
6.已知函数,则不等式的解集是( )
A. B. C. D.
7. “悦跑圈”是一款基于社交型的跑步应用,用户通过该平台可查看自己某时间段的运动情况,某人根据年月至年月期间每月跑步的里程(单位:十公里)的数据绘制了下面的折线图,根据该折线图,下列结论正确的是( )
A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为月份对应的里程数
D.月至月的月跑步里程相对于月至月波动性更小,变化比较平稳
8. 若关于的不等式的解集为,则不等式的解集是( )
A.{或} B.{或}
C. D.或
9.若正实数,满足,则的最小值为( )
A. B. C. D.5
10.若两个正实数,满足,且不等式恒成立,则实数的取值范围( )
A. B. C. D.
11. 设样本数据的平均数为,方差为,若数据的平均数比方差大,则的最大值为( )
A. B. C. D.
12.高斯函数,也称为取整函数,即表示不超过x的最大整数. 如: 已知正项数列的前项和为,且满足,则( ).
A.3 B.14 C.15 D.16
二、填空题(本大题共4小题,每小题5分,共20分,请将正确答案填写在横线上)
13. 某公司16个销售店某月销售产品数量(单位:台)的茎叶图如右图,
已知数据落在中的频率为0.25,则这组数据的中位数为_____.
14. 把一数列依次按第一个括号内一个数,第二个括号内两个数,第三个括号内三个数,第四个括号内一个数,…循环分为
则第50个括号内各数之和为__________.
15. 在中,角所对的边分别为, 的平分线交于点,且,则的最小值为_____.
16. 设,,是三个正实数,且,则的最大值为______.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
在中,内角A,B,C的对边分别为a,b,c,且.
(1)求A; (2)若,且的面积为,求的周长.
18.(本小题满分12分)
某城市户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求月平均用电量的中位数;
(3)在月平均用电量为,,,的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在的用户中应抽取多少户?
19.(本小题满分12分)
已知关于的不等式:.
(1)当时,解该不等式;
(2)当时,解该不等式.
20.(本小题满分12分)
已知等差数列的前项和为,数列是等比数列,满足,,,.
(Ⅰ)求数列和通项公式;
(Ⅱ)令,设数列的前项和,求.
21(本小题满分12分)
某固定在墙上的广告金属支架如图所示,根据要求,长要超过4米(不含4米),为的中点,到的距离比的长小1米,
(1)若,将支架的总长度表示为的函数,并写出函数的定义域.(注:支架的总长度为图中线段、和的长度之和)
(2)如何设计的长,可使支架总长度最短.
22.(本小题满分12分)
若函数对定义域内的每一个值,在其定义域内都存在唯一的,使成立,则称该函数为“依赖函数”.
(1)判断函数是否为“依赖函数”,并说明理由;
(2)若函数在定义域上为“依赖函数”,求的取值范围;
(3)已知函数在定义域上为“依赖函数”,若存在实数,使得对任意的,不等式都成立,求实数的最大值.
吉水二高2020-2021学年高一下学期期中考试
数学参考答案
一、选择题:本题共12小题,每小题5分,共60分。
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D C B C A B C A D B D B
二、填空题:本题共4小题,每小题5分,共20分。
13. 27 14. 392 15. 16. 3
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤。
17.解:(1)
(2)余弦定理知:
18. 解: (1)由直方图的性质得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:x=0.0075.
(2)因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,
设中位数为a,由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5得:a=224,所以月平均用电量的中位数是224.
(3)月平均用电量为[220,240)的用户有0.0125×20×100=25户,
月平均用电量为[240,260)的用户有0.0075×20×100=15户,
月平均用电量为[260,280)的用户有0. 005×20×100=10户,
月平均用电量为[280,300]用户有0.0025×20×100=5户,
抽取比例==,所以月平均用电量在[220,240)的用户抽取25×=5户.
19.解:(1)当时,原不等式可化为即,
故,所以,故原不等式的解为.
(2)原不等式可化为即,
当时,不等式的解为或;
当时,原不等式可化为即;
当时,原不等式可化为,
若,则不等式的解为;
若,则不等式的解为;
若,则不等式的解为.
综上,当时,不等式的解为,当时,不等式的解为,
当时,不等式的解为,当时,不等式的解为,
当时,不等式的解为.
20.解:(1)设的公差为d,公比为q
21.解: (1)由,则,设,
则支架的总长度为,
在中,由余弦定理
化简得 即 ①
记 由,则
由题中条件得
(2)设
则原式
∵由基本不等式 ∴
有且仅当,即时成立,又由满足
∴,∴当时,金属支架总长度最短.
22.解:(1)对于函数的定义域内存在,则无解,
故不是“依赖函数”.
(2)因为在上递增,故,即,,
由,故,得,
从而在上单调递增,故.
(3)①若,故在上最小值为0,此时不存在,舍去;
②若,故在上单调递减,
从而,解得(舍)或,
从而存在.使得对任意的,有不等式都成立,
即恒成立,
由,得.
由,可得,
又在单调递减,故当时,,
从而,解得,
综上,故实数的最大值为.
同课章节目录
