2021-2022学年沪科版数学九年级上册第22章相似形单元测试自我综合评价(word解析版)
文档属性
| 名称 | 2021-2022学年沪科版数学九年级上册第22章相似形单元测试自我综合评价(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 246.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览


文档简介
第22章 相似形 自我综合评价(二)
一、选择题(每小题5分,共50分)
1.若=,则的值为
( )
A.
B.
C.
D.
2.如图1,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E与B,D,F.若AC=4,CE=6,BD=3,则DF的长是
( )
图1
A.4
B.4.5
C.5
D.5.5
3.已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的面积比是
( )
A.5∶3
B.25∶9
C.3∶5
D.9∶25
4.在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,下列条件不能判定它们相似的是
( )
A.∠A=∠B'
B.AC=BC,A'C'=B'C'
C.AB=3BC,A'B'=3B'C'
D.△ABC中有两边长为3,4,△A'B'C'中有两边长为6,8
5.如图2,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的,那么点B'的坐标是
( )
图2
A.(3,2)
B.(-2,-3)
C.(2,3)或(-2,-3)
D.(3,2)或(-3,-2)
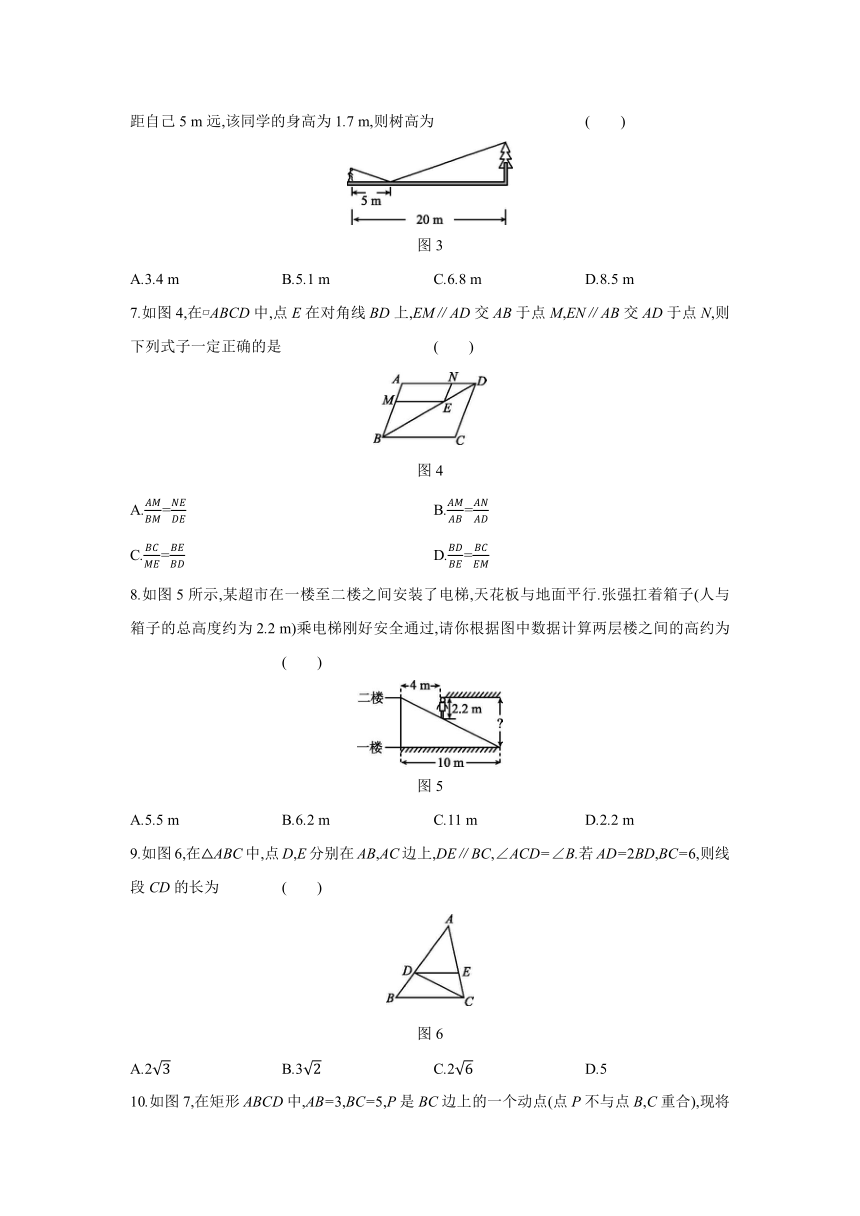
6.如图3,一同学在湖边看到一棵树,他目测出自己与树的距离为20
m,树的顶端在水中的倒影距自己5
m远,该同学的身高为1.7
m,则树高为
( )
图3
A.3.4
m
B.5.1
m
C.6.8
m
D.8.5
m
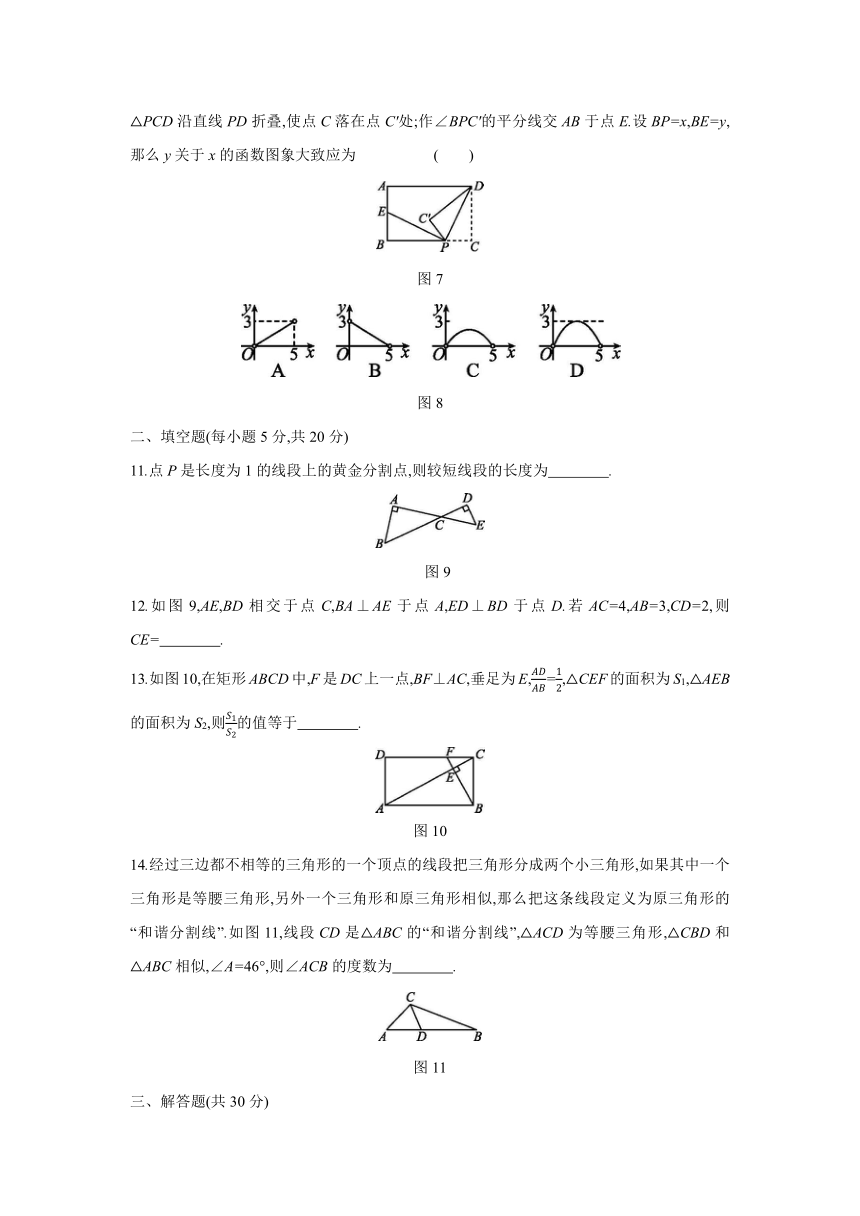
7.如图4,在?ABCD中,点E在对角线BD上,EM∥AD交AB于点M,EN∥AB交AD于点N,则下列式子一定正确的是
( )
图4
A.=
B.=
C.=
D.=
8.如图5所示,某超市在一楼至二楼之间安装了电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2
m)乘电梯刚好安全通过,请你根据图中数据计算两层楼之间的高约为
( )
图5
A.5.5
m
B.6.2
m
C.11
m
D.2.2
m
9.如图6,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B.若AD=2BD,BC=6,则线段CD的长为
( )
图6
A.2
B.3
C.2
D.5
10.如图7,在矩形ABCD中,AB=3,BC=5,P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落在点C'处;作∠BPC'的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为
( )
图7
图8
二、填空题(每小题5分,共20分)
11.点P是长度为1的线段上的黄金分割点,则较短线段的长度为 .?
图9
12.如图9,AE,BD相交于点C,BA⊥AE于点A,ED⊥BD于点D.若AC=4,AB=3,CD=2,则CE= .?
13.如图10,在矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,△CEF的面积为S1,△AEB的面积为S2,则的值等于 .?
图10
14.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个三角形是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图11,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为 .?
图11
三、解答题(共30分)
15.(8分)如图12,已知菱形AMNP内接于△ABC,点M,N,P分别在边AB,BC,AC上,如果AB=21
cm,CA=15
cm,求菱形AMNP的周长.
图12
16.(10分)如图13,在由边长为1的小正方形组成的网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(-1,2),B(2,1),C(4,5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出扩大后的△A2B2C2,使△A2B2C2与△ABC位似,且相似比为2.
图13
17.(12分)如图14,在△ABC中,AB=AC,P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
图14
教师详解详析
1.B [解析]
方法1:利用合比性质直接求出答案;方法2:设a=2k,b=3k,则==.故选B.
2.B [解析]
∵a∥b∥c,∴=,即=,解得DF=4.5.故选B.
3.B [解析]
∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴两三角形的相似比为5∶3,
则△ABC与△A'B'C'的面积比是25∶9.
故选B.
4.D
5.D [解析]
∵矩形OA'B'C'与矩形OABC关于点O位似,矩形OA'B'C'的面积等于矩形OABC面积的,
∴矩形OA'B'C'与矩形OABC的相似比是.
∵点B的坐标是(6,4),
∴点B'的坐标是(3,2)或(-3,-2).
故选D.
6.B [解析]
由题意可知,两直角三角形相似,设树高x
m,
由相似三角形的性质得=,
∴x=5.1
m.
故选B.
7.D [解析]
∵EN∥AB,EM∥AD,∴△BEM∽△BDA∽△EDN,∴==,A项错误;=,B项错误;==,C项错误;==,D项正确.故选D.
8.A
9.C [解析]
设AD=2x,则BD=x,∴AB=3x.∵DE∥BC,∴△ADE∽△ABC,∴==,∴=,∴DE=4,=.∵∠ACD=∠B,∠ADE=∠B,∴∠ADE=∠ACD.∵∠A=∠A,∴△ADE∽△ACD,∴==.设AE=2y,则AC=3y,∴=,∴AD=y,∴=,∴CD=2.故选C.
10.C [解析]
由翻折的性质,得∠CPD=∠C'PD.∵PE平分∠BPC',∴∠BPE=∠C'PE,∴∠BPE+∠CPD=90°.∵∠C=90°,∴∠CPD+∠PDC=90°,∴∠BPE=∠PDC.又∵∠B=∠C=90°,∴△PCD∽△EBP,∴=,即=,∴y=x(5-x)=-(x-)2+,故函数图象为C选项中的图象.
11. [解析]
较短线段的长度=1-=.
12.2.5 [解析]
∵BA⊥AE,AC=4,AB=3,∴BC==5.∵BA⊥AE,ED⊥BD,∴∠A=∠D=90°.又∵∠ACB=∠DCE,∴△ABC∽△DEC,∴=,即=,∴CE=2.5.故答案为2.5.
13. [解析]
∵=,∴设AD=BC=a,则AB=CD=2a,∴AC=a.∵BF⊥AC,∴△CBE∽△CAB,△AEB∽△ABC,∴=,=,即BC2=CE·AC,AB2=AE·AC,∴a2=CE·a,(2a)2=AE·a,∴CE=,AE=,
∴=.
∵△CEF∽△AEB,
∴=()2=.
故答案为.
14.113°或92° [解析]
∵△CBD∽△ABC,∴∠BCD=∠A=46°.∵△ACD是等腰三角形,∠ADC>∠BCD,∴∠ADC>∠A,即AC≠CD.①当AC=AD时,∠ACD=∠ADC=×(180°-46°)=67°,∴∠ACB=67°+46°=113°;②当DA=DC时,∠ACD=∠A=46°,∴∠ACB=46°+46°=92°.故答案为113°或92°.
15.解:∵四边形AMNP是菱形,
∴PN∥AB,PN=PA,
∴△CPN∽△CAB,
∴CP∶CA=PN∶AB.
∵PN=PA,∴CP∶CA=PA∶AB,
即CP∶15=PA∶21,
从而CP∶PA=15∶21=5∶7,
∴(CP+PA)∶PA=(5+7)∶7,
∴AC∶PA=12∶7,
即15∶PA=12∶7,
解得PA=,
∴菱形AMNP的周长是×4=35(cm).
16.解:(1)如图所示,△A1B1C1就是所求三角形.
(2)如图所示,△A2B2C2就是所求三角形.
17.解:(1)证明:∵∠APC=∠APD+∠DPC=∠PAB+∠B,且∠APD=∠B,
∴∠DPC=∠PAB.
又∵AB=AC,
∴∠ABP=∠PCD,∴△ABP∽△PCD,
∴=.
又∵AB=AC,∴=,
即AC·CD=CP·BP.
(2)∵PD∥AB,∴∠DPC=∠B.
由(1)中知∠DPC=∠PAB,
∴∠PAB=∠B.
又∵∠B=∠C,∴∠PAB=∠C.
又∵∠PBA=∠ABC,∴△PBA∽△ABC,
∴=,
∴BP===.
一、选择题(每小题5分,共50分)
1.若=,则的值为
( )
A.
B.
C.
D.
2.如图1,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E与B,D,F.若AC=4,CE=6,BD=3,则DF的长是
( )
图1
A.4
B.4.5
C.5
D.5.5
3.已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的面积比是
( )
A.5∶3
B.25∶9
C.3∶5
D.9∶25
4.在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,下列条件不能判定它们相似的是
( )
A.∠A=∠B'
B.AC=BC,A'C'=B'C'
C.AB=3BC,A'B'=3B'C'
D.△ABC中有两边长为3,4,△A'B'C'中有两边长为6,8
5.如图2,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的,那么点B'的坐标是
( )
图2
A.(3,2)
B.(-2,-3)
C.(2,3)或(-2,-3)
D.(3,2)或(-3,-2)
6.如图3,一同学在湖边看到一棵树,他目测出自己与树的距离为20
m,树的顶端在水中的倒影距自己5
m远,该同学的身高为1.7
m,则树高为
( )
图3
A.3.4
m
B.5.1
m
C.6.8
m
D.8.5
m
7.如图4,在?ABCD中,点E在对角线BD上,EM∥AD交AB于点M,EN∥AB交AD于点N,则下列式子一定正确的是
( )
图4
A.=
B.=
C.=
D.=
8.如图5所示,某超市在一楼至二楼之间安装了电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2
m)乘电梯刚好安全通过,请你根据图中数据计算两层楼之间的高约为
( )
图5
A.5.5
m
B.6.2
m
C.11
m
D.2.2
m
9.如图6,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B.若AD=2BD,BC=6,则线段CD的长为
( )
图6
A.2
B.3
C.2
D.5
10.如图7,在矩形ABCD中,AB=3,BC=5,P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落在点C'处;作∠BPC'的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为
( )
图7
图8
二、填空题(每小题5分,共20分)
11.点P是长度为1的线段上的黄金分割点,则较短线段的长度为 .?
图9
12.如图9,AE,BD相交于点C,BA⊥AE于点A,ED⊥BD于点D.若AC=4,AB=3,CD=2,则CE= .?
13.如图10,在矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,△CEF的面积为S1,△AEB的面积为S2,则的值等于 .?
图10
14.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个三角形是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图11,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为 .?
图11
三、解答题(共30分)
15.(8分)如图12,已知菱形AMNP内接于△ABC,点M,N,P分别在边AB,BC,AC上,如果AB=21
cm,CA=15
cm,求菱形AMNP的周长.
图12
16.(10分)如图13,在由边长为1的小正方形组成的网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(-1,2),B(2,1),C(4,5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出扩大后的△A2B2C2,使△A2B2C2与△ABC位似,且相似比为2.
图13
17.(12分)如图14,在△ABC中,AB=AC,P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
图14
教师详解详析
1.B [解析]
方法1:利用合比性质直接求出答案;方法2:设a=2k,b=3k,则==.故选B.
2.B [解析]
∵a∥b∥c,∴=,即=,解得DF=4.5.故选B.
3.B [解析]
∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴两三角形的相似比为5∶3,
则△ABC与△A'B'C'的面积比是25∶9.
故选B.
4.D
5.D [解析]
∵矩形OA'B'C'与矩形OABC关于点O位似,矩形OA'B'C'的面积等于矩形OABC面积的,
∴矩形OA'B'C'与矩形OABC的相似比是.
∵点B的坐标是(6,4),
∴点B'的坐标是(3,2)或(-3,-2).
故选D.
6.B [解析]
由题意可知,两直角三角形相似,设树高x
m,
由相似三角形的性质得=,
∴x=5.1
m.
故选B.
7.D [解析]
∵EN∥AB,EM∥AD,∴△BEM∽△BDA∽△EDN,∴==,A项错误;=,B项错误;==,C项错误;==,D项正确.故选D.
8.A
9.C [解析]
设AD=2x,则BD=x,∴AB=3x.∵DE∥BC,∴△ADE∽△ABC,∴==,∴=,∴DE=4,=.∵∠ACD=∠B,∠ADE=∠B,∴∠ADE=∠ACD.∵∠A=∠A,∴△ADE∽△ACD,∴==.设AE=2y,则AC=3y,∴=,∴AD=y,∴=,∴CD=2.故选C.
10.C [解析]
由翻折的性质,得∠CPD=∠C'PD.∵PE平分∠BPC',∴∠BPE=∠C'PE,∴∠BPE+∠CPD=90°.∵∠C=90°,∴∠CPD+∠PDC=90°,∴∠BPE=∠PDC.又∵∠B=∠C=90°,∴△PCD∽△EBP,∴=,即=,∴y=x(5-x)=-(x-)2+,故函数图象为C选项中的图象.
11. [解析]
较短线段的长度=1-=.
12.2.5 [解析]
∵BA⊥AE,AC=4,AB=3,∴BC==5.∵BA⊥AE,ED⊥BD,∴∠A=∠D=90°.又∵∠ACB=∠DCE,∴△ABC∽△DEC,∴=,即=,∴CE=2.5.故答案为2.5.
13. [解析]
∵=,∴设AD=BC=a,则AB=CD=2a,∴AC=a.∵BF⊥AC,∴△CBE∽△CAB,△AEB∽△ABC,∴=,=,即BC2=CE·AC,AB2=AE·AC,∴a2=CE·a,(2a)2=AE·a,∴CE=,AE=,
∴=.
∵△CEF∽△AEB,
∴=()2=.
故答案为.
14.113°或92° [解析]
∵△CBD∽△ABC,∴∠BCD=∠A=46°.∵△ACD是等腰三角形,∠ADC>∠BCD,∴∠ADC>∠A,即AC≠CD.①当AC=AD时,∠ACD=∠ADC=×(180°-46°)=67°,∴∠ACB=67°+46°=113°;②当DA=DC时,∠ACD=∠A=46°,∴∠ACB=46°+46°=92°.故答案为113°或92°.
15.解:∵四边形AMNP是菱形,
∴PN∥AB,PN=PA,
∴△CPN∽△CAB,
∴CP∶CA=PN∶AB.
∵PN=PA,∴CP∶CA=PA∶AB,
即CP∶15=PA∶21,
从而CP∶PA=15∶21=5∶7,
∴(CP+PA)∶PA=(5+7)∶7,
∴AC∶PA=12∶7,
即15∶PA=12∶7,
解得PA=,
∴菱形AMNP的周长是×4=35(cm).
16.解:(1)如图所示,△A1B1C1就是所求三角形.
(2)如图所示,△A2B2C2就是所求三角形.
17.解:(1)证明:∵∠APC=∠APD+∠DPC=∠PAB+∠B,且∠APD=∠B,
∴∠DPC=∠PAB.
又∵AB=AC,
∴∠ABP=∠PCD,∴△ABP∽△PCD,
∴=.
又∵AB=AC,∴=,
即AC·CD=CP·BP.
(2)∵PD∥AB,∴∠DPC=∠B.
由(1)中知∠DPC=∠PAB,
∴∠PAB=∠B.
又∵∠B=∠C,∴∠PAB=∠C.
又∵∠PBA=∠ABC,∴△PBA∽△ABC,
∴=,
∴BP===.
