2021-2022学年鲁教版(五四制)九年级数学上册《第2章直角三角形的边角关系》同步能力达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学上册《第2章直角三角形的边角关系》同步能力达标测评(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览




文档简介
2021年鲁教版九年级数学上册《第2章直角三角形的边角关系》
同步能力达标测评(附答案)
一.选择题(共10小题,满分30分,每小题3分)
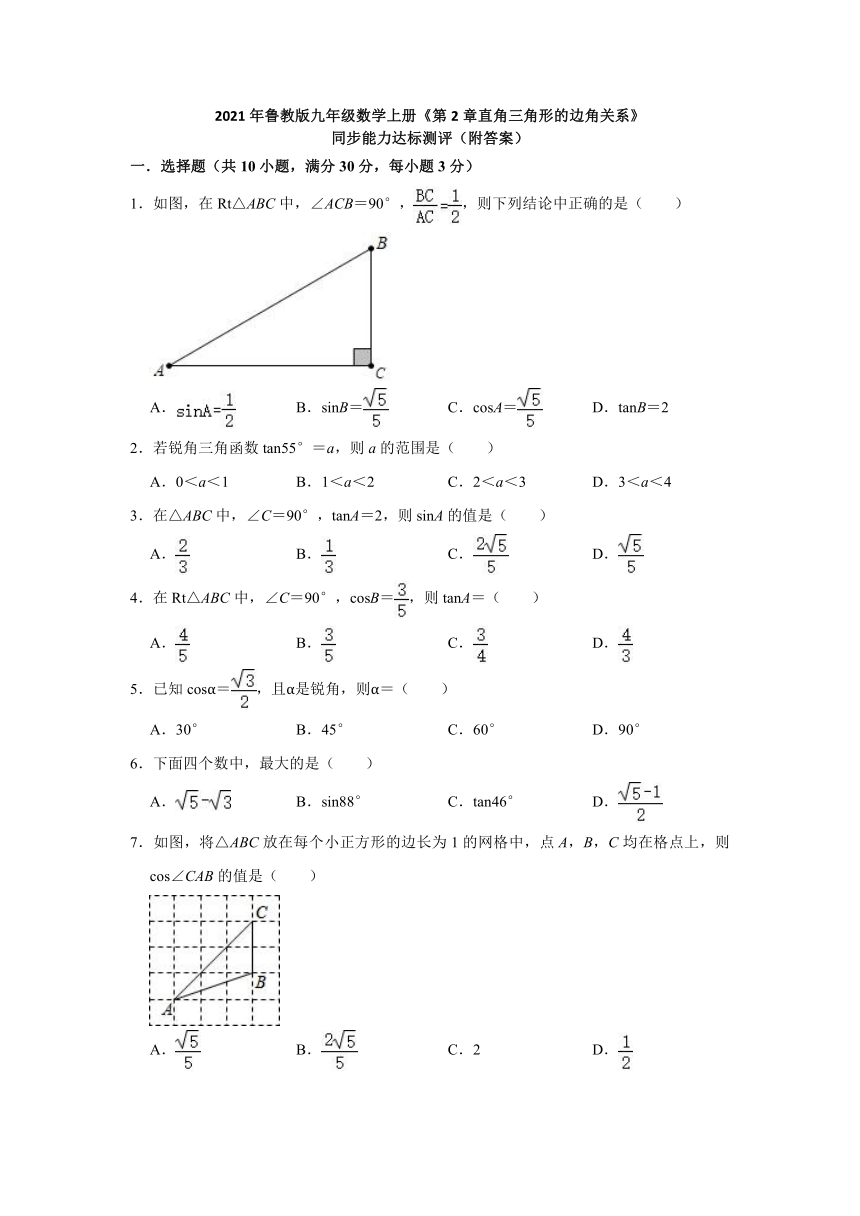
1.如图,在Rt△ABC中,∠ACB=90°,,则下列结论中正确的是( )
A.
B.sinB=
C.cosA=
D.tanB=2
2.若锐角三角函数tan55°=a,则a的范围是( )
A.0<a<1
B.1<a<2
C.2<a<3
D.3<a<4
3.在△ABC中,∠C=90°,tanA=2,则sinA的值是( )
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,cosB=,则tanA=( )
A.
B.
C.
D.
5.已知cosα=,且α是锐角,则α=( )
A.30°
B.45°
C.60°
D.90°
6.下面四个数中,最大的是( )
A.
B.sin88°
C.tan46°
D.
7.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则cos∠CAB的值是( )
A.
B.
C.2
D.
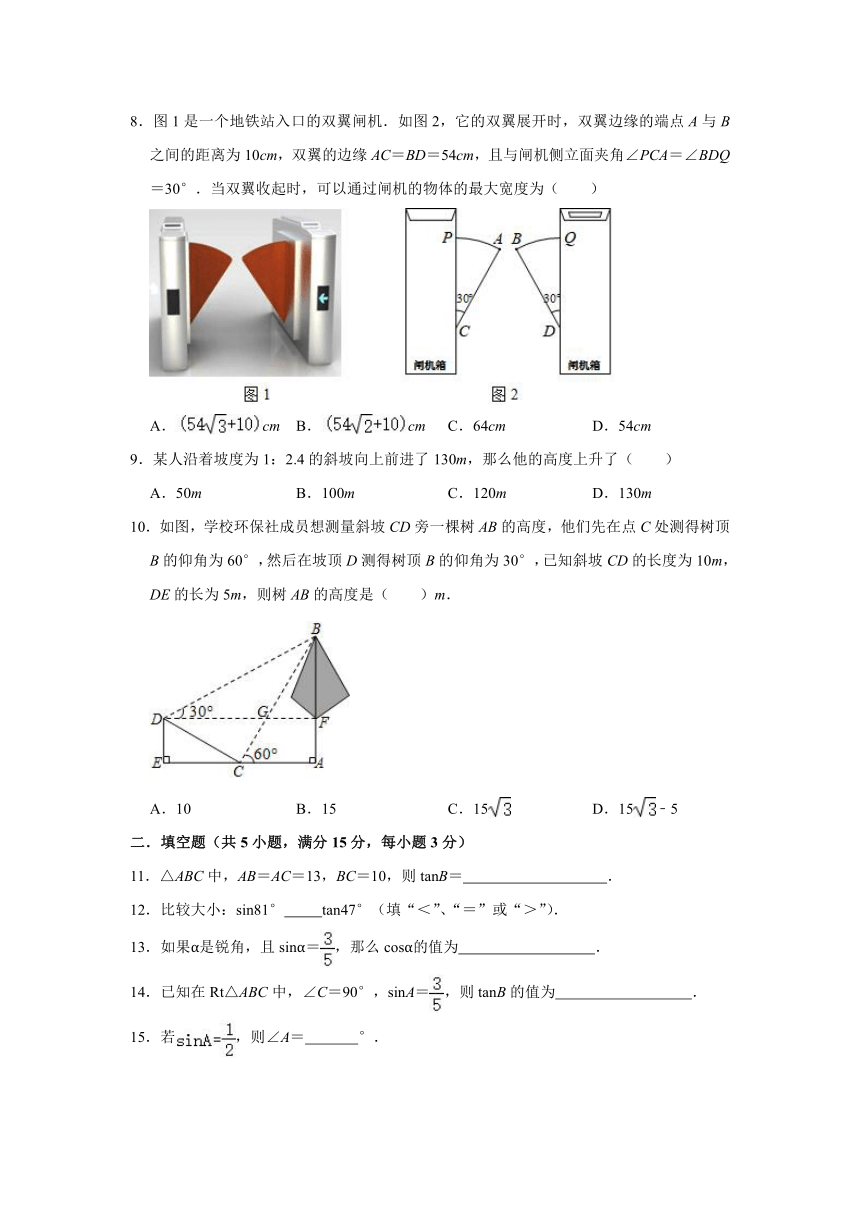
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.cm
B.cm
C.64cm
D.54cm
9.某人沿着坡度为1:2.4的斜坡向上前进了130m,那么他的高度上升了( )
A.50m
B.100m
C.120m
D.130m
10.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10
B.15
C.15
D.15﹣5
二.填空题(共5小题,满分15分,每小题3分)
11.△ABC中,AB=AC=13,BC=10,则tanB=
.
12.比较大小:sin81°
tan47°(填“<”、“=”或“>”).
13.如果α是锐角,且sinα=,那么cosα的值为
.
14.已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为
.
15.若,则∠A=
°.
三.解答题(共8小题,满分55分)
16.在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边.
(1)已知c=2,b=,求∠B;
(2)已知c=12,sinA=,求b.
17.计算:
(1)
(2)
(3)已知α为锐角,,计算的值.
18.计算:tan60°﹣2cos30°+sin45°.
19.如图,AC是△ABD的高,∠D=45°,∠B=60°,AD=10.求AB的长.
20.改革开放40年来,中国已经成为领先世界的基建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点F在线段HG上运动,BC∥HG,AE⊥BC,垂足为点E,AE的延长线交HG于点G,经测量,∠ABD=11°,∠ADE=26°,∠ACE=31°,BC=20m,EG=0.6m.
(1)求线段AG的长度;
(2)连接AF,当线段AF⊥AC时,求点F和点G之间的距离.
(所有结果精确到0.1m.参考数据:tan11°≈0.19,tan26°≈0.49,tan31°≈0.60)
21.如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出5m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.
22.如图,两座建筑物AB,DC的水平距离BC为30m,从点A测得点D的俯角为30°,测得点C的俯角为45°,求这两座建筑物的高度(结果保留根号).
23.如图,小明从P处出发,沿北偏东60°方向以70m/min的速度步行6min后到达A处,接着向正南方向步行一段时间后到达终点B处,在B处观测到出发时所在的P处在北偏西37°方向上.求小明步行的总路程(精确到1m).
参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.4,≈1.7.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵在Rt△ABC中,∠ACB=90°,,
∴设BC=x,则AC=2x,故AB=x,
故sinA===,故A选项错误;
sinB===,故B选项错误;
cosA===,故C选项错误;
tanB==2,故D选项正确;
故选:D.
2.解:∵tan45°=1,tan60°=,且锐角范围内tanα随∠α的增大而增大,
∴tan45°<tan55°<tan60°,即1<a<,
则1<a<2,
故选:B.
3.解:∵∠C=90°,
∴tanA==2,
设AC=x,则BC=2x,
∴AB==x,
∴sinA===.故选:C.
4.解:如图所示:∵∠C=90°,cosB=,
∴设BC=3x,则AB=5x,
故AC=4x,
则tanA==.
故选:C.
5.解:∵cosα=,且α是锐角,
∴α=30°.
故选:A.
6.解:A、﹣≈2.236﹣1.732≈0.504;
B、sin88°≈0.999;
C、tan46°≈1.036;
D、≈≈0.568.
故tan46°最大,
故选:C.
7.解:取格点D,E,连接BD,如图,
∵∠CDE=∠BDE=45°,
∴∠CDB=90°.
∵AD=,AB=,
∴在Rt△ADB中,cos∠CAB=.
故选:B.
8.解:如图所示,过A作AE⊥CP于E,过B作BF⊥DQ于F,则
Rt△ACE中,AE=AC=×54=27(cm),
同理可得,BF=27cm,
又∵点A与B之间的距离为10cm,
∴通过闸机的物体的最大宽度为27+10+27=64(cm),
故选:C.
9.解:如图,
根据题意知AB=130米,tanB==1:2.4,
设AC=x,则BC=2.4x,
则x2+(2.4x)2=1302,
解得x=50或x=﹣50(负值舍去),
即他的高度上升了50m,
故选:A.
10.解:在Rt△CDE中,
∵CD=10m,DE=5m,
∴sin∠DCE=,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===10(m),
∴AB=BC?sin60°=10×=15(m).
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:如图,等腰△ABC中,AB=AC=13,BC=10,
过A作AD⊥BC于D,则BD=5,
在Rt△ABD中,AB=13,BD=5,则,
AD==12,
故tanB==.
故答案为.
12.解:∵sin81°<sin90°=1,tan47°>tan45°=1,
∴sin81°<1<tan47°,
∴sin81°<tan47°.
故答案为<.
13.解:∵sin2α+cos2α=1,sinα=,
∴+cos2α=1,
∴cos2α=,
∵α是锐角,
∴cosα=,
故答案为:.
14.解:∵在Rt△ABC中,∠C=90°,sinA=,
∴sinA==,
设a为3k,则c为5k,
根据勾股定理可得:b=4k,
∴tanB==,
故答案为:.
15.解:∵sinA=,
∴∠A=30°,
故答案为:30.
三.解答题(共8小题,满分55分)
16.解:(1)∵sinB===,
∴∠B=45°;
(2)∵c=12,sinA==,
∴a=4,
∴b==8,
17.解:(1)原式=3﹣1+=2+=.
(2)原式=4﹣2×1+5=4﹣2+5=7.
(3)∵α为锐角,,
∴α﹣15°=45°.
∴α=60°.
∴
=﹣2×+3×﹣2
=﹣1+3﹣2
=﹣1+.
18.解:原式=﹣2×+
=﹣+
=.
19.解:在Rt△ACD中,AC=ADsinD=10sin45°=5,
在Rt△ABC中,AB===.
20.解:(1)设AE=x,
∵tan∠ABE=,tan∠ACE=,
∴BE=,CE=
∵BE+CE=BC,
∴+=20,
∴解得:x≈2.9,
∴AG=2.9+0.6=3.5m;
(2)当AF⊥AC时,
∴∠FAG+∠EAC=∠EAC+∠ACE=90°,
∴∠FAG=∠ACE=31°,
∴tan31°=,
∴FG≈2.1.
21.解:(1)在Rt△ABD中,∠ABD=45°,
∴AD=AB=4(m),
在Rt△ACD中,∠ACD=30°,
∴AC=2AD=8(m),
答:新传送带AC的长度为8m;
(2)在Rt△ACD中,∠ACD=30°,
∴CD=AB?cos∠ACD=4(m),
在Rt△ABD中,∠ABD=45°,
∴BD=AD=4(m),
∴BC=CD﹣BD=(4﹣4)m,
∴PC=BP﹣BC=4﹣(4﹣4)=4(m),
∵4<5,
∴货物MNQP需要挪走.
22.解:过点A作AE⊥CD,交CD的延长线于E,
则四边形ABCE是矩形,
∴AE∥BC,AE=BC,AB=CE,∠ACB=∠CAE=45°,
在Rt△ABC中,∵∠ACB=45°,
∴AB=BC=30米,
在Rt△AED中,DE=AE?tan30°=10米,
∴CD=CE﹣DE=AB﹣DE=(30﹣10)米,
答:建筑物AB高30米,建筑物CD高(30﹣10)米.
23.解:过点P作PC⊥AB于点C,
由题意得:PA=70×6=420,∠APC=30°,∠B=37°,
在Rt△PAC中,∠APC=30°,
∴AC=PA=210,PC=AP?cos∠APC≈420×=210,
在Rt△BPC中,tanB=,
则BC==≈485,
∴小明步行的总路程=PA+AB=420+210+485=1115(m).
同步能力达标测评(附答案)
一.选择题(共10小题,满分30分,每小题3分)
1.如图,在Rt△ABC中,∠ACB=90°,,则下列结论中正确的是( )
A.
B.sinB=
C.cosA=
D.tanB=2
2.若锐角三角函数tan55°=a,则a的范围是( )
A.0<a<1
B.1<a<2
C.2<a<3
D.3<a<4
3.在△ABC中,∠C=90°,tanA=2,则sinA的值是( )
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,cosB=,则tanA=( )
A.
B.
C.
D.
5.已知cosα=,且α是锐角,则α=( )
A.30°
B.45°
C.60°
D.90°
6.下面四个数中,最大的是( )
A.
B.sin88°
C.tan46°
D.
7.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则cos∠CAB的值是( )
A.
B.
C.2
D.
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.cm
B.cm
C.64cm
D.54cm
9.某人沿着坡度为1:2.4的斜坡向上前进了130m,那么他的高度上升了( )
A.50m
B.100m
C.120m
D.130m
10.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10
B.15
C.15
D.15﹣5
二.填空题(共5小题,满分15分,每小题3分)
11.△ABC中,AB=AC=13,BC=10,则tanB=
.
12.比较大小:sin81°
tan47°(填“<”、“=”或“>”).
13.如果α是锐角,且sinα=,那么cosα的值为
.
14.已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为
.
15.若,则∠A=
°.
三.解答题(共8小题,满分55分)
16.在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边.
(1)已知c=2,b=,求∠B;
(2)已知c=12,sinA=,求b.
17.计算:
(1)
(2)
(3)已知α为锐角,,计算的值.
18.计算:tan60°﹣2cos30°+sin45°.
19.如图,AC是△ABD的高,∠D=45°,∠B=60°,AD=10.求AB的长.
20.改革开放40年来,中国已经成为领先世界的基建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点F在线段HG上运动,BC∥HG,AE⊥BC,垂足为点E,AE的延长线交HG于点G,经测量,∠ABD=11°,∠ADE=26°,∠ACE=31°,BC=20m,EG=0.6m.
(1)求线段AG的长度;
(2)连接AF,当线段AF⊥AC时,求点F和点G之间的距离.
(所有结果精确到0.1m.参考数据:tan11°≈0.19,tan26°≈0.49,tan31°≈0.60)
21.如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出5m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.
22.如图,两座建筑物AB,DC的水平距离BC为30m,从点A测得点D的俯角为30°,测得点C的俯角为45°,求这两座建筑物的高度(结果保留根号).
23.如图,小明从P处出发,沿北偏东60°方向以70m/min的速度步行6min后到达A处,接着向正南方向步行一段时间后到达终点B处,在B处观测到出发时所在的P处在北偏西37°方向上.求小明步行的总路程(精确到1m).
参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.4,≈1.7.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵在Rt△ABC中,∠ACB=90°,,
∴设BC=x,则AC=2x,故AB=x,
故sinA===,故A选项错误;
sinB===,故B选项错误;
cosA===,故C选项错误;
tanB==2,故D选项正确;
故选:D.
2.解:∵tan45°=1,tan60°=,且锐角范围内tanα随∠α的增大而增大,
∴tan45°<tan55°<tan60°,即1<a<,
则1<a<2,
故选:B.
3.解:∵∠C=90°,
∴tanA==2,
设AC=x,则BC=2x,
∴AB==x,
∴sinA===.故选:C.
4.解:如图所示:∵∠C=90°,cosB=,
∴设BC=3x,则AB=5x,
故AC=4x,
则tanA==.
故选:C.
5.解:∵cosα=,且α是锐角,
∴α=30°.
故选:A.
6.解:A、﹣≈2.236﹣1.732≈0.504;
B、sin88°≈0.999;
C、tan46°≈1.036;
D、≈≈0.568.
故tan46°最大,
故选:C.
7.解:取格点D,E,连接BD,如图,
∵∠CDE=∠BDE=45°,
∴∠CDB=90°.
∵AD=,AB=,
∴在Rt△ADB中,cos∠CAB=.
故选:B.
8.解:如图所示,过A作AE⊥CP于E,过B作BF⊥DQ于F,则
Rt△ACE中,AE=AC=×54=27(cm),
同理可得,BF=27cm,
又∵点A与B之间的距离为10cm,
∴通过闸机的物体的最大宽度为27+10+27=64(cm),
故选:C.
9.解:如图,
根据题意知AB=130米,tanB==1:2.4,
设AC=x,则BC=2.4x,
则x2+(2.4x)2=1302,
解得x=50或x=﹣50(负值舍去),
即他的高度上升了50m,
故选:A.
10.解:在Rt△CDE中,
∵CD=10m,DE=5m,
∴sin∠DCE=,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===10(m),
∴AB=BC?sin60°=10×=15(m).
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:如图,等腰△ABC中,AB=AC=13,BC=10,
过A作AD⊥BC于D,则BD=5,
在Rt△ABD中,AB=13,BD=5,则,
AD==12,
故tanB==.
故答案为.
12.解:∵sin81°<sin90°=1,tan47°>tan45°=1,
∴sin81°<1<tan47°,
∴sin81°<tan47°.
故答案为<.
13.解:∵sin2α+cos2α=1,sinα=,
∴+cos2α=1,
∴cos2α=,
∵α是锐角,
∴cosα=,
故答案为:.
14.解:∵在Rt△ABC中,∠C=90°,sinA=,
∴sinA==,
设a为3k,则c为5k,
根据勾股定理可得:b=4k,
∴tanB==,
故答案为:.
15.解:∵sinA=,
∴∠A=30°,
故答案为:30.
三.解答题(共8小题,满分55分)
16.解:(1)∵sinB===,
∴∠B=45°;
(2)∵c=12,sinA==,
∴a=4,
∴b==8,
17.解:(1)原式=3﹣1+=2+=.
(2)原式=4﹣2×1+5=4﹣2+5=7.
(3)∵α为锐角,,
∴α﹣15°=45°.
∴α=60°.
∴
=﹣2×+3×﹣2
=﹣1+3﹣2
=﹣1+.
18.解:原式=﹣2×+
=﹣+
=.
19.解:在Rt△ACD中,AC=ADsinD=10sin45°=5,
在Rt△ABC中,AB===.
20.解:(1)设AE=x,
∵tan∠ABE=,tan∠ACE=,
∴BE=,CE=
∵BE+CE=BC,
∴+=20,
∴解得:x≈2.9,
∴AG=2.9+0.6=3.5m;
(2)当AF⊥AC时,
∴∠FAG+∠EAC=∠EAC+∠ACE=90°,
∴∠FAG=∠ACE=31°,
∴tan31°=,
∴FG≈2.1.
21.解:(1)在Rt△ABD中,∠ABD=45°,
∴AD=AB=4(m),
在Rt△ACD中,∠ACD=30°,
∴AC=2AD=8(m),
答:新传送带AC的长度为8m;
(2)在Rt△ACD中,∠ACD=30°,
∴CD=AB?cos∠ACD=4(m),
在Rt△ABD中,∠ABD=45°,
∴BD=AD=4(m),
∴BC=CD﹣BD=(4﹣4)m,
∴PC=BP﹣BC=4﹣(4﹣4)=4(m),
∵4<5,
∴货物MNQP需要挪走.
22.解:过点A作AE⊥CD,交CD的延长线于E,
则四边形ABCE是矩形,
∴AE∥BC,AE=BC,AB=CE,∠ACB=∠CAE=45°,
在Rt△ABC中,∵∠ACB=45°,
∴AB=BC=30米,
在Rt△AED中,DE=AE?tan30°=10米,
∴CD=CE﹣DE=AB﹣DE=(30﹣10)米,
答:建筑物AB高30米,建筑物CD高(30﹣10)米.
23.解:过点P作PC⊥AB于点C,
由题意得:PA=70×6=420,∠APC=30°,∠B=37°,
在Rt△PAC中,∠APC=30°,
∴AC=PA=210,PC=AP?cos∠APC≈420×=210,
在Rt△BPC中,tanB=,
则BC==≈485,
∴小明步行的总路程=PA+AB=420+210+485=1115(m).
