《2.6应用一元二次方程》同步能力提升训练(附答案)2021-2022学年九年级数学北师大版上册
文档属性
| 名称 | 《2.6应用一元二次方程》同步能力提升训练(附答案)2021-2022学年九年级数学北师大版上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 469.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览




文档简介
2021年北师大版九年级数学上册《2.6应用一元二次方程》同步能力提升训练(附答案)
1.电影《我和我的祖国》一上映,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若增长率记作x,方程可以列为( )
A.3(1+x)=10 B.3 (1+x)2=10
C.3+3(1+x)2=10 D.3+3(1+x)+3(1+x)2=10
2.从盛满20升纯酒精的容器里倒出若干升,然后用水注满,再倒出同样升数的混合液后,这时容器里剩下纯酒精5升.则每次倒出溶液的升数为( )
A.5 B.6 C.8 D.10
3.在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡张,设参加活动的同学有人,根据题意,可列方程( )
A. B. C. D.
4.某小区附近新建一个游泳馆,馆内矩形游泳池的面积为,且游泳池的宽比长短.设游泳池的长为,则可列方程为( )
A. B.
C. D.
5.将一个正方形剪成①、②、③、④四块(如图1),恰能拼成如图2的矩形,若,则这个正方形的面积为( )
A. B. C.9 D.
6.一个菱形两条对角线的长是方程的两个根,则该菱形的面积为( )
A.12 B.6或12 C.8 D.6
7.某种商品,平均每天可销售40件,每件盈利20元.若每件减价1元,则每天可多销售10件.如果每天要盈利1400元,且每件的利润不得低于12元,那么每件应降价_____元.
8.美丽乡村建设中,某村2019年新增绿化面积为20000平方米,计划到2021年新增绿化面积要达到28800平方米.如果每年新增绿化面积的增长率相同,这个增长率是________.
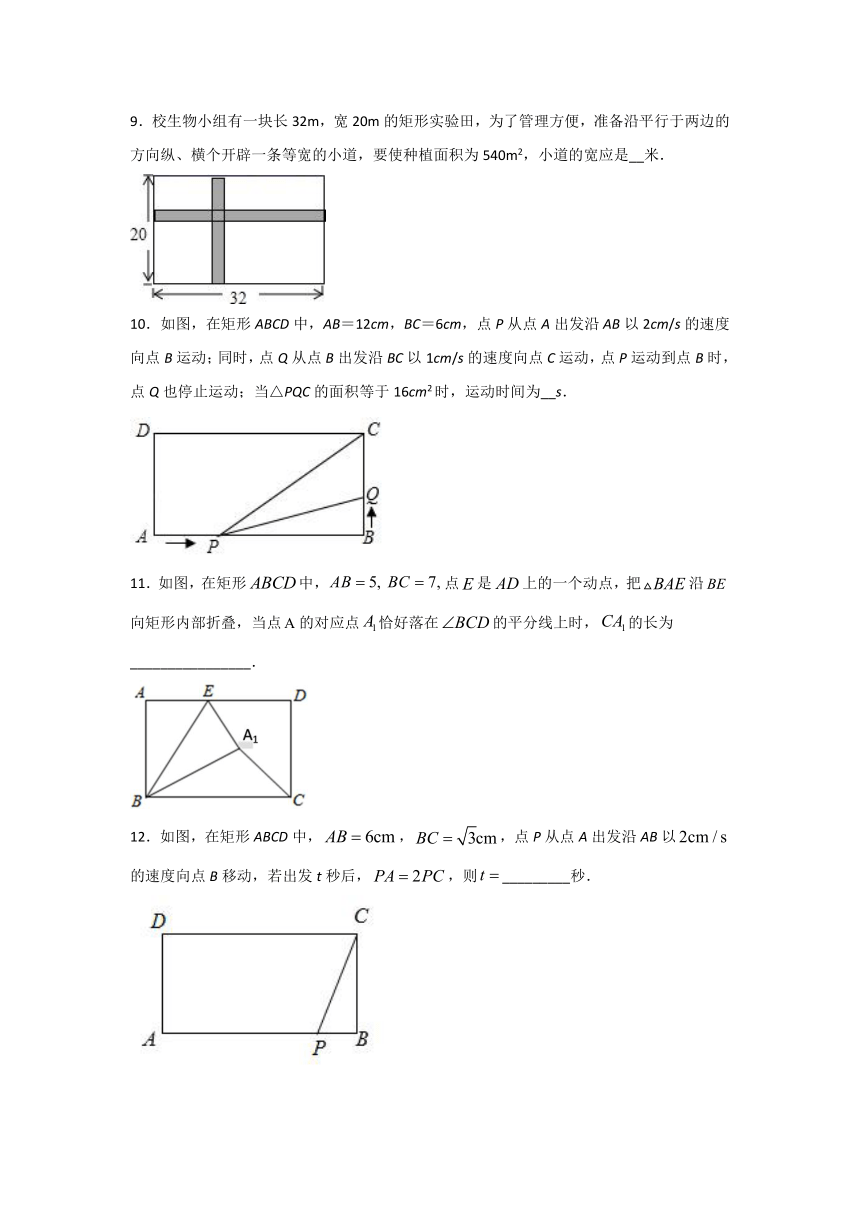
9.校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横个开辟一条等宽的小道,要使种植面积为540m2,小道的宽应是__米.
10.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P从点A出发沿AB以2cm/s的速度向点B运动;同时,点Q从点B出发沿BC以1cm/s的速度向点C运动,点P运动到点B时,点Q也停止运动;当△PQC的面积等于16cm2时,运动时间为__s.
11.如图,在矩形中,点是上的一个动点,把沿向矩形内部折叠,当点的对应点恰好落在的平分线上时,的长为________________.
12.如图,在矩形ABCD中,,,点P从点A出发沿AB以的速度向点B移动,若出发t秒后,,则_________秒.
13.如图,一次函数的图象交x轴于点A,交y轴于点B,点E在线段上(不与点A,B重合),过点E分别作和的垂线,垂足为C,D.当矩形的面积为1时,点E的坐标为_________.
14.为响应“把中国人的饭碗牢牢端在自己手中”的号召,确保粮食安全,优选品种,提高产量,某农业科技小组对原有的玉米品种进行改良种植研究.在保持去年种植面积不变的情况下,预计玉米平均亩产量将在去年的基础上增加.因为优化了品种,预计每千克售价将在去年的基础上上涨,全部售出后预计总收入将增加.求的值.
15.小北在夜市摆摊卖牛仔裤,2020年5月以50元/条的进价购进牛仔裤400条,以80元/条的售价全部售完.到了6月,为了提高销量,小北决定降价促销,经调研发现:每条牛仔裤的售价在5月售价基础上每降价1元,月销量就会相应增加25条.
(1)若小北6月计划销售牛仔裤750条,则牛仔裤6月的售价应定为多少元?
(2)实际上,6月牛仔裤的进价比5月便宜了,而实际售价在5月基础上降了m元,且购进的牛仔裤全部售完,已知小北6月的总利润比5月增加了,求m的值.
16.某商店经销甲、乙两种商品,已知两种商品的进价之和是3元,甲商品零售价比进价多一元.乙商品零售价比进价的2倍少1元,按零售价购买3件甲和2件乙商品共花费12元.
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进价分别为______元和______元;甲、乙两种商品的零售价分别为______元和______元(直接写出答案).
(2)该商店平均每天卖出甲商品500件和乙商品1200件,经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件.求解当甲商品售价定为多少时,才能使商店每天销售甲、乙两种商品获取的利润共1700元?
17.如图,中,∠C=90°,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以2cm/s的速度移动,在B点停止.(1)如果点P,Q分别从A、C同时出发,经过几秒钟,使?
(2)如果点P从点A先出发2s,点Q再从点C出发,经过几秒钟后?
(3)如果点P、Q分别从A、C同时出发,经过几秒钟后PQ=BQ?
18.如图,用一面足够长的墙为一边,其余三边用总长米的围栏建两个面积相同的生态园,由于场地限制,垂直于墙的一边长不超过米.(围栏宽忽略不计)
(1)每个生态园的面积为平方米,求每个生态园的边长;
(2)每个生态园的面积能否达到平方米?请说明理由.
19.某商贸公司10名销售员3月份完成的销售额情况如下表:
销售额(万元) 3 4 5 6 7 8 16
销售员人数 1 1 3 2 1 1 1
(1)销售额的中位数是_____万元,众数____万元,平均每人完成的销售额_____万元,.
(2)其中有位销售员甲3月份的销售额是8万元,计划到5月份增长到12.5万元,求每月的平均增长率.
20.2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.世界卫生组织提出:如果1人传播10人以上而且被传染的人已经确定为新冠肺炎,那么这个传播者就可以称为”超级传播者”.如果某地区有1人不幸成为新冠肺炎病毒的携带者,假设一个病毒携带者每轮传染的人数相同,经过两轮传染后共有81人成为新冠肺炎病毒的携带者.
(1)请判断最初的这名病毒携带者是”超级传播者”吗?求他每轮传染的人数;
(2)若不加以控制传染渠道,经过3轮传染,新冠肺炎病毒的携带者共有多少人?
参考答案
题号 1 2 3 4 5 6
答案 D D A A D D
7.6.
解:设每件降价x元,则平均每天可售出(40+10x)件,
依题意,得:(20-x)(40+10x)=1400,
整理,得:x2-16x+60=0,
解得:x1=6,x2=10.
∵每件的利润不得低于12元,
∴x=6,
故答案为:6.
8.20%
解:设这个增长率为x,由题意得
20000(1+x)2=28800,
(1+x)2=1.44,
1+x=±1.2,
所以x1=0.2,x2=-2.2(舍去),
故x=0.2=20%.
故答案是:20%.
9.2
解:设道路的宽为xm,依题意有
(32﹣x)(20﹣x)=540,
整理,得x2﹣52x+100=0,
∴(x﹣50)(x﹣2)=0,
∴x1=2,x2=50(不合题意,舍去),
答:小道的宽应是2m.
故答案为:2.
10.2.
解:设运动时间为xs(0≤x≤6),则PB=(12﹣2x)cm,CQ=(6﹣x)cm,
依题意,得:(12﹣2x)(6﹣x)=16,
整理,得:x2﹣12x+20=0,
解得:x1=2,x2=10(不合题意,舍去).
故答案为:2.
11.或
解:过点A1作A1F⊥BC于F
∵四边形ABCD为矩形,平分
∴
∴△为等腰直角三角形,设CF==x
则BF=BC-CF=7-x,CA1==
由折叠的性质可得AB==5
在Rt△中,
即
解得:x1=3,x2=4
∴CA1=或
故答案为:或.
12.4-
解:∵在矩形ABCD中,,,点P从点A出发沿AB以的速度向点B移动,
∴PA=2t,PC=,
∵,
∴2t=,解得:t1=4-,t2=4+(舍去),
故答案是:4-.
13.或
解:对于一次函数,
当时,,解得,则,
由题意,设点的坐标为,则,
当矩形的面积为1时,
则,
解得或,均符合题意,
当时,,则,
当时,,则,
综上,点的坐标为或,
故答案为:或.
14.10.
解:根据题意可得:
解之得: ,(不合题意,舍去)
.
15.(1)66元;(2)m=8.
解:(1)设牛仔裤6月的售价应定为x元,则由题意可得:
400+25×(80-x)=750,
解之得:x=66
答:牛仔裤6月的售价应定为66元;
(2)由题意可得:
,
解之得:m=8或m=0(舍去),
∴m=8.
16.(1)甲、乙零售价分别为2元和3元;(2)甲售价1.5元.
(1)设甲进价为元,乙进价为元
解得:,
∴
∴甲、乙的进价分别为1元和2元
甲、乙的零售价分别为2元和3元
故答案为:1,2;2,3;
(2)设甲降价元,则每天销售件,
解得:(舍),,
∴甲售价1.5元.
17.(1)2或4;(2)2;(3).
解:(1)P、Q同时出发,经过秒钟,,
由题意得:
∴,
解得:,.
经2秒点P到离A点1×2=2cm处,点Q离C点2×2=4cm处,经4秒点P到离A点1×4=4cm处,点Q到离C点2×4=8cm处,经验证,它们都符合要求.
答:P、Q同时出发,经过2秒或4秒,.
(2)设P出发t秒时,则Q运动的时间为秒,由题意得:
,
∴,
解得:.
因此经4秒点P离A点1×4=4cm,点Q离C点2×(4﹣2)=4cm,符合题意.
答:P先出发2秒,Q再从C出发,经过2秒后.
(3)设经过秒钟后PQ=BQ,则,,,
,
解得:,(不合题意,舍去),
答:经过秒钟后PQ=BQ.
18.(1)生态园的垂直于墙的一边长为4米,另一边长为12米;(2)不能;
解:(1)设生态园垂直于墙的一边长为x米由题意得方程:
整理得
解得,(由x不能大于6,将其舍去)
∴生态园另一边长为(米)
答:生态园的垂直于墙的一边长为4米,另一边长为12米;
(2)假设每个生态园的面积可以为60平方米,设生态园垂直于墙的一边长为x米由题意得方程:
整理得
此一元二次方程的判别式
所以原方程无解,
所以每个生态园的面积不可能达到60平方米.
19.(1)5.5万元;5万元;6.5万元;(2)
解:(1)∵共有10人,
∴中位数应该是排序后第5和第6人的平均数,
∴中位数为=5.5(万元);
销售额为5万的有3人,最多,
所以销售额的众数为5万元;
平均销售额为:(3+4+3×5+6×2+7+8+16)=6.5(万元);
(2)设每月的平均增长率为x,
由题意可得:
8(1+x)2=12.5,
解得:x=0.25或x=-2.25(舍),
∴每月的平均增长率为25%.
20.(1)不是;8人;(2)729人
解:(1)设每人每轮传染人,
依题意,得:,得:,(不合题意,舍去),
又∵ 8<10,∴最初的这名病毒携带者不是“超级传播者”;
所以最初这名病毒携带者不是“超级传播者”;他每轮传染的人数8人;
(2)81×(1+8)=729(人),
所以若不加以控制传染渠道,经过3轮传染,共有729人成为新冠肺炎病毒的携带者
1.电影《我和我的祖国》一上映,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若增长率记作x,方程可以列为( )
A.3(1+x)=10 B.3 (1+x)2=10
C.3+3(1+x)2=10 D.3+3(1+x)+3(1+x)2=10
2.从盛满20升纯酒精的容器里倒出若干升,然后用水注满,再倒出同样升数的混合液后,这时容器里剩下纯酒精5升.则每次倒出溶液的升数为( )
A.5 B.6 C.8 D.10
3.在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡张,设参加活动的同学有人,根据题意,可列方程( )
A. B. C. D.
4.某小区附近新建一个游泳馆,馆内矩形游泳池的面积为,且游泳池的宽比长短.设游泳池的长为,则可列方程为( )
A. B.
C. D.
5.将一个正方形剪成①、②、③、④四块(如图1),恰能拼成如图2的矩形,若,则这个正方形的面积为( )
A. B. C.9 D.
6.一个菱形两条对角线的长是方程的两个根,则该菱形的面积为( )
A.12 B.6或12 C.8 D.6
7.某种商品,平均每天可销售40件,每件盈利20元.若每件减价1元,则每天可多销售10件.如果每天要盈利1400元,且每件的利润不得低于12元,那么每件应降价_____元.
8.美丽乡村建设中,某村2019年新增绿化面积为20000平方米,计划到2021年新增绿化面积要达到28800平方米.如果每年新增绿化面积的增长率相同,这个增长率是________.
9.校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横个开辟一条等宽的小道,要使种植面积为540m2,小道的宽应是__米.
10.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P从点A出发沿AB以2cm/s的速度向点B运动;同时,点Q从点B出发沿BC以1cm/s的速度向点C运动,点P运动到点B时,点Q也停止运动;当△PQC的面积等于16cm2时,运动时间为__s.
11.如图,在矩形中,点是上的一个动点,把沿向矩形内部折叠,当点的对应点恰好落在的平分线上时,的长为________________.
12.如图,在矩形ABCD中,,,点P从点A出发沿AB以的速度向点B移动,若出发t秒后,,则_________秒.
13.如图,一次函数的图象交x轴于点A,交y轴于点B,点E在线段上(不与点A,B重合),过点E分别作和的垂线,垂足为C,D.当矩形的面积为1时,点E的坐标为_________.
14.为响应“把中国人的饭碗牢牢端在自己手中”的号召,确保粮食安全,优选品种,提高产量,某农业科技小组对原有的玉米品种进行改良种植研究.在保持去年种植面积不变的情况下,预计玉米平均亩产量将在去年的基础上增加.因为优化了品种,预计每千克售价将在去年的基础上上涨,全部售出后预计总收入将增加.求的值.
15.小北在夜市摆摊卖牛仔裤,2020年5月以50元/条的进价购进牛仔裤400条,以80元/条的售价全部售完.到了6月,为了提高销量,小北决定降价促销,经调研发现:每条牛仔裤的售价在5月售价基础上每降价1元,月销量就会相应增加25条.
(1)若小北6月计划销售牛仔裤750条,则牛仔裤6月的售价应定为多少元?
(2)实际上,6月牛仔裤的进价比5月便宜了,而实际售价在5月基础上降了m元,且购进的牛仔裤全部售完,已知小北6月的总利润比5月增加了,求m的值.
16.某商店经销甲、乙两种商品,已知两种商品的进价之和是3元,甲商品零售价比进价多一元.乙商品零售价比进价的2倍少1元,按零售价购买3件甲和2件乙商品共花费12元.
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进价分别为______元和______元;甲、乙两种商品的零售价分别为______元和______元(直接写出答案).
(2)该商店平均每天卖出甲商品500件和乙商品1200件,经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件.求解当甲商品售价定为多少时,才能使商店每天销售甲、乙两种商品获取的利润共1700元?
17.如图,中,∠C=90°,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以2cm/s的速度移动,在B点停止.(1)如果点P,Q分别从A、C同时出发,经过几秒钟,使?
(2)如果点P从点A先出发2s,点Q再从点C出发,经过几秒钟后?
(3)如果点P、Q分别从A、C同时出发,经过几秒钟后PQ=BQ?
18.如图,用一面足够长的墙为一边,其余三边用总长米的围栏建两个面积相同的生态园,由于场地限制,垂直于墙的一边长不超过米.(围栏宽忽略不计)
(1)每个生态园的面积为平方米,求每个生态园的边长;
(2)每个生态园的面积能否达到平方米?请说明理由.
19.某商贸公司10名销售员3月份完成的销售额情况如下表:
销售额(万元) 3 4 5 6 7 8 16
销售员人数 1 1 3 2 1 1 1
(1)销售额的中位数是_____万元,众数____万元,平均每人完成的销售额_____万元,.
(2)其中有位销售员甲3月份的销售额是8万元,计划到5月份增长到12.5万元,求每月的平均增长率.
20.2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.世界卫生组织提出:如果1人传播10人以上而且被传染的人已经确定为新冠肺炎,那么这个传播者就可以称为”超级传播者”.如果某地区有1人不幸成为新冠肺炎病毒的携带者,假设一个病毒携带者每轮传染的人数相同,经过两轮传染后共有81人成为新冠肺炎病毒的携带者.
(1)请判断最初的这名病毒携带者是”超级传播者”吗?求他每轮传染的人数;
(2)若不加以控制传染渠道,经过3轮传染,新冠肺炎病毒的携带者共有多少人?
参考答案
题号 1 2 3 4 5 6
答案 D D A A D D
7.6.
解:设每件降价x元,则平均每天可售出(40+10x)件,
依题意,得:(20-x)(40+10x)=1400,
整理,得:x2-16x+60=0,
解得:x1=6,x2=10.
∵每件的利润不得低于12元,
∴x=6,
故答案为:6.
8.20%
解:设这个增长率为x,由题意得
20000(1+x)2=28800,
(1+x)2=1.44,
1+x=±1.2,
所以x1=0.2,x2=-2.2(舍去),
故x=0.2=20%.
故答案是:20%.
9.2
解:设道路的宽为xm,依题意有
(32﹣x)(20﹣x)=540,
整理,得x2﹣52x+100=0,
∴(x﹣50)(x﹣2)=0,
∴x1=2,x2=50(不合题意,舍去),
答:小道的宽应是2m.
故答案为:2.
10.2.
解:设运动时间为xs(0≤x≤6),则PB=(12﹣2x)cm,CQ=(6﹣x)cm,
依题意,得:(12﹣2x)(6﹣x)=16,
整理,得:x2﹣12x+20=0,
解得:x1=2,x2=10(不合题意,舍去).
故答案为:2.
11.或
解:过点A1作A1F⊥BC于F
∵四边形ABCD为矩形,平分
∴
∴△为等腰直角三角形,设CF==x
则BF=BC-CF=7-x,CA1==
由折叠的性质可得AB==5
在Rt△中,
即
解得:x1=3,x2=4
∴CA1=或
故答案为:或.
12.4-
解:∵在矩形ABCD中,,,点P从点A出发沿AB以的速度向点B移动,
∴PA=2t,PC=,
∵,
∴2t=,解得:t1=4-,t2=4+(舍去),
故答案是:4-.
13.或
解:对于一次函数,
当时,,解得,则,
由题意,设点的坐标为,则,
当矩形的面积为1时,
则,
解得或,均符合题意,
当时,,则,
当时,,则,
综上,点的坐标为或,
故答案为:或.
14.10.
解:根据题意可得:
解之得: ,(不合题意,舍去)
.
15.(1)66元;(2)m=8.
解:(1)设牛仔裤6月的售价应定为x元,则由题意可得:
400+25×(80-x)=750,
解之得:x=66
答:牛仔裤6月的售价应定为66元;
(2)由题意可得:
,
解之得:m=8或m=0(舍去),
∴m=8.
16.(1)甲、乙零售价分别为2元和3元;(2)甲售价1.5元.
(1)设甲进价为元,乙进价为元
解得:,
∴
∴甲、乙的进价分别为1元和2元
甲、乙的零售价分别为2元和3元
故答案为:1,2;2,3;
(2)设甲降价元,则每天销售件,
解得:(舍),,
∴甲售价1.5元.
17.(1)2或4;(2)2;(3).
解:(1)P、Q同时出发,经过秒钟,,
由题意得:
∴,
解得:,.
经2秒点P到离A点1×2=2cm处,点Q离C点2×2=4cm处,经4秒点P到离A点1×4=4cm处,点Q到离C点2×4=8cm处,经验证,它们都符合要求.
答:P、Q同时出发,经过2秒或4秒,.
(2)设P出发t秒时,则Q运动的时间为秒,由题意得:
,
∴,
解得:.
因此经4秒点P离A点1×4=4cm,点Q离C点2×(4﹣2)=4cm,符合题意.
答:P先出发2秒,Q再从C出发,经过2秒后.
(3)设经过秒钟后PQ=BQ,则,,,
,
解得:,(不合题意,舍去),
答:经过秒钟后PQ=BQ.
18.(1)生态园的垂直于墙的一边长为4米,另一边长为12米;(2)不能;
解:(1)设生态园垂直于墙的一边长为x米由题意得方程:
整理得
解得,(由x不能大于6,将其舍去)
∴生态园另一边长为(米)
答:生态园的垂直于墙的一边长为4米,另一边长为12米;
(2)假设每个生态园的面积可以为60平方米,设生态园垂直于墙的一边长为x米由题意得方程:
整理得
此一元二次方程的判别式
所以原方程无解,
所以每个生态园的面积不可能达到60平方米.
19.(1)5.5万元;5万元;6.5万元;(2)
解:(1)∵共有10人,
∴中位数应该是排序后第5和第6人的平均数,
∴中位数为=5.5(万元);
销售额为5万的有3人,最多,
所以销售额的众数为5万元;
平均销售额为:(3+4+3×5+6×2+7+8+16)=6.5(万元);
(2)设每月的平均增长率为x,
由题意可得:
8(1+x)2=12.5,
解得:x=0.25或x=-2.25(舍),
∴每月的平均增长率为25%.
20.(1)不是;8人;(2)729人
解:(1)设每人每轮传染人,
依题意,得:,得:,(不合题意,舍去),
又∵ 8<10,∴最初的这名病毒携带者不是“超级传播者”;
所以最初这名病毒携带者不是“超级传播者”;他每轮传染的人数8人;
(2)81×(1+8)=729(人),
所以若不加以控制传染渠道,经过3轮传染,共有729人成为新冠肺炎病毒的携带者
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
