5.3应用一元一次方程——水箱变高了 同步提优训练 2021—2022学年北师大版数学七年级上册(Word版 含答案)
文档属性
| 名称 | 5.3应用一元一次方程——水箱变高了 同步提优训练 2021—2022学年北师大版数学七年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 357.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 13:09:12 | ||
图片预览


文档简介
3 应用一元一次方程——水箱变高了
命题点 1 用一元一次方程解决平面图形的周长与面积问题
1.用72 cm长的铁丝做一个长方形的教具,如果宽为15 cm,那么长为( )
A.28.5 cm B.42 cm C.21 cm D.33.5 cm
2.在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图1所示,求小长方形的宽.若设小长方形的宽为x cm,依题意可得方程( )
图1
A.6+2x=14-3x B.6+2x=x+(14-3x)
C.14-3x=6 D.6+2x=14-x
3.一块正方形铁皮,在每个角各截去一个一样的小正方形,折成底面边长是40 cm的无盖长方体盒子,其容积是24000 cm3,则原正方形铁皮的边长是________ cm.
4.如图2①是边长为40 cm的正方形纸板,裁掉阴影部分后将其折叠成如图②所示的长方体盒子,已知该长方体的宽与高相等,则这个长方体的体积为________cm3.
图2
5.如图3,一个长方形恰好分成6个正方形,其中最小的正方形的面积是1,求这个长方形的面积.
图3
命题点 2 用一元一次方程解决等长变形问题
6.如图4是一个用铁丝围成的梯形,将其改成一个长和宽的比为2∶1的长方形,那么该长方形的长和宽分别为多少?
图4
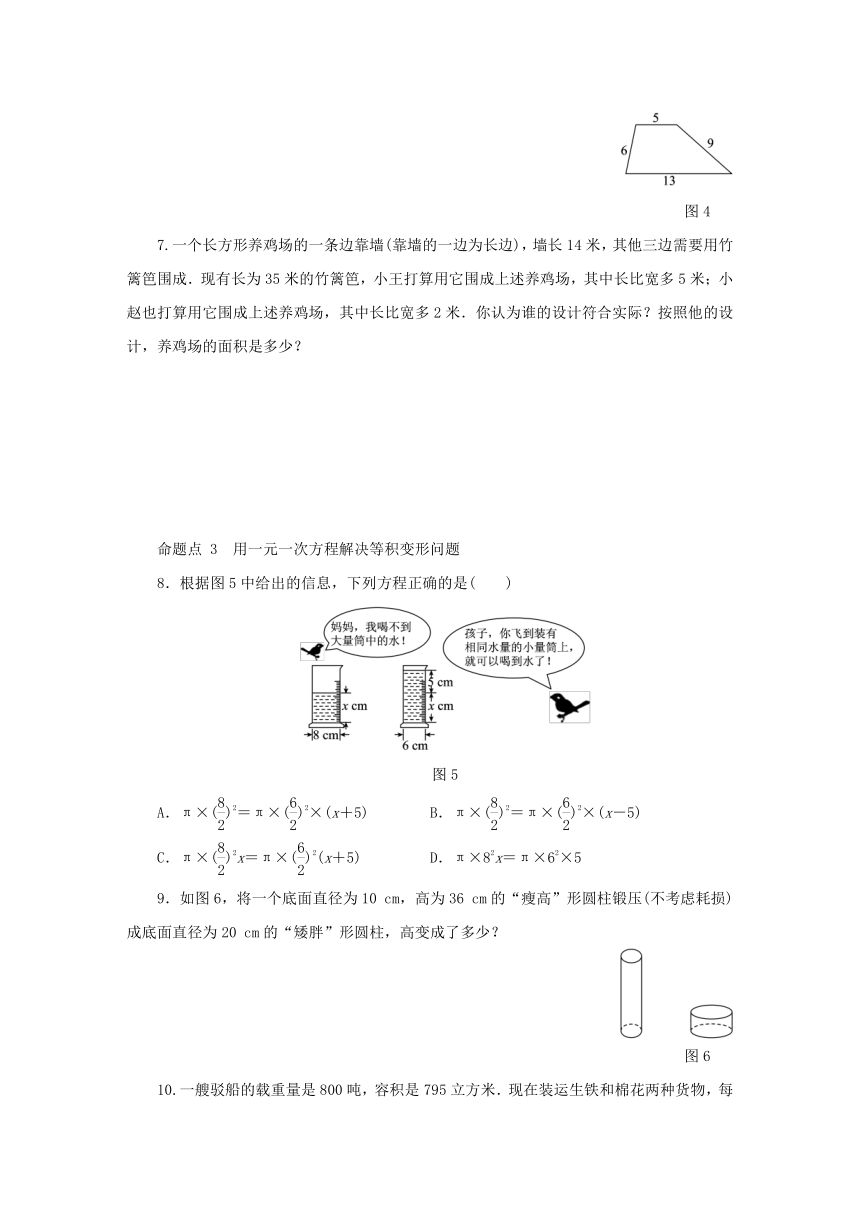
7.一个长方形养鸡场的一条边靠墙(靠墙的一边为长边),墙长14米,其他三边需要用竹篱笆围成.现有长为35米的竹篱笆,小王打算用它围成上述养鸡场,其中长比宽多5米;小赵也打算用它围成上述养鸡场,其中长比宽多2米.你认为谁的设计符合实际?按照他的设计,养鸡场的面积是多少?
命题点 3 用一元一次方程解决等积变形问题
8.根据图5中给出的信息,下列方程正确的是( )
图5
A.π×()2=π×()2×(x+5) B.π×()2=π×()2×(x-5)
C.π×()2x=π×()2(x+5) D.π×82x=π×62×5
9.如图6,将一个底面直径为10 cm,高为36 cm的“瘦高”形圆柱锻压(不考虑耗损)成底面直径为20 cm的“矮胖”形圆柱,高变成了多少?
图6
10.一艘驳船的载重量是800吨,容积是795立方米.现在装运生铁和棉花两种货物,每吨生铁的体积是0.3立方米,每吨棉花的体积是4立方米,为了充分利用船的载重量和容积,生铁和棉花各应装多少吨?
命题点 4 根据“表示同一个量的两个不同的式子相等”列方程解决问题
11.将一堆糖果分给幼儿园某班的小朋友,如果每人2颗,那么就多8颗,如果每人3颗,那么就少12颗.这个班有多少名小朋友?
12.某公路一侧原有路灯106盏(两端都有),相邻两盏灯之间的距离为36 m,为节约用电,现计划全部更换为新型节能灯,且相邻两盏灯之间的距离变为54 m,则需要更换新型节能灯多少盏?
13.在一个底面直径为2 cm,高为39 cm的量筒内装满水,再将量筒内的水倒入底面直径为4 cm,高为3 cm的3个烧杯内,能否完全装下?若装不下,量筒内的水还剩多高?
典题讲评与答案详析
1.C [解析] 设长方形的长为x cm,
根据题意,得2(x+15)=72,
解得x=21.
因此,长方形的长为21 cm.
2.B [解析] 小长方形的宽为x cm,则小长方形的长为(14-3x)cm.
根据题意,得6+2x=x+(14-3x).
3.70 [解析] 设剪去的小正方形的边长为x cm.
根据题意,得40×40×x=24000,
解得x=15.
所以原正方形的边长=40+2×15=70(cm).
4.2000 [解析] 设宽为x cm,则其高为=(20-x)cm.
根据题意,得x=20-x,
解得x=10.
故长方体的宽与高均为10 cm,长为40-10×2=20(cm),
所以长方体的体积为20×10×10=2000(cm3).5.[解析] 通过观察可发现6个正方形的边长间存在着数量关系.
将长方形的长用两种不同形式表示,从而建立等量关系.
解:如图,由最小的正方形的面积是1,可知最小的正方形的边长是1.设正方形①的边长为x,则正方形②的边长也为x,正方形③的边长为x+1,正方形④的边长为x+1+1,正方形⑤的边长为x+1+1+1.
根据题意,得x+1+2x=(x+1+1)+(x+1+1+1),解得x=4.
则长方形的长为13,宽为11.
故这个长方形的面积为13×11=143.
6.解:设长方形的宽为x,则长为2x.
根据题意,得2(x+2x)=5+6+13+9,
解得x=5.5.
2×5.5=11.
因此,该长方形的长为11,宽为5.5.
7.解:根据小王的设计可设宽为x米,则长为(x+5)米.根据题意,得2x+(x+5)=35,解得x=10.
因此小王设计的长方形养鸡场的长为10+5=15(米)>14米,故小王的设计不符合实际.
根据小赵的设计可设宽为y米,则长为(y+2)米.
根据题意,得2y+(y+2)=35,解得y=11.
因此小赵设计的长方形养鸡场的长为11+2=13(米)<14米,故小赵的设计符合实际.
按照他的设计,养鸡场的面积为11×13=143(米2).
8.C
9.解:设“矮胖”形圆柱的高变成了x cm.
根据题意,得()2π×36=()2π×x.
解得x=9.
因此,锻压后“矮胖”形圆柱的高变成了9 cm.
10.解:设生铁应装x吨,则棉花应装(800-x)吨.
根据题意,得0.3x+4(800-x)=795.
解得x=650.
800-650=150.
因此,生铁应装650吨,棉花应装150吨.
11.解:设这个班有x名小朋友.
根据题意,得2x+8=3x-12.解得x=20.
因此,这个班有20名小朋友.
12.解:设需要更换新型节能灯x盏.
根据题意,得(106-1)×36=(x-1)×54.
解得x=71.
因此,需要更换新型节能灯71盏.
13.解:V量筒=π×()2×39=39π(cm3),
V烧杯=π×()2×3=12π(cm3),
3×12π=36π(cm3).
因为39π>36π,
所以装不下.
设量筒内的水还剩x cm高.根据题意,得
π×()2×(39-x)=3×π×()2×3.
解得x=3.
即量筒内的水还剩3 cm高.
命题点 1 用一元一次方程解决平面图形的周长与面积问题
1.用72 cm长的铁丝做一个长方形的教具,如果宽为15 cm,那么长为( )
A.28.5 cm B.42 cm C.21 cm D.33.5 cm
2.在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图1所示,求小长方形的宽.若设小长方形的宽为x cm,依题意可得方程( )
图1
A.6+2x=14-3x B.6+2x=x+(14-3x)
C.14-3x=6 D.6+2x=14-x
3.一块正方形铁皮,在每个角各截去一个一样的小正方形,折成底面边长是40 cm的无盖长方体盒子,其容积是24000 cm3,则原正方形铁皮的边长是________ cm.
4.如图2①是边长为40 cm的正方形纸板,裁掉阴影部分后将其折叠成如图②所示的长方体盒子,已知该长方体的宽与高相等,则这个长方体的体积为________cm3.
图2
5.如图3,一个长方形恰好分成6个正方形,其中最小的正方形的面积是1,求这个长方形的面积.
图3
命题点 2 用一元一次方程解决等长变形问题
6.如图4是一个用铁丝围成的梯形,将其改成一个长和宽的比为2∶1的长方形,那么该长方形的长和宽分别为多少?
图4
7.一个长方形养鸡场的一条边靠墙(靠墙的一边为长边),墙长14米,其他三边需要用竹篱笆围成.现有长为35米的竹篱笆,小王打算用它围成上述养鸡场,其中长比宽多5米;小赵也打算用它围成上述养鸡场,其中长比宽多2米.你认为谁的设计符合实际?按照他的设计,养鸡场的面积是多少?
命题点 3 用一元一次方程解决等积变形问题
8.根据图5中给出的信息,下列方程正确的是( )
图5
A.π×()2=π×()2×(x+5) B.π×()2=π×()2×(x-5)
C.π×()2x=π×()2(x+5) D.π×82x=π×62×5
9.如图6,将一个底面直径为10 cm,高为36 cm的“瘦高”形圆柱锻压(不考虑耗损)成底面直径为20 cm的“矮胖”形圆柱,高变成了多少?
图6
10.一艘驳船的载重量是800吨,容积是795立方米.现在装运生铁和棉花两种货物,每吨生铁的体积是0.3立方米,每吨棉花的体积是4立方米,为了充分利用船的载重量和容积,生铁和棉花各应装多少吨?
命题点 4 根据“表示同一个量的两个不同的式子相等”列方程解决问题
11.将一堆糖果分给幼儿园某班的小朋友,如果每人2颗,那么就多8颗,如果每人3颗,那么就少12颗.这个班有多少名小朋友?
12.某公路一侧原有路灯106盏(两端都有),相邻两盏灯之间的距离为36 m,为节约用电,现计划全部更换为新型节能灯,且相邻两盏灯之间的距离变为54 m,则需要更换新型节能灯多少盏?
13.在一个底面直径为2 cm,高为39 cm的量筒内装满水,再将量筒内的水倒入底面直径为4 cm,高为3 cm的3个烧杯内,能否完全装下?若装不下,量筒内的水还剩多高?
典题讲评与答案详析
1.C [解析] 设长方形的长为x cm,
根据题意,得2(x+15)=72,
解得x=21.
因此,长方形的长为21 cm.
2.B [解析] 小长方形的宽为x cm,则小长方形的长为(14-3x)cm.
根据题意,得6+2x=x+(14-3x).
3.70 [解析] 设剪去的小正方形的边长为x cm.
根据题意,得40×40×x=24000,
解得x=15.
所以原正方形的边长=40+2×15=70(cm).
4.2000 [解析] 设宽为x cm,则其高为=(20-x)cm.
根据题意,得x=20-x,
解得x=10.
故长方体的宽与高均为10 cm,长为40-10×2=20(cm),
所以长方体的体积为20×10×10=2000(cm3).5.[解析] 通过观察可发现6个正方形的边长间存在着数量关系.
将长方形的长用两种不同形式表示,从而建立等量关系.
解:如图,由最小的正方形的面积是1,可知最小的正方形的边长是1.设正方形①的边长为x,则正方形②的边长也为x,正方形③的边长为x+1,正方形④的边长为x+1+1,正方形⑤的边长为x+1+1+1.
根据题意,得x+1+2x=(x+1+1)+(x+1+1+1),解得x=4.
则长方形的长为13,宽为11.
故这个长方形的面积为13×11=143.
6.解:设长方形的宽为x,则长为2x.
根据题意,得2(x+2x)=5+6+13+9,
解得x=5.5.
2×5.5=11.
因此,该长方形的长为11,宽为5.5.
7.解:根据小王的设计可设宽为x米,则长为(x+5)米.根据题意,得2x+(x+5)=35,解得x=10.
因此小王设计的长方形养鸡场的长为10+5=15(米)>14米,故小王的设计不符合实际.
根据小赵的设计可设宽为y米,则长为(y+2)米.
根据题意,得2y+(y+2)=35,解得y=11.
因此小赵设计的长方形养鸡场的长为11+2=13(米)<14米,故小赵的设计符合实际.
按照他的设计,养鸡场的面积为11×13=143(米2).
8.C
9.解:设“矮胖”形圆柱的高变成了x cm.
根据题意,得()2π×36=()2π×x.
解得x=9.
因此,锻压后“矮胖”形圆柱的高变成了9 cm.
10.解:设生铁应装x吨,则棉花应装(800-x)吨.
根据题意,得0.3x+4(800-x)=795.
解得x=650.
800-650=150.
因此,生铁应装650吨,棉花应装150吨.
11.解:设这个班有x名小朋友.
根据题意,得2x+8=3x-12.解得x=20.
因此,这个班有20名小朋友.
12.解:设需要更换新型节能灯x盏.
根据题意,得(106-1)×36=(x-1)×54.
解得x=71.
因此,需要更换新型节能灯71盏.
13.解:V量筒=π×()2×39=39π(cm3),
V烧杯=π×()2×3=12π(cm3),
3×12π=36π(cm3).
因为39π>36π,
所以装不下.
设量筒内的水还剩x cm高.根据题意,得
π×()2×(39-x)=3×π×()2×3.
解得x=3.
即量筒内的水还剩3 cm高.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
