2021-2022学年华东师大版九年级数学上册第23章 图形的相似 单元测试题(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学上册第23章 图形的相似 单元测试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 209.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 23:49:51 | ||
图片预览

文档简介
第23章 图形的相似
一、选择题(每小题4分,共32分)
1.已知=,则下列式子中一定成立的是
( )
A.7x=5y
B.5x=7y
C.x=10y
D.xy=35
2.如图1,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DE=1.2,则DF的长为
( )
图1
A.3.6
B.4.8
C.5
D.5.2
3.在平面直角坐标系中,△OAB各顶点的坐标分别为O(0,0),A(1,2),B(0,3),以点O为位似中心,△OA'B'与△OAB位似,若点B的对应点B'的坐标为(0,-6),则点A的对应点A'的坐标为( )
A.(-2,-4)
B.(-4,-2)
C.(-1,-4)
D.(1,-4)
4.
下列条件中,能判定△ABC与△DEF相似的是
( )
A.
∠A=∠D,=
B.
∠A=∠D,=
C.
∠A=∠D=90°,=
D.
∠A=∠D=90°,∠C=55°,∠F=25°
5.如图2,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则点P'的坐标为
( )
图2
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
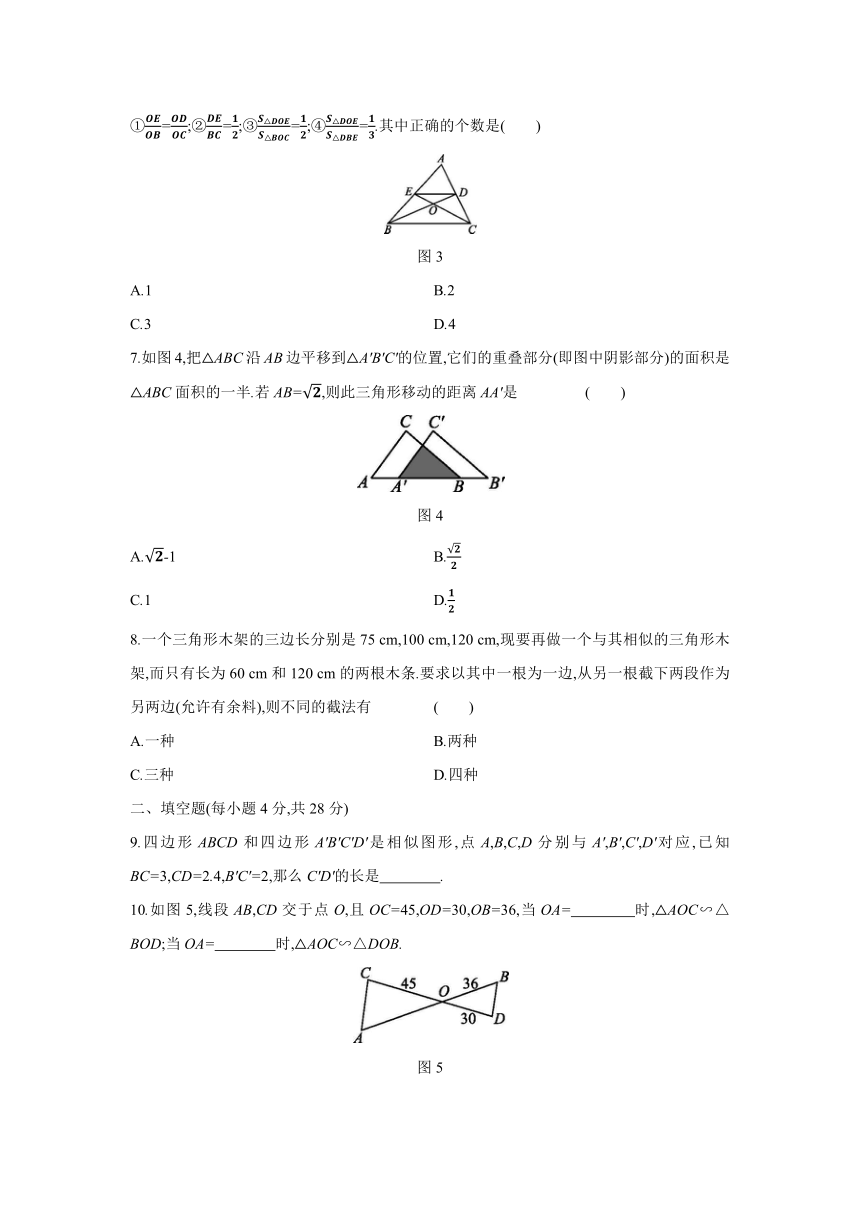
6.如图3,在△ABC中,D,E分别是边AC,AB的中点,BD与CE交于点O,连结DE.有下列结论:①=;②=;③=;④=.其中正确的个数是( )
图3
A.1
B.2
C.3
D.4
7.如图4,把△ABC沿AB边平移到△A'B'C'的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半.若AB=,则此三角形移动的距离AA'是
( )
图4
A.-1
B.
C.1
D.
8.一个三角形木架的三边长分别是75
cm,100
cm,120
cm,现要再做一个与其相似的三角形木架,而只有长为60
cm和120
cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有
( )
A.一种
B.两种
C.三种
D.四种
二、填空题(每小题4分,共28分)
9.四边形ABCD和四边形A'B'C'D'是相似图形,点A,B,C,D分别与A',B',C',D'对应,已知BC=3,CD=2.4,B'C'=2,那么C'D'的长是 .?
10.如图5,线段AB,CD交于点O,且OC=45,OD=30,OB=36,当OA= 时,△AOC∽△BOD;当OA= 时,△AOC∽△DOB.?
图5
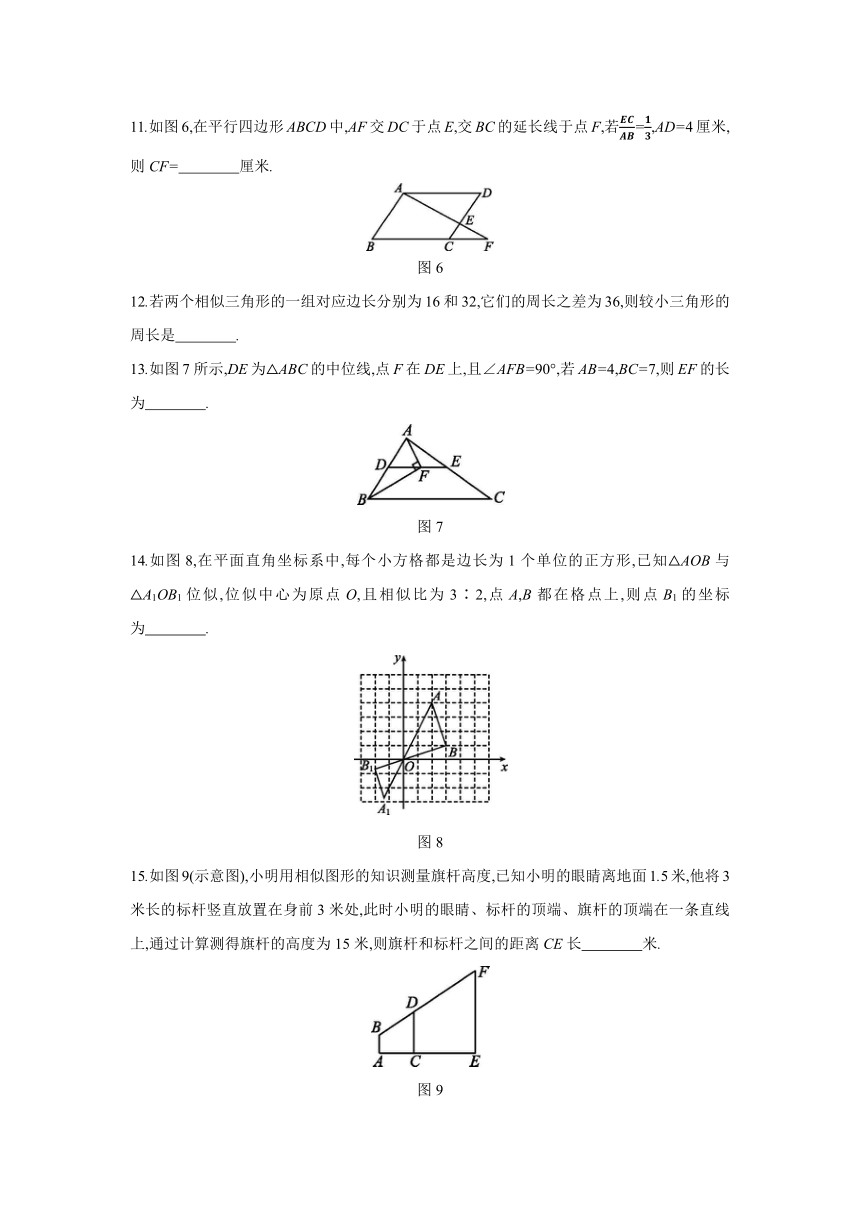
11.如图6,在平行四边形ABCD中,AF交DC于点E,交BC的延长线于点F,若=,AD=4厘米,则CF= 厘米.?
图6
12.若两个相似三角形的一组对应边长分别为16和32,它们的周长之差为36,则较小三角形的周长是 .?
13.如图7所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=7,则EF的长为 .?
图7
14.如图8,在平面直角坐标系中,每个小方格都是边长为1个单位的正方形,已知△AOB与△A1OB1位似,位似中心为原点O,且相似比为3∶2,点A,B都在格点上,则点B1的坐标为 .?
图8
15.如图9(示意图),小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5米,他将3米长的标杆竖直放置在身前3米处,此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算测得旗杆的高度为15米,则旗杆和标杆之间的距离CE长 米.?
图9
三、解答题(共40分)
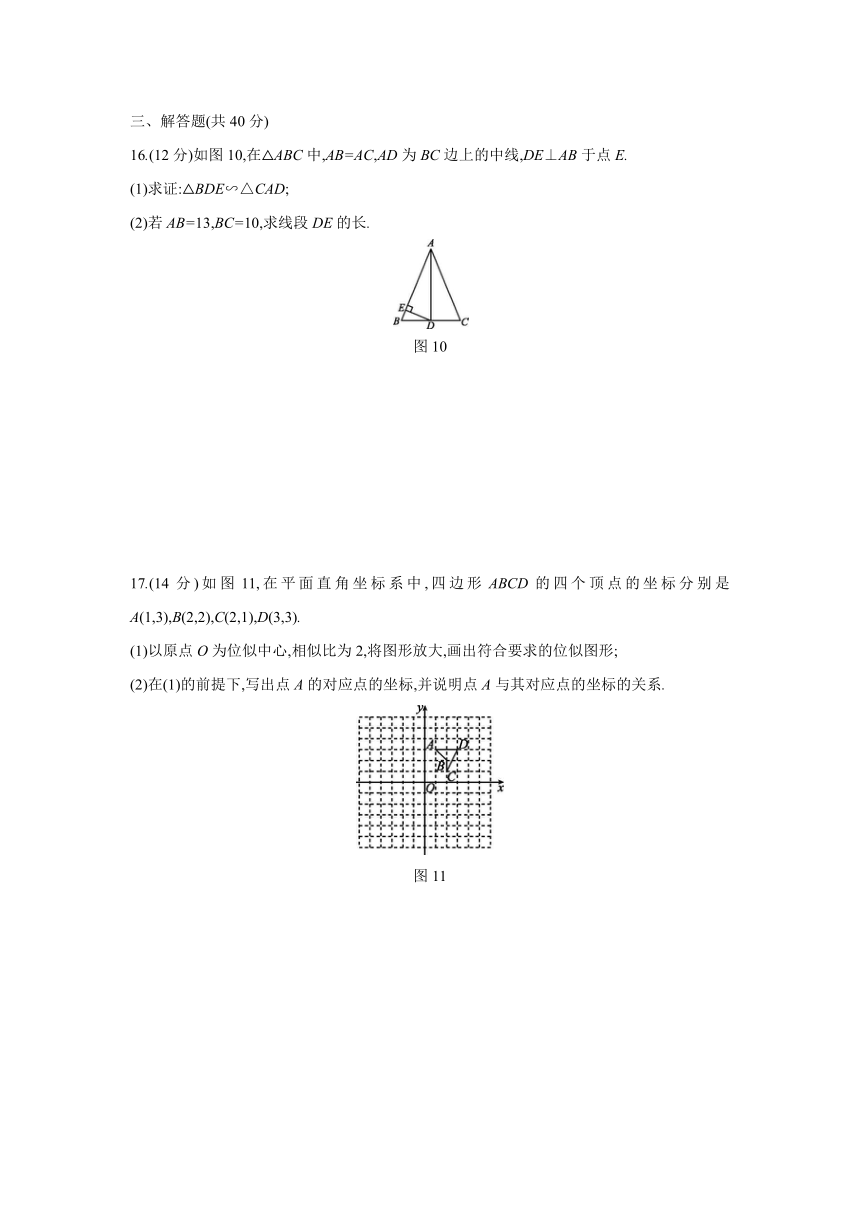
16.(12分)如图10,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
图10
17.(14分)如图11,在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别是A(1,3),B(2,2),C(2,1),D(3,3).
(1)以原点O为位似中心,相似比为2,将图形放大,画出符合要求的位似图形;
(2)在(1)的前提下,写出点A的对应点的坐标,并说明点A与其对应点的坐标的关系.
图11
18.(14分)如图12,在△ABC中,AC=8
cm,BC=16
cm,点P从点A出发,沿着AC边向点C以1
cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2
cm/s的速度运动,如果点P,Q同时出发,那么经过几秒,△PQC和△ABC相似?
图12
答案
1.A
2.B [解析]
∵AD∥BE∥CF,∴=,即=,∴EF=3.6,∴DF=EF+DE=3.6+1.2=4.8.故选B.
3.A [解析]
∵△OA'B'与△OAB关于点O(0,0)成位似图形,且点B(0,3)的对应点B'的坐标为(0,-6),A(1,2),∴A'(-2,-4).故选A.
4.C [解析]
根据两边成比例且夹角相等的两个三角形相似对选项A,B进行判断;
根据勾股定理和两边成比例且夹角相等的两个三角形相似可对选项C进行判断;
根据两角分别相等的两个三角形相似对选项D进行判断.
当∠A=∠D,=时,△ABC∽△DEF,所以A选项错误;
当∠B=∠E,=时,△ABC∽△DEF,所以B选项错误;
当∠A=∠D=90°,=时,△ABC∽△DEF,所以C选项正确;
当∠A=∠D=90°,∠C=55°,∠F=35°时,可判定△ABC与△DEF相似,所以D选项错误.故选C.
5.D [解析]
过点P作PQ⊥y轴于点Q,
如图.∵P(2,3),
∴PQ=2,OQ=3.
∵点P(2,3)绕原点O顺时针旋转90°得到点P',相当于把△OPQ绕原点O顺时针旋转90°得到△OP'Q',
∴∠P'Q'O=90°,∠QOQ'=90°,P'Q'=PQ=2,OQ'=OQ=3,∴点P'的坐标为(3,-2).故选D.
6.B [解析]
∵D,E分别是边AC,AB的中点,∴DE是△ABC的中位线,∴DE∥BC且=,②正确;∴∠ODE=∠OBC,∠OED=∠OCB,∴△ODE∽△OBC,∴===,①错误;=()2=,③错误;设△BDE中BD边上的高为h.∵===,∴=,④正确.故选B.
7.A
8.B [解析]
长120
cm的木条与三角形木架的最长边相等,要满足两边之和大于第三边,则长120
cm的木条不能作为一边,
设从120
cm的木条上截下两段长分别为x
cm,y
cm(x由于长60
cm的木条不能与75
cm的一边对应,否则x+y>120
cm.
若长60
cm的木条与100
cm的一边对应,则==,
解得x=45,y=72.
x+y=45+72=117<120,符合题意;
若长60
cm的木条与120
cm的一边对应,则==,
解得x=37.5,y=50.
x+y=37.5+50=87.5<120,符合题意.
所以有两种不同的截法:把120
cm的木条截成45
cm,72
cm两段或把120
cm的木条截成37.5
cm,50
cm两段.故选B.
9.1.6
10.54 37.5 [解析]
当△AOC∽△BOD时,=,∴=,∴OA=54;
当△AOC∽△DOB时,=,
∴=,∴OA=37.5.
11.2
12.36 [解析]
周长比=相似比.
13.1.5 [解析]
∵DE为△ABC的中位线,
∴DE=BC=3.5.
在Rt△AFB中,∠AFB=90°,D是斜边AB的中点,
∴DF=AB=2,
∴EF=DE-DF=1.5.
14.(-2,-) [解析]
由题意,得△AOB与△A1OB1位似,位似中心为原点O,且相似比为3∶2.又∵B(3,1),∴点B1的坐标是[3×(-),1×(-)],即点B1的坐标是(-2,-).故答案为(-2,-).
15.24 [解析]
如图,延长FB交EA的延长线于点T.设TA=x米,CE=y米.
由题意,得AB=1.5米,AC=CD=3米,EF=15米
∵AB∥CD,∴△TAB∽△TCD,
∴=,
∴=,解得x=3.
经检验,x=3是原分式方程的解.
∵CD∥EF,
∴△TCD∽△TEF,∴=,
∴=,解得y=24.
经检验,y=24是原分式方程的解.
∴CE=24(米).
16.解:(1)证明:∵AD为BC边上的中线,AB=AC,∴AD⊥BC,∠B=∠C.
∵DE⊥AB,∴∠DEB=∠ADC=90°,
∴△BDE∽△CAD.
(2)∵BD=CD,BC=10,∴BD=5.
在Rt△ADB中,AD===12.
∵AD·BD=AB·DE,∴DE=.
17.解:(1)符合要求的位似图形有两个:四边形A'B'C'D'和四边形A″B″C″D″,如图所示.
(2)点A的对应点有2个,分别是A'(2,6),A″(-2,-6).
关系:点A的对应点的横、纵坐标分别是点A的横、纵坐标分别乘以2或-2.
18.解:设经过x
s,△PQC和△ABC相似.
则CP=AC-AP=(8-x)cm,CQ=2x
cm.
①当CP与AC是对应边时,=,
即=,解得x=4;
②当CP与BC是对应边时,=,
即=,解得x=.
故经过4
s或
s,△PQC和△ABC相似.
一、选择题(每小题4分,共32分)
1.已知=,则下列式子中一定成立的是
( )
A.7x=5y
B.5x=7y
C.x=10y
D.xy=35
2.如图1,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DE=1.2,则DF的长为
( )
图1
A.3.6
B.4.8
C.5
D.5.2
3.在平面直角坐标系中,△OAB各顶点的坐标分别为O(0,0),A(1,2),B(0,3),以点O为位似中心,△OA'B'与△OAB位似,若点B的对应点B'的坐标为(0,-6),则点A的对应点A'的坐标为( )
A.(-2,-4)
B.(-4,-2)
C.(-1,-4)
D.(1,-4)
4.
下列条件中,能判定△ABC与△DEF相似的是
( )
A.
∠A=∠D,=
B.
∠A=∠D,=
C.
∠A=∠D=90°,=
D.
∠A=∠D=90°,∠C=55°,∠F=25°
5.如图2,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则点P'的坐标为
( )
图2
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
6.如图3,在△ABC中,D,E分别是边AC,AB的中点,BD与CE交于点O,连结DE.有下列结论:①=;②=;③=;④=.其中正确的个数是( )
图3
A.1
B.2
C.3
D.4
7.如图4,把△ABC沿AB边平移到△A'B'C'的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半.若AB=,则此三角形移动的距离AA'是
( )
图4
A.-1
B.
C.1
D.
8.一个三角形木架的三边长分别是75
cm,100
cm,120
cm,现要再做一个与其相似的三角形木架,而只有长为60
cm和120
cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有
( )
A.一种
B.两种
C.三种
D.四种
二、填空题(每小题4分,共28分)
9.四边形ABCD和四边形A'B'C'D'是相似图形,点A,B,C,D分别与A',B',C',D'对应,已知BC=3,CD=2.4,B'C'=2,那么C'D'的长是 .?
10.如图5,线段AB,CD交于点O,且OC=45,OD=30,OB=36,当OA= 时,△AOC∽△BOD;当OA= 时,△AOC∽△DOB.?
图5
11.如图6,在平行四边形ABCD中,AF交DC于点E,交BC的延长线于点F,若=,AD=4厘米,则CF= 厘米.?
图6
12.若两个相似三角形的一组对应边长分别为16和32,它们的周长之差为36,则较小三角形的周长是 .?
13.如图7所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=7,则EF的长为 .?
图7
14.如图8,在平面直角坐标系中,每个小方格都是边长为1个单位的正方形,已知△AOB与△A1OB1位似,位似中心为原点O,且相似比为3∶2,点A,B都在格点上,则点B1的坐标为 .?
图8
15.如图9(示意图),小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5米,他将3米长的标杆竖直放置在身前3米处,此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算测得旗杆的高度为15米,则旗杆和标杆之间的距离CE长 米.?
图9
三、解答题(共40分)
16.(12分)如图10,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
图10
17.(14分)如图11,在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别是A(1,3),B(2,2),C(2,1),D(3,3).
(1)以原点O为位似中心,相似比为2,将图形放大,画出符合要求的位似图形;
(2)在(1)的前提下,写出点A的对应点的坐标,并说明点A与其对应点的坐标的关系.
图11
18.(14分)如图12,在△ABC中,AC=8
cm,BC=16
cm,点P从点A出发,沿着AC边向点C以1
cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2
cm/s的速度运动,如果点P,Q同时出发,那么经过几秒,△PQC和△ABC相似?
图12
答案
1.A
2.B [解析]
∵AD∥BE∥CF,∴=,即=,∴EF=3.6,∴DF=EF+DE=3.6+1.2=4.8.故选B.
3.A [解析]
∵△OA'B'与△OAB关于点O(0,0)成位似图形,且点B(0,3)的对应点B'的坐标为(0,-6),A(1,2),∴A'(-2,-4).故选A.
4.C [解析]
根据两边成比例且夹角相等的两个三角形相似对选项A,B进行判断;
根据勾股定理和两边成比例且夹角相等的两个三角形相似可对选项C进行判断;
根据两角分别相等的两个三角形相似对选项D进行判断.
当∠A=∠D,=时,△ABC∽△DEF,所以A选项错误;
当∠B=∠E,=时,△ABC∽△DEF,所以B选项错误;
当∠A=∠D=90°,=时,△ABC∽△DEF,所以C选项正确;
当∠A=∠D=90°,∠C=55°,∠F=35°时,可判定△ABC与△DEF相似,所以D选项错误.故选C.
5.D [解析]
过点P作PQ⊥y轴于点Q,
如图.∵P(2,3),
∴PQ=2,OQ=3.
∵点P(2,3)绕原点O顺时针旋转90°得到点P',相当于把△OPQ绕原点O顺时针旋转90°得到△OP'Q',
∴∠P'Q'O=90°,∠QOQ'=90°,P'Q'=PQ=2,OQ'=OQ=3,∴点P'的坐标为(3,-2).故选D.
6.B [解析]
∵D,E分别是边AC,AB的中点,∴DE是△ABC的中位线,∴DE∥BC且=,②正确;∴∠ODE=∠OBC,∠OED=∠OCB,∴△ODE∽△OBC,∴===,①错误;=()2=,③错误;设△BDE中BD边上的高为h.∵===,∴=,④正确.故选B.
7.A
8.B [解析]
长120
cm的木条与三角形木架的最长边相等,要满足两边之和大于第三边,则长120
cm的木条不能作为一边,
设从120
cm的木条上截下两段长分别为x
cm,y
cm(x
cm的木条不能与75
cm的一边对应,否则x+y>120
cm.
若长60
cm的木条与100
cm的一边对应,则==,
解得x=45,y=72.
x+y=45+72=117<120,符合题意;
若长60
cm的木条与120
cm的一边对应,则==,
解得x=37.5,y=50.
x+y=37.5+50=87.5<120,符合题意.
所以有两种不同的截法:把120
cm的木条截成45
cm,72
cm两段或把120
cm的木条截成37.5
cm,50
cm两段.故选B.
9.1.6
10.54 37.5 [解析]
当△AOC∽△BOD时,=,∴=,∴OA=54;
当△AOC∽△DOB时,=,
∴=,∴OA=37.5.
11.2
12.36 [解析]
周长比=相似比.
13.1.5 [解析]
∵DE为△ABC的中位线,
∴DE=BC=3.5.
在Rt△AFB中,∠AFB=90°,D是斜边AB的中点,
∴DF=AB=2,
∴EF=DE-DF=1.5.
14.(-2,-) [解析]
由题意,得△AOB与△A1OB1位似,位似中心为原点O,且相似比为3∶2.又∵B(3,1),∴点B1的坐标是[3×(-),1×(-)],即点B1的坐标是(-2,-).故答案为(-2,-).
15.24 [解析]
如图,延长FB交EA的延长线于点T.设TA=x米,CE=y米.
由题意,得AB=1.5米,AC=CD=3米,EF=15米
∵AB∥CD,∴△TAB∽△TCD,
∴=,
∴=,解得x=3.
经检验,x=3是原分式方程的解.
∵CD∥EF,
∴△TCD∽△TEF,∴=,
∴=,解得y=24.
经检验,y=24是原分式方程的解.
∴CE=24(米).
16.解:(1)证明:∵AD为BC边上的中线,AB=AC,∴AD⊥BC,∠B=∠C.
∵DE⊥AB,∴∠DEB=∠ADC=90°,
∴△BDE∽△CAD.
(2)∵BD=CD,BC=10,∴BD=5.
在Rt△ADB中,AD===12.
∵AD·BD=AB·DE,∴DE=.
17.解:(1)符合要求的位似图形有两个:四边形A'B'C'D'和四边形A″B″C″D″,如图所示.
(2)点A的对应点有2个,分别是A'(2,6),A″(-2,-6).
关系:点A的对应点的横、纵坐标分别是点A的横、纵坐标分别乘以2或-2.
18.解:设经过x
s,△PQC和△ABC相似.
则CP=AC-AP=(8-x)cm,CQ=2x
cm.
①当CP与AC是对应边时,=,
即=,解得x=4;
②当CP与BC是对应边时,=,
即=,解得x=.
故经过4
s或
s,△PQC和△ABC相似.
