《1.3勾股定理的应用》同步专题突破训练(附答案) 2021-2022学年八年级数学北师大版上册
文档属性
| 名称 | 《1.3勾股定理的应用》同步专题突破训练(附答案) 2021-2022学年八年级数学北师大版上册 |  | |
| 格式 | doc | ||
| 文件大小 | 280.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 13:16:02 | ||
图片预览



文档简介
2021年北师大版八年级数学上册《1.3勾股定理的应用》同步专题突破训练(附答案)
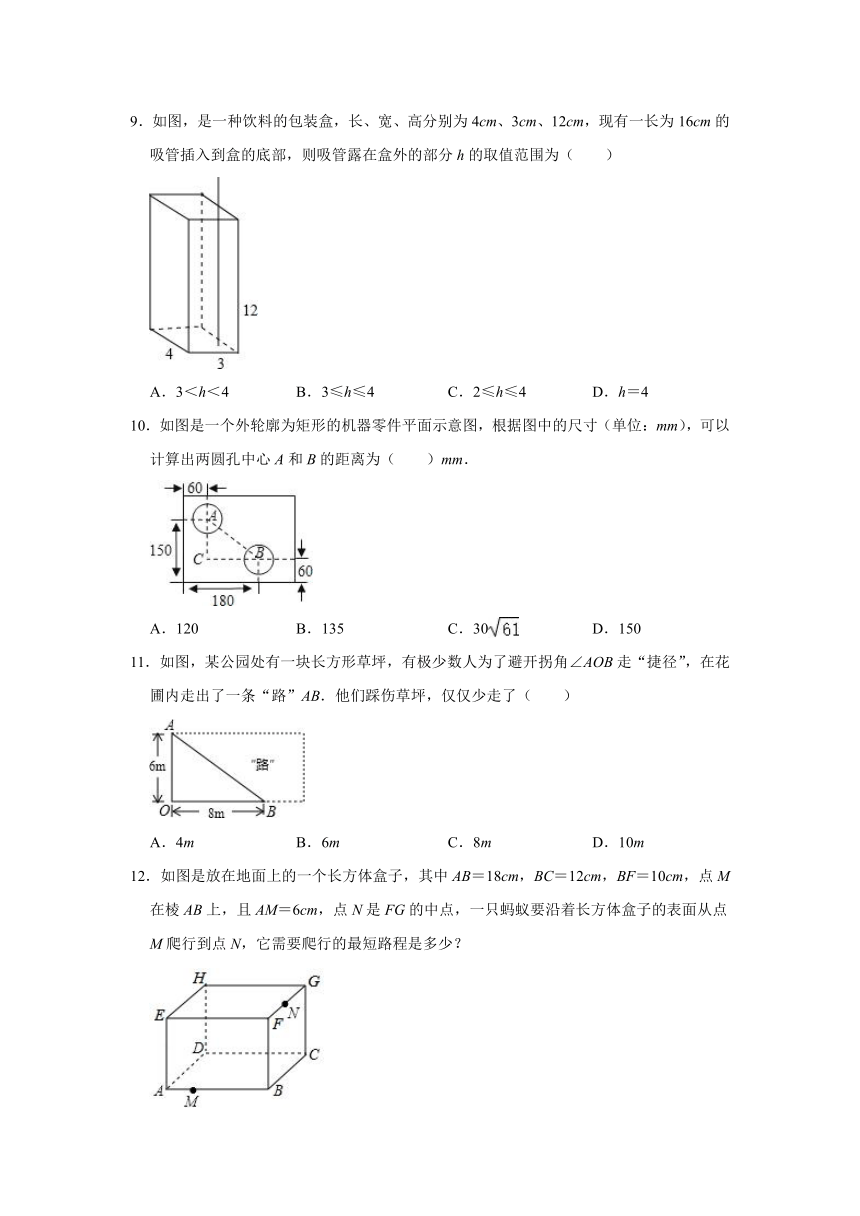
1.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )
A.8cm B.10cm C.12cm D.15cm
2.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周四尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”,题意是:如图所示,把枯木看成一个圆柱体,因一丈为十尺,则圆柱体高为20尺,底面周长四尺,有葛藤自A点缠绕而上,绕5周后其末端恰好到达点B处,则问题中葛藤的最短长度是( )尺.
A.25 B.20 C.4 D.2
3.如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )
A.10 B.50 C.120 D.130
4.如图,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S,若BC=8,点P移动的最短距离为5,则圆柱的底面周长为( )
A.6 B.4π C.8 D.10
5.如图,圆柱形玻璃杯高为11cm,底面周长为30cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的爬行最短路线长为(杯壁厚度不计)( )
A.12cm B.17cm C.20cm D.25cm
6.如图在实践活动课上,小华打算测量学校旗杆的高度,她发现旗杆顶端的绳子垂到地面后还多出1m,当她把绳子斜拉直,且使绳子的底端刚好接触地面时,测得绳子底端距离旗杆底部5m,由此可计算出学校旗杆的高度是( )
A.8m B.10m C.12m D.15m
7.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要( )
A.17m B.18m C.25m D.26m
8.一个门框的尺寸如图所示,下列长×宽型号(单位:m)的长方形薄木板能从门框中通过的是( )
A.2.9×2.2 B.2.8×2.3 C.2.7×2.4 D.2.6×2.5
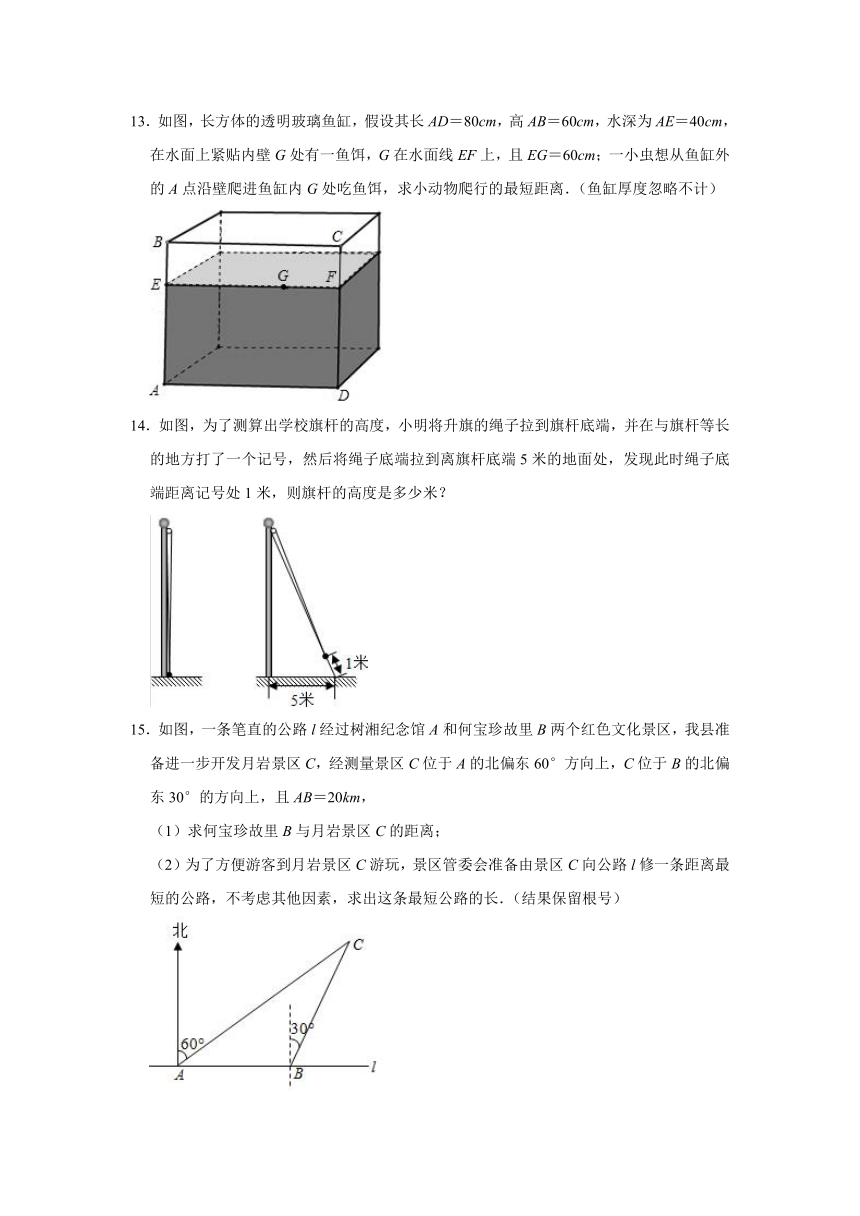
9.如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为( )
A.3<h<4 B.3≤h≤4 C.2≤h≤4 D.h=4
10.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),可以计算出两圆孔中心A和B的距离为( )mm.
A.120 B.135 C.30 D.150
11.如图,某公园处有一块长方形草坪,有极少数人为了避开拐角∠AOB走“捷径”,在花圃内走出了一条“路”AB.他们踩伤草坪,仅仅少走了( )
A.4m B.6m C.8m D.10m
12.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程是多少?
13.如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,求小动物爬行的最短距离.(鱼缸厚度忽略不计)
14.如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个记号,然后将绳子底端拉到离旗杆底端5米的地面处,发现此时绳子底端距离记号处1米,则旗杆的高度是多少米?
15.如图,一条笔直的公路l经过树湘纪念馆A和何宝珍故里B两个红色文化景区,我县准备进一步开发月岩景区C,经测量景区C位于A的北偏东60°方向上,C位于B的北偏东30°的方向上,且AB=20km,
(1)求何宝珍故里B与月岩景区C的距离;
(2)为了方便游客到月岩景区C游玩,景区管委会准备由景区C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
16.如图,一架梯子AB斜靠在一竖直的墙OA上,这时AO=2.5m,∠OAB=30°.梯子顶端A沿墙下滑至点C,使∠OCD=60°,同时,梯子底端B也外移至点D.求BD的长度.(结果保留根号)
17.某运动公园有一块空地,如图,△ABC所示,∠ACB=90°,公园管理处计划在△ADC区域内安装健身器材,其余部分种植草坪,绿化环境.经测量:CD=30米,AD=40米,BC=120米,AB=130米.
(1)求证:∠ADC=90°;
(2)若种植草坪的费用每平方米300元,求种植草坪的总费用.
有一个水池,截面是一个边长为12尺的正方形,在水池正中央有一根新生的芦苇,它高出水面2尺,如图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?
19.学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?
20.如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
21.已知某学校有一块三角形空地ABC,如图所示,现计划在空地上种植草皮,经测量,BD=6m,BC=10m,CD=8m,AC=17m,若每平方米草皮需要200元,求一共需要投入多少元.
22.如图,在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=2千米,CH=1.6千米,HB=1.2千米
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明.
(2)求原来的路线AC的长.
参考答案
1.解:将三棱柱沿AA′展开,其展开图如图,
则AA′==15(cm).
故选:D.
2.解:如图,一条直角边(即枯木的高)长20尺,
另一条直角边长5×4=20(尺),
因此葛藤长为=20(尺).
故选:B.
3.解:如图所示,
∵它的每一级的长宽高为20cm,宽30cm,长50cm,
∴AB==50(cm).
答:蚂蚁沿着台阶面爬行到点B的最短路程是50cm,
故选:B.
4.解:如图所示,
在圆柱的截面ABCD中,BC=8,
设AB=x,
∵点P移动的最短距离为5,
∴AS=5,
∵点S是BC的中点,
∴BS=BC=4,
∴AB==3,
∴圆柱的底面周长为2AB=6.
故选:A.
5.解:如图:
将杯子侧面展开,
作A关于EF的对称点A′,
则AF+BF为蚂蚁从外壁A处到内壁B处的最短距离,即A′B的长度,
∵A′B====17(cm),
∴蚂蚁从外壁A处到内壁B处的最短距离为17cm,
故选:B.
6.解:设旗杆的高度为x米,则绳子的长度为(x+1)米,
根据勾股定理可得:x2+52=(x+1)2,
解得,x=12.
即旗杆的高度为12米.
故选:C.
7.解:由勾股定理得:
楼梯的水平宽度==12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是12+5=17(米).
故选:A.
8.解:薄木板不能从门框内通过.理由如下:
连接AC,则AC与AB、BC构成直角三角形,
根据勾股定理得AC===≈2.236>2.2.
∴只有2.9×2.2薄木板能从门框内通过,
故选:A.
9.解:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16﹣12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线直径为5cm,高为12cm,
由勾股定理可得杯里面管长为=13cm,则露在杯口外的长度最长为16﹣13=3cm;
则可得露在杯口外的长度在3cm和4cm范围变化.
故选:B.
10.解:如图,在Rt△ABC中,∵AC=150﹣60=90,BC=180﹣60=120,
∴AB==150(mm),
∴两圆孔中心A和B的距离为150mm.
故选:D.
11.解:在Rt△AOB中,AB==10m,
∴AO+BO﹣AB=6+8﹣10=4m.
即少走了4m.
故选:A.
12.解:如图1,
∵AB=18cm,BC=GF=12cm,BF=10cm,
∴BM=18﹣6=12,BN=10+6=16,
∴MN==20(cm);
如图2,
∵AB=18cm,BC=GF=12cm,BF=10cm,
∴PM=18﹣6+6=18,NP=10,
∴MN==2(cm).
∴蚂蚁沿长方体表面爬到米粒处的最短距离为20cm.
13.解:如图所示作点A关于BC的对称点A′,连接A′G交BC与点Q,小虫沿着A→Q→G的路线爬行时路程最短.
在直角△A′EG中,A′E=80cm,EG=60cm,
∴AQ+QG=A′Q+QG=A′G==100cm.
∴最短路线长为100cm.
14.解:如图,设旗杆的高度为xm,则AC=xm,AB=(x+1)m,BC=5m,
在Rt△ABC中,52+x2=(x+1)2,
解得x=12,
答:旗杆的高度是12m.
15.解:(1)根据题意得:∠CAB=30°,∠ABC=120°,
∴∠ACB=180°﹣∠CAB﹣∠ABC=180°﹣30°﹣120°=30°,
∴∠CAB=∠ACB,
∴BC=AB=20(km).
答:何宝珍故里B到月岩景区C的距离为20km;
(2)过点C作CD⊥l,垂足为D,则CD的长是这条最短公路的长.
∵CD⊥l,
∴∠CDB=90°,
∵∠CBD=180°﹣∠ABC=180°﹣120°=60°,
∴∠BCD=180°﹣∠CBD﹣∠CDB=180°﹣60°﹣90°=30°,
在Rt△BCD中,∠CDB=90°,∠BCD=30°,BC=20km,
∴,
(km).
答:这条最短公路的长为km.
16.解:在Rt△ABO中,∵AO=2.5,∠OAB=30°,
∴AB=,
根据勾股定理知BO===,
∵∠OCD=60°,
∴∠ODC=30°,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS),
∴OA=OD,OC=OB,
∴BD=OD﹣OB=﹣=.
17.(1)证明:∵∠ACB=90°,
∴△ACB是直角三角形,
∵BC=120米,AB=130米,
∴AC===50(米),
∵CD=30米,AD=40米,
∴CD2+AD2=AC2,
∴△ADC是直角三角形,
∴∠ADC=90°;
(2)由(1)得:种植草坪的面积为:
×AC×BC﹣×AD×DC=×50×120﹣×30×40=2400(平方米),
∵种植草坪的费用每平方米300元,
∴2400×300=720000(元),
答:种植草坪的总费用为720000元.
18.解:设水深为x尺,则芦苇长为(x+2)尺,
根据勾股定理得:x2+()2=(x+2)2,
解得:x=8,
芦苇的长度=8+2=10(尺),
答:水池深8尺,芦苇长10尺.
19.解:过点A作AD⊥BC于点D,设BD=x,则CD=14﹣x,
在Rt△ABD与Rt△ACD中,
∵AD2=AB2﹣BD2,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,即132﹣x2=152﹣(14﹣x)2,解得x=5,
∴AD2=AB2﹣BD2=132﹣52=144,
∴AD=12(米),
∴学校修建这个花园的费用=30××14×12=2520(元).
答:学校修建这个花园需要投资2520元.
20.解:∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设AE=x,则BE=AB﹣AE=(25﹣x),
∵DA=15km,CB=10km,
∴x2+152=(25﹣x)2+102,
解得:x=10,
∴AE=10km,
∴收购站E应建在离A点10km处.
21.解:在△CBD 中,
∵BD=6m,BC=10m,CD=8m,
∴BD2+CD2=62+82=102=BC2,
∴△CBD 是直角三角形,
∴∠CDB=90°,
∴∠CDA=90°,
在Rt△ADC中,AD=(m),
∴S△ADC=AD?CD=×15×8=60(m2),
∴S△CBD=DB?CD=×6×8=24(m)2,
∴三角形ABC的面积是84m2,
∵每平方米草皮需要 200元,
∴总投入=84×200=16800( 元).
22.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(1.6)2+(1.2)2=4,
BC2=4,
∴CH2+BH2=BC2,
∴CH⊥AB,
所以CH是从村庄C到河边的最近路;
(2)设AC=x千米,
在Rt△ACH中,由已知得AC=x,AH=x﹣1.2,CH=1.6,
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣1.2)2+(1.6)2,
解这个方程,得x=,
答:原来的路线AC的长为千米.
1.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )
A.8cm B.10cm C.12cm D.15cm
2.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周四尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”,题意是:如图所示,把枯木看成一个圆柱体,因一丈为十尺,则圆柱体高为20尺,底面周长四尺,有葛藤自A点缠绕而上,绕5周后其末端恰好到达点B处,则问题中葛藤的最短长度是( )尺.
A.25 B.20 C.4 D.2
3.如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )
A.10 B.50 C.120 D.130
4.如图,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S,若BC=8,点P移动的最短距离为5,则圆柱的底面周长为( )
A.6 B.4π C.8 D.10
5.如图,圆柱形玻璃杯高为11cm,底面周长为30cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的爬行最短路线长为(杯壁厚度不计)( )
A.12cm B.17cm C.20cm D.25cm
6.如图在实践活动课上,小华打算测量学校旗杆的高度,她发现旗杆顶端的绳子垂到地面后还多出1m,当她把绳子斜拉直,且使绳子的底端刚好接触地面时,测得绳子底端距离旗杆底部5m,由此可计算出学校旗杆的高度是( )
A.8m B.10m C.12m D.15m
7.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要( )
A.17m B.18m C.25m D.26m
8.一个门框的尺寸如图所示,下列长×宽型号(单位:m)的长方形薄木板能从门框中通过的是( )
A.2.9×2.2 B.2.8×2.3 C.2.7×2.4 D.2.6×2.5
9.如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为( )
A.3<h<4 B.3≤h≤4 C.2≤h≤4 D.h=4
10.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),可以计算出两圆孔中心A和B的距离为( )mm.
A.120 B.135 C.30 D.150
11.如图,某公园处有一块长方形草坪,有极少数人为了避开拐角∠AOB走“捷径”,在花圃内走出了一条“路”AB.他们踩伤草坪,仅仅少走了( )
A.4m B.6m C.8m D.10m
12.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程是多少?
13.如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,求小动物爬行的最短距离.(鱼缸厚度忽略不计)
14.如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个记号,然后将绳子底端拉到离旗杆底端5米的地面处,发现此时绳子底端距离记号处1米,则旗杆的高度是多少米?
15.如图,一条笔直的公路l经过树湘纪念馆A和何宝珍故里B两个红色文化景区,我县准备进一步开发月岩景区C,经测量景区C位于A的北偏东60°方向上,C位于B的北偏东30°的方向上,且AB=20km,
(1)求何宝珍故里B与月岩景区C的距离;
(2)为了方便游客到月岩景区C游玩,景区管委会准备由景区C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
16.如图,一架梯子AB斜靠在一竖直的墙OA上,这时AO=2.5m,∠OAB=30°.梯子顶端A沿墙下滑至点C,使∠OCD=60°,同时,梯子底端B也外移至点D.求BD的长度.(结果保留根号)
17.某运动公园有一块空地,如图,△ABC所示,∠ACB=90°,公园管理处计划在△ADC区域内安装健身器材,其余部分种植草坪,绿化环境.经测量:CD=30米,AD=40米,BC=120米,AB=130米.
(1)求证:∠ADC=90°;
(2)若种植草坪的费用每平方米300元,求种植草坪的总费用.
有一个水池,截面是一个边长为12尺的正方形,在水池正中央有一根新生的芦苇,它高出水面2尺,如图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?
19.学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?
20.如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
21.已知某学校有一块三角形空地ABC,如图所示,现计划在空地上种植草皮,经测量,BD=6m,BC=10m,CD=8m,AC=17m,若每平方米草皮需要200元,求一共需要投入多少元.
22.如图,在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=2千米,CH=1.6千米,HB=1.2千米
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明.
(2)求原来的路线AC的长.
参考答案
1.解:将三棱柱沿AA′展开,其展开图如图,
则AA′==15(cm).
故选:D.
2.解:如图,一条直角边(即枯木的高)长20尺,
另一条直角边长5×4=20(尺),
因此葛藤长为=20(尺).
故选:B.
3.解:如图所示,
∵它的每一级的长宽高为20cm,宽30cm,长50cm,
∴AB==50(cm).
答:蚂蚁沿着台阶面爬行到点B的最短路程是50cm,
故选:B.
4.解:如图所示,
在圆柱的截面ABCD中,BC=8,
设AB=x,
∵点P移动的最短距离为5,
∴AS=5,
∵点S是BC的中点,
∴BS=BC=4,
∴AB==3,
∴圆柱的底面周长为2AB=6.
故选:A.
5.解:如图:
将杯子侧面展开,
作A关于EF的对称点A′,
则AF+BF为蚂蚁从外壁A处到内壁B处的最短距离,即A′B的长度,
∵A′B====17(cm),
∴蚂蚁从外壁A处到内壁B处的最短距离为17cm,
故选:B.
6.解:设旗杆的高度为x米,则绳子的长度为(x+1)米,
根据勾股定理可得:x2+52=(x+1)2,
解得,x=12.
即旗杆的高度为12米.
故选:C.
7.解:由勾股定理得:
楼梯的水平宽度==12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是12+5=17(米).
故选:A.
8.解:薄木板不能从门框内通过.理由如下:
连接AC,则AC与AB、BC构成直角三角形,
根据勾股定理得AC===≈2.236>2.2.
∴只有2.9×2.2薄木板能从门框内通过,
故选:A.
9.解:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16﹣12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线直径为5cm,高为12cm,
由勾股定理可得杯里面管长为=13cm,则露在杯口外的长度最长为16﹣13=3cm;
则可得露在杯口外的长度在3cm和4cm范围变化.
故选:B.
10.解:如图,在Rt△ABC中,∵AC=150﹣60=90,BC=180﹣60=120,
∴AB==150(mm),
∴两圆孔中心A和B的距离为150mm.
故选:D.
11.解:在Rt△AOB中,AB==10m,
∴AO+BO﹣AB=6+8﹣10=4m.
即少走了4m.
故选:A.
12.解:如图1,
∵AB=18cm,BC=GF=12cm,BF=10cm,
∴BM=18﹣6=12,BN=10+6=16,
∴MN==20(cm);
如图2,
∵AB=18cm,BC=GF=12cm,BF=10cm,
∴PM=18﹣6+6=18,NP=10,
∴MN==2(cm).
∴蚂蚁沿长方体表面爬到米粒处的最短距离为20cm.
13.解:如图所示作点A关于BC的对称点A′,连接A′G交BC与点Q,小虫沿着A→Q→G的路线爬行时路程最短.
在直角△A′EG中,A′E=80cm,EG=60cm,
∴AQ+QG=A′Q+QG=A′G==100cm.
∴最短路线长为100cm.
14.解:如图,设旗杆的高度为xm,则AC=xm,AB=(x+1)m,BC=5m,
在Rt△ABC中,52+x2=(x+1)2,
解得x=12,
答:旗杆的高度是12m.
15.解:(1)根据题意得:∠CAB=30°,∠ABC=120°,
∴∠ACB=180°﹣∠CAB﹣∠ABC=180°﹣30°﹣120°=30°,
∴∠CAB=∠ACB,
∴BC=AB=20(km).
答:何宝珍故里B到月岩景区C的距离为20km;
(2)过点C作CD⊥l,垂足为D,则CD的长是这条最短公路的长.
∵CD⊥l,
∴∠CDB=90°,
∵∠CBD=180°﹣∠ABC=180°﹣120°=60°,
∴∠BCD=180°﹣∠CBD﹣∠CDB=180°﹣60°﹣90°=30°,
在Rt△BCD中,∠CDB=90°,∠BCD=30°,BC=20km,
∴,
(km).
答:这条最短公路的长为km.
16.解:在Rt△ABO中,∵AO=2.5,∠OAB=30°,
∴AB=,
根据勾股定理知BO===,
∵∠OCD=60°,
∴∠ODC=30°,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS),
∴OA=OD,OC=OB,
∴BD=OD﹣OB=﹣=.
17.(1)证明:∵∠ACB=90°,
∴△ACB是直角三角形,
∵BC=120米,AB=130米,
∴AC===50(米),
∵CD=30米,AD=40米,
∴CD2+AD2=AC2,
∴△ADC是直角三角形,
∴∠ADC=90°;
(2)由(1)得:种植草坪的面积为:
×AC×BC﹣×AD×DC=×50×120﹣×30×40=2400(平方米),
∵种植草坪的费用每平方米300元,
∴2400×300=720000(元),
答:种植草坪的总费用为720000元.
18.解:设水深为x尺,则芦苇长为(x+2)尺,
根据勾股定理得:x2+()2=(x+2)2,
解得:x=8,
芦苇的长度=8+2=10(尺),
答:水池深8尺,芦苇长10尺.
19.解:过点A作AD⊥BC于点D,设BD=x,则CD=14﹣x,
在Rt△ABD与Rt△ACD中,
∵AD2=AB2﹣BD2,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,即132﹣x2=152﹣(14﹣x)2,解得x=5,
∴AD2=AB2﹣BD2=132﹣52=144,
∴AD=12(米),
∴学校修建这个花园的费用=30××14×12=2520(元).
答:学校修建这个花园需要投资2520元.
20.解:∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设AE=x,则BE=AB﹣AE=(25﹣x),
∵DA=15km,CB=10km,
∴x2+152=(25﹣x)2+102,
解得:x=10,
∴AE=10km,
∴收购站E应建在离A点10km处.
21.解:在△CBD 中,
∵BD=6m,BC=10m,CD=8m,
∴BD2+CD2=62+82=102=BC2,
∴△CBD 是直角三角形,
∴∠CDB=90°,
∴∠CDA=90°,
在Rt△ADC中,AD=(m),
∴S△ADC=AD?CD=×15×8=60(m2),
∴S△CBD=DB?CD=×6×8=24(m)2,
∴三角形ABC的面积是84m2,
∵每平方米草皮需要 200元,
∴总投入=84×200=16800( 元).
22.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(1.6)2+(1.2)2=4,
BC2=4,
∴CH2+BH2=BC2,
∴CH⊥AB,
所以CH是从村庄C到河边的最近路;
(2)设AC=x千米,
在Rt△ACH中,由已知得AC=x,AH=x﹣1.2,CH=1.6,
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣1.2)2+(1.6)2,
解这个方程,得x=,
答:原来的路线AC的长为千米.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
