2021——2022学年京改版七年级数学上册第三章 简单的几何图形 单元测试题(word版含答案)
文档属性
| 名称 | 2021——2022学年京改版七年级数学上册第三章 简单的几何图形 单元测试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 139.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览



文档简介
第三章 简单的几何图形
一、选择题(本大题共6小题,每小题4分,共24分)
1.下列几何体中,同一个几何体从上面看和从正面看得到的图形不同的是
( )
图1
2.一个正方体的表面展开图如图2所示,每一个面上都写有一个整数,并且相对两个面上所写的两个整数之和都相等,那么
( )
A.a=1,b=5
B.a=5,b=1
C.a=11,b=5
D.a=5,b=11
图2
图3
3.如图3所示,∠BAC=90°,AD⊥BC,则下列结论中正确的个数是
( )
①点B到AC的垂线段是线段AB;
②线段AC是点C到AB的垂线段;
③线段AD是点D到BC的垂线段;
④线段BD是点B到AD的垂线段.
A.4
B.3
C.2
D.1
4.用一副三角尺不能画出的角(不含平角)的度数是
( )
A.75°
B.135°
C.145°
D.165°
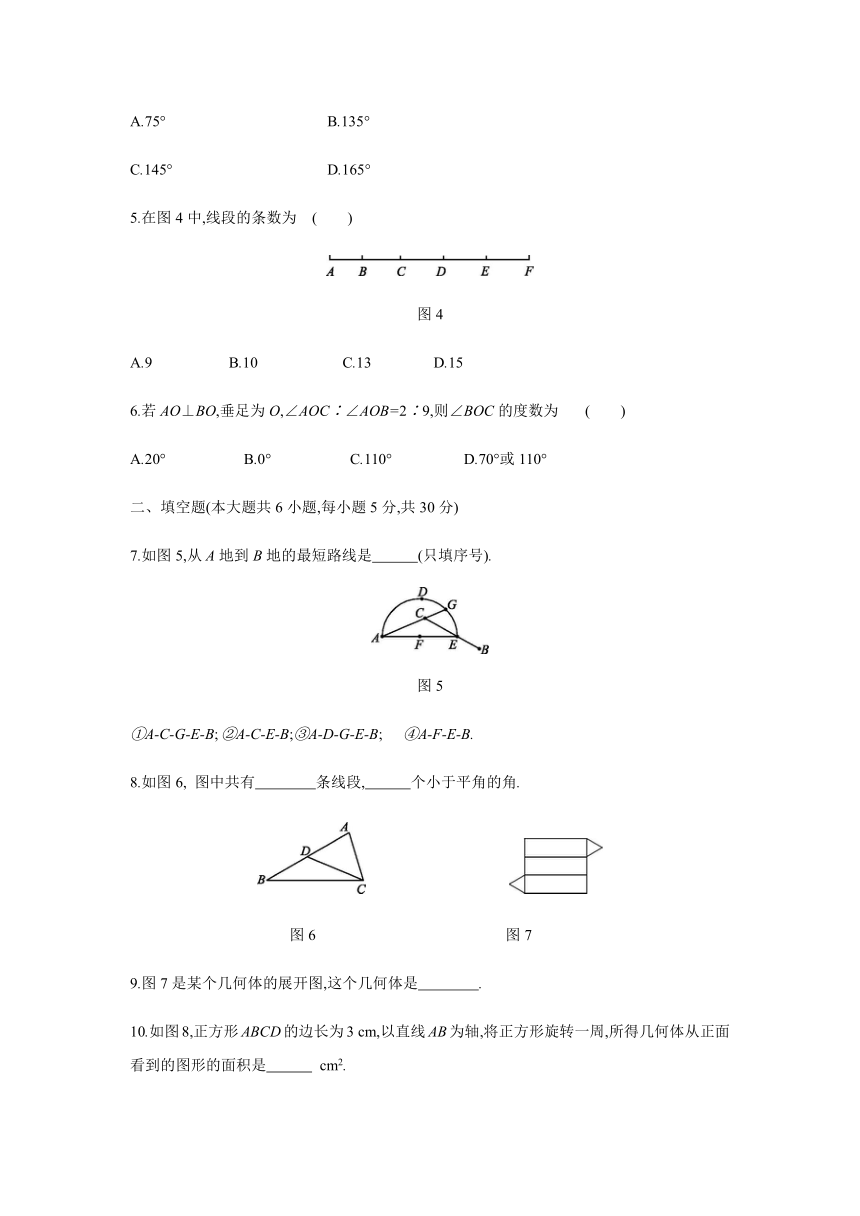
5.在图4中,线段的条数为
( )
图4
A.9
B.10
C.13
D.15
6.若AO⊥BO,垂足为O,∠AOC∶∠AOB=2∶9,则∠BOC的度数为
( )
A.20°
B.0°
C.110°
D.70°或110°
二、填空题(本大题共6小题,每小题5分,共30分)
7.如图5,从A地到B地的最短路线是 (只填序号).?
图5
①A-C-G-E-B;
②A-C-E-B;③A-D-G-E-B;
④A-F-E-B.
8.如图6,
图中共有 条线段, 个小于平角的角.?
图6
图7
9.图7是某个几何体的展开图,这个几何体是 .?
10.如图8,正方形ABCD的边长为3
cm,以直线AB为轴,将正方形旋转一周,所得几何体从正面看到的图形的面积是
cm2.
?
图8
11.如图9,点C在线段AB上,M是线段AC的中点,N是线段BC的中点,且AM=5
cm,CN=
3
cm,则线段AB的长为 cm.?
图9
12.如图10,直线AB,CD交于点O,OE平分∠AOD,∠EOF=90°,∠BOC=80°,则
∠DOF= °.?
图10
三、解答题(本大题共6小题,共46分)
13.(6分)计算:
(1)49.9°= ° ';?
(2)25°42'= °;?
(3)18°46'55″+27°17'24″= .?
14.(6分)如图11,直线AB,CD,EF都经过点O,且AB⊥CD,∠COE=35°,求∠BOE,∠AOE的度数.
图11
15.(8分)如图12,已知C是AB的中点,D是AC的中点,E是BC的中点.
(1)若DE=9
cm,求AB的长;
(2)若CE=5
cm,求DB的长.
图12
16.(8分)已知∠AOB,
如图13,用三角尺和量角器画图.
(1)画∠AOB的平分线OC,并在OC上任取一点P;
(2)过点P画一条平行于OB的直线;
(3)过点P画PD⊥OA,PE⊥OB,垂足分别为D,E.
图13
17.(8分)如图14,数轴上点A对应的有理数为10,点P以每秒1个单位长度的速度从点A出发,点Q以每秒3个单位长度的速度从原点O出发,且P,Q两点同时向数轴正方向运动,设运动时间为t秒.
(1)当t=2时,P,Q两点对应的有理数分别是 , ,PQ= ;?
(2)当PQ=8时,求t的值.
图14
18.(10分)已知∠AOB,过点O作射线OC,使∠AOC=18°,若∠AOC=∠AOB,OD平分∠BOC,求∠AOD的度数.
答案
1.C
2.A
3.B [解析]
①②④正确.
4.C
5.D
6.D [解析]
OC可能在∠AOB的内部,也可能在∠AOB的外部.
设∠AOC=2x,则∠AOB=9x.
因为AO⊥BO,
所以∠AOB=90°,
所以9x=90°,x=10°,∠AOC=2x=20°.
①如图(a),∠BOC=∠AOB-∠AOC=90°-20°=70°;
②如图(b),∠BOC=∠AOB+∠AOC=90°+20°=110°.
7.④
8.6 7
9.三棱柱
10.18 [解析]
将正方形旋转一周所形成的几何体是圆柱,从正面看圆柱得到的图形是一个长方形,长方形的一边长为3
cm,与其相邻的边长为6
cm,所以面积为18
cm2.
11.16
12.130
13.(1)49 54 (2)25.7 (3)46°4'19″
14.解:因为AB⊥CD,
所以∠AOC=∠BOC=90°.
因为∠COE=35°,
所以∠BOE=90°-35°=55°,
∠AOE=∠AOC+∠COE=90°+35°=125°.
15.解:(1)因为D是AC的中点,E是BC的中点,
所以AC=2CD,BC=2CE,
所以AB=AC+BC=2(CD+CE)=2DE=18(cm).
(2)因为E是BC的中点,
所以BC=2CE=10(cm).
因为C是AB的中点,D是AC的中点,
所以DC=AC=BC=5(cm),
所以DB=DC+BC=15(cm).
16.略
17.[解析]
(1)因为10+2×1=12,3×2=6,
所以当t=2时,P,Q两点对应的有理数分别是12,6,
所以PQ=12-6=6.
解:(1)12 6 6
(2)运动t秒时,OP,OQ的长分别是10+t,3t.
①当点P在点Q右侧时,
因为PQ=8,
所以(10+t)-3t=8,
解得t=1;
②当点P在点Q左侧时,
因为PQ=8,
所以3t-(10+t)=8,
解得t=9.
综上所述,t的值为1或9.
18.解:因为∠AOC=18°,
所以∠AOB=2∠AOC=18°×2=36°.
分两种情况讨论.
若OC在∠AOB内部,∠BOC=18°,
则∠COD=9°,
所以∠AOD=∠AOC+∠COD=27°.
若OC在∠AOB外部,∠BOC=54°,
则∠COD=27°,
所以∠AOD=∠COD-∠AOC=9°.
综上所述,∠AOD的度数为27°或9°.
一、选择题(本大题共6小题,每小题4分,共24分)
1.下列几何体中,同一个几何体从上面看和从正面看得到的图形不同的是
( )
图1
2.一个正方体的表面展开图如图2所示,每一个面上都写有一个整数,并且相对两个面上所写的两个整数之和都相等,那么
( )
A.a=1,b=5
B.a=5,b=1
C.a=11,b=5
D.a=5,b=11
图2
图3
3.如图3所示,∠BAC=90°,AD⊥BC,则下列结论中正确的个数是
( )
①点B到AC的垂线段是线段AB;
②线段AC是点C到AB的垂线段;
③线段AD是点D到BC的垂线段;
④线段BD是点B到AD的垂线段.
A.4
B.3
C.2
D.1
4.用一副三角尺不能画出的角(不含平角)的度数是
( )
A.75°
B.135°
C.145°
D.165°
5.在图4中,线段的条数为
( )
图4
A.9
B.10
C.13
D.15
6.若AO⊥BO,垂足为O,∠AOC∶∠AOB=2∶9,则∠BOC的度数为
( )
A.20°
B.0°
C.110°
D.70°或110°
二、填空题(本大题共6小题,每小题5分,共30分)
7.如图5,从A地到B地的最短路线是 (只填序号).?
图5
①A-C-G-E-B;
②A-C-E-B;③A-D-G-E-B;
④A-F-E-B.
8.如图6,
图中共有 条线段, 个小于平角的角.?
图6
图7
9.图7是某个几何体的展开图,这个几何体是 .?
10.如图8,正方形ABCD的边长为3
cm,以直线AB为轴,将正方形旋转一周,所得几何体从正面看到的图形的面积是
cm2.
?
图8
11.如图9,点C在线段AB上,M是线段AC的中点,N是线段BC的中点,且AM=5
cm,CN=
3
cm,则线段AB的长为 cm.?
图9
12.如图10,直线AB,CD交于点O,OE平分∠AOD,∠EOF=90°,∠BOC=80°,则
∠DOF= °.?
图10
三、解答题(本大题共6小题,共46分)
13.(6分)计算:
(1)49.9°= ° ';?
(2)25°42'= °;?
(3)18°46'55″+27°17'24″= .?
14.(6分)如图11,直线AB,CD,EF都经过点O,且AB⊥CD,∠COE=35°,求∠BOE,∠AOE的度数.
图11
15.(8分)如图12,已知C是AB的中点,D是AC的中点,E是BC的中点.
(1)若DE=9
cm,求AB的长;
(2)若CE=5
cm,求DB的长.
图12
16.(8分)已知∠AOB,
如图13,用三角尺和量角器画图.
(1)画∠AOB的平分线OC,并在OC上任取一点P;
(2)过点P画一条平行于OB的直线;
(3)过点P画PD⊥OA,PE⊥OB,垂足分别为D,E.
图13
17.(8分)如图14,数轴上点A对应的有理数为10,点P以每秒1个单位长度的速度从点A出发,点Q以每秒3个单位长度的速度从原点O出发,且P,Q两点同时向数轴正方向运动,设运动时间为t秒.
(1)当t=2时,P,Q两点对应的有理数分别是 , ,PQ= ;?
(2)当PQ=8时,求t的值.
图14
18.(10分)已知∠AOB,过点O作射线OC,使∠AOC=18°,若∠AOC=∠AOB,OD平分∠BOC,求∠AOD的度数.
答案
1.C
2.A
3.B [解析]
①②④正确.
4.C
5.D
6.D [解析]
OC可能在∠AOB的内部,也可能在∠AOB的外部.
设∠AOC=2x,则∠AOB=9x.
因为AO⊥BO,
所以∠AOB=90°,
所以9x=90°,x=10°,∠AOC=2x=20°.
①如图(a),∠BOC=∠AOB-∠AOC=90°-20°=70°;
②如图(b),∠BOC=∠AOB+∠AOC=90°+20°=110°.
7.④
8.6 7
9.三棱柱
10.18 [解析]
将正方形旋转一周所形成的几何体是圆柱,从正面看圆柱得到的图形是一个长方形,长方形的一边长为3
cm,与其相邻的边长为6
cm,所以面积为18
cm2.
11.16
12.130
13.(1)49 54 (2)25.7 (3)46°4'19″
14.解:因为AB⊥CD,
所以∠AOC=∠BOC=90°.
因为∠COE=35°,
所以∠BOE=90°-35°=55°,
∠AOE=∠AOC+∠COE=90°+35°=125°.
15.解:(1)因为D是AC的中点,E是BC的中点,
所以AC=2CD,BC=2CE,
所以AB=AC+BC=2(CD+CE)=2DE=18(cm).
(2)因为E是BC的中点,
所以BC=2CE=10(cm).
因为C是AB的中点,D是AC的中点,
所以DC=AC=BC=5(cm),
所以DB=DC+BC=15(cm).
16.略
17.[解析]
(1)因为10+2×1=12,3×2=6,
所以当t=2时,P,Q两点对应的有理数分别是12,6,
所以PQ=12-6=6.
解:(1)12 6 6
(2)运动t秒时,OP,OQ的长分别是10+t,3t.
①当点P在点Q右侧时,
因为PQ=8,
所以(10+t)-3t=8,
解得t=1;
②当点P在点Q左侧时,
因为PQ=8,
所以3t-(10+t)=8,
解得t=9.
综上所述,t的值为1或9.
18.解:因为∠AOC=18°,
所以∠AOB=2∠AOC=18°×2=36°.
分两种情况讨论.
若OC在∠AOB内部,∠BOC=18°,
则∠COD=9°,
所以∠AOD=∠AOC+∠COD=27°.
若OC在∠AOB外部,∠BOC=54°,
则∠COD=27°,
所以∠AOD=∠COD-∠AOC=9°.
综上所述,∠AOD的度数为27°或9°.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
