2021——2022学年湘教版八年级数学上册第2章 三角形 单元测试题(word版含答案)
文档属性
| 名称 | 2021——2022学年湘教版八年级数学上册第2章 三角形 单元测试题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 151.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览



文档简介
第2章 三角形
一、选择题(每小题3分,共24分)
1.下列各组线段中,不能组成三角形的是
( )
A.6,6,6
B.3,7,5
C.4,5,6
D.3,2,5
2.下列命题中是假命题的是
( )
A.两直线平行,同旁内角互补
B.若两个数的绝对值相等,则这两个数也相等
C.对顶角相等
D.两点之间线段最短
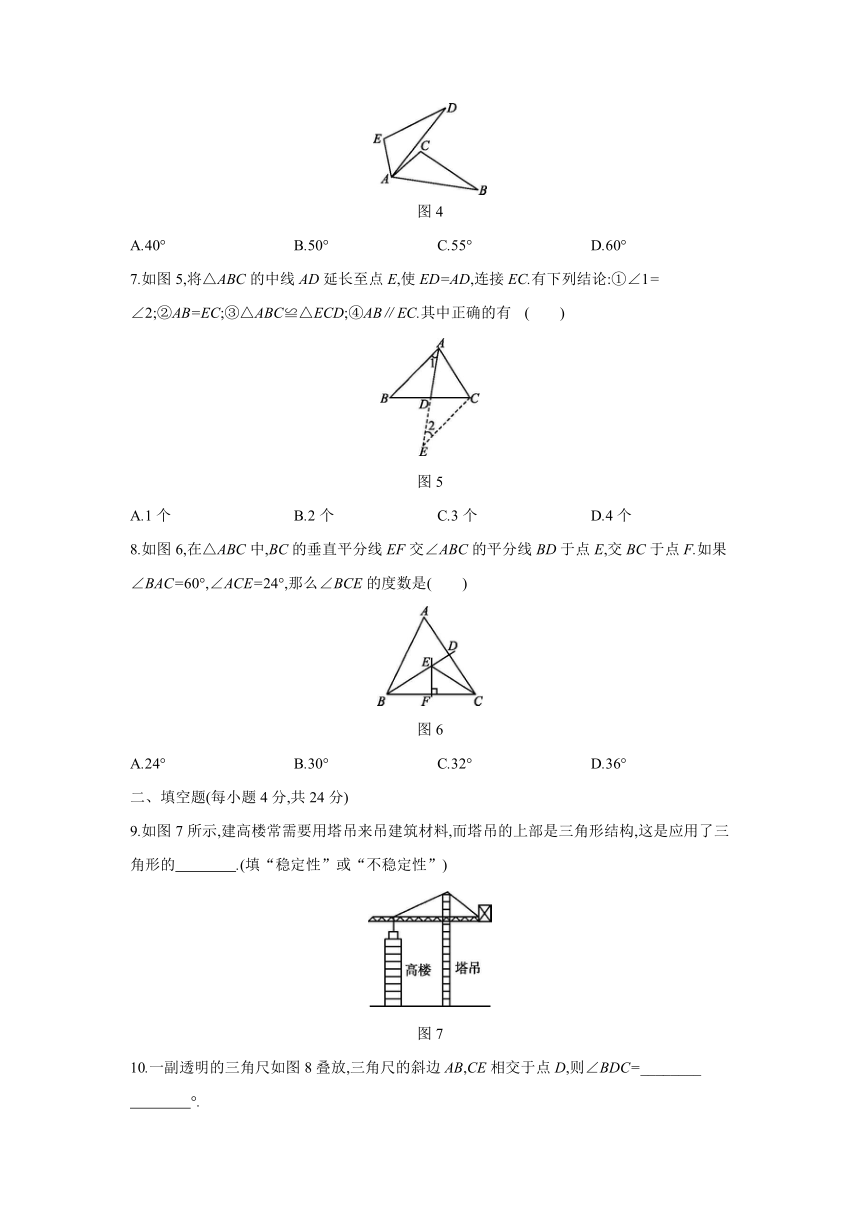
3.如图1,点D,E分别在AB,AC上,CD与BE相交于点O,已知AB=AC,现添加以下条件仍不能判定△ABE≌△ACD的是
( )
图1
A.∠B=∠C
B.BE=CD
C.BD=CE
D.AD=AE
4.如图2,已知射线OM,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,那么∠AOB的度数是
( )
图2
A.90°
B.60°
C.45°
D.30°
5.如图3所示,小敏做《全品作业本》中的习题时,题目中的三角形被涂料弄污了一部分,她想在一块白纸上作一个完全一样的三角形,然后粘贴在上面,她作图的依据是
( )
图3
A.SSS
B.SAS
C.ASA
D.AAS
6.如图4所示,△ABC≌△ADE,且∠B=25°,∠E=105°,∠DAC=10°,则∠EAC的度数为( )
图4
A.40°
B.50°
C.55°
D.60°
7.如图5,将△ABC的中线AD延长至点E,使ED=AD,连接EC.有下列结论:①∠1=
∠2;②AB=EC;③△ABC≌△ECD;④AB∥EC.其中正确的有
( )
图5
A.1个
B.2个
C.3个
D.4个
8.如图6,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于点E,交BC于点F.如果∠BAC=60°,∠ACE=24°,那么∠BCE的度数是( )
图6
A.24°
B.30°
C.32°
D.36°
二、填空题(每小题4分,共24分)
9.如图7所示,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的 .(填“稳定性”或“不稳定性”)?
图7
10.一副透明的三角尺如图8叠放,三角尺的斜边AB,CE相交于点D,则∠BDC=________
°.?
图8
11.把命题“等腰三角形的两底角相等”改写成“如果……,那么……”的形式是______________
.?
12.用反证法证明“直角三角形的两个锐角互余”,应先假设: .?
13.如图9,在△ABC中,AB的垂直平分线ME交BC于点M,交AB于点E,AC的垂直平分线NF交BC于点N,交AC于点F.若BC的长是25,则△AMN的周长是 .?
图9
14.如图10,D是等边三角形ABC外一点,连接AD,BD,CD.若BD=8,CD=6,则AD的最大值与最小值的差为 .?
图10
三、解答题(共52分)
15.(8分)判断下列命题是真命题还是假命题,若是假命题,请举出一个反例说明.
(1)有一个角是60°的等腰三角形是等边三角形;
(2)有两个角是锐角的三角形是锐角三角形.
16.(10分)如图11,在△ABC中,BO,CO分别平分∠ABC,∠ACB,过点O作EF∥BC分别交AB,AC于点E,F.若△AEF的周长为16,BC的长为8,求△ABC的周长.
图11
17.(10分)如图12,∠BAC=∠ABD.
(1)要使OC=OD,可以添加的条件为 或 ;(写出两个符合题意的条件即可)?
(2)请选择(1)中你所添加的一个条件,利用三角形全等证明OC=OD.
图12
18.(12分)如图13,在四边形ABCD中,点E在BC上,点F在ED上,AB=CD,AB∥CD,AD∥BC,∠B=∠AFE,EA是∠BEF的平分线.
求证:(1)△ABE≌△AFE;
(2)∠FAD=∠CDE.
图13
19.(12分)如图14,O是等边三角形ABC内一点,∠AOB=105°,∠BOC=α.在等边三角形ABC外部作线段CD=CO,使得∠OCD=60°,连接AD,OD.
(1)求证:BO=AD;
(2)探究:当α为多少度时,△AOD是等腰三角形?
图14
答案
1.D 2.B
3.B [解析]
由题意知AB=AC,∠A为公共角.A选项,添加∠B=∠C,利用ASA即可证明△ABE≌△ACD;B选项,添加BE=CD,因为SSA不能证明△ABE≌△ACD,所以此选项不能作为添加的条件;C选项,添加BD=CE,由等量关系可得AD=AE,利用SAS即可证明△ABE≌△ACD;D选项,添加AD=AE,利用SAS即可证明△ABE≌△ACD.故选B.
4.B [解析]
连接AB.根据题意,得OB=OA=AB,∴△AOB是等边三角形,∴∠AOB=60°.
5.C 6.D
7.C [解析]
①②④正确.故选C.
8.C [解析]
∵
EF是BC的垂直平分线,
∴BE=CE,∴∠DBC=∠ECB.
∵BD是∠ABC的平分线,
∴∠ABD=∠DBC,
∴∠ABD=∠DBC=∠ECB.
∵∠BAC=60°,∠ACE=24°,
∴∠ABD=∠DBC=∠ECB=×(180°-60°-24°)=32°.故选C.
9.稳定性
10.75
[解析]
∵∠CEA=60°,∠BAE=45°,∴∠ADE=180°-∠CEA-∠BAE=75°,∴∠BDC=
∠ADE=75°.
11.如果一个三角形是等腰三角形,那么它的两底角相等
12.直角三角形的两个锐角不互余
13.25
14.12 [解析]
如图,以CD为边向外作等边三角形CDE,连接BE.
∵△CDE和△ABC都是等边三角形,
∴DE=CE=CD,CB=CA,∠ECD=∠BCA=60°,
∴∠ECD+∠BCD=∠BCA+∠BCD,
即∠ECB=∠DCA.
在△ECB和△DCA中,
∴△ECB≌△DCA(SAS),
∴BE=AD.
∵DE=CD=6,BD=8,
∴BD-DE≤BE≤BD+DE,
即8-6≤BE≤8+6,
∴2≤BE≤14,
∴2≤AD≤14.
当B,D,E三点共线时,可得BE的最大值与最小值分别为14和2,
∴AD的最大值与最小值的差为14-2=12.
故答案为12.
15.解:(1)真命题.
(2)假命题.反例:在△ABC中,∠A=20°,∠B=30°,这时∠C=130°,△ABC是钝角三角形,所以原命题为假命题.
16.解:∵BO平分∠ABC,
∴∠ABO=∠CBO.
∵EF∥BC,
∴∠CBO=∠EOB,
∴∠ABO=∠EOB,
∴BE=OE.
同理可得CF=OF.
∵△AEF的周长为16,
∴AE+OE+OF+AF=AE+BE+CF+AF=AB+AC=16.
又∵BC=8,∴△ABC的周长为16+8=24.
17.解:(1)答案不唯一,如∠C=∠D或∠ABC=∠BAD或∠OAD=∠OBC或AC=BD(从中选两个即可)
(2)答案不唯一,如选AC=BD.证明如下:
在△ABD和△BAC中,
∴△ABD≌△BAC,
∴AD=BC,∠D=∠C.
在△BOC和△AOD中,
∴△BOC≌△AOD,∴OC=OD.
18.证明:(1)∵EA是∠BEF的平分线,
∴∠AEB=∠AEF.
在△ABE和△AFE中,
∴△ABE≌△AFE(AAS).
(2)∵△ABE≌△AFE,
∴AB=AF.
又∵AB=CD,
∴AF=CD.
∵AD∥BC,
∴∠ADF=∠DEC.
∵AB∥CD,
∴∠B+∠C=180°.
∵∠B=∠AFE,∠AFE+∠AFD=180°,
∴∠AFD=∠C.
在△AFD和△DCE中,
∴△AFD≌△DCE(AAS),
∴∠FAD=∠CDE.
19.解:(1)证明:∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠OCD=60°=∠ACB,
∴∠OCD-∠OCA=∠ACB-∠OCA,
即∠ACD=∠BCO.
在△ADC与△BOC中,
∴△ADC≌△BOC,
∴BO=AD.
(2)由(1)可知△ADC≌△BOC,
∴∠ADC=∠BOC=α.
∵CD=CO,∠OCD=60°,
∴△DCO为等边三角形,
∴∠ODC=∠DOC=60°,
∴∠ADO=α-60°,
∠AOD=360°-60°-105°-α=195°-α.
若△AOD为等腰三角形,则应分类讨论:
①若∠AOD=∠ADO,则195°-α=α-60°,解得α=127.5°.
②若∠AOD=∠DAO,则2(195°-α)+α-60°=180°,解得α=150°.
③若∠ADO=∠DAO,则2(α-60°)+195°-α=180°,解得α=105°.
综上,当α为127.5°,150°或105°时,△AOD为等腰三角形.
一、选择题(每小题3分,共24分)
1.下列各组线段中,不能组成三角形的是
( )
A.6,6,6
B.3,7,5
C.4,5,6
D.3,2,5
2.下列命题中是假命题的是
( )
A.两直线平行,同旁内角互补
B.若两个数的绝对值相等,则这两个数也相等
C.对顶角相等
D.两点之间线段最短
3.如图1,点D,E分别在AB,AC上,CD与BE相交于点O,已知AB=AC,现添加以下条件仍不能判定△ABE≌△ACD的是
( )
图1
A.∠B=∠C
B.BE=CD
C.BD=CE
D.AD=AE
4.如图2,已知射线OM,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,那么∠AOB的度数是
( )
图2
A.90°
B.60°
C.45°
D.30°
5.如图3所示,小敏做《全品作业本》中的习题时,题目中的三角形被涂料弄污了一部分,她想在一块白纸上作一个完全一样的三角形,然后粘贴在上面,她作图的依据是
( )
图3
A.SSS
B.SAS
C.ASA
D.AAS
6.如图4所示,△ABC≌△ADE,且∠B=25°,∠E=105°,∠DAC=10°,则∠EAC的度数为( )
图4
A.40°
B.50°
C.55°
D.60°
7.如图5,将△ABC的中线AD延长至点E,使ED=AD,连接EC.有下列结论:①∠1=
∠2;②AB=EC;③△ABC≌△ECD;④AB∥EC.其中正确的有
( )
图5
A.1个
B.2个
C.3个
D.4个
8.如图6,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于点E,交BC于点F.如果∠BAC=60°,∠ACE=24°,那么∠BCE的度数是( )
图6
A.24°
B.30°
C.32°
D.36°
二、填空题(每小题4分,共24分)
9.如图7所示,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的 .(填“稳定性”或“不稳定性”)?
图7
10.一副透明的三角尺如图8叠放,三角尺的斜边AB,CE相交于点D,则∠BDC=________
°.?
图8
11.把命题“等腰三角形的两底角相等”改写成“如果……,那么……”的形式是______________
.?
12.用反证法证明“直角三角形的两个锐角互余”,应先假设: .?
13.如图9,在△ABC中,AB的垂直平分线ME交BC于点M,交AB于点E,AC的垂直平分线NF交BC于点N,交AC于点F.若BC的长是25,则△AMN的周长是 .?
图9
14.如图10,D是等边三角形ABC外一点,连接AD,BD,CD.若BD=8,CD=6,则AD的最大值与最小值的差为 .?
图10
三、解答题(共52分)
15.(8分)判断下列命题是真命题还是假命题,若是假命题,请举出一个反例说明.
(1)有一个角是60°的等腰三角形是等边三角形;
(2)有两个角是锐角的三角形是锐角三角形.
16.(10分)如图11,在△ABC中,BO,CO分别平分∠ABC,∠ACB,过点O作EF∥BC分别交AB,AC于点E,F.若△AEF的周长为16,BC的长为8,求△ABC的周长.
图11
17.(10分)如图12,∠BAC=∠ABD.
(1)要使OC=OD,可以添加的条件为 或 ;(写出两个符合题意的条件即可)?
(2)请选择(1)中你所添加的一个条件,利用三角形全等证明OC=OD.
图12
18.(12分)如图13,在四边形ABCD中,点E在BC上,点F在ED上,AB=CD,AB∥CD,AD∥BC,∠B=∠AFE,EA是∠BEF的平分线.
求证:(1)△ABE≌△AFE;
(2)∠FAD=∠CDE.
图13
19.(12分)如图14,O是等边三角形ABC内一点,∠AOB=105°,∠BOC=α.在等边三角形ABC外部作线段CD=CO,使得∠OCD=60°,连接AD,OD.
(1)求证:BO=AD;
(2)探究:当α为多少度时,△AOD是等腰三角形?
图14
答案
1.D 2.B
3.B [解析]
由题意知AB=AC,∠A为公共角.A选项,添加∠B=∠C,利用ASA即可证明△ABE≌△ACD;B选项,添加BE=CD,因为SSA不能证明△ABE≌△ACD,所以此选项不能作为添加的条件;C选项,添加BD=CE,由等量关系可得AD=AE,利用SAS即可证明△ABE≌△ACD;D选项,添加AD=AE,利用SAS即可证明△ABE≌△ACD.故选B.
4.B [解析]
连接AB.根据题意,得OB=OA=AB,∴△AOB是等边三角形,∴∠AOB=60°.
5.C 6.D
7.C [解析]
①②④正确.故选C.
8.C [解析]
∵
EF是BC的垂直平分线,
∴BE=CE,∴∠DBC=∠ECB.
∵BD是∠ABC的平分线,
∴∠ABD=∠DBC,
∴∠ABD=∠DBC=∠ECB.
∵∠BAC=60°,∠ACE=24°,
∴∠ABD=∠DBC=∠ECB=×(180°-60°-24°)=32°.故选C.
9.稳定性
10.75
[解析]
∵∠CEA=60°,∠BAE=45°,∴∠ADE=180°-∠CEA-∠BAE=75°,∴∠BDC=
∠ADE=75°.
11.如果一个三角形是等腰三角形,那么它的两底角相等
12.直角三角形的两个锐角不互余
13.25
14.12 [解析]
如图,以CD为边向外作等边三角形CDE,连接BE.
∵△CDE和△ABC都是等边三角形,
∴DE=CE=CD,CB=CA,∠ECD=∠BCA=60°,
∴∠ECD+∠BCD=∠BCA+∠BCD,
即∠ECB=∠DCA.
在△ECB和△DCA中,
∴△ECB≌△DCA(SAS),
∴BE=AD.
∵DE=CD=6,BD=8,
∴BD-DE≤BE≤BD+DE,
即8-6≤BE≤8+6,
∴2≤BE≤14,
∴2≤AD≤14.
当B,D,E三点共线时,可得BE的最大值与最小值分别为14和2,
∴AD的最大值与最小值的差为14-2=12.
故答案为12.
15.解:(1)真命题.
(2)假命题.反例:在△ABC中,∠A=20°,∠B=30°,这时∠C=130°,△ABC是钝角三角形,所以原命题为假命题.
16.解:∵BO平分∠ABC,
∴∠ABO=∠CBO.
∵EF∥BC,
∴∠CBO=∠EOB,
∴∠ABO=∠EOB,
∴BE=OE.
同理可得CF=OF.
∵△AEF的周长为16,
∴AE+OE+OF+AF=AE+BE+CF+AF=AB+AC=16.
又∵BC=8,∴△ABC的周长为16+8=24.
17.解:(1)答案不唯一,如∠C=∠D或∠ABC=∠BAD或∠OAD=∠OBC或AC=BD(从中选两个即可)
(2)答案不唯一,如选AC=BD.证明如下:
在△ABD和△BAC中,
∴△ABD≌△BAC,
∴AD=BC,∠D=∠C.
在△BOC和△AOD中,
∴△BOC≌△AOD,∴OC=OD.
18.证明:(1)∵EA是∠BEF的平分线,
∴∠AEB=∠AEF.
在△ABE和△AFE中,
∴△ABE≌△AFE(AAS).
(2)∵△ABE≌△AFE,
∴AB=AF.
又∵AB=CD,
∴AF=CD.
∵AD∥BC,
∴∠ADF=∠DEC.
∵AB∥CD,
∴∠B+∠C=180°.
∵∠B=∠AFE,∠AFE+∠AFD=180°,
∴∠AFD=∠C.
在△AFD和△DCE中,
∴△AFD≌△DCE(AAS),
∴∠FAD=∠CDE.
19.解:(1)证明:∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠OCD=60°=∠ACB,
∴∠OCD-∠OCA=∠ACB-∠OCA,
即∠ACD=∠BCO.
在△ADC与△BOC中,
∴△ADC≌△BOC,
∴BO=AD.
(2)由(1)可知△ADC≌△BOC,
∴∠ADC=∠BOC=α.
∵CD=CO,∠OCD=60°,
∴△DCO为等边三角形,
∴∠ODC=∠DOC=60°,
∴∠ADO=α-60°,
∠AOD=360°-60°-105°-α=195°-α.
若△AOD为等腰三角形,则应分类讨论:
①若∠AOD=∠ADO,则195°-α=α-60°,解得α=127.5°.
②若∠AOD=∠DAO,则2(195°-α)+α-60°=180°,解得α=150°.
③若∠ADO=∠DAO,则2(α-60°)+195°-α=180°,解得α=105°.
综上,当α为127.5°,150°或105°时,△AOD为等腰三角形.
同课章节目录
