合情推理课件(新课标A)
图片预览











文档简介
(共40张PPT)
福尔摩斯
柯南
4.今夜恰有东风
1.今夜恰有大雾
2.曹操生性多疑
3.北军不善水战
弓弩利于远战
草船借箭必将成功
我们来推测诸葛亮“先生”的推理过程:
根据一个或几个已知的判断来确定一个新的判断的思维过程就叫推理.
已知
判断
前提
新的
判断
结论
2.由三角形内角和为 ,凸四边形内角和为 ,凸五边形内角和为 ,
1.由铜、铁、铝、金、银等金属都能导电,
3.地球上有生命,火星具有一些与地球类
似的特征,
4.因为所有人都会死,苏格拉底是人,
猜想:一切金属都能导电.
猜想:凸n边形内角和为
猜想:火星上也有生命.
所以苏格拉底会死.
归纳推理
类比推理
合情推理
演绎推理
2.1.1 合情推理
学习目标:
1.理解合情推理的含义,利用归纳推理进行简单的推理,体会
并认识合情推理在数学发现中的作用。
2.理解类比推理的概念,利用类比推理进行简单的推理,掌握类比
推理解决问题的思路。
重点与难点
1.重点是理解归纳类比推理的概念,能利用归纳类比的方法
进行简单的推理。
2.难点是利用归纳类比进行推理及探索问题。
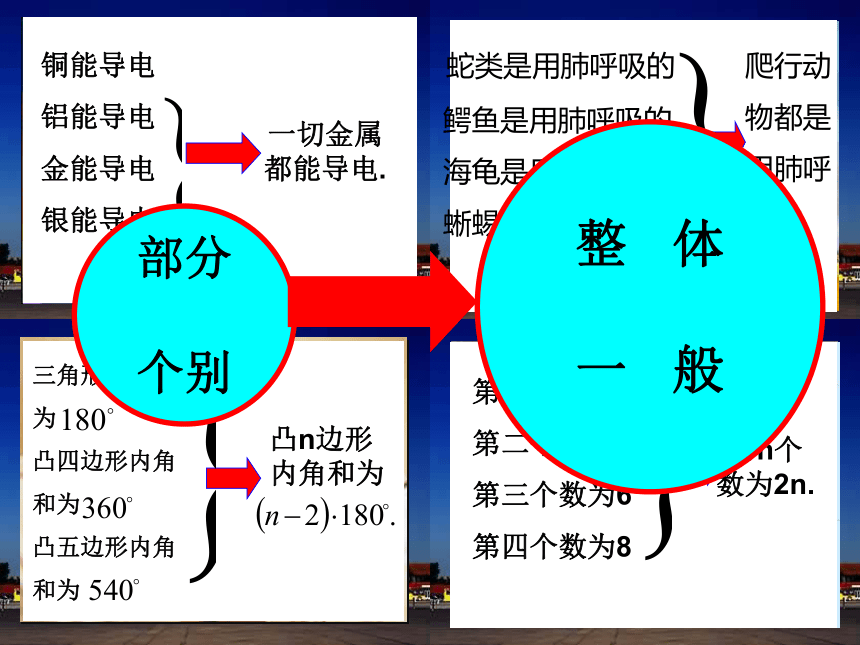
铜能导电
铝能导电
金能导电
银能导电
一切金属都能导电.
三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
凸n边形内角和为
第一个数为2
第二个数为4
第三个数为6
第四个数为8
第n个数为2n.
部分
个别
蛇类是用肺呼吸的
鳄鱼是用肺呼吸的
海龟是用肺呼吸的
蜥蜴是用肺呼吸的
爬行动
物都是
用肺呼
吸的
整 体
一 般
由某类事物的 具有某些特征,推出该类事物的 都具有这些特征的推理,或者由 概括出 的推理,称为归纳推理(简称归纳).
部分对象
全部对象
个别事实
一般结论
由某类事物的 具有某些特征,推出该类事物的 都具有这些特征的推理,或者由 概括出 的推理,称为归纳推理(简称归纳).
部分对象
全部对象
个别事实
一般结论
你能举出归纳推理的例子吗
即是由部分到整体,由个别到一般的推理.
观察下列等式
6=3+3,
8=3+5,
10=3+7,
归纳出一个规律:
偶数=奇质数+奇质数
通过更多特例的检验,从6开始,没有出现反例.
大胆猜想:
任何一个不小于6的偶数都等于两个奇质数的和.
12=5+7,
14=3+11,
16=5+11
陈氏定理
应用归纳推理可以
发现新事实,获得新结论!
歌德巴赫猜想
四色定理
牛顿发现万有引力
门捷列夫发现元素周期律等等
1.对于数列1,3,5,7,…,由此你猜想出第 个数是____ .
2.观察右图,可以发现: _____________________.
1=12,
1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
1+3+5+7+9=25=52,
……
(第2题)
思考题组一:
3.对任意的正整数 ,猜想 与 的大小关系.
一种有趣且有很长历史的数叫费马素数,这些数是由法国数学家费马在研究数列
的前五项:
发现它们都是素数,于是费马就猜想:形如 的数都是素数。
费马素数猜想
否定一个猜想只需举出一个反例即可!
——一个错误的猜想
另外,德国数学家希尔伯特1900年在巴黎提出的著名的“希尔伯特23个问题”。有的尚未解决,但却极大地促进了数学这门学科的发展和健全.
实验观察
大胆猜想
验证猜想
归纳推理的过程:
(1)从特殊到一般;
归纳推理的特点:
合情推理是冒险的,有争议的和暂时的.
--波利亚
(3)具有或然性。
(2)具有创造性;
1.已知数列{ }的第一项 =1,
且 ( =1,2,3,···),
请归纳出这个数列的通项公式为________.
思考题组二:
任取两条平行线 ,在直线 上任取三个点依次记作 ,在直线 上任取三个点依次记作 .连接 ,记交点为 ;连接 ,记交点为 ;连接 ,记交点为 .你能发现什么规律呢
2.
传说在古老的印度有一座神庙,神庙中有三根针和套在一根针上的64个圆环.古印度的天神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了.
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次
1
2
3
1
2
3
第1个圆环从1到3.
设 为把 个圆环从1号针移到3号针的最少次数,则
=1时,
=1
=2时,
1
2
3
第1个圆环从1到3.
前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.
设 为把 个圆环从1号针移到3号针的最少次数,则
=1
=1时,
=3
=2时, =3
=1时, =1
=3时,
1
2
3
第1个圆环从1到3.
前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.
前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.
设 为把 个圆环从1号针移到3号针的最少次数,则
=7
根据以上分析,我们可得以下递推公式
从这个递推公式出发,可以证明上述通项公式是正确的.
从 ,我们猜想其通项公式为
例2.数一数图中的凸多面体的面数F、顶点数V和棱数E,然后探求面数F、顶点数V和棱数E之间的关系.
四棱柱
三棱锥
八面体
三棱柱
四棱锥
尖顶塔
6
9
5
9
5
5
8
16
9
凸多面体 面数(F) 顶点数(V) 棱数(E)
四棱柱
三棱锥
八面体
三棱柱
四棱锥
尖顶塔
6
8
12
6
4
4
12
8
6
猜想凸多面体的面数F、顶点数V和棱数E之间的关系式为:
F+V-E=2
欧拉公式
可能有生命存在
有生命存在
温度适合生物的生存
一年中有四季的变更
有大气层
大部分时间的温度适合地球上某些已知生物的生存
一年中有四季的变更
有大气层
行星、围绕太阳运行、绕轴自转
行星、围绕太阳运行、绕轴自转
火星
地球
火星与地球类比的思维过程:
火星
地球
存在类似特征
有生命存在
猜测火星上也可能有生命存在
由两类对象具有某些类似特征和其中
一类对象的某些已知特征,推出另一类对
象也具有这些特征的推理称为类比推理.
试举出其他类比的例子
类比推理的结论不一定成立.
我们已经学习过“等差数列”与“等比数列”.你是否想过“等和数列”、“等积数列” ?
从第二项起,每一项与其前一项的差(比)等于同一个常数的数列是等差(比)数列.
类推
从第二项起,每一项与其前一项的和(积)等于同一个常数的数列是等和(积)数列.
在平面内,若a⊥c,b⊥c,则a//b.类比地推广到空间,你会得到什么结论?并判断正误。
在空间中,若α ⊥γ,β ⊥γ则α//β。
错误
例3 根据等式的性质,猜想不等式的性质
等式的性质
不等式的性质
.
.
弦
直径
周长
面积
截面圆
经过球心的截面圆
表面积
体积
圆的概念和性质 球的类似概念和性质
圆心与弦(非直径)中点连线垂直于弦.
与圆心距离相等的两弦相等;与圆心距离不等的两弦不等,距圆心较近的弦较长.
以点P(x0,y0,)为圆心,以r为半径的圆的方程为
(x-x0)2+(y-y0)2=r2.
球心与截面圆(不经过球心的截面圆)圆心连线垂直于截面圆.
与球心距离相等的两截面圆面积相等;与球心距离不等的两截面圆面积不等,距球心较近的截面圆面积较大.
以点P(x0,y0,z0)为球心,r为半径的球的方程为
(x-x0)2+(y-y0)2+(z-z0)2=r2.
幻灯片 31球
例4:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.
A
B
C
a
b
c
o
A
B
C
s1
s2
s3
c2=a2+b2
S2△ABC =S2△AOB+S2△AOC+S2△BOC
猜想:
课下思考:
类比平面内三角形的余弦定理,试给出空间中四面体性质的猜想.
A
B
C
B
C
D
V
类比推理
由特殊到特殊的推理;
以旧的知识为基础,推测新的结果;
结论不一定成立.
归纳推理
由部分到整体、特殊到一般的推理;
以观察分析为基础,推测新的结论;
具有发现的功能;
结论不一定成立.
具有发现的功能;
通俗地说,合情推理是指“合乎情理”的推理.
合情推理
归纳推理
类比推理
作 业
1、作业本:2.1.1合情推理(一)
2、实习作业:(利用网络资源)
孪生素数猜想 ;叙拉古猜想 ; 蜂窝猜想; 费马最后定理;七桥问题;欧拉回路
探究题:
数列 满足 ,
猜想此数列的通项公式.
猜想:
福尔摩斯
柯南
4.今夜恰有东风
1.今夜恰有大雾
2.曹操生性多疑
3.北军不善水战
弓弩利于远战
草船借箭必将成功
我们来推测诸葛亮“先生”的推理过程:
根据一个或几个已知的判断来确定一个新的判断的思维过程就叫推理.
已知
判断
前提
新的
判断
结论
2.由三角形内角和为 ,凸四边形内角和为 ,凸五边形内角和为 ,
1.由铜、铁、铝、金、银等金属都能导电,
3.地球上有生命,火星具有一些与地球类
似的特征,
4.因为所有人都会死,苏格拉底是人,
猜想:一切金属都能导电.
猜想:凸n边形内角和为
猜想:火星上也有生命.
所以苏格拉底会死.
归纳推理
类比推理
合情推理
演绎推理
2.1.1 合情推理
学习目标:
1.理解合情推理的含义,利用归纳推理进行简单的推理,体会
并认识合情推理在数学发现中的作用。
2.理解类比推理的概念,利用类比推理进行简单的推理,掌握类比
推理解决问题的思路。
重点与难点
1.重点是理解归纳类比推理的概念,能利用归纳类比的方法
进行简单的推理。
2.难点是利用归纳类比进行推理及探索问题。
铜能导电
铝能导电
金能导电
银能导电
一切金属都能导电.
三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
凸n边形内角和为
第一个数为2
第二个数为4
第三个数为6
第四个数为8
第n个数为2n.
部分
个别
蛇类是用肺呼吸的
鳄鱼是用肺呼吸的
海龟是用肺呼吸的
蜥蜴是用肺呼吸的
爬行动
物都是
用肺呼
吸的
整 体
一 般
由某类事物的 具有某些特征,推出该类事物的 都具有这些特征的推理,或者由 概括出 的推理,称为归纳推理(简称归纳).
部分对象
全部对象
个别事实
一般结论
由某类事物的 具有某些特征,推出该类事物的 都具有这些特征的推理,或者由 概括出 的推理,称为归纳推理(简称归纳).
部分对象
全部对象
个别事实
一般结论
你能举出归纳推理的例子吗
即是由部分到整体,由个别到一般的推理.
观察下列等式
6=3+3,
8=3+5,
10=3+7,
归纳出一个规律:
偶数=奇质数+奇质数
通过更多特例的检验,从6开始,没有出现反例.
大胆猜想:
任何一个不小于6的偶数都等于两个奇质数的和.
12=5+7,
14=3+11,
16=5+11
陈氏定理
应用归纳推理可以
发现新事实,获得新结论!
歌德巴赫猜想
四色定理
牛顿发现万有引力
门捷列夫发现元素周期律等等
1.对于数列1,3,5,7,…,由此你猜想出第 个数是____ .
2.观察右图,可以发现: _____________________.
1=12,
1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
1+3+5+7+9=25=52,
……
(第2题)
思考题组一:
3.对任意的正整数 ,猜想 与 的大小关系.
一种有趣且有很长历史的数叫费马素数,这些数是由法国数学家费马在研究数列
的前五项:
发现它们都是素数,于是费马就猜想:形如 的数都是素数。
费马素数猜想
否定一个猜想只需举出一个反例即可!
——一个错误的猜想
另外,德国数学家希尔伯特1900年在巴黎提出的著名的“希尔伯特23个问题”。有的尚未解决,但却极大地促进了数学这门学科的发展和健全.
实验观察
大胆猜想
验证猜想
归纳推理的过程:
(1)从特殊到一般;
归纳推理的特点:
合情推理是冒险的,有争议的和暂时的.
--波利亚
(3)具有或然性。
(2)具有创造性;
1.已知数列{ }的第一项 =1,
且 ( =1,2,3,···),
请归纳出这个数列的通项公式为________.
思考题组二:
任取两条平行线 ,在直线 上任取三个点依次记作 ,在直线 上任取三个点依次记作 .连接 ,记交点为 ;连接 ,记交点为 ;连接 ,记交点为 .你能发现什么规律呢
2.
传说在古老的印度有一座神庙,神庙中有三根针和套在一根针上的64个圆环.古印度的天神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了.
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次
1
2
3
1
2
3
第1个圆环从1到3.
设 为把 个圆环从1号针移到3号针的最少次数,则
=1时,
=1
=2时,
1
2
3
第1个圆环从1到3.
前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.
设 为把 个圆环从1号针移到3号针的最少次数,则
=1
=1时,
=3
=2时, =3
=1时, =1
=3时,
1
2
3
第1个圆环从1到3.
前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.
前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.
设 为把 个圆环从1号针移到3号针的最少次数,则
=7
根据以上分析,我们可得以下递推公式
从这个递推公式出发,可以证明上述通项公式是正确的.
从 ,我们猜想其通项公式为
例2.数一数图中的凸多面体的面数F、顶点数V和棱数E,然后探求面数F、顶点数V和棱数E之间的关系.
四棱柱
三棱锥
八面体
三棱柱
四棱锥
尖顶塔
6
9
5
9
5
5
8
16
9
凸多面体 面数(F) 顶点数(V) 棱数(E)
四棱柱
三棱锥
八面体
三棱柱
四棱锥
尖顶塔
6
8
12
6
4
4
12
8
6
猜想凸多面体的面数F、顶点数V和棱数E之间的关系式为:
F+V-E=2
欧拉公式
可能有生命存在
有生命存在
温度适合生物的生存
一年中有四季的变更
有大气层
大部分时间的温度适合地球上某些已知生物的生存
一年中有四季的变更
有大气层
行星、围绕太阳运行、绕轴自转
行星、围绕太阳运行、绕轴自转
火星
地球
火星与地球类比的思维过程:
火星
地球
存在类似特征
有生命存在
猜测火星上也可能有生命存在
由两类对象具有某些类似特征和其中
一类对象的某些已知特征,推出另一类对
象也具有这些特征的推理称为类比推理.
试举出其他类比的例子
类比推理的结论不一定成立.
我们已经学习过“等差数列”与“等比数列”.你是否想过“等和数列”、“等积数列” ?
从第二项起,每一项与其前一项的差(比)等于同一个常数的数列是等差(比)数列.
类推
从第二项起,每一项与其前一项的和(积)等于同一个常数的数列是等和(积)数列.
在平面内,若a⊥c,b⊥c,则a//b.类比地推广到空间,你会得到什么结论?并判断正误。
在空间中,若α ⊥γ,β ⊥γ则α//β。
错误
例3 根据等式的性质,猜想不等式的性质
等式的性质
不等式的性质
.
.
弦
直径
周长
面积
截面圆
经过球心的截面圆
表面积
体积
圆的概念和性质 球的类似概念和性质
圆心与弦(非直径)中点连线垂直于弦.
与圆心距离相等的两弦相等;与圆心距离不等的两弦不等,距圆心较近的弦较长.
以点P(x0,y0,)为圆心,以r为半径的圆的方程为
(x-x0)2+(y-y0)2=r2.
球心与截面圆(不经过球心的截面圆)圆心连线垂直于截面圆.
与球心距离相等的两截面圆面积相等;与球心距离不等的两截面圆面积不等,距球心较近的截面圆面积较大.
以点P(x0,y0,z0)为球心,r为半径的球的方程为
(x-x0)2+(y-y0)2+(z-z0)2=r2.
幻灯片 31球
例4:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.
A
B
C
a
b
c
o
A
B
C
s1
s2
s3
c2=a2+b2
S2△ABC =S2△AOB+S2△AOC+S2△BOC
猜想:
课下思考:
类比平面内三角形的余弦定理,试给出空间中四面体性质的猜想.
A
B
C
B
C
D
V
类比推理
由特殊到特殊的推理;
以旧的知识为基础,推测新的结果;
结论不一定成立.
归纳推理
由部分到整体、特殊到一般的推理;
以观察分析为基础,推测新的结论;
具有发现的功能;
结论不一定成立.
具有发现的功能;
通俗地说,合情推理是指“合乎情理”的推理.
合情推理
归纳推理
类比推理
作 业
1、作业本:2.1.1合情推理(一)
2、实习作业:(利用网络资源)
孪生素数猜想 ;叙拉古猜想 ; 蜂窝猜想; 费马最后定理;七桥问题;欧拉回路
探究题:
数列 满足 ,
猜想此数列的通项公式.
猜想:
