2.6 利用三角函数测高 课件(共18张PPT)
文档属性
| 名称 | 2.6 利用三角函数测高 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览






文档简介
第二章 直角三角形的边角关系
6 利用三角函数测高
知识点 利用三角函数测高
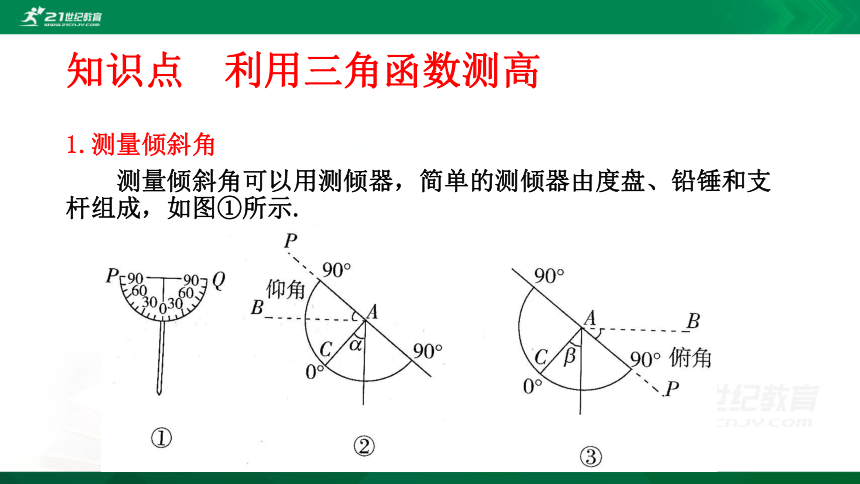
1.测量倾斜角
测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成,如图①所示.
使用测倾器测量倾斜角的步骤如下:
(1)把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
(2)转动度盘,使度盘的直径对准目标,记下此时铅垂线所指的度数.
使用测倾器测量倾斜角的步骤如下:
(1)把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
(2)转动度盘,使度盘的直径对准目标,记下此时铅垂线所指的度数.
测倾器测量倾斜角的原理:
如图②③所示,分别表示用测倾器测量观测目标P的仰角和俯角,铅垂线指的度数分别为α,β,由“同角的余角相等”知观测目标P的仰角和俯角分别为α,β.所以在用测倾器测量倾斜角时,铅垂线所指的度数即为所测的仰角或俯角的度数.
2.利用三角函数测高
测量物体的高度也是三角函数的实际应用,分为两种情况:
(1)测量底部可以到达的物体的高度,此种情况类似于“三角函数的应用”中的单直角三角形问题.
(2)测量底部不可以到达的物体的高度,此种情况类似于“三角函数的应用”中的双直角三角形问题中的情形,具体步骤如下:
温馨提示
为了提高测量的准确度,同学们可以多次测量,取平均值如果几次测量的误差较大,可能是以下原因所致:
(1)仪器没有放平;
(2)风吹抖动;
(3)测量点的距离太近,角度差别不明显;
(4)测量点与被测物体的底端所在的点不在同一条直线上等为减少误差,要尽可能减少客观因素带来的影响,并且要养成认真细致的学习态度.
例 位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.
(2)∵“景点简介”显示,观星台的高度为12.6m,
∴本次测量结果的误差为12.6-12.3=0.3m.
减小误差的合理化建议:
为了减小误差可以通过多次测量取平均值的方法(答案不唯一).
经典例题
题型一 三角函数测高的应用
方法归纳
此题的解答主要分为两步:
第一步是发现Rt△AEC与Rt△BEC是具有公共直角边的双直角三角形,通过线段间的和差关系或锐角三角函数列方程可求得公共直角边;
第二步是解Rt△DAE.通过这两步,问题便转化为我们熟知的问题,从而顺利获解.
题型二 三角函数测距离的应用
方法归纳
解答此类题的关键是添加辅助线,构造直角三角形此题的解答主要分为两步,一是添加辅助线CM,构造具有公共直角边的双直角三角形,通过线段的和差关系列方程求得公共直角边;第二步是添加辅助线DN,构造单直角三角形,进而解决问题.
6 利用三角函数测高
知识点 利用三角函数测高
1.测量倾斜角
测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成,如图①所示.
使用测倾器测量倾斜角的步骤如下:
(1)把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
(2)转动度盘,使度盘的直径对准目标,记下此时铅垂线所指的度数.
使用测倾器测量倾斜角的步骤如下:
(1)把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
(2)转动度盘,使度盘的直径对准目标,记下此时铅垂线所指的度数.
测倾器测量倾斜角的原理:
如图②③所示,分别表示用测倾器测量观测目标P的仰角和俯角,铅垂线指的度数分别为α,β,由“同角的余角相等”知观测目标P的仰角和俯角分别为α,β.所以在用测倾器测量倾斜角时,铅垂线所指的度数即为所测的仰角或俯角的度数.
2.利用三角函数测高
测量物体的高度也是三角函数的实际应用,分为两种情况:
(1)测量底部可以到达的物体的高度,此种情况类似于“三角函数的应用”中的单直角三角形问题.
(2)测量底部不可以到达的物体的高度,此种情况类似于“三角函数的应用”中的双直角三角形问题中的情形,具体步骤如下:
温馨提示
为了提高测量的准确度,同学们可以多次测量,取平均值如果几次测量的误差较大,可能是以下原因所致:
(1)仪器没有放平;
(2)风吹抖动;
(3)测量点的距离太近,角度差别不明显;
(4)测量点与被测物体的底端所在的点不在同一条直线上等为减少误差,要尽可能减少客观因素带来的影响,并且要养成认真细致的学习态度.
例 位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.
(2)∵“景点简介”显示,观星台的高度为12.6m,
∴本次测量结果的误差为12.6-12.3=0.3m.
减小误差的合理化建议:
为了减小误差可以通过多次测量取平均值的方法(答案不唯一).
经典例题
题型一 三角函数测高的应用
方法归纳
此题的解答主要分为两步:
第一步是发现Rt△AEC与Rt△BEC是具有公共直角边的双直角三角形,通过线段间的和差关系或锐角三角函数列方程可求得公共直角边;
第二步是解Rt△DAE.通过这两步,问题便转化为我们熟知的问题,从而顺利获解.
题型二 三角函数测距离的应用
方法归纳
解答此类题的关键是添加辅助线,构造直角三角形此题的解答主要分为两步,一是添加辅助线CM,构造具有公共直角边的双直角三角形,通过线段的和差关系列方程求得公共直角边;第二步是添加辅助线DN,构造单直角三角形,进而解决问题.
