6.1.3 相等向量与共线向量-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 6.1.3 相等向量与共线向量-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 122.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 13:30:05 | ||
图片预览




文档简介
相等向量与共线向量练习
一、单选题
下列说法中错误的是(? ? )
A. 零向量没有方向 B. 零向量与任何向量平行
C. 零向量的长度为零 D. 零向量的方向是任意的
已知向量AB=a+3b,BC=5a+3b,CD=?3a+3b,则(??? )
A. A,B,C三点共线 B. A,B,D三点共线
C. A,C,D三点共线 D. B,C,D三点共线
下列说法正确的是
A. a//b,b?//c,则a//c
B. 起点相同的两个非零向量不平行
C. 若∣a+b∣=∣a∣+∣b∣,则a与b必共线
D. 若a//b,则a与b的方向相同或相反
设a,b是非零向量,则“a,b共线”是“|a+b|=|a|+|b|”的(????)
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
若|AB|=|AD|且BA=CD,则四边形ABCD的形状为(? ? ? )
A. 正方形 B. 矩形 C. 菱形 D. 等腰梯形
在△ABC中,D,E,F分别为AB,BC,CA的中点,则DE+FC等于??? (? ? ? )
A. AB B. BC C. AC D. AE
如图,在等腰梯形ABCD中,对角线AC与BD交于点P,点E,F分别在两腰AD,BC上,EF过点P,且EF//AB,则下列等式中成立的是(? ? ? ?)
A. AD=BC
B. AC=BD
C. PE=PF
D. EP=PF
已知e1≠0,a=e1+λe2(λ∈R),b=2e1,则a与b共线的条件为(? ? )
A. λ=0 B. e2=0
C. e1//e2 D. e1//e2或λ=0
给出下列命题:①零向量的长度为零,方向是任意的;②若a,b都是单位向量,则a=b;③向量AB与BA相等.则所有正确命题的序号是(????)
A. ① B. ③ C. ①③ D. ①②
如图在梯形ABCD中,BC=2AD,DE=EC,设BA=a,BC=b,则BE=??? (??? )
A. 12a+14b
B. 13a+56b
C. 23a+23b
D. 12a+34b
如图,在平行四边形ABCD中,下列结论中错误的是(? ?)
A. AB=DC B. AD+AB=AC
C. AB?AD=BD D. AD+CB=0
A,B,C是平面上不共线的三点,O是的重心,动点P满足OP=13(12OA+12OB+2OC),则点P一定为(? ? ? ? )
A. AB边中线的中点 B. AB边中线的三等分点(非重心)
C. BC边中线的中点 D. AB边的中点
若向量a,b不共线,且a+mb与(b?2a)共线,则实数m的值为(????)
A. 12 B. ?12 C. 2 D. ?2
二、单空题
若e1,e2是夹角为60°的两个单位向量,向量a=2e1+e2,则|a|=______.
给出以下五个条件:①a=b;②|a|=|b|;③a与b的方向相反;④|a|=0或|b|=0;⑤a与b都是单位向量.其中能使a//b成立的是_________.(填写所有正确的序号)
已知平面向量a=(1,2),b=(?2,m),且a//b,则2a+3b=? ? ? ?.
已知向量a,b不共线,若向量ka+b与a+2b平行,则实数k=______.
已知m,n均为正数,,,且,则的最小值为____.
三、解答题
如图所示,O为正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,根据图中所标出的向量回答下列问题.
(1)分别写出与AO,BO相等的向量;
(2)写出与AO共线的向量;
(3)写出与AO模相等的向量
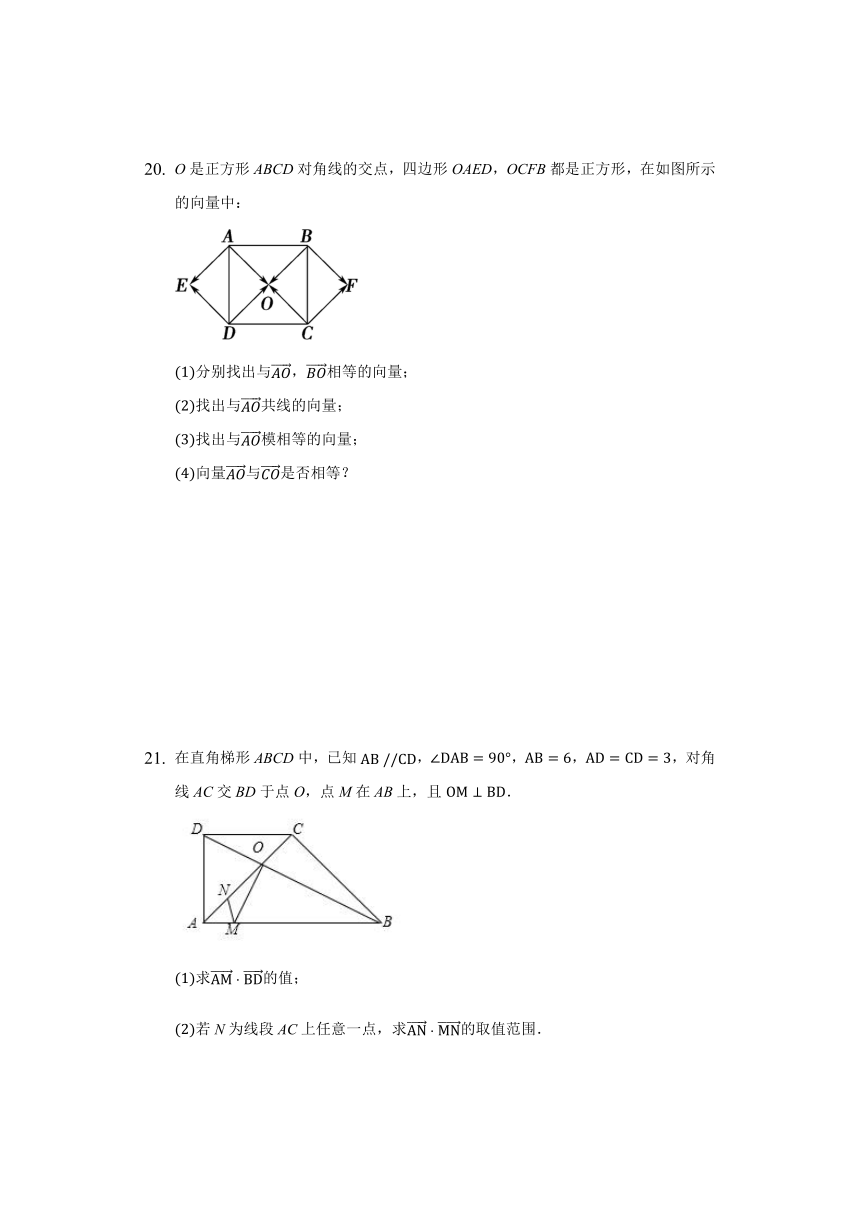
O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在如图所示的向量中:
(1)分别找出与AO,BO相等的向量;
(2)找出与AO共线的向量;
(3)找出与AO模相等的向量;
(4)向量AO与CO是否相等?
在直角梯形ABCD中,已知AB?//CD,∠DAB=90°,AB=6,AD=CD=3,对角线AC交BD于点O,点M在AB上,且OM⊥BD.
(1)求AM?BD的值;
(2)若N为线段AC上任意一点,求AN?MN的取值范围.
已知点O(0,0),A(2,1),B(3,4),且OM=OA+tAB.
??? (1)若点M在第四象限,求实数t的取值范围;
??? (2)四边形OABM能否为平行四边形?若能,求出相应t的值;若不能,请说明理由.
答案和解析
1.【答案】A
【解答】
解:据零向量的定义:模为零的向量为零向量判断出C对,
对零向量的规定:零向量的方向是任意的;零向量与任何向量平行,
判断出B,D对,判断出A错,
2.【答案】B
【解答】解:∵BD=BC+CD=2a+6b=2(a+3b)=2AB,
∴BD,AB共线,且有公共点B,
∴A,B,D三点共线.
3.【答案】C
【解答】
解:当b=0时,a//b,b//c,但a//c不一定成立,A错;
起点相同的两个非零向量当他们方向相同或相反时,一定平行,B错;
若∣a+b∣=∣a∣+∣b∣,即a与b必共线,C对;
若a//b,若其中有一个为零向量,不一定成立,D错.
4.【答案】B
【解答】
解:“|a+b|=|a|+|b|”?“a,b共线”,反之不成立,例如a=?b≠0.
∴a,b是非零向量,则“a,b共线”是“|a+b|=|a|+|b|”的必要不充分条件.
5.【答案】C
【解答】
解:四边形ABCD中,
∵BA=CD,
∴BA//CD,且BA=CD,
∴四边形ABCD是平行四边形;
又|AB|=|AD|,
∴平行四边形ABCD是菱形;
6.【答案】C
【解答】解:∵D,E,F分别为AB,BC,AC的中点,
∴DE//AF且DE=AF,
∴DE =AF,
∴DE +FC =AF +FC =AC .
7.【答案】D
【解答】
解:根据相等向量的定义,
A中,AD与BC的方向不同,故A错误;
B中,AC与BD的方向不同,故B错误;
C中,PE与PF的方向相反,故C错误;
D中,EP与PF的方向相同,且长度都等于线段EF长度的一半,故D正确.
8.【答案】D
【解答】解:若a,b共线,则存在m,使a=mb,即e1+λe2=2me1,
所以当a,b共线时,有λ=0或e1//e2.
9.【答案】A
【解答】
解:根据零向量的定义可知①正确;
根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;
向量AB与BA互为相反向量,故③错误.
10.【答案】D
【解答】
解:取BC中点F,连接FA,
因为在梯形ABCD中,BC=2AD,所以四边形ADCF是平行四边形,
所以FA//CD,FA=CD,
则BE=BC+CE=BC+12CD=BC+12FA?
=BC+12(BA?BF)=BC+12(BA?12BC)?
=12BA+34BC=12a+34b.
11.【答案】C
【解答】
解:因为AB=DC,
所以A正确;
因为AD+AB=AC,
所以B正确;
因为AB?AD=DB
所以C错;
因为AD与CB为相反向量,
所以D正确.
12.【答案】B
【解答】
解:如图所示:设AB,BC,AC的中点分别是是E,D,F.
∵O是三角形ABC的重心,
∵OP=13(12OA+12OB+2OC)=13(OE+2OC),
∵2EO=OC,
∴OP=13×(4EO+OE)=EO
∴P在AB边的中线上,是中线的三等分点,不是重心.
13.【答案】B
【解析】解:∵a,b不共线,
∴b?2a≠0,
又a+mb与b?2a共线,
∴存在实数k,使a+mb=k(b?2a),
∴?2k=1m=k,解得m=?12.
14.【答案】7
【解答】
解:e1?e2=12,e12=e22=1,
∴a2=(2e1+e2)2
=4e12+4e1?e2+e22=4+2+1=7,
∴|a|=7.
故答案为7.
15.【答案】①③④
【解答】解:共线向量指的是方向相同或相反的向量,它只涉及方向,不涉及大小.显然只有①③④满足题意.
16.【答案】(?4,?8)
【解答】
解:∵a//b,∴??21=m2,
m=?4,b=(?2,?4),
2a+3b=(2,4)+(?6,?12)=(?4,?8).
故答案为(?4,?8).
17.【答案】12
【解析】解:∵向量ka+b与a+2b平行,
∴存在实数λ使得:ka+b=λ(a+2b),
∵向量a,b不共线,∴k=λ1=2λ,
解得k=12.
故答案为:12.
18.【答案】4
【解答】
解:∵m,n均为正数,a=(1,m),b=(2,1?n),且a//b,
∴1?n=2m,故2m+n=1.
∴1m+mn=2m+nm+mn=2+nm+mn≥2+2nm·mn=4,当且仅当m=n?时等号成立,
故1m+mn的最小值为4.
故答案为:4.
19.【答案】解:(1)由正方形的性质可知:AO=BF,BO=AE
??????? (2)与AO共线的向量是CO,BF,DE
??????? (3)因为AO=1,所以与AO模相等的向量CO,BF,DE,AE,BO,DO,CF.
20.【答案】解:(1)AO=BF?,BO=AE
(2)与AO?共线的向量有:BF?,CO?,DE?.
(3)与AO?模相等的向量有:CO?,DO?,BO?,BF?,CF?,AE?,DE?.
(4)向量AO?与CO?不相等,因为它们的方向不相同.
21.【答案】解:(1)因为∠DAB=90°,
所以以A为坐标原点,AB、AD分别为x、y轴,建立平面直角坐标系如下图:
因为AB?//CD,AB=6,AD=CD=3,
所以A0,0,B6,0,C3,3,D0,3.
又因为对角线AC交BD于点O,
所以由AO=tAC得AO=3t,3t,即O3t,3t,
因此DO=3t,3t?3,DB=6,?3,
而DO//DB,所以?3×3t?6×3t?3=0,解得t=23,
因此O2,2.
又因为点M在AB上,所以设Mm,0,
因此OM=m?2,?2,BD=?6,3,
而OM⊥BD,所以OM·BD=?6m?2?6=0,
解得m=1,即M1,0,
因此AM=1,0,而BD=?6,3,
所以AM?BD=?6,
即AM?BD的值为?6;
(2)因为N为线段AC上任意一点,
所以由(1)知:可设Nn,n0?n?3(包括端点),
因此AN=n,n,MN=n?1,n,
所以AN?MN=nn?1+n2=2n2?n.
因为函数y=2n2?n的图象开口上,对称轴为n=14,
而0?n?3,
所以函数y=2n2?n的值域为?18,15,
即AN?MN的取值范围是?18,15.
22.【答案】解(1)∵?OM=OA+tAB=(2,?1)+t(1?,?3)=(2+t?,?1+3t)?,
∴点M?(2+t?,?1+3t).
∵点M在第四象限,∴2+t>01+3t<0,解得?2所以实数t的取值范围为(?2,?13).
(2)不能.
若OABM为平行四边形,则OA=MB,
∵OA=(2,1),MB=(1?t,3?3t),
∴2=1?t1=3?3t,此方程组无解,
所以OABM不能是平行四边形.
一、单选题
下列说法中错误的是(? ? )
A. 零向量没有方向 B. 零向量与任何向量平行
C. 零向量的长度为零 D. 零向量的方向是任意的
已知向量AB=a+3b,BC=5a+3b,CD=?3a+3b,则(??? )
A. A,B,C三点共线 B. A,B,D三点共线
C. A,C,D三点共线 D. B,C,D三点共线
下列说法正确的是
A. a//b,b?//c,则a//c
B. 起点相同的两个非零向量不平行
C. 若∣a+b∣=∣a∣+∣b∣,则a与b必共线
D. 若a//b,则a与b的方向相同或相反
设a,b是非零向量,则“a,b共线”是“|a+b|=|a|+|b|”的(????)
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
若|AB|=|AD|且BA=CD,则四边形ABCD的形状为(? ? ? )
A. 正方形 B. 矩形 C. 菱形 D. 等腰梯形
在△ABC中,D,E,F分别为AB,BC,CA的中点,则DE+FC等于??? (? ? ? )
A. AB B. BC C. AC D. AE
如图,在等腰梯形ABCD中,对角线AC与BD交于点P,点E,F分别在两腰AD,BC上,EF过点P,且EF//AB,则下列等式中成立的是(? ? ? ?)
A. AD=BC
B. AC=BD
C. PE=PF
D. EP=PF
已知e1≠0,a=e1+λe2(λ∈R),b=2e1,则a与b共线的条件为(? ? )
A. λ=0 B. e2=0
C. e1//e2 D. e1//e2或λ=0
给出下列命题:①零向量的长度为零,方向是任意的;②若a,b都是单位向量,则a=b;③向量AB与BA相等.则所有正确命题的序号是(????)
A. ① B. ③ C. ①③ D. ①②
如图在梯形ABCD中,BC=2AD,DE=EC,设BA=a,BC=b,则BE=??? (??? )
A. 12a+14b
B. 13a+56b
C. 23a+23b
D. 12a+34b
如图,在平行四边形ABCD中,下列结论中错误的是(? ?)
A. AB=DC B. AD+AB=AC
C. AB?AD=BD D. AD+CB=0
A,B,C是平面上不共线的三点,O是的重心,动点P满足OP=13(12OA+12OB+2OC),则点P一定为(? ? ? ? )
A. AB边中线的中点 B. AB边中线的三等分点(非重心)
C. BC边中线的中点 D. AB边的中点
若向量a,b不共线,且a+mb与(b?2a)共线,则实数m的值为(????)
A. 12 B. ?12 C. 2 D. ?2
二、单空题
若e1,e2是夹角为60°的两个单位向量,向量a=2e1+e2,则|a|=______.
给出以下五个条件:①a=b;②|a|=|b|;③a与b的方向相反;④|a|=0或|b|=0;⑤a与b都是单位向量.其中能使a//b成立的是_________.(填写所有正确的序号)
已知平面向量a=(1,2),b=(?2,m),且a//b,则2a+3b=? ? ? ?.
已知向量a,b不共线,若向量ka+b与a+2b平行,则实数k=______.
已知m,n均为正数,,,且,则的最小值为____.
三、解答题
如图所示,O为正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,根据图中所标出的向量回答下列问题.
(1)分别写出与AO,BO相等的向量;
(2)写出与AO共线的向量;
(3)写出与AO模相等的向量
O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在如图所示的向量中:
(1)分别找出与AO,BO相等的向量;
(2)找出与AO共线的向量;
(3)找出与AO模相等的向量;
(4)向量AO与CO是否相等?
在直角梯形ABCD中,已知AB?//CD,∠DAB=90°,AB=6,AD=CD=3,对角线AC交BD于点O,点M在AB上,且OM⊥BD.
(1)求AM?BD的值;
(2)若N为线段AC上任意一点,求AN?MN的取值范围.
已知点O(0,0),A(2,1),B(3,4),且OM=OA+tAB.
??? (1)若点M在第四象限,求实数t的取值范围;
??? (2)四边形OABM能否为平行四边形?若能,求出相应t的值;若不能,请说明理由.
答案和解析
1.【答案】A
【解答】
解:据零向量的定义:模为零的向量为零向量判断出C对,
对零向量的规定:零向量的方向是任意的;零向量与任何向量平行,
判断出B,D对,判断出A错,
2.【答案】B
【解答】解:∵BD=BC+CD=2a+6b=2(a+3b)=2AB,
∴BD,AB共线,且有公共点B,
∴A,B,D三点共线.
3.【答案】C
【解答】
解:当b=0时,a//b,b//c,但a//c不一定成立,A错;
起点相同的两个非零向量当他们方向相同或相反时,一定平行,B错;
若∣a+b∣=∣a∣+∣b∣,即a与b必共线,C对;
若a//b,若其中有一个为零向量,不一定成立,D错.
4.【答案】B
【解答】
解:“|a+b|=|a|+|b|”?“a,b共线”,反之不成立,例如a=?b≠0.
∴a,b是非零向量,则“a,b共线”是“|a+b|=|a|+|b|”的必要不充分条件.
5.【答案】C
【解答】
解:四边形ABCD中,
∵BA=CD,
∴BA//CD,且BA=CD,
∴四边形ABCD是平行四边形;
又|AB|=|AD|,
∴平行四边形ABCD是菱形;
6.【答案】C
【解答】解:∵D,E,F分别为AB,BC,AC的中点,
∴DE//AF且DE=AF,
∴DE =AF,
∴DE +FC =AF +FC =AC .
7.【答案】D
【解答】
解:根据相等向量的定义,
A中,AD与BC的方向不同,故A错误;
B中,AC与BD的方向不同,故B错误;
C中,PE与PF的方向相反,故C错误;
D中,EP与PF的方向相同,且长度都等于线段EF长度的一半,故D正确.
8.【答案】D
【解答】解:若a,b共线,则存在m,使a=mb,即e1+λe2=2me1,
所以当a,b共线时,有λ=0或e1//e2.
9.【答案】A
【解答】
解:根据零向量的定义可知①正确;
根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;
向量AB与BA互为相反向量,故③错误.
10.【答案】D
【解答】
解:取BC中点F,连接FA,
因为在梯形ABCD中,BC=2AD,所以四边形ADCF是平行四边形,
所以FA//CD,FA=CD,
则BE=BC+CE=BC+12CD=BC+12FA?
=BC+12(BA?BF)=BC+12(BA?12BC)?
=12BA+34BC=12a+34b.
11.【答案】C
【解答】
解:因为AB=DC,
所以A正确;
因为AD+AB=AC,
所以B正确;
因为AB?AD=DB
所以C错;
因为AD与CB为相反向量,
所以D正确.
12.【答案】B
【解答】
解:如图所示:设AB,BC,AC的中点分别是是E,D,F.
∵O是三角形ABC的重心,
∵OP=13(12OA+12OB+2OC)=13(OE+2OC),
∵2EO=OC,
∴OP=13×(4EO+OE)=EO
∴P在AB边的中线上,是中线的三等分点,不是重心.
13.【答案】B
【解析】解:∵a,b不共线,
∴b?2a≠0,
又a+mb与b?2a共线,
∴存在实数k,使a+mb=k(b?2a),
∴?2k=1m=k,解得m=?12.
14.【答案】7
【解答】
解:e1?e2=12,e12=e22=1,
∴a2=(2e1+e2)2
=4e12+4e1?e2+e22=4+2+1=7,
∴|a|=7.
故答案为7.
15.【答案】①③④
【解答】解:共线向量指的是方向相同或相反的向量,它只涉及方向,不涉及大小.显然只有①③④满足题意.
16.【答案】(?4,?8)
【解答】
解:∵a//b,∴??21=m2,
m=?4,b=(?2,?4),
2a+3b=(2,4)+(?6,?12)=(?4,?8).
故答案为(?4,?8).
17.【答案】12
【解析】解:∵向量ka+b与a+2b平行,
∴存在实数λ使得:ka+b=λ(a+2b),
∵向量a,b不共线,∴k=λ1=2λ,
解得k=12.
故答案为:12.
18.【答案】4
【解答】
解:∵m,n均为正数,a=(1,m),b=(2,1?n),且a//b,
∴1?n=2m,故2m+n=1.
∴1m+mn=2m+nm+mn=2+nm+mn≥2+2nm·mn=4,当且仅当m=n?时等号成立,
故1m+mn的最小值为4.
故答案为:4.
19.【答案】解:(1)由正方形的性质可知:AO=BF,BO=AE
??????? (2)与AO共线的向量是CO,BF,DE
??????? (3)因为AO=1,所以与AO模相等的向量CO,BF,DE,AE,BO,DO,CF.
20.【答案】解:(1)AO=BF?,BO=AE
(2)与AO?共线的向量有:BF?,CO?,DE?.
(3)与AO?模相等的向量有:CO?,DO?,BO?,BF?,CF?,AE?,DE?.
(4)向量AO?与CO?不相等,因为它们的方向不相同.
21.【答案】解:(1)因为∠DAB=90°,
所以以A为坐标原点,AB、AD分别为x、y轴,建立平面直角坐标系如下图:
因为AB?//CD,AB=6,AD=CD=3,
所以A0,0,B6,0,C3,3,D0,3.
又因为对角线AC交BD于点O,
所以由AO=tAC得AO=3t,3t,即O3t,3t,
因此DO=3t,3t?3,DB=6,?3,
而DO//DB,所以?3×3t?6×3t?3=0,解得t=23,
因此O2,2.
又因为点M在AB上,所以设Mm,0,
因此OM=m?2,?2,BD=?6,3,
而OM⊥BD,所以OM·BD=?6m?2?6=0,
解得m=1,即M1,0,
因此AM=1,0,而BD=?6,3,
所以AM?BD=?6,
即AM?BD的值为?6;
(2)因为N为线段AC上任意一点,
所以由(1)知:可设Nn,n0?n?3(包括端点),
因此AN=n,n,MN=n?1,n,
所以AN?MN=nn?1+n2=2n2?n.
因为函数y=2n2?n的图象开口上,对称轴为n=14,
而0?n?3,
所以函数y=2n2?n的值域为?18,15,
即AN?MN的取值范围是?18,15.
22.【答案】解(1)∵?OM=OA+tAB=(2,?1)+t(1?,?3)=(2+t?,?1+3t)?,
∴点M?(2+t?,?1+3t).
∵点M在第四象限,∴2+t>01+3t<0,解得?2
(2)不能.
若OABM为平行四边形,则OA=MB,
∵OA=(2,1),MB=(1?t,3?3t),
∴2=1?t1=3?3t,此方程组无解,
所以OABM不能是平行四边形.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
