北师大七年级数学下册第二章单元测试

北师大七年级数学下册第二章《平行线与相交线》单元测试
一、判断题
1．两直线相交，有公共顶点的角是对顶角． （ ）
2．同一平面内不相交的两条线段必平行． （ ）
3．一个钝角的补角比它的余角大90 ． （ ）
4．平面内两条直线被第三条直线所截，如果内错角相等，则同位角也相等． （ ）
5．如果一个角等于它的补角，那么这个角一定是直角． （ ）
6．如果m∥l，n∥l，那么根据等量代换，有m∥n． （ ）
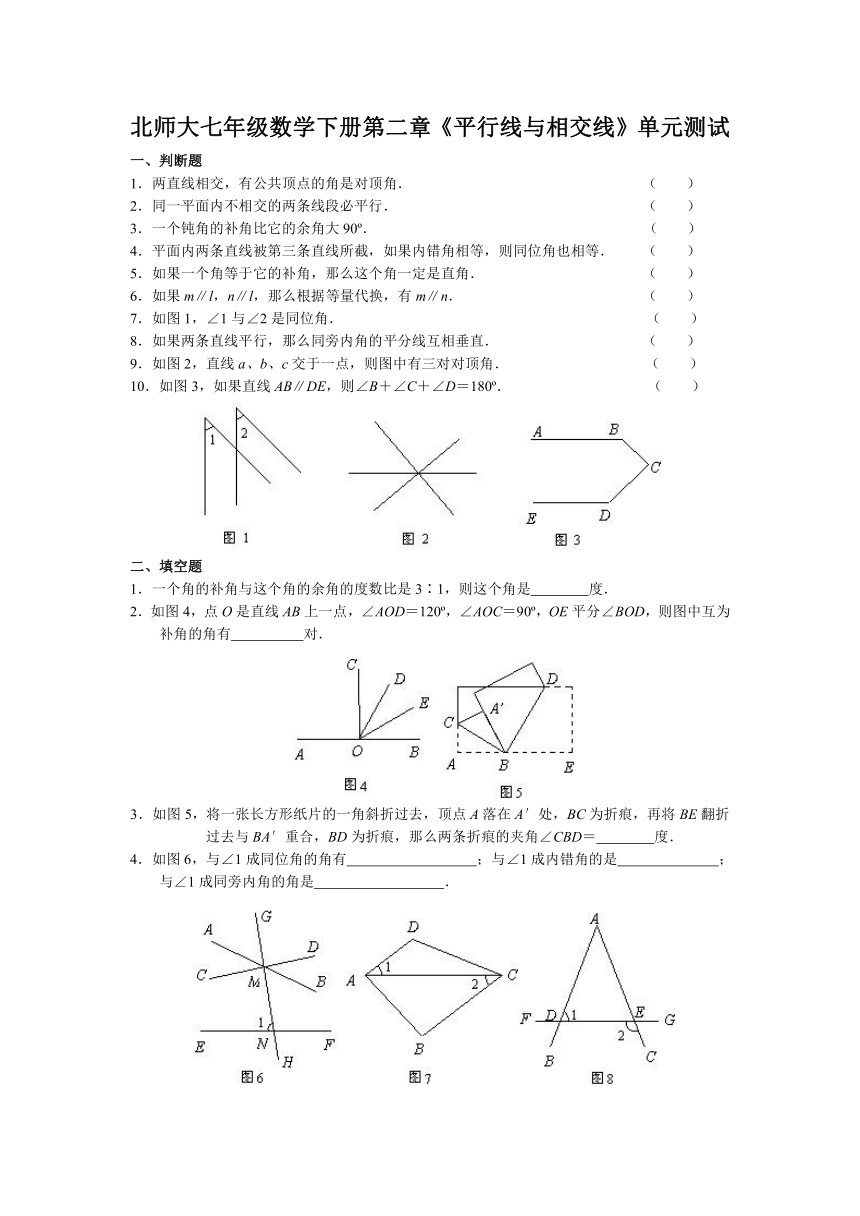
7．如图1，∠1与∠2是同位角． （ ）
8．如果两条直线平行，那么同旁内角的平分线互相垂直． （ ）
9．如图2，直线a、b、c交于一点，则图中有三对对顶角． （ ）
10．如图3，如果直线AB∥DE，则∠B＋∠C＋∠D＝180 ． （ ）
二、填空题
1．一个角的补角与这个角的余角的度数比是3∶1，则这个角是 度．
2．如图4，点O是直线AB上一点，∠AOD＝120 ，∠AOC＝90 ，OE平分∠BOD，则图中互为补角的角有 对．
3．如图5，将一张长方形纸片的一角斜折过去，顶点A落在A′处，BC为折痕，再将BE翻折过去与BA′重合，BD为折痕，那么两条折痕的夹角∠CBD＝ 度．
4．如图6，与∠1成同位角的角有 ；与∠1成内错角的是 ；与∠1成同旁内角的角是 ．
5．如图7，∠1＝∠2，∠DAB＝85 ，则∠B＝ 度．
6．如图8，已知∠1＋∠2＝180 ，则图中与∠1相等的角共有 个．
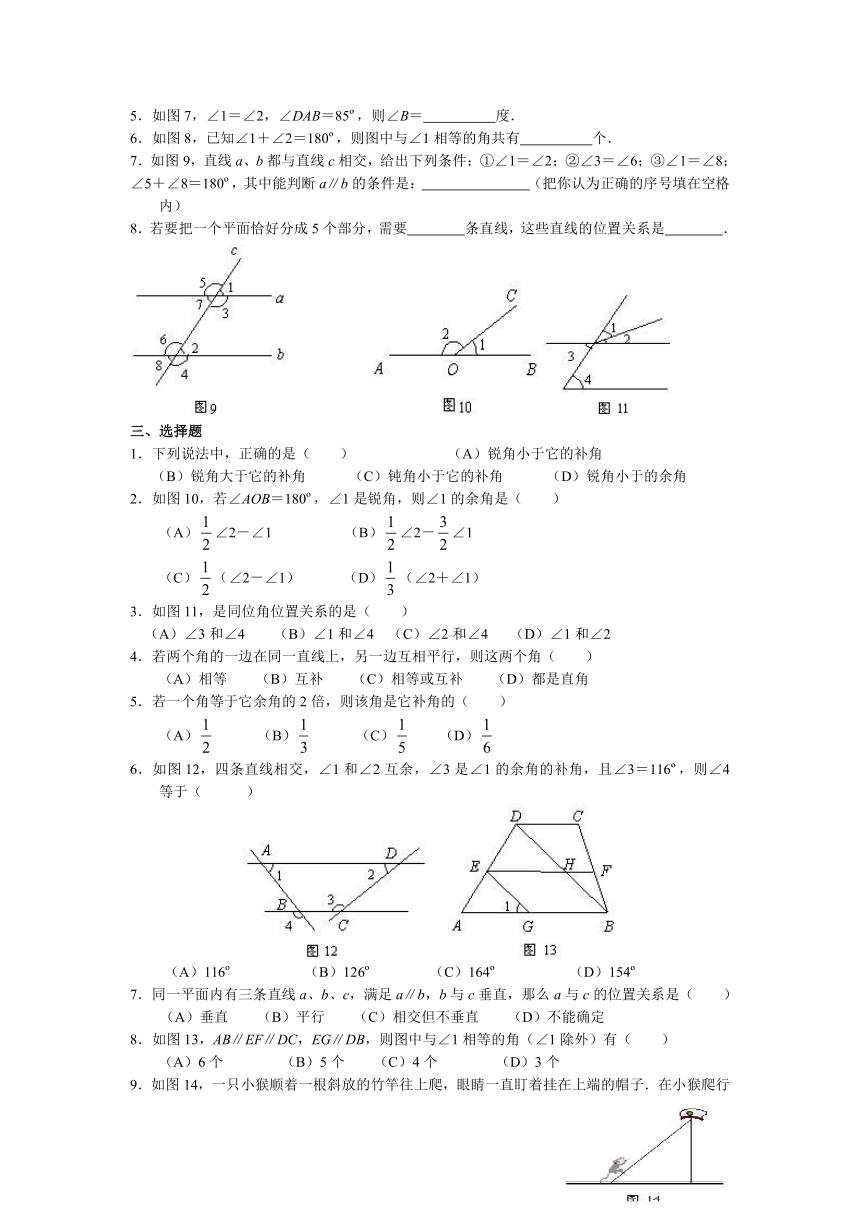
7．如图9，直线a、b都与直线c相交，给出下列条件：①∠1＝∠2；②∠3＝∠6；③∠1＝∠8；
∠5＋∠8＝180 ，其中能判断a∥b的条件是： （把你认为正确的序号填在空格内）
8．若要把一个平面恰好分成5个部分，需要 条直线，这些直线的位置关系是 ．
三、选择题
1．下列说法中，正确的是（ ） （A）锐角小于它的补角
（B）锐角大于它的补角 （C）钝角小于它的补角 （D）锐角小于的余角
2．如图10，若∠AOB＝180 ，∠1是锐角，则∠1的余角是（ ）
（A）∠2－∠1 （B）∠2－∠1
（C）（∠2－∠1） （D）（∠2＋∠1）
3．如图11，是同位角位置关系的是（ ）
（A）∠3和∠4 （B）∠1和∠4 （C）∠2和∠4 （D）∠1和∠2
4．若两个角的一边在同一直线上，另一边互相平行，则这两个角（ ）
（A）相等 （B）互补 （C）相等或互补 （D）都是直角
5．若一个角等于它余角的2倍，则该角是它补角的（ ）
（A） （B） （C） （D）
6．如图12，四条直线相交，∠1和∠2互余，∠3是∠1的余角的补角，且∠3＝116 ，则∠4等于（ ）
（A）116 （B）126 （C）164 （D）154
7．同一平面内有三条直线a、b、c，满足a∥b，b与c垂直，那么a与c的位置关系是（ ）
（A）垂直 （B）平行 （C）相交但不垂直 （D）不能确定
8．如图13，AB∥EF∥DC，EG∥DB，则图中与∠1相等的角（∠1除外）有（ ）
（A）6个 （B）5个 （C）4个 （D）3个
9．如图14，一只小猴顺着一根斜放的竹竿往上爬，眼睛一直盯着挂在上端的帽子．在小猴爬行的过程中，视线与水平方向所成角（ ）
（A）逐渐变大 （B）逐渐变小
（C）没有变化 （D）无法确定
10．下列判断正确的是（ ）
（A）相等的角是对顶角 （B）互为补角的两个角一定是一个锐角和一个钝角
（C）内错角相等 （D）等角的补角相等
四、解答下列各题
1．一个角的补角与它余角的2倍的差是平角的，求这个角的度数．
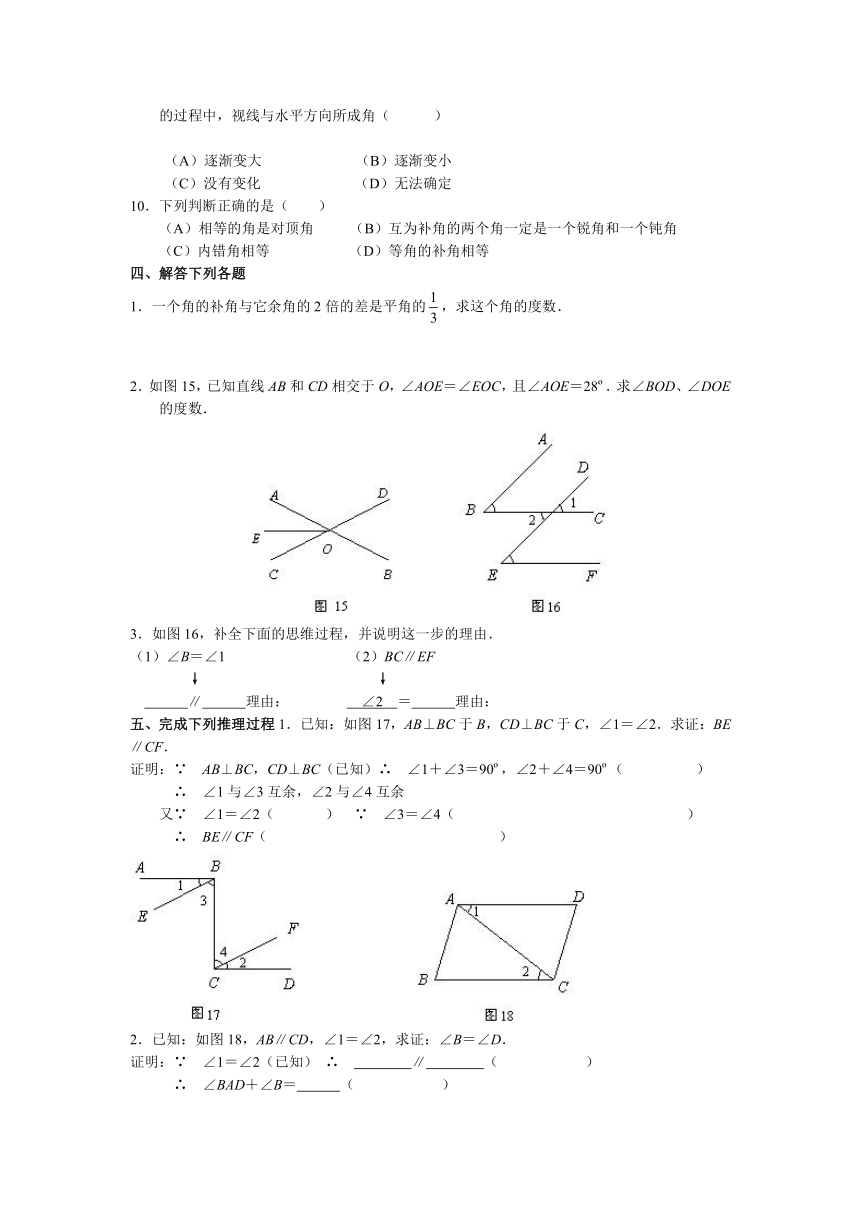
2．如图15，已知直线AB和CD相交于O，∠AOE＝∠EOC，且∠AOE＝28 ．求∠BOD、∠DOE的度数．
3．如图16，补全下面的思维过程，并说明这一步的理由．
（1）∠B＝∠1 （2）BC∥EF
↓ ↓
∥ 理由： ∠2 ＝ 理由：
五、完成下列推理过程1．已知：如图17，AB⊥BC于B，CD⊥BC于C，∠1＝∠2．求证：BE∥CF．
证明：∵ AB⊥BC，CD⊥BC（已知）∴ ∠1＋∠3＝90 ，∠2＋∠4＝90 （ ）
∴ ∠1与∠3互余，∠2与∠4互余
又∵ ∠1＝∠2（ ） ∵ ∠3＝∠4（ ）
∴ BE∥CF（ ）
2．已知：如图18，AB∥CD，∠1＝∠2，求证：∠B＝∠D．
证明：∵ ∠1＝∠2（已知） ∴ ∥ （ ）
∴ ∠BAD＋∠B＝ （ ）
又∵ AB∥CD（已知） ∴ ＋ ＝180 （ ）
∴ ∠B＝∠D（ ）
六、作图题如图19，已知∠BAC及BA上一点P，求作直线MN，使MN经过点P，且MN∥AC．
（要求：使用尺规正确作图，保留作图痕迹）
七、计算与说理1．已知：如图20，∠ABC＝50 ，∠ACB＝60 ，∠ABC、∠ACB的平分线交于点O，过点O作EF∥BC交AB于E，交AC于F．求∠BOC的度数．
2．如图21，AB∥DE，∠1＝∠ACB，∠CAB＝∠BAD，试说明AD∥BC．
绝密★档案E
第二章平行线与相交线单元测试(2)
一、填空(7×3)
1．如图，已知CB＝4，DB＝7，D是AC的中点，
则AC＝_________ .
2．时钟的时针和分针在2时30分时，所成的角度是_____度.
3．如图1，CB⊥AB，∠CBA与∠CBD的度数比是5:1，则∠DBA＝________度，∠CBD
的补角是_________度.
＜图4＞ ＜图5＞ ＜图6＞
＜图1＞ ＜图2＞ ＜图3＞
4．如图2，AC⊥BC，CD⊥AB，∠A的余角有______个，和∠A相等的角有_______个.
5．如图3，当∠1＝∠_____时，AB∥CD；当∠D＋∠_____＝180°时，AB∥CD；当∠B
＝∠_____时，AB∥CD.
6．若两个角的两边分别平行，而一个角30°，则另一角的度数是____________________.
7、命题“同角的补角相等”改写成“如果……， 那么……”的形式可写成
______________________________.
二、选择题(6×3)
8、命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等。其中假命题有（ ） A、1个 B、2个 C、3个 D、4个
9、．互为余角的两个角之差为35°，则较大角的补角是（ ）
A．117.5° B．112.5° C．125° D．127.5°
10．已知，如图4，AB∥CD，则∠α、∠β、∠γ之间的关系为（ ）
A．∠α＋∠β＋∠γ＝360° B．∠α－∠β＋∠γ＝180°
C．∠α＋∠β－∠γ＝180° D．∠α＋∠β＋∠γ＝180°
＜图4＞ ＜图5＞ ＜图6＞
11．如图5，由A到B的方向是（ ）
A．南偏东30°
B．南偏东60°
C．北偏西30°
D．北偏西60°
12．如图6，∠AOE＝∠BOC，OD平分∠COE，那么图中除∠AOE＝∠BOC外，相等的角共有（ ）
A．1对 B．2对
C．3对 D．4对
13、如图，已知∠1=∠2，∠BAD=∠BCD，则下列结论
(1)AB//CD；(2)AD//BC；(3)∠B=∠D；(4)∠D=∠ACB。
其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个
三、填写理由（3×7）
1、已知：如图、BE//CF，BE、CF分别平分∠ABC和∠BCD
求证：AB//CD
证明：∵BE、平分∠ABC（已知）
∴∠1=∠
∵CF平分∠BCD（ ）
∠2=∠ （ ）
∵BE//CF（已知）
∴∠1=∠2（ ）
∴∠ABC=∠BCD（ ）
即∠ABC=∠BCD
∴AB//CD（ ）
2、如图，已知：∠BCF=∠B+∠F。
求证：AB//EF
证明：经过点C作CD//AB
∴∠BCD=∠B。（ ）
∵∠BCF=∠B+∠F，（已知）
∴∠ （ ）=∠F。（ ）
∴CD//EF。（ ）
∴AB//EF（ ）
3、已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4。
求证：AD∥BE。
证明：∵AB∥CD（已知）
∴∠4=∠ （ ）
∵∠3=∠4（已知）
∴∠3=∠ （ ）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（ ）
即∠ =∠
∴∠3=∠ （ ）
∴AD∥BE（ ）
四、解答题(5×8)
1、若一个角的补角是它的余角的3倍，求这个角的度数
2、已知：如图，AB//CD，BC//DE，∠B=70°，
（1）求∠D的度数。
（2）用尺规在图上作一个角，使=∠D—∠B（不写作法，保留痕迹）
3、已知：BC//EF，∠B=∠E，
求证：AB//DE。
4、如图，已知、BE平分∠ABC，∠CBE=25°，∠BED=25°，∠C=30°，求∠ADE与∠BEC的度数。
5、将两个形状相同的三角板的最长边靠在一起，上下滑动，直角边AB，CD有何位置关系 并证明
6、已知、将一幅三角板的直角顶点重合，
（1）写出与∠COA相等的角，并证明
（2）找出所有互补的角，并证明
附加题（+10）
如图、A1A2∥AnAn-1，=∠+∠，=∠+∠+……∠+∠
判断与的数量关系，并证明
A
B
C
D
1
2
A
C
D
F
B
E
1
2
B
A
E
F
C
D
A
D
B
C
E
F
1
2
3
4
A
B
E
D
C
A
B
E
P
D
C
F
A
B
C
D
E