第4章多项式的运算复习
图片预览

文档简介
第4章多项式的运算复习
教学目标
1 掌握多项式的加减法、乘法运算法则,并能熟练地进行多项式的加减、乘运算。
2掌握同底数的幂的乘法、幂的乘方运算法则并能熟练的进行运算。
教学重点、难点
重点:整式加、减、乘运算法则及应用。
难点:多项式加、减、乘混合运算
教学过程
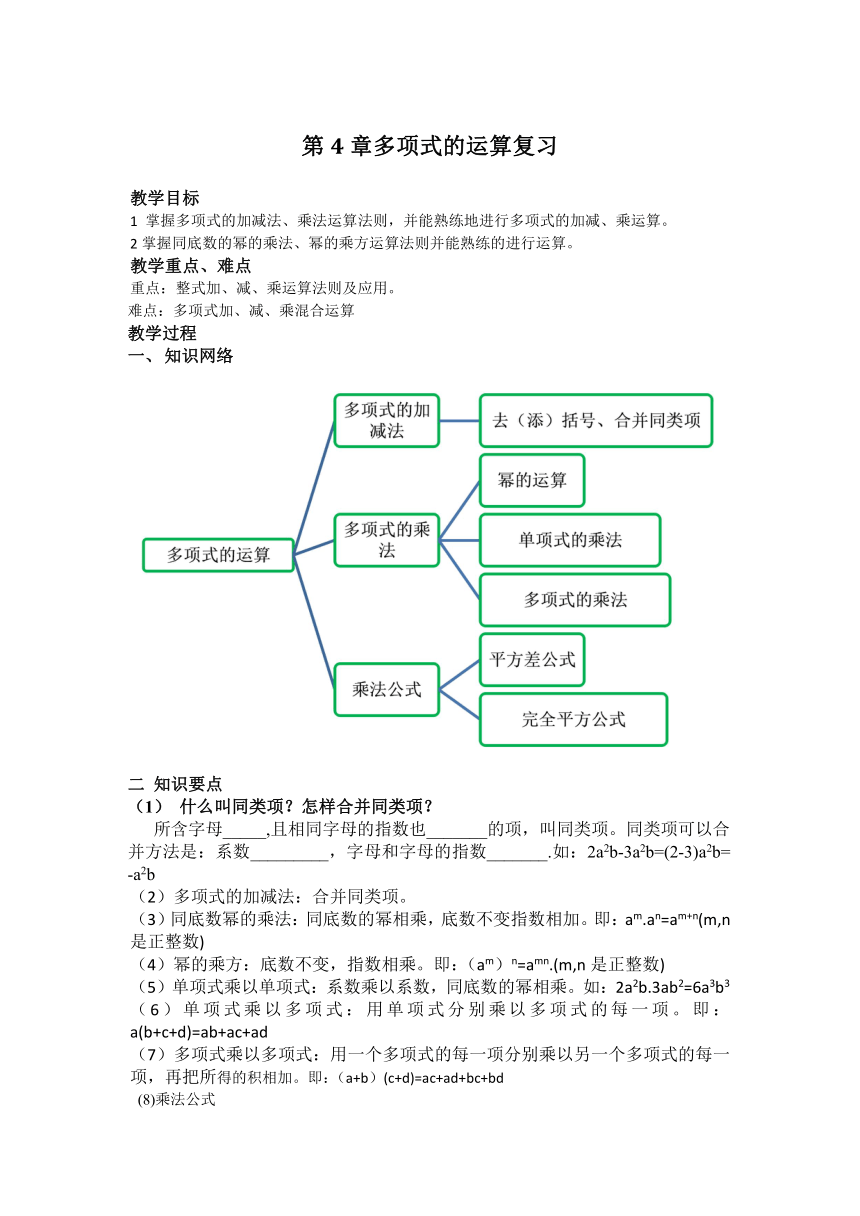
知识网络
二 知识要点
什么叫同类项?怎样合并同类项?
所含字母_____,且相同字母的指数也_______的项,叫同类项。同类项可以合并方法是:系数_________,字母和字母的指数_______.如:2a2b-3a2b=(2-3)a2b= -a2b
(2)多项式的加减法:合并同类项。
(3)同底数幂的乘法:同底数的幂相乘,底数不变指数相加。即:am.an=am+n(m,n是正整数)
(4)幂的乘方:底数不变,指数相乘。即:(am)n=amn.(m,n是正整数)
(5)单项式乘以单项式:系数乘以系数,同底数的幂相乘。如:2a2b.3ab2=6a3b3
(6)单项式乘以多项式:用单项式分别乘以多项式的每一项。即:a(b+c+d)=ab+ac+ad
(7)多项式乘以多项式:用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。即:(a+b)(c+d)=ac+ad+bc+bd
(8)乘法公式
①平方差公式:(a+b)(a-b)=a2-b2
两个数的和乘以这两个数的差,等于这两个数的平方差。
②(a±b)2=a2±2ab+b2
两个数的和或差的平方,等于这两个数的平方和加上(或减去)这两个数的积的二倍。
二 专题训练
1、把握公式特征,灵活运算法则
【例1】有这样一道题:“计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+2x2y-y3)
的值,其中x= ,y=-1.”错抄成了“x= ”,但他计算的结果也是正确的,这是怎么回事呢?
【分析】先化简,由于x的值抄错成它的相反数,所以,化简后的式子含有x的项中,只有x2,而没有x3、x项或者没有含有x的项。
【解】原式=2x3-3x2y-2xy2-x3+2xy2-y3-x3+2x2y-y3=-x2y-2y3
当x=0.5,y=-1时,原式=-0.52×(-1)-2×(-1)3=2.25
当x=-0.5,y=-1时,原式=-(-0.5)2×(-1)-2×(-1)3=2.25
【变式练习】
1、(2010福建泉州)若a、b 是正数,a﹣b=l,ab=2,则a+b=( )
A.﹣3 B.3 C.±3 D.9
【分析】根据(a+b)2=(a﹣b)2+4ab,代值计算,再开平方求解.注意若a、b 是正数,则a+b>0.
【解】:∵(a+b)2=(a﹣b)2+4ab=12+4×2=9,开平方,得a+b=±3,又∵a、b 是正数,
∴a+b>0,∴a+b=3.故选B.
【点评】本题考查了完全平方公式,熟记公式的几个变形公式对解题大有帮助.
2、(2011广东湛江)下列计算正确的是( )
A、a2 a3=a5 B、a+a=a2 C、(a2)3=a5 D、a2(a+1)=a3+1
【分析】:根据同底数幂的乘法法则:底数不变,指数相加,以及合并同类项:只把系数相加,字母及其指数完全不变.积的乘方:等于把积的每一个因式分别乘方再把所得的幂相乘,分别求出即可.
【解】:A.a2 a3=a5,故此选项正确;
B.a+a=2a,故此选项错误;
C.(a2)3=a6,故此选项错误;
D.a2(a+1)=a3+a2,故此选项错误;
故选:A.
3、计算:(x2+xy+y2)(x2-xy+y2)
【分析】若利用多项式的乘法法则展开,再合并同类项,比较麻烦,可以考虑变形,使其符合乘法公式。
【解】原式=[(x2+y2)+xy)][(x2+y2)-xy]=(x2+y2)2-(xy)2=x4+2x2y2+y4-x2y2==x4+x2y2+y4
4、已知2m=3,2n=4,则2m+n=________。
【分析】2m+n=2m.2n,再整体代入。
【解】2m+n=2m.2n=3×4=12
2、建立方程,破解参数
【例2】若(x2+nx+3)(x2-3x+m)的展开式中不含x2和x3的项,求m,n的值。
【分析】没有必要全部相乘,只需要考虑哪些项相乘得到含有x2的项,哪些项相乘,得到含有x3的项。
【解】展开后得到含有x2的项目是:mx2++3x2-3nx=(m-3n+3)x2
展开后得到含有x3的项是:-3x3+nx3=(n-3)x3
由题意,得:
【点评】解决一个问题有几种不同的方法,我们应该先考虑哪种方法简单些,有选择的使用。
【变式练习】
已知(3x2-2x+1)(x+b)中不含x2项,求b的值。
【解】展开后含有x2的项是:3bx2-2x2=(3b-2)x2,所以3b-2=0,b=
3、适当转化,柳暗花明又一村
【例3】计算:0.25201142012-86700.52011
【分析】逆用同底数幂的乘法法则,运算变得十分简单。
【点评】有时适当转化,使问题能逆用公式,复杂的问题,会变得简单。
【变式练习】
比较216×310与210×314
【解】216×310=26×210×310=26×610,210×314=210×310×34=610×34
26=64<34=81, ∴26×610<610×34, ∴216×310<210×314
4、运用整体思想,化繁为简
【例4】(贵州2010)已知x2-2x=1,求(x-1)(3x+1)-(x+1)2的值。
【分析】由条件无法求出x,可以先化简要求的式子,再整体代入。
【解】(x-1)(3x+1)-(x+1)2=3x2+x-3x-1-(x2+2x+1)
= 3x2+x-3x-1-x2-2x-1
=2x2-4x-2
=2(x2-2x)-2=2×1-2=0
【变式练习】已知a+b=17,ab=60,则(a-b)2=______,a2+b2=_________.
【解】(a-b)2=(a+b)2-4ab=172-4×60=289-240=49
a2+b2=(a+b)2-2ab=172-2××60=289-120=169
5、数形结合,变抽象为直观
【例5】(2011浙江衢州)有足够多的长方形和正方形卡片,如下图:
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.
这个长方形的代数意义是 a2+3ab+2b2=(a+b)(a+2b) .
(2)小明想用类似方法解释多项式乘法(a+3b)(2a+b)=2a2+7ab+3b2,那么需用2号卡片 3 张,3号卡片 7 张.
【分析】:(1)先根据题意画出图形,然后求出长方形的长和宽,长为a+2b,宽为a+b,从而求出长方形的面积;
(2)先求出1号、2号、3号图形的面积,然后由(a+3b)(2a+b)=2a2+7ab+3b2得出答案.
【解】:(1)
或
a2+3ab+2b2=(a+b)(a+2b),
故答案为a2+3ab+2b2=(a+b)(a+2b)
(2)1号正方形的面积为a2,2号正方形的面积为b2,3号长方形的面积为ab,
所以需用2号卡片3张,3号卡片7张,
故答案为3,7.
【点评】:本题主要考查了整式的混合运算,用到的知识点有长方形的面积公式和正方形的面积公式.
【变式练习】
(2011湖州,16,4分)如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长、宽边长分别是2和1的长方形.现有甲类纸片1张,乙类纸片4张,则应至少取丙类纸片 张才能用它们拼成一个新的正方形.
【分析】:根据构成的新正方形的面积一定是一个完全平方数,根据三张纸片的面积即可确定.
【解】:解:甲类纸片1张,乙类纸片4张,总面积是4+4=8,大于8的完全平方数依次是9,16,25…,而丙的面积是2,因而不可能;当总面积是16时,取的丙纸片的总面积是8,因而是4张.因而应至少取丙类纸片4张才能用它们拼成一个新的正方形.故答案为4.
【点评】:本题主要考查了完全平方公式的几何背景,正确理解新正方形的面积是完全平方数是解题的关键.
三、课堂练习
1 、先化简再求值:其中x=-2,y=-3,z=1.
2 、若n为正整数,且x2n=3求(x3n)2-4(x2)2n的值。
【解】(x3n)2-4(x2)2n
=x6n-4x4n
=(x2n)3 -4(x2n)2
=33 -4 × 32
=27-36
=-9
3 、计算:(-a2b)3+5(a2)2.(-b)3.a2+3b3a6
【解】原式=-a6b3+5a4.(-b3).a2+3b3a6=-a6b3-5a6b3+3a6b3=-3a6b3
4、(2011湖南衡阳)先化简,再求值.(x+1)2+x(x﹣2).其中.
【分析】:本题需先把要求的式子进行化简整理,再把x的值代入即可求出结果.
【解】:(x+1)2+x(x﹣2)
=x2+2x+1+x2﹣2x
=2x2+1
当时原式=2×+1=
四、反思小结
这节课你掌握了整式运算中哪些法则?
1、熟练掌握整式的加减法、乘法法则、乘法公式是解题的基础;2、适当训练,提高解题能力;3、注意总结经验,归纳解题技巧。
作业P 109 A 1、2、3 ,B 2,3
教学目标
1 掌握多项式的加减法、乘法运算法则,并能熟练地进行多项式的加减、乘运算。
2掌握同底数的幂的乘法、幂的乘方运算法则并能熟练的进行运算。
教学重点、难点
重点:整式加、减、乘运算法则及应用。
难点:多项式加、减、乘混合运算
教学过程
知识网络
二 知识要点
什么叫同类项?怎样合并同类项?
所含字母_____,且相同字母的指数也_______的项,叫同类项。同类项可以合并方法是:系数_________,字母和字母的指数_______.如:2a2b-3a2b=(2-3)a2b= -a2b
(2)多项式的加减法:合并同类项。
(3)同底数幂的乘法:同底数的幂相乘,底数不变指数相加。即:am.an=am+n(m,n是正整数)
(4)幂的乘方:底数不变,指数相乘。即:(am)n=amn.(m,n是正整数)
(5)单项式乘以单项式:系数乘以系数,同底数的幂相乘。如:2a2b.3ab2=6a3b3
(6)单项式乘以多项式:用单项式分别乘以多项式的每一项。即:a(b+c+d)=ab+ac+ad
(7)多项式乘以多项式:用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。即:(a+b)(c+d)=ac+ad+bc+bd
(8)乘法公式
①平方差公式:(a+b)(a-b)=a2-b2
两个数的和乘以这两个数的差,等于这两个数的平方差。
②(a±b)2=a2±2ab+b2
两个数的和或差的平方,等于这两个数的平方和加上(或减去)这两个数的积的二倍。
二 专题训练
1、把握公式特征,灵活运算法则
【例1】有这样一道题:“计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+2x2y-y3)
的值,其中x= ,y=-1.”错抄成了“x= ”,但他计算的结果也是正确的,这是怎么回事呢?
【分析】先化简,由于x的值抄错成它的相反数,所以,化简后的式子含有x的项中,只有x2,而没有x3、x项或者没有含有x的项。
【解】原式=2x3-3x2y-2xy2-x3+2xy2-y3-x3+2x2y-y3=-x2y-2y3
当x=0.5,y=-1时,原式=-0.52×(-1)-2×(-1)3=2.25
当x=-0.5,y=-1时,原式=-(-0.5)2×(-1)-2×(-1)3=2.25
【变式练习】
1、(2010福建泉州)若a、b 是正数,a﹣b=l,ab=2,则a+b=( )
A.﹣3 B.3 C.±3 D.9
【分析】根据(a+b)2=(a﹣b)2+4ab,代值计算,再开平方求解.注意若a、b 是正数,则a+b>0.
【解】:∵(a+b)2=(a﹣b)2+4ab=12+4×2=9,开平方,得a+b=±3,又∵a、b 是正数,
∴a+b>0,∴a+b=3.故选B.
【点评】本题考查了完全平方公式,熟记公式的几个变形公式对解题大有帮助.
2、(2011广东湛江)下列计算正确的是( )
A、a2 a3=a5 B、a+a=a2 C、(a2)3=a5 D、a2(a+1)=a3+1
【分析】:根据同底数幂的乘法法则:底数不变,指数相加,以及合并同类项:只把系数相加,字母及其指数完全不变.积的乘方:等于把积的每一个因式分别乘方再把所得的幂相乘,分别求出即可.
【解】:A.a2 a3=a5,故此选项正确;
B.a+a=2a,故此选项错误;
C.(a2)3=a6,故此选项错误;
D.a2(a+1)=a3+a2,故此选项错误;
故选:A.
3、计算:(x2+xy+y2)(x2-xy+y2)
【分析】若利用多项式的乘法法则展开,再合并同类项,比较麻烦,可以考虑变形,使其符合乘法公式。
【解】原式=[(x2+y2)+xy)][(x2+y2)-xy]=(x2+y2)2-(xy)2=x4+2x2y2+y4-x2y2==x4+x2y2+y4
4、已知2m=3,2n=4,则2m+n=________。
【分析】2m+n=2m.2n,再整体代入。
【解】2m+n=2m.2n=3×4=12
2、建立方程,破解参数
【例2】若(x2+nx+3)(x2-3x+m)的展开式中不含x2和x3的项,求m,n的值。
【分析】没有必要全部相乘,只需要考虑哪些项相乘得到含有x2的项,哪些项相乘,得到含有x3的项。
【解】展开后得到含有x2的项目是:mx2++3x2-3nx=(m-3n+3)x2
展开后得到含有x3的项是:-3x3+nx3=(n-3)x3
由题意,得:
【点评】解决一个问题有几种不同的方法,我们应该先考虑哪种方法简单些,有选择的使用。
【变式练习】
已知(3x2-2x+1)(x+b)中不含x2项,求b的值。
【解】展开后含有x2的项是:3bx2-2x2=(3b-2)x2,所以3b-2=0,b=
3、适当转化,柳暗花明又一村
【例3】计算:0.25201142012-86700.52011
【分析】逆用同底数幂的乘法法则,运算变得十分简单。
【点评】有时适当转化,使问题能逆用公式,复杂的问题,会变得简单。
【变式练习】
比较216×310与210×314
【解】216×310=26×210×310=26×610,210×314=210×310×34=610×34
26=64<34=81, ∴26×610<610×34, ∴216×310<210×314
4、运用整体思想,化繁为简
【例4】(贵州2010)已知x2-2x=1,求(x-1)(3x+1)-(x+1)2的值。
【分析】由条件无法求出x,可以先化简要求的式子,再整体代入。
【解】(x-1)(3x+1)-(x+1)2=3x2+x-3x-1-(x2+2x+1)
= 3x2+x-3x-1-x2-2x-1
=2x2-4x-2
=2(x2-2x)-2=2×1-2=0
【变式练习】已知a+b=17,ab=60,则(a-b)2=______,a2+b2=_________.
【解】(a-b)2=(a+b)2-4ab=172-4×60=289-240=49
a2+b2=(a+b)2-2ab=172-2××60=289-120=169
5、数形结合,变抽象为直观
【例5】(2011浙江衢州)有足够多的长方形和正方形卡片,如下图:
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.
这个长方形的代数意义是 a2+3ab+2b2=(a+b)(a+2b) .
(2)小明想用类似方法解释多项式乘法(a+3b)(2a+b)=2a2+7ab+3b2,那么需用2号卡片 3 张,3号卡片 7 张.
【分析】:(1)先根据题意画出图形,然后求出长方形的长和宽,长为a+2b,宽为a+b,从而求出长方形的面积;
(2)先求出1号、2号、3号图形的面积,然后由(a+3b)(2a+b)=2a2+7ab+3b2得出答案.
【解】:(1)
或
a2+3ab+2b2=(a+b)(a+2b),
故答案为a2+3ab+2b2=(a+b)(a+2b)
(2)1号正方形的面积为a2,2号正方形的面积为b2,3号长方形的面积为ab,
所以需用2号卡片3张,3号卡片7张,
故答案为3,7.
【点评】:本题主要考查了整式的混合运算,用到的知识点有长方形的面积公式和正方形的面积公式.
【变式练习】
(2011湖州,16,4分)如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长、宽边长分别是2和1的长方形.现有甲类纸片1张,乙类纸片4张,则应至少取丙类纸片 张才能用它们拼成一个新的正方形.
【分析】:根据构成的新正方形的面积一定是一个完全平方数,根据三张纸片的面积即可确定.
【解】:解:甲类纸片1张,乙类纸片4张,总面积是4+4=8,大于8的完全平方数依次是9,16,25…,而丙的面积是2,因而不可能;当总面积是16时,取的丙纸片的总面积是8,因而是4张.因而应至少取丙类纸片4张才能用它们拼成一个新的正方形.故答案为4.
【点评】:本题主要考查了完全平方公式的几何背景,正确理解新正方形的面积是完全平方数是解题的关键.
三、课堂练习
1 、先化简再求值:其中x=-2,y=-3,z=1.
2 、若n为正整数,且x2n=3求(x3n)2-4(x2)2n的值。
【解】(x3n)2-4(x2)2n
=x6n-4x4n
=(x2n)3 -4(x2n)2
=33 -4 × 32
=27-36
=-9
3 、计算:(-a2b)3+5(a2)2.(-b)3.a2+3b3a6
【解】原式=-a6b3+5a4.(-b3).a2+3b3a6=-a6b3-5a6b3+3a6b3=-3a6b3
4、(2011湖南衡阳)先化简,再求值.(x+1)2+x(x﹣2).其中.
【分析】:本题需先把要求的式子进行化简整理,再把x的值代入即可求出结果.
【解】:(x+1)2+x(x﹣2)
=x2+2x+1+x2﹣2x
=2x2+1
当时原式=2×+1=
四、反思小结
这节课你掌握了整式运算中哪些法则?
1、熟练掌握整式的加减法、乘法法则、乘法公式是解题的基础;2、适当训练,提高解题能力;3、注意总结经验,归纳解题技巧。
作业P 109 A 1、2、3 ,B 2,3
